On limiting behavior of ordinary and conditional first-passage times for a class of birth-death processes

Abstract

Let N(t) be a birth-death process on 𝒩= {0, 1, 2, ·· ·} governed by the transition rates λ_n > 0 (n ≧ 0) and μ_n > 0 (n ≧ 1) where λ_n → λ > 0 and μ_n → μ > 0 as n → ∞ and ρ = λ/μ. Let T_mn be the first-passage time of N(t) from m to n and define 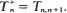It is shown that, when 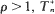converges in distribution to T_BP(μ,λ) as n → ∞ where T_{ΒΡ (μ,λ)} is the server busy period of an M/M/1 queueing system with arrival rate μ and service rate λ. Correspondingly T_0n/E[T_0n] converges to 1 with probability 1 as n →∞. Of related interest is the conditional first-passage time ^mT_rn of N(t) from r to n given no visit to m where m < r < n. As we shall see, the conditional first-passage time of N(t) can be viewed as an ordinary first-passage time of a modified birth-death process M(t) governed by 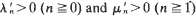where 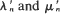are generated from λ_n and μ_n. Furthermore it is shown that for 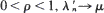and 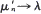while for 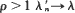and 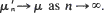This enables one to establish the relation between the limiting behavior of the ordinary first-passage times and that of the conditional first-passage times.