Cognitive diagnostic models (CDMs) are discrete latent variable models popular in educational and psychological measurement. In this work, motivated by the advantages of deep generative modeling and by identifiability considerations, we propose a new family of DeepCDMs, to hunt for deep discrete diagnostic information. The new class of models enjoys nice properties of identifiability, parsimony, and interpretability. Mathematically, DeepCDMs are entirely identifiable, including even fully exploratory settings and allowing to uniquely identify the parameters and discrete loading structures (the “\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\textbf{Q}$$\end{document}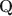 -matrices”) at all different depths in the generative model. Statistically, DeepCDMs are parsimonious, because they can use a relatively small number of parameters to expressively model data thanks to the depth. Practically, DeepCDMs are interpretable, because the shrinking-ladder-shaped deep architecture can capture cognitive concepts and provide multi-granularity skill diagnoses from coarse to fine grained and from high level to detailed. For identifiability, we establish transparent identifiability conditions for various DeepCDMs. Our conditions impose intuitive constraints on the structures of the multiple \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\textbf{Q}$$\end{document}
-matrices”) at all different depths in the generative model. Statistically, DeepCDMs are parsimonious, because they can use a relatively small number of parameters to expressively model data thanks to the depth. Practically, DeepCDMs are interpretable, because the shrinking-ladder-shaped deep architecture can capture cognitive concepts and provide multi-granularity skill diagnoses from coarse to fine grained and from high level to detailed. For identifiability, we establish transparent identifiability conditions for various DeepCDMs. Our conditions impose intuitive constraints on the structures of the multiple \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\textbf{Q}$$\end{document}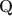 -matrices and inspire a generative graph with increasingly smaller latent layers when going deeper. For estimation and computation, we focus on the confirmatory setting with known \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\textbf{Q}$$\end{document}
-matrices and inspire a generative graph with increasingly smaller latent layers when going deeper. For estimation and computation, we focus on the confirmatory setting with known \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\textbf{Q}$$\end{document}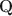 -matrices and develop Bayesian formulations and efficient Gibbs sampling algorithms. Simulation studies and an application to the TIMSS 2019 math assessment data demonstrate the usefulness of the proposed methodology.
-matrices and develop Bayesian formulations and efficient Gibbs sampling algorithms. Simulation studies and an application to the TIMSS 2019 math assessment data demonstrate the usefulness of the proposed methodology.