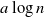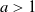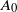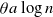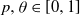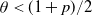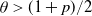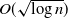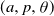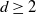Following Bradonjić and Saniee, we study a model of bootstrap percolation on the Gilbert random geometric graph on the 2-dimensional torus. In this model, the expected number of vertices of the graph is n, and the expected degree of a vertex is 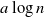$a\log n$ for some fixed 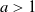$a>1$. Each vertex is added with probability p to a set 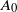$A_0$ of initially infected vertices. Vertices subsequently become infected if they have at least 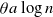$ \theta a \log n $ infected neighbours. Here 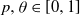$p, \theta \in [0,1]$ are taken to be fixed constants.

We show that if 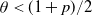$\theta < (1+p)/2$, then a sufficiently large local outbreak leads with high probability to the infection spreading globally, with all but o(n) vertices eventually becoming infected. On the other hand, for 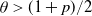$ \theta > (1+p)/2$, even if one adversarially infects every vertex inside a ball of radius 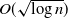$O(\sqrt{\log n} )$, with high probability the infection will spread to only o(n) vertices beyond those that were initially infected.

In addition we give some bounds on the 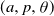$(a, p, \theta)$ regions ensuring the emergence of large local outbreaks or the existence of islands of vertices that never become infected. We also give a complete picture of the (surprisingly complex) behaviour of the analogous 1-dimensional bootstrap percolation model on the circle. Finally we raise a number of problems, and in particular make a conjecture on an ‘almost no percolation or almost full percolation’ dichotomy which may be of independent interest.

The hyperbolic random geometric graph was introduced by Krioukov et al. (Phys. Rev. E82, 2010). Among many equivalent models for the hyperbolic space, we study the d-dimensional Poincaré ball ( $d\ge 2$ ), with a general connectivity radius. While many phase transitions are known for the expectation asymptotics of certain subgraph counts, very little is known about the second-order results. Two of the distinguishing characteristics of geometric graphs on the hyperbolic space are the presence of tree-like hierarchical structures and the power-law behaviour of the degree distribution. We aim to reveal such characteristics in detail by investigating the behaviour of sub-tree counts. We show multiple phase transitions for expectation and variance in the resulting hyperbolic geometric graph. In particular, the expectation and variance of the sub-tree counts exhibit an intricate dependence on the degree sequence of the tree under consideration. Additionally, unlike the thermodynamic regime of the Euclidean random geometric graph, the expectation and variance may exhibit different growth rates, which is indicative of power-law behaviour. Finally, we also prove a normal approximation for sub-tree counts using the Malliavin–Stein method of Last et al. (Prob. Theory Relat. Fields165, 2016), along with the Palm calculus for Poisson point processes.

We make the first steps towards generalising the theory of stochastic block models, in the sparse regime, towards a model where the discrete community structure is replaced by an underlying geometry. We consider a geometric random graph over a homogeneous metric space where the probability of two vertices to be connected is an arbitrary function of the distance. We give sufficient conditions under which the locations can be recovered (up to an isomorphism of the space) in the sparse regime. Moreover, we define a geometric counterpart of the model of flow of information on trees, due to Mossel and Peres, in which one considers a branching random walk on a sphere and the goal is to recover the location of the root based on the locations of leaves. We give some sufficient conditions for percolation and for non-percolation of information in this model.