We lay the groundwork in this first installment of a series of papers aimed at developing a theory of Hrushovski–Kazhdan style motivic integration for certain types of nonarchimedean $o$-minimal fields, namely power-bounded $T$-convex valued fields, and closely related structures. The main result of the present paper is a canonical homomorphism between the Grothendieck semirings of certain categories of definable sets that are associated with the $\text{VF}$-sort and the $\text{RV}$-sort of the language ${\mathcal{L}}_{T\text{RV}}$. Many aspects of this homomorphism can be described explicitly. Since these categories do not carry volume forms, the formal groupification of the said homomorphism is understood as a universal additive invariant or a generalized Euler characteristic. It admits not just one, but two specializations to $\unicode[STIX]{x2124}$. The overall structure of the construction is modeled on that of the original Hrushovski–Kazhdan construction.

Let T be a complete o-minimal extension of the theory of real closed fields. We characterize the convex hulls of elementary substructures of models of T and show that the residue field of such a convex hull has a natural expansion to a model of T. We give a quantifier elimination relative to T for the theory of pairs (ℛ, V) where ℛ ⊨ T and V ≠ ℛ is the convex hull of an elementary substructure of ℛ. We deduce that the theory of such pairs is complete and weakly o-minimal. 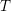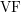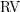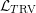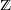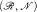We also give a quantifier elimination relative to T for the theory of pairs with ℛ a model of 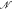T and a proper elementary substructure that is Dedekind complete in ℛ. We deduce that the theory of such “tame” pairs is complete.