Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T09:37:41.240Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Euler characteristic in power-bounded T-convex valued fields

Part of: Birational geometry Topological fields Model theory

Published online by Cambridge University Press:  14 September 2017

Yimu Yin
Yimu Yin*
Affiliation:
Department of Philosophy, Sun Yat-Sen University, 135 Xingang Road West, Guangzhou 510275, China email yimu.yin@hotmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We lay the groundwork in this first installment of a series of papers aimed at developing a theory of Hrushovski–Kazhdan style motivic integration for certain types of nonarchimedean $o$-minimal fields, namely power-bounded 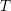$T$-convex valued fields, and closely related structures. The main result of the present paper is a canonical homomorphism between the Grothendieck semirings of certain categories of definable sets that are associated with the 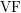$\text{VF}$-sort and the 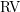$\text{RV}$-sort of the language 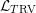${\mathcal{L}}_{T\text{RV}}$. Many aspects of this homomorphism can be described explicitly. Since these categories do not carry volume forms, the formal groupification of the said homomorphism is understood as a universal additive invariant or a generalized Euler characteristic. It admits not just one, but two specializations to 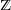$\unicode[STIX]{x2124}$. The overall structure of the construction is modeled on that of the original Hrushovski–Kazhdan construction.

Keywords

motivic integrationEuler characteristico-minimal valued fieldT-convexity

MSC classification

Primary: 12J25: Non-Archimedean valued fields 03C64: Model theory of ordered structures; o-minimality 14E18: Arcs and motivic integration 03C98: Applications of model theory
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 12 , December 2017 , pp. 2591 - 2642
Copyright
© The Author 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cluckers, R. and Loeser, F., Constructible motivic functions and motivic integration , Invent. Math. 173 (2008), 23–121.CrossRefGoogle Scholar
van den Dries, L., T-convexity and tame extensions II , J. Symbolic Logic 62 (1997), 14–34.CrossRefGoogle Scholar
van den Dries, L., Tame topology and o-minimal structures, London Mathematical Society Lecture Note Series, vol. 248 (Cambridge University Press, Cambridge, 1998).Google Scholar
van den Dries, L. and Lewenberg, A. H., T-convexity and tame extensions , J. Symbolic Logic 60 (1995), 74–102.Google Scholar
van den Dries, L., Macintyre, A. and Marker, D., The elementary theory of restricted analytic fields with exponentiation , Ann. of Math. (2) 140 (1994), 183–205.Google Scholar
van den Dries, L. and Miller, C., Geometric categories and o-minimal structures , Duke Math. J. 84 (1996), 497–540.Google Scholar
van den Dries, L. and Speissegger, P., The field of reals with multisummable series and the exponential function , Proc. Lond. Math. Soc. (3) 81 (2000), 513–565.Google Scholar
Halupczok, I. and Yin, Y., Lipschitz stratification in power-bounded o-minimal fields , J. Eur. Math. Soc. (JEMS) (2015), to appear.Google Scholar
Holly, J., Canonical forms for definable subsets of algebraically closed and real closed valued fields , J. Symbolic Logic 60 (1995), 843–860.Google Scholar
Hrushovski, E. and Kazhdan, D., Integration in valued fields, Algebraic Geometry and Number Theory, Progr. Math., vol. 253 (Birkhäuser, Boston, 2006), 261–405.Google Scholar
Hrushovski, E. and Loeser, F., Monodromy and the Lefschetz fixed point formula , Ann. Sci. Éc. Norm. Supér. (4) 48 (2015), 313–349.Google Scholar
Kageyama, M. and Fujita, M., Grothendieck rings of o-minimal expansions of ordered abelian groups , J. Algebra 299 (2006), 8–20.CrossRefGoogle Scholar
Macpherson, D., Marker, D. and Steinhorn, C., Weakly o-minimal structures and real closed fields , Trans. Amer. Math. Soc. 352 (2000), 5435–5483.Google Scholar
Maříková, J., o-minimal residue fields of o-minimal fields , Ann. Pure Appl. Logic 162 (2011), 457–464.Google Scholar
McCrory, C. and Parusiński, A., Virtual Betti numbers of real algebraic varieties , C. R. Math. Acad. Sci. Paris I 336 (2003), 763–768.Google Scholar
Peterzil, Y. and Starchenko, S., Computing o-minimal topological invariants using differential topology , Trans. Amer. Math. Soc. 359 (2007), 1375–1401.Google Scholar
Tyne, J., $T$ -levels and $T$ -convexity, PhD thesis, University of Illinois at Urbana-Champaign (2003).Google Scholar
Yin, Y., Quantifier elimination and minimality conditions in algebraically closed valued fields, Preprint (2009), arXiv:1006.1393v1.Google Scholar
Yin, Y., Special transformations in algebraically closed valued fields , Ann. Pure Appl. Logic 161 (2010), 1541–1564.Google Scholar
Yin, Y., Integration in algebraically closed valued fields , Ann. Pure Appl. Logic 162 (2011), 384–408.Google Scholar
Yin, Y., Additive invariants in $o$ -minimal valued fields, Preprint (2013), arXiv:1307.0224.Google Scholar
Yin, Y., Integration in algebraically closed valued fields with sections , Ann. Pure Appl. Logic 164 (2013), 1–29.Google Scholar