Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lewenberg, Adam
1996.
Locally injective maps in o-minimal structures without poles are surjective.
Proceedings of the American Mathematical Society,
Vol. 124,
Issue. 9,
p.
2839.
Tressl, Marcus
2005.
The elementary theory of Dedekind cuts in polynomially bounded structures.
Annals of Pure and Applied Logic,
Vol. 135,
Issue. 1-3,
p.
113.
Tressl, Marcus
2006.
Pseudo completions and completions in stages of o-minimal structures.
Archive for Mathematical Logic,
Vol. 45,
Issue. 8,
p.
983.
Dolich, Alfred
2007.
A Note on Weakly O-Minimal Structures and Definable Completeness.
Notre Dame Journal of Formal Logic,
Vol. 48,
Issue. 2,
Dolich, Alfred
Miller, Chris
and
Steinhorn, Charles
2009.
Structures having o-minimal open core.
Transactions of the American Mathematical Society,
Vol. 362,
Issue. 3,
p.
1371.
Maříková, Jana
2011.
O-minimal residue fields of o-minimal fields.
Annals of Pure and Applied Logic,
Vol. 162,
Issue. 6,
p.
457.
Miller, Chris
2012.
Lecture Notes on O-Minimal Structures and Real Analytic Geometry.
Vol. 62,
Issue. ,
p.
43.
Aschenbrenner, Matthias
van den Dries, Lou
and
van der Hoeven, Joris
2013.
Toward a Model Theory for Transseries.
Notre Dame Journal of Formal Logic,
Vol. 54,
Issue. 3-4,
Aschenbrenner, Matthias
and
Goldbring, Isaac
2014.
Transseries and Todorov–Vernaeve’s asymptotic fields.
Archive for Mathematical Logic,
Vol. 53,
Issue. 1-2,
p.
65.
Ramakrishnan, Janak
2014.
Definable functions continuous on curves in o-minimal structures.
Annals of Pure and Applied Logic,
Vol. 165,
Issue. 7-8,
p.
1339.
Phillips, Laura R.
2015.
Positive primitive formulae of modules over rings of semi-algebraic functions on a curve.
Archive for Mathematical Logic,
Vol. 54,
Issue. 5-6,
p.
587.
Laskowski, Michael C.
and
Shaw, Christopher S.
2016.
Definable choice for a class of weakly o-minimal theories.
Archive for Mathematical Logic,
Vol. 55,
Issue. 5-6,
p.
735.
Hong, Jizhan
2016.
Separably closed valued fields: Immediate expansions.
Israel Journal of Mathematics,
Vol. 216,
Issue. 2,
p.
811.
Yin, Yimu
2017.
Generalized Euler characteristic in power-bounded T-convex valued fields.
Compositio Mathematica,
Vol. 153,
Issue. 12,
p.
2591.
García Ramírez, Erick
2017.
Non‐archimedean stratifications of tangent cones.
Mathematical Logic Quarterly,
Vol. 63,
Issue. 3-4,
p.
299.
Ealy, Clifton
Haskell, Deirdre
and
Maříková, Jana
2019.
Residue Field Domination in Real Closed Valued Fields.
Notre Dame Journal of Formal Logic,
Vol. 60,
Issue. 3,
García Ramírez, Erick
2020.
Definable Functions and Stratifications in Power-Bounded T -Convex Fields.
Notre Dame Journal of Formal Logic,
Vol. 61,
Issue. 3,
Cubides Kovacsics, Pablo
and
Haskell, Deirdre
2020.
Real closed valued fields with analytic structure.
Proceedings of the Edinburgh Mathematical Society,
Vol. 63,
Issue. 1,
p.
249.
Andújar Guerrero, Pablo
Thomas, Margaret E. M.
and
Walsberg, Erik
2021.
Directed sets and topological spaces definable in o‐minimal structures.
Journal of the London Mathematical Society,
Vol. 104,
Issue. 3,
p.
989.
Fornasiero, Antongiulio
and
Kaplan, Elliot
2021.
Generic derivations on o-minimal structures.
Journal of Mathematical Logic,
Vol. 21,
Issue. 02,
p.
2150007.
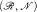 with ℛ a model of T and
with ℛ a model of T and 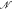 a proper elementary substructure that is Dedekind complete in ℛ. We deduce that the theory of such “tame” pairs is complete.
a proper elementary substructure that is Dedekind complete in ℛ. We deduce that the theory of such “tame” pairs is complete.
