Let  $\mathfrak{A}$ be a
$\mathfrak{A}$ be a  ${{C}^{*}}$-algebra with real rank zero that has the stable weak cancellation property. Let
${{C}^{*}}$-algebra with real rank zero that has the stable weak cancellation property. Let  $\Im $ be an ideal of
$\Im $ be an ideal of  $\mathfrak{A}$ such that
$\mathfrak{A}$ such that  $\Im $ is stable and satisfies the corona factorization property. We prove that
$\Im $ is stable and satisfies the corona factorization property. We prove that
 $$0\,\to \,\Im \,\to \mathfrak{A}\,\to \,\mathfrak{A}/\Im \,\to \,0$$
$$0\,\to \,\Im \,\to \mathfrak{A}\,\to \,\mathfrak{A}/\Im \,\to \,0$$
is a full extension if and only if the extension is stenotic and  $K$-lexicographic. As an immediate application, we extend the classification result for graph
$K$-lexicographic. As an immediate application, we extend the classification result for graph  ${{C}^{*}}$-algebras obtained by Tomforde and the first named author to the general non-unital case. In combination with recent results by Katsura, Tomforde, West, and the first named author, our result may also be used to give a purely
${{C}^{*}}$-algebras obtained by Tomforde and the first named author to the general non-unital case. In combination with recent results by Katsura, Tomforde, West, and the first named author, our result may also be used to give a purely  $K$-theoretical description of when an essential extension of two simple and stable graph
$K$-theoretical description of when an essential extension of two simple and stable graph  ${{C}^{*}}$-algebras is again a graph
${{C}^{*}}$-algebras is again a graph  ${{C}^{*}}$-
algebra.
${{C}^{*}}$-
algebra.
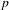 $p$-ADIQUES ET MODULO
$p$-ADIQUES ET MODULO 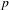 $p$ DE
$p$ DE 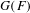 $G(F)$
$G(F)$