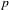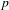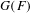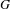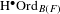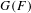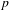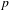Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Breuil, Christophe
2015.
Induction parabolique et (φ,Γ)-modules.
Algebra & Number Theory,
Vol. 9,
Issue. 10,
p.
2241.
Hauseux, Julien
2018.
On the exactness of ordinary parts over a local field of characteristic p.
Pacific Journal of Mathematics,
Vol. 295,
Issue. 1,
p.
17.
Hauseux, Julien
Schmidt, Tobias
and
Sorensen, Claus
2018.
Deformation rings and parabolic induction.
Journal de théorie des nombres de Bordeaux,
Vol. 30,
Issue. 2,
p.
695.
Hauseux, Julien
2018.
Parabolic induction and extensions.
Algebra & Number Theory,
Vol. 12,
Issue. 4,
p.
779.
Hauseux, Julien
2019.
Sur une conjecture de Breuil–Herzig.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2019,
Issue. 751,
p.
91.
Colmez, Pierre
Dospinescu, Gabriel
Hauseux, Julien
and
Nizioł, Wiesława
2021.
p-adic étale cohomology of period domains.
Mathematische Annalen,
Vol. 381,
Issue. 1-2,
p.
105.
Gehrmann, Lennart
2021.
Automorphic ℒ‐invariants for reductive groups.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2021,
Issue. 779,
p.
57.
Colmez, Pierre
Dospinescu, Gabriel
and
Nizioł, Wiesława
2023.
Factorisation de la cohomologie étale p-adique de la tour de Drinfeld.
Forum of Mathematics, Pi,
Vol. 11,
Issue. ,
Abe, Noriyuki
2023.
EXTENSION BETWEEN SIMPLE MODULES OF PRO-p-IWAHORI HECKE ALGEBRAS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 22,
Issue. 6,
p.
2775.
Heyer, Claudius
2023.
The left adjoint of derived parabolic induction.
Mathematische Zeitschrift,
Vol. 305,
Issue. 3,
Breuil, Christophe
and
Ding, Yiwen
2023.
Sur un problème de compatibilité local-global localement analytique.
Memoirs of the American Mathematical Society,
Vol. 290,
Issue. 1442,