We study combinatorial and order theoretic structures arising from the fragment of combinatory logic spanned by the basic combinator ${{\mathbf{M}}}$ . This basic combinator, named as the Mockingbird by Smullyan, is defined by the rewrite rule ${{\mathbf{M}}} \mathsf{x}_1 \to \mathsf{x}_1 \mathsf{x}_1$ . We prove that the reflexive and transitive closure of this rewrite relation is a partial order on terms on ${{\mathbf{M}}}$ and that all connected components of its rewrite graph are Hasse diagram of lattices. This last result is based on the introduction of new lattices on duplicative forests, which are sorts of treelike structures. These lattices are not graded, not self-dual, and not semi-distributive. We present some enumerative properties of these lattices like the enumeration of their elements, of the edges of their Hasse diagrams, and of their intervals. These results are derived from formal power series on terms and on duplicative forests endowed with particular operations.

Wick polynomials and Wick products are studied in the context of noncommutative probability theory. It is shown that free, Boolean, and conditionally free Wick polynomials can be defined and related through the action of the group of characters over a particular Hopf algebra. These results generalize our previous developments of a Hopf-algebraic approach to cumulants and Wick products in classical probability theory.

In this paper a determinant identity is established, from which a simple proof of the multivariate Lagrange–Good inversion formula follows directly. Further discussion on a discrete analogue of the Lagrange–Good inversion formula is also presented.

The Chowla conjecture states that if $t$ is any given positive integer, there are infinitely many prime positive integers 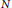$N$ such that 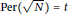$\text{Per}\left( \sqrt{N} \right)\,=\,t$, where 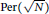$\text{Per}\left( \sqrt{N} \right)$ is the period length of the continued fraction expansion for 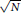$\sqrt{N}$. C. Friesen proved that, for any 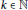$k\,\in \,\mathbb{N}$, there are infinitely many square-free integers 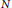$N$, where the continued fraction expansion of 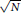$\sqrt{N}$ has a fixed period. In this paper, we describe all polynomials 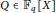$Q\,\in \,{{\mathbb{F}}_{q}}\left[ X \right]$ for which the continued fraction expansion of $\sqrt{Q}$ has a fixed period. We also give a lower bound of the number of monic, non-squares polynomials 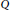$Q$ such that 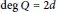$\deg \,Q=\,2d$ and 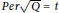$Per\sqrt{Q}\,=\,t$.

In this paper, we study rational approximations for certain algebraic power series over a finite field. We obtain results for irrational elements of strictly positive degree satisfying an equation of the type

$$\alpha =\frac{A{{\alpha }^{q}}+B}{C{{\alpha }^{q}}},$$

where $\left( A,B,C \right)\,\in \,{{\left( {{\mathbb{F}}_{q}}\left[ X \right] \right)}^{2}}\times \mathbb{F}_{q}^{*}\left[ X \right]$. In particular, under some conditions on the polynomials $A,\,B$ and $C$, we will give well approximated elements satisfying this equation.

LetLϕ,λ = {ω ∈ Σ∗| ϕ(ω) > λ} be thelanguage recognized by a formal seriesϕ:Σ∗ → ℝ with isolated cut pointλ. We provide new conditions that guarantee the regularity of thelanguage Lϕ,λ in the case thatϕ is rational or ϕ is a Hadamard quotient of rationalseries. Moreover the decidability property of such conditions is investigated.

In this paper we extend the computation of the the typical curves of algebraic K-theory done by Lars Hesselholt and Ib Madsen to general tensor algebras. The models used allow us to determine the stages of the Taylor tower of algebraic K-theory as a functor of augmented algebras, as defined by Tom Goodwillie, when evaluated on derived tensor algebras.

For R a discrete ring, and M a simplicial R-bimodule, we let R(M) denote the (derived) tensor algebra of M over R, and πR denote the ring of formal (derived) power series in M over R. We define a natural transformation of functors of simplicial R-bimodules Φ: which is closely related to Waldhausen's equivalence We show that Φ induces an equivalence on any finite stage of Goodwillie's Taylor towers of the functors at any simplicial bimodule. This is used to show that there is an equivalence of functors , and for connected bimodules, also an equivalence

Let R be a domain contained in a rank-1 valuation ring of its quotient field. Let R⟦X⟧ be the ring of formal power series over R, and let F be the quotient field of R⟦X⟧. We prove that F is Hilbertian. This resolves and generalizes an open problem of Jarden, and allows to generalize previous Galois-theoretic results over fields of power series.

The paper represents the first part of a series ofpapers on realization theory of switched systems. Part I presents realization theory of linear switched systems,Part II presents realization theory of bilinear switched systems.More precisely, in Part I necessary and sufficient conditionsare formulated for a family of input-output maps to berealizable by a linear switched system and a characterizationof minimal realizations is presented. The paper treats two types of switched systems.The first one is when all switching sequences are allowed. The second one is when only a subset of switching sequences isadmissible, but within this restricted set the switching times are arbitrary.The paper uses the theory of formal power series to derivethe results on realization theory.

This paper is the second part of a series of papers dealing withrealization theory of switched systems.The current Part II addresses realization theory of bilinear switchedsystems. In Part I [Petreczky, ESAIM: COCV, DOI: 10.1051/cocv/2010014] we presented realizationtheory of linear switched systems.More precisely, in Part II we present necessary and sufficient conditionsfor a family of input-output maps to berealizable by a bilinear switched system, together with a characterizationof minimal realizations.Similarly to Part I, the paper deals with two types of switched systems.The first one is when all switching sequences are allowed. The second one is when only a subset of switching sequences isadmissible, but within this restricted set the switching times are arbitrary.The paper uses the theory of formal power series to derivethe results on realization theory.

Parikh matrices have become a useful tool for investigation of subword structure of words. Several generalizations of this concept have been considered. Based on the concept of formal power series, we describe a general framework covering most of these generalizations. In addition, we provide a new characterization of binary amiable words – words having a common Parikh matrix.

A Bernstein–Walsh type inequality for ${{C}^{\infty }}$ functions of several variables is derived, which then is applied to obtain analogs and generalizations of the following classical theorems: (1) Bochnak– Siciak theorem: a ${{C}^{\infty }}$ function on ${{\mathbb{R}}^{n}}$ that is real analytic on every line is real analytic; (2) Zorn–Lelong theorem: if a double power series $F\left( x,y \right)$ converges on a set of lines of positive capacity then $F\left( x,y \right)$ is convergent; (3) Abhyankar–Moh–Sathaye theorem: the transfinite diameter of the convergence set of a divergent series is zero.