Vanishing cycles, introduced over half a century ago, are a fundamental tool for studying the topology of complex hypersurface singularity germs, as well as the change in topology of a degenerating family of projective manifolds. More recently, vanishing cycles have found deep applications in enumerative geometry, representation theory, applied algebraic geometry, birational geometry, etc. In this survey, we introduce vanishing cycles from a topological perspective and discuss some of their applications.
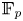 $\mathbb {F}_p$-sheaves
$\mathbb {F}_p$-sheaves
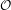 ${\mathcal{O}}$
${\mathcal{O}}$