Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T17:16:54.323Z Has data issue: false hasContentIssue false
  • English
  • Français

Parabolic category O, perverse sheaves on Grassmannians, Springer fibres and Khovanov homology

Part of: Rings and algebras arising under various constructions Lie algebras and Lie superalgebras Low-dimensional topology Representation theory of groups Linear algebraic groups and related topics Special varieties

Published online by Cambridge University Press:  01 July 2009

Catharina Stroppel
Catharina Stroppel*
Affiliation:
Department of Mathematics, University of Glasgow, University Gardens, Glasgow G12 8QW, UK (email: c.stroppel@maths.gla.ac.uk)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

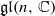For a fixed parabolic subalgebra 𝔭 of we prove that the centre of the principal block 𝒪0𝔭 of the parabolic category 𝒪 is naturally isomorphic to the cohomology ring H*(ℬ𝔭) of the corresponding Springer fibre. We give a diagrammatic description of 𝒪0𝔭 for maximal parabolic 𝔭 and give an explicit isomorphism to Braden’s description of the category PervB(G(k,n)) of Schubert-constructible perverse sheaves on Grassmannians. As a consequence Khovanov’s algebra ℋn is realised as the endomorphism ring of some object from PervB(G(n,n)) which corresponds under localisation and the Riemann–Hilbert correspondence to a full projective–injective module in the corresponding category 𝒪0𝔭. From there one can deduce that Khovanov’s tangle invariants are obtained from the more general functorial invariants in [C. Stroppel, Categorification of the Temperley Lieb category, tangles, and cobordisms via projective functors, Duke Math. J. 126(3) (2005), 547–596] by restriction.

Keywords

Khovanov homologySpringer fibreknot invariantsperverse sheavesKazhdan–Lusztig

MSC classification

Secondary: 16S99: None of the above, but in this section 17B10: Representations, algebraic theory (weights) 14M15: Grassmannians, Schubert varieties, flag manifolds 57M27: Invariants of knots and 3-manifolds 20C30: Representations of finite symmetric groups 20G05: Representation theory 14M17: Homogeneous spaces and generalizations
Type
Research Article
Information
Compositio Mathematica , Volume 145 , Issue 4 , July 2009 , pp. 954 - 992
Copyright
Copyright © Foundation Compositio Mathematica 2009

References

[1]Andersen, H. H. and Lauritzen, N., Twisted Verma modules, in Studies in Memory of Issai Schur, Progress in Mathematics, vol. 210 (Birkhäuser, Basel, 2003), 1–26.Google Scholar
[2]Andersen, H. H. and Stroppel, C., Twisting functors on 𝒪, Represent. Theory 7 (2003), 681–699.CrossRefGoogle Scholar
[3]Beilinson, A., Ginzburg, V. and Soergel, W., Koszul duality patterns in representation theory, J. Amer. Math. Soc. 9 (1996), 473–527.CrossRefGoogle Scholar
[4]Bernstein, J., Frenkel, I. and Khovanov, M., A categorification of the Temperley–Lieb algebra and Schur quotients of via projective and Zuckerman functors, Selecta Math. (N.S.) 5 (1999), 199–241.CrossRefGoogle Scholar
[5]Bernstein, J. N. and Gel’fand, S. I., Tensor products of finite- and infinite-dimensional representations of semisimple Lie algebras, Compositio Math. 41 (1980), 245–285.Google Scholar
[6]Bernstein, I. N., Gel’fand, I. M. and Gel’fand, S. I., A certain category of 𝔤-modules, Funkcional. Anal. i Priložen. 10 (1976), 1–8.Google Scholar
[7]Billey, S. C. and Warrington, G. S., Kazhdan–Lusztig polynomials for 321-hexagon-avoiding permutations, J. Algebraic Combin. 13 (2001), 111–136.CrossRefGoogle Scholar
[8]Braden, T., Perverse sheaves on Grassmannians, Canad. J. Math. 54 (2002), 493–532.CrossRefGoogle Scholar
[9]Brenti, F., Kazhdan–Lusztig and R-polynomials, Young’s lattice, and Dyck partitions, Pacific J. Math. 207 (2002), 257–286.CrossRefGoogle Scholar
[10]Brundan, J., Centers of degenerate cyclotomic Hecke algebras and parabolic category 𝒪, Preprint (2006), math.RT/0607717.Google Scholar
[11]Brundan, J., Symmetric functions, parabolic category 𝒪 and the Springer fiber, Duke Math. J. 143 (2008), 41–79, math.RT0608235.CrossRefGoogle Scholar
[12]De Concini, C. and Procesi, C., Symmetric functions, conjugacy classes and the flag variety, Invent. Math. 64 (1981), 203–219.CrossRefGoogle Scholar
[13]Fiebig, P., Centers and translation functors for the category 𝒪 over Kac–Moody algebras, Math. Z. 243 (2003), 689–717.CrossRefGoogle Scholar
[14]Fulton, W., Intersection theory, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), vol. 2 2nd edition (Springer, Berlin, 1998).CrossRefGoogle Scholar
[15]Fung, F., On the topology of components of some Springer fibers and their relation to Kazhdan–Lusztig theory, Adv. Math. 178 (2003), 244–276.CrossRefGoogle Scholar
[16]Garcia, A. M. and Procesi, C., On certain graded S n modules and q-Kostka polynomials, Adv. Math 94 (1992), 83–138.Google Scholar
[17]Gordon, I., Baby Verma modules for rational Cherednik algebras, Bull. London Math. Soc. 35 (2003), 321–336.CrossRefGoogle Scholar
[18]Hotta, R. and Shimomura, N., The fixed-point subvarieties of unipotent transformations on generalized flag varieties and the Green functions, Math. Ann. 241 (1979), 193–208.CrossRefGoogle Scholar
[19]Hotta, R. and Springer, T. A., A specialization theorem for certain Weyl group representations and an application to the Green polynomials of unitary groups, Invent. Math. 41 (1977), 113–127.CrossRefGoogle Scholar
[20]Hotta, R., Takeuchi, K. and Tanisaki, T., D-modules, perverse sheaves, and representation theory, Progress in Mathematics, vol. 236 (Birkhäuser, Basel, 2008), Translated from the 1995 Japanese edition by Takeuchi.CrossRefGoogle Scholar
[21]Irving, R., Projective modules in the category 𝒪S: self-duality, Trans. Amer. Math. Soc. 291 (1985), 701–732.Google Scholar
[22]Irving, R. S. and Shelton, B., Loewy series and simple projective modules in the category 𝒪S, Pacific J. Math. 132 (1988), 319–342.CrossRefGoogle Scholar
[23]Jantzen, J. C., Einhüllende Algebren halbeinfacher Lie-Algebren, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), vol. 3 (Springer, Berlin, 1983).CrossRefGoogle Scholar
[24]Khomenko, O. and Mazorchuk, V., On Arkhipov’s and Enright’s functors, Math. Z. 249 (2005), 357–386.CrossRefGoogle Scholar
[25]Khovanov, M., A categorification of the Jones polynomial, Duke Math. J. 101 (2000), 359–426.CrossRefGoogle Scholar
[26]Khovanov, M., A functor-valued invariant of tangles, Algebr. Geom. Topol. 2 (2002), 665–741 (electronic).CrossRefGoogle Scholar
[27]Khovanov, M., Crossingless matchings and the cohomology of (n,n) Springer varieties, Commun. Contemp. Math. 6 (2004), 561–577.CrossRefGoogle Scholar
[28]Khovanov, M., Mazorchuk, V. and Stroppel, C., A categorification of integral Specht modules, Proc. Amer. Math. Soc. 136 (2008), 1163–1169.CrossRefGoogle Scholar
[29]Mazorchuk, V., Ovsienko, S. and Stroppel, C., Quadratic duals, Koszul dual functors, and applications, Trans. Amer. Math. Soc. 361 (2009), 1129–1172, math.RT/0603475.CrossRefGoogle Scholar
[30]Mazorchuk, V. and Stroppel, C., Translation and shuffling of projectively presentable modules and a categorification of a parabolic Hecke module, Trans. Amer. Math. Soc. 357 (2005), 2939–2973.CrossRefGoogle Scholar
[31]Mazorchuk, V. and Stroppel, C., Projective–injective modules, Serre functors and symmetric algebras, J. Reine Angew. Math. 616 (2008), 131–165, math.RT0508119.Google Scholar
[32]Murphy, G. E., The representations of Hecke algebras of type A n, J. Algebra 173 (1995), 97–121.CrossRefGoogle Scholar
[33]Naruse, H., On an isomorphism between Specht module and left cell of S n, Tokyo J. Math. 12 (1989), 247–267.CrossRefGoogle Scholar
[34]Rickard, J., Morita theory for derived categories, J. London Math. Soc. (2) 39 (1989), 436–456.CrossRefGoogle Scholar
[35]Rickard, J., Translation functors and equivalences of derived categories for blocks of algebraic groups, in Finite-dimensional algebras and related topics (Ottawa, 1992), NATO Advanced Science Institute Series C: Mathematical and Physical Sciences, vol. 424 (Kluwer, Dordrecht, 1994), 255–264.CrossRefGoogle Scholar
[36]Rocha-Caridi, A., Splitting criteria for 𝔤-modules induced from a parabolic and the Bernstein–Gel’fand–Gel’fand resolution of a finite-dimensional, irreducible 𝔤-module, Trans. Amer. Math. Soc. 262 (1980), 335–366.Google Scholar
[37]Rouquier, R., Categorification of the braid groups, in Trends in Representation Theory of Algebras and Related Topics, Contemporary Mathematics, vol. 406 (American Mathematical Society, Providence, RI, 2006), 137–167.CrossRefGoogle Scholar
[38]Soergel, W., Kategorie 𝒪, perverse Garben und Moduln über den Koinvarianten zur Weylgruppe, J. Amer. Math. Soc. 3 (1990), 421–445.Google Scholar
[39]Soergel, W., The combinatorics of Harish-Chandra bimodules, J. Reine Angew. Math. 429 (1992), 49–74.Google Scholar
[40]Soergel, W., Kazhdan–Lusztig polynomials and a combinatorics for tilting modules, Represent. Theory 1 (1997), 83–114 (electronic).CrossRefGoogle Scholar
[41]Springer, T. A., Trigonometric sums, Green functions of finite groups and representations of Weyl groups, Invent. Math. 36 (1976), 173–207.CrossRefGoogle Scholar
[42]Springer, T. A., A construction of representations of Weyl groups, Invent. Math. 44 (1978), 279–293.CrossRefGoogle Scholar
[43]Stroppel, C., Category 𝒪: gradings and translation functors, J. Algebra 268 (2003), 301–326.CrossRefGoogle Scholar
[44]Stroppel, C., Category 𝒪: quivers and endomorphism rings of projectives, Represent. Theory 7 (2003), 322–345 (electronic).CrossRefGoogle Scholar
[45]Stroppel, C., Categorification of the Temperley–Lieb category, tangles, and cobordisms via projective functors, Duke Math. J. 126 (2005), 547–596.CrossRefGoogle Scholar
[46]Stroppel, C., TQFT with corners and tilting functors in the Kac–Moody case, Preprint (2006), math.RT/0605103.Google Scholar
[47]Tanisaki, T., Defining ideals of the closures of the conjugacy classes and representations of the Weyl groups, Tôhoku Math. J. (2) 34 (1982), 575–585.CrossRefGoogle Scholar