We give a new q-analogue of the (A.2) supercongruence of Van Hamme. Our proof employs Andrews’ multiseries generalisation of Watson’s
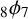 $_{8}\phi _{7}$
transformation, Andrews’ terminating q-analogue of Watson’s
$_{8}\phi _{7}$
transformation, Andrews’ terminating q-analogue of Watson’s
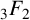 $_{3}F_{2}$
summation, a q-Watson-type summation due to Wei–Gong–Li and the creative microscoping method, developed by the author and Zudilin [‘A q-microscope for supercongruences’, Adv. Math. 346 (2019), 329–358]. As a conclusion, we confirm a weaker form of Conjecture 4.5 by the author [‘Some generalizations of a supercongruence of van Hamme’, Integral Transforms Spec. Funct. 28 (2017), 888–899].
$_{3}F_{2}$
summation, a q-Watson-type summation due to Wei–Gong–Li and the creative microscoping method, developed by the author and Zudilin [‘A q-microscope for supercongruences’, Adv. Math. 346 (2019), 329–358]. As a conclusion, we confirm a weaker form of Conjecture 4.5 by the author [‘Some generalizations of a supercongruence of van Hamme’, Integral Transforms Spec. Funct. 28 (2017), 888–899].
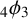 $_4\phi _3$ IDENTITY
$_4\phi _3$ IDENTITY
 $\boldsymbol F_3$
$\boldsymbol F_3$
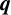 $\boldsymbol {q}$
-ANALOGUE OF VAN HAMME’S (A.2) SUPERCONGRUENCE
$\boldsymbol {q}$
-ANALOGUE OF VAN HAMME’S (A.2) SUPERCONGRUENCE
 $q$-ANALOGUE OF A DWORK-TYPE SUPERCONGRUENCE
$q$-ANALOGUE OF A DWORK-TYPE SUPERCONGRUENCE
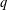 $q$-ANALOGUE OF A HYPERGEOMETRIC CONGRUENCE
$q$-ANALOGUE OF A HYPERGEOMETRIC CONGRUENCE