The goal of this paper is to go further in the analysis of the behavior of the number of descents in a random permutation. Via two different approaches relying on a suitable martingale decomposition or on the Irwin–Hall distribution, we prove that the number of descents satisfies a sharp large-deviation principle. A very precise concentration inequality involving the rate function in the large-deviation principle is also provided.

The factorially normalized Bernoulli polynomials 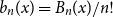$b_n(x) = B_n(x)/n!$ are known to be characterized by 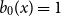$b_0(x) = 1$ and 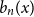$b_n(x)$ for 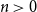$n \gt 0$ is the anti-derivative of 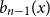$b_{n-1}(x)$ subject to 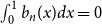$\int _0^1 b_n(x) dx = 0$. We offer a related characterization: 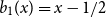$b_1(x) = x - 1/2$ and 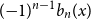$({-}1)^{n-1} b_n(x)$ for 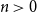$n \gt 0$ is the $n$-fold circular convolution of 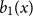$b_1(x)$ with itself. Equivalently, 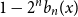$1 - 2^n b_n(x)$ is the probability density at 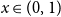$x \in (0,1)$ of the fractional part of a sum of $n$ independent random variables, each with the beta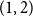$(1,2)$ probability density 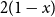$2(1-x)$ at 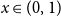$x \in (0,1)$. This result has a novel combinatorial analog, the Bernoulli clock: mark the hours of a 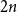$2 n$ hour clock by a uniformly random permutation of the multiset 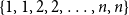$\{1,1, 2,2, \ldots, n,n\}$, meaning pick two different hours uniformly at random from the 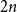$2 n$ hours and mark them 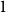$1$, then pick two different hours uniformly at random from the remaining 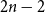$2 n - 2$ hours and mark them 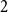$2$, and so on. Starting from hour 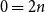$0 = 2n$, move clockwise to the first hour marked 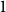$1$, continue clockwise to the first hour marked 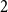$2$, and so on, continuing clockwise around the Bernoulli clock until the first of the two hours marked $n$ is encountered, at a random hour 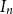$I_n$ between 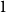$1$ and 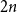$2n$. We show that for each positive integer $n$, the event 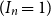$( I_n = 1)$ has probability 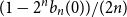$(1 - 2^n b_n(0))/(2n)$, where 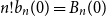$n! b_n(0) = B_n(0)$ is the $n$th Bernoulli number. For 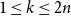$ 1 \le k \le 2 n$, the difference 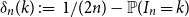$\delta _n(k)\,:\!=\, 1/(2n) -{\mathbb{P}}( I_n = k)$ is a polynomial function of 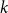$k$ with the surprising symmetry 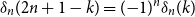$\delta _n( 2 n + 1 - k) = ({-}1)^n \delta _n(k)$, which is a combinatorial analog of the well-known symmetry of Bernoulli polynomials 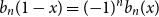$b_n(1-x) = ({-}1)^n b_n(x)$.

For a random binary noncoalescing feedback shift register of width $n$ , with all $2^{2^{n-1}}$ possible feedback functions $f$ equally likely, the process of long cycle lengths, scaled by dividing by $N=2^n$ , converges in distribution to the same Poisson–Dirichlet limit as holds for random permutations in $\mathcal{S}_N$ , with all $N!$ possible permutations equally likely. Such behaviour was conjectured by Golomb, Welch and Goldstein in 1959.

A uniform recursive tree on n vertices is a random tree where each possible $(n-1)!$ labelled recursive rooted tree is selected with equal probability. We introduce and study weighted trees, a non-uniform recursive tree model departing from the recently introduced Hoppe trees. This class generalizes both uniform recursive trees and Hoppe trees, providing diversity among the nodes and making the model more flexible for applications. We analyse the number of leaves, the height, the depth, the number of branches, and the size of the largest branch in these weighted trees.

We investigate the limit distributions associated with cost measures in Sattolo's algorithm for generating random cyclic permutations. The number of moves made by an element turns out to be a mixture of 1 and 1 plus a geometric distribution with parameter ½, where the mixing probability is the limiting ratio of the rank of the element being moved to the size of the permutation. On the other hand, the raw distance traveled by an element to its final destination does not converge in distribution without norming. Linearly scaled, the distance converges to a mixture of a uniform and a shifted product of a pair of independent uniforms. The results are obtained via randomization as a transform, followed by derandomization as an inverse transform. The work extends analysis by Prodinger.

This paper gives general conditions under which symmetric functionals of random partitions of the integer m converge in distribution as m → ∞. The main result is used to settle a conjecture of Donnelly et al. (1991) to the effect that the mean of the sum of the square roots of the relative sizes of the components of a random mapping of m integers converges to π/2 as m → ∞.

We consider s ≦ n randomly chosen permutations of the numbers 1, 2, …, n, and write them under each other, thus forming an s × n matrix, called “random-batch”. A rule, prescribing how many elements of a column may occur exactly one time, how many may occur exactly two times, etc., is called a fixpoint-structure. Assuming each possible permutation to be chosen with equal probability, the number of columns having a certain fixpoint-structure F is a random variable X(F). The limiting distribution of X(F) for n→ ∞ is considered for different cases of s = s(n). The main result (Theorem 4) says, that the common distribution of a finite number t of given fixpoint-structures tends to the product of t Poisson-laws, n→ ∞.