The Bernoulli clock: probabilistic and combinatorial interpretations of the Bernoulli polynomials by circular convolution

Abstract

The factorially normalized Bernoulli polynomials 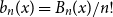$b_n(x) = B_n(x)/n!$ are known to be characterized by 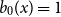$b_0(x) = 1$ and 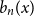$b_n(x)$ for 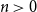$n \gt 0$ is the anti-derivative of 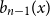$b_{n-1}(x)$ subject to 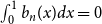$\int _0^1 b_n(x) dx = 0$. We offer a related characterization: 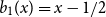$b_1(x) = x - 1/2$ and 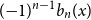$({-}1)^{n-1} b_n(x)$ for 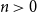$n \gt 0$ is the $n$-fold circular convolution of 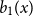$b_1(x)$ with itself. Equivalently, 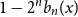$1 - 2^n b_n(x)$ is the probability density at 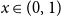$x \in (0,1)$ of the fractional part of a sum of $n$ independent random variables, each with the beta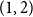$(1,2)$ probability density 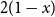$2(1-x)$ at 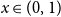$x \in (0,1)$. This result has a novel combinatorial analog, the Bernoulli clock: mark the hours of a 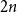$2 n$ hour clock by a uniformly random permutation of the multiset 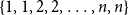$\{1,1, 2,2, \ldots, n,n\}$, meaning pick two different hours uniformly at random from the 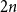$2 n$ hours and mark them 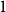$1$, then pick two different hours uniformly at random from the remaining 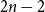$2 n - 2$ hours and mark them 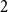$2$, and so on. Starting from hour 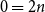$0 = 2n$, move clockwise to the first hour marked 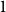$1$, continue clockwise to the first hour marked 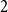$2$, and so on, continuing clockwise around the Bernoulli clock until the first of the two hours marked $n$ is encountered, at a random hour 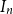$I_n$ between 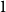$1$ and 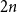$2n$. We show that for each positive integer $n$, the event 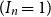$( I_n = 1)$ has probability 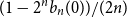$(1 - 2^n b_n(0))/(2n)$, where 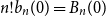$n! b_n(0) = B_n(0)$ is the $n$th Bernoulli number. For 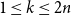$ 1 \le k \le 2 n$, the difference 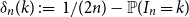$\delta _n(k)\,:\!=\, 1/(2n) -{\mathbb{P}}( I_n = k)$ is a polynomial function of 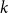$k$ with the surprising symmetry 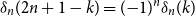$\delta _n( 2 n + 1 - k) = ({-}1)^n \delta _n(k)$, which is a combinatorial analog of the well-known symmetry of Bernoulli polynomials 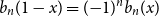$b_n(1-x) = ({-}1)^n b_n(x)$.

1. Introduction

The Bernoulli polynomials $(B_n(x))_{n \geq 0}$ are a special sequence of univariate polynomials with rational coefficients. They are named after the Swiss mathematician Jakob Bernoulli (1654–1705), who (in his Ars Conjectandi published posthumously in Basel 1713) found the sum of $m$ th powers of the first $n$ positive integers using the instance $x = 1$ of the power sum formula

(1.1) \begin{equation} \sum _{k=0}^{n-1} (x+k)^{m} = \frac{ B_{m+1} (x+n) - B_{m+1}(x) }{ m + 1}, \qquad (n = 1,2, \ldots, m = 0,1,2, \ldots ) . \end{equation}

The evaluations $B_m\,:\!=\, B_m(0)$ and $B_m(1) = ({-}1)^{m} B_m$ are known as the Bernoulli numbers, from which the polynomials are recovered as

(1.2) \begin{equation} B_n(x) = \sum _{k=0}^{n} \binom{n}{k} B_{n-k} \ x^k. \end{equation}

These polynomials have been well studied, starting from the early work of Faulhaber, Bernoulli, Seki and Euler in the $17$ th and early $18$ th centuries. They can be defined in multiple ways. For example, Euler defined the Bernoulli polynomials by their exponential generating function

(1.3) \begin{equation} B(x,\lambda ) \,:\!=\, \frac{\lambda e^{\lambda x } }{e^{\lambda } - 1} = \sum _{n = 0}^{\infty } \frac{ B_n(x) }{n!} \lambda ^n \qquad \qquad (|\lambda | \lt 2 \pi ). \end{equation}

Beyond evaluating power sums, the Bernoulli numbers and polynomials are useful in other contexts and appear in many areas in mathematics, among which we mention number theory [1, 2, 4, 28], Lie theory [6, 7, 27, 36], algebraic geometry and topology [17, 29], probability [5, 19, 20, 25, 26, 34, 39] and numerical approximation [33, 38].

The factorially normalised Bernoulli polynomials $b_n(x)\,:\!=\, B_n(x)/n!$ can also be defined inductively as follows (see [30, §9.5]). Beginning with $b_0(x) = B_0(x) = 1$ , for each positive integer $n$ , the function $x \mapsto b_n(x)$ is the unique anti-derivative of $x \mapsto b_{n-1}(x)$ that integrates to $0$ over $[0,1]$ :

(1.4) \begin{equation} b_0(x) = 1, \quad \frac{ d }{ d x } b_n(x) = b_{n-1} (x) \quad \mbox{and} \quad \int _0^1 b_n(x) = 0 \qquad (n \gt 0) . \end{equation}

So the first few polynomials $b_n(x)$ are

\begin{align*} b_0(x) &= 1, &b_1(x) &= x - 1/2,\\[3pt] b_2(x) &= \frac{1}{2!}(x^2 - x - 1/6), &b_3(x) &= \frac{1}{3!}(x^3 - 3 x^2/2 + x/2). \end{align*}

As shown in [30, Theorem 9.7] starting from (1.4), the functions $f(x) = b_n(x)$ with argument $x \in [0,1)$ are also characterised by the simple form of their Fourier transform

(1.5) \begin{equation} \widehat{f}(k) \,:\!=\, \int _{0}^{1} f(x) e^{- 2 \pi i k x} dx \qquad (k \in \mathbb{Z}) \end{equation}

which is given by

(1.6) \begin{equation} \begin{alignedat}{2} \widehat{b}_0(k) &= 1[ k = 0], \qquad &\mbox{for } k \in \mathbb{Z} ; \\[3pt] \widehat{b}_n(0) &= 0 \quad \text{and} \quad \widehat{b}_n(k) = - \frac{1}{(2 \pi i k)^n}, \qquad &\mbox{for } n \gt 0 \mbox{ and } k \ne 0, \end{alignedat} \end{equation}

with the notation $1[\dots ]$ equal to $1$ if $[\dots ]$ holds and $0$ otherwise. It follows from the Fourier expansion of $b_{n}(x)$ :

\begin{equation*} b_n(x) = - \frac {2}{(2\pi )^n} \sum _{k = 1}^{\infty } \frac {1}{k^n} \cos \left (2k\pi x - \frac {n\pi }{2}\right ) \end{equation*}

that there exists a constant $C \gt 0$ such that

(1.7) \begin{equation} \sup \limits _{0 \leq x \leq 1} \left | (2\pi )^n b_n(x) + 2\cos \left (2 \pi x - \frac{n\pi }{2}\right ) \right | \leq C 2^{-n} \quad \text{for } n \geq 2, \end{equation}

see [22]. So as $n \uparrow \infty$ the polynomials $b_n(x)$ looks like shifted cosine functions. Besides (1.3) and (1.4), several other characterisations of the Bernoulli polynomials are described in [10, 23].

This article first draws attention to a simple characterisation of the Bernoulli polynomials by circular convolution and, more importantly, provides an interesting probabilistic and combinatorial interpretation in terms of statistics of random permutations of a multiset.

For a pair of functions $f = f(u)$ and $g = g(u)$ , defined for $u$ in $[0,1)$ identified with the circle group ${\mathbb{T}}\,:\!=\,{\mathbb{R}}/\mathbb{Z} = [0,1)$ , with $f$ and $g$ integrable with respect to Lebesgue measure on $\mathbb{T}$ , their circular convolution $f\circledast g$ is the function

(1.8) \begin{equation} (f \circledast g )(u) = \int _{{\mathbb{T}}} f(v) g (u-v) dv \qquad \text{for } u \in{\mathbb{T}}. \end{equation}

Here $u-v$ is evaluated in the circle group $\mathbb{T}$ , that is modulo $1$ , and $dv$ is the shift-invariant Lebesgue measure on $\mathbb{T}$ with total measure $1$ . Iteration of this operation defines the $n$ th convolution power $u \mapsto f^{\circledast n}(u)$ for each positive integer $n$ , each integrable $f$ , and $u \in{\mathbb{T}}$ .

Theorem 1.1. The factorially normalised Bernoulli polynomials $b_n(x) = \frac{B_n(x)}{n!}$ are characterised by:

1. 1. $b_0(x) = 1$ and $b_1(x) = x - 1/2$ ,

2. 2. for $n \gt 0$ the $n$ -fold circular convolution of $b_1(x)$ with itself is $({-}1)^{n-1} b_n(x)$ ; that is

   (1.9) \begin{equation} b_n(x) = ({-}1)^{n-1} b_1^{\circledast n}(x). \end{equation}

In view of the identity $\widehat{f \circledast g} = \widehat{f} \ \widehat{g}$ , Theorem 1.1 follows from the classical Fourier evaluation (1.6) and uniqueness of the Fourier transform. A more elementary proof of Theorem 1.1, without Fourier transforms, is provided in Section 2. So the Fourier evaluation (1.6) may be regarded as a corollary of Theorem 1.1. That theorem can also be reformulated as follows:

Corollary 1.2. The following identities hold for circular convolution of factorially normalised Bernoulli polynomials:

\begin{align*} b_0(x) \circledast b_0(x) &= b_0(x)\\[3pt] b_0(x) \circledast b_n(x) &= 0, \quad (n \geq 1),\\[3pt] b_n(x) \circledast b_m(x) &= - b_{n + m}(x), \quad (n, m \geq 1).\\[3pt] \end{align*}

In particular, for positive integers $n$ and $m$ , this evaluation of $(b_n \circledast b_m)(1)$ yields an identity which appears in [32, p. 31]:

(1.10) \begin{equation} ({-}1)^{m} \int _{0}^{1} b_n(u) b_m(u) du = \int _{0}^{1} b_n(u) b_m(1-u) du = - b_{n+m}(1) . \end{equation}

Here the first equality is due to the well-known reflection symmetry of the Bernoulli polynomials

(1.11) \begin{equation} ({-}1)^m b_m(u) = b_m(1-u) \qquad (m \ge 0 ) \end{equation}

which is the identity of coefficients of $\lambda ^m$ in the elementary identity of Eulerian generating functions

(1.12) \begin{equation} B(u, - \lambda ) = \frac{ ({-}\lambda ) e^{-\lambda u } }{ e^{- \lambda } - 1} = \frac{ \lambda e^{\lambda (1-u) } }{ e^{\lambda } - 1 } = B(1-u,\lambda ). \end{equation}

The rest of this article is organised as follows. Section 2 gives an elementary proof for Theorem 1.1, and discusses circular convolution of polynomials. In Section 3 we highlight the fact that $1 - 2^n b_n(x)$ is the probability density at $x \in (0,1)$ of the fractional part of a sum of $n$ independent random variables, each with the beta $(1,2)$ probability density $2(1-x)$ at $x \in (0,1)$ . Because the minimum of two independent uniform $[0,1]$ variables has this beta $(1,2)$ probability density the circular convolution of $n$ independent beta $(1,2)$ variables is closely related to a continuous model we call the Bernoulli clock: Spray the circle ${\mathbb{T}} = [0,1)$ of circumference $1$ with $2n$ i.i.d uniform positions $U_1, U^{\prime}_1, \dots, U_n, U^{\prime}_n$ with order statistics

\begin{equation*} U_{1:2n} \lt \cdots \lt U_{2n:2n}. \end{equation*}

Starting from the origin $0$ , move clockwise to the first of position of the pair $(U_1, U^{\prime}_1)$ , continue clockwise to the first position of the pair $(U_2, U^{\prime}_2)$ , and so on, continuing clockwise around the circle until the first of the two positions $(U_n,U^{\prime}_n)$ is encountered at a random index $1 \leq I_n \leq 2n$ (i.e. we stop at $U_{I_n:2n}$ ) after having made a random number $0 \leq D_n \leq n - 1$ turns around the circle. Then for each positive integer $n$ , the event $( I_n = 1)$ has probability

\begin{equation*}{\mathbb {P}}(I_n = 1 ) = \frac { 1 - 2^n b_n(0) }{2n}\end{equation*}

where $n! b_n(0) = B_n(0)$ is the $n$ th Bernoulli number. For $ 1 \le k \le 2 n$ , the difference

\begin{equation*}\delta _{k:2n} \,:\!=\, \frac {1}{2n} - {\mathbb {P}}(I_n = k) \end{equation*}

is a polynomial function of $k$ , which is closely related to $b_n(x)$ . In particular, this difference has the surprising symmetry

\begin{equation*}\delta _{2 n + 1 - k : 2n} = ({-}1)^n \delta _{k:2n}, \quad \mbox {for } 1 \leq k \leq 2n\end{equation*}

which is a combinatorial analogue of the reflection symmetry (1.11) for the Bernoulli polynomials.

Stripping down the clock model, the random variables $I_n$ and $D_n$ are two statistics of permutations of the multiset

(1.13) \begin{equation} 1^2 \dots n^2\,:\!=\, \{1,1, 2,2, \ldots, n,n\}. \end{equation}

Section 4 discusses the combinatorics behind the distributions of $I_n$ and $D_n$ . In Section 5 we generalise the Bernoulli clock model to offer a new perspective on the work of Horton and Kurn [18] and the more recent work of Clifton et al [8]. In particular, we provide a probabilistic interpretation for the permutation counting problem in [18] and prove Conjectures 4.1 and 4.2 of [8]. Moreover, we explicitly compute the mean function on $[0,1]$ of a renewal process with i.i.d. beta( $1,m$ )-jumps. The expression of this mean function is given in terms of the complex roots of the exponential polynomial $E_m(x) \,:\!=\, 1 + x/1! + \dots + x^m/m!$ , and its derivatives at $0$ are precisely the moments of these roots, as studied in [40].

The circular convolution identities for Bernoulli polynomials are closely related to the decomposition of a realvalued random variable - $X$ into its integer part $\lfloor X \rfloor \in \mathbb{Z}$ and its fractional part $ X^\circ \in{\mathbb{T}} \,:\!=\,{\mathbb{R}}/\mathbb{Z} = [0,1)$ :

(1.14) \begin{equation} X = \lfloor X \rfloor + X^\circ . \end{equation}

If $\gamma _{1}$ is a random variable with standard exponential distribution, then for each positive real $\lambda$ we have the expansion

(1.15) \begin{equation} \frac{d}{du}{\mathbb{P}}( (\gamma _1/\lambda )^\circ \le u ) = \frac{\lambda e^{- \lambda u } }{ 1 - e^{-\lambda } } = B(u,-\lambda ) = \sum _{n \ge 0} b_n(u) ({-}\lambda )^n . \end{equation}

Here the first two equations hold for all real $\lambda \ne 0$ and $u \in [0,1)$ , but the final equality holds with a convergent power series only for $0 \lt |\lambda | \lt 2 \pi$ . Section 6 presents a generalisation of formula (1.15) with the standard exponential variable $\gamma _1$ replaced by the gamma distributed sum $\gamma _r$ of $r$ independent copies of $\gamma _1$ , for a positive integer $r$ . This provides an elementary probabilistic interpretation and proof of a formula due to Erdélyi, Magnus, Oberhettinger, and Tricomi [15, Section 1.11, page 30] relating the Hurwitz-Lerch zeta function (first studied in [24])

(1.16) \begin{equation} \Phi (z,s,u) = \sum _{m \geq 0} \frac{z^m}{(u + m)^s} \end{equation}

to Bernoulli polynomials. Moreover, the expansion (6.4) in Proposition 6.1 quantifies how the distribution of the fractional part of a $\gamma _{r,\lambda }$ random variable approaches the uniform distribution on the circle in terms of Bernoulli polynomials, where the latter are viewed as signed measures on the circle.

2. Circular convolution of polynomials

Theorem 1.1 follows easily by induction on $n$ from the characterisation (1.4) of the Bernoulli polynomials, and the action of circular convolution by the function

(2.1) \begin{equation} -b_1(u) = 1/2 - u, \end{equation}

as described by the following lemma.

Lemma 2.1. For each Riemann integrable function $f$ with domain $[0,1)$ , the circular convolution $h = f \circledast ({-}b_1)$ is continuous on $\mathbb{T}$ , implying $h(0) = h(1{-})$ . Moreover,

(2.2) \begin{equation} \int _0^1 h(u) du = 0 \end{equation}

and at each $u \in (0,1)$ at which $f$ is continuous, $h$ is differentiable with

(2.3) \begin{equation} \frac{d}{du} h(u) = f(u) - \int _0^1 f(v) dv . \end{equation}

In particular, if $f$ is bounded and continuous on $(0,1)$ , then $h = f \circledast ({-}b_1)$ is the unique continuous function $h$ on $\mathbb{T}$ subject to ( 2.2 ) with derivative ( 2.3 ) at every $u \in (0,1)$ .

Proof. According to the definition of circular convolution (1.8),

\begin{equation*} (f \circledast g )(u) = \int _0^u f(v) g (u-v) dv + \int _u^1 f(v) g(1 + u - v ) dv . \end{equation*}

In particular, for $g(u) = - b_1(u)$ , and a generic integrable function $f$ ,

\begin{align*} ( f \circledast ({-}b_1) )(u) &= \int _0^u f(v) ( v - u + 1/2) dv + \int _u^1 f(v) ( v - u - 1/2) dv \\[3pt] &= \frac{1}{2} \left [ \int _0^u f(v) d v - \int _u ^1 f(v) dv \right ] - u \int _0^1 f(v) dv + \int _0^1 v f(v) dv. \end{align*}

Differentiate this identity with respect to $u$ , to see that $h \,:\!=\, f \circledast ({-}b_1)$ has the derivative displayed in (2.3) at every $u \in (0,1)$ at which $f$ is continuous, by the fundamental theorem of calculus. Also, this identity shows $h$ is continuous on $(0,1)$ with $h(0) = h(0{+}) = h(1{-})$ , hence $h$ is continous with respect to the topology of the circle $\mathbb{T}$ . This $h$ has integral $0$ by associativity of circular convolution: $h \circledast 1 = f \circledast ({-}b_1) \circledast 1 = f \circledast 0 = 0$ . Assuming further that $f$ is bounded and continuous on $(0,1)$ , the uniqueness of $h$ is obvious.

The reformulation of Theorem 1.1 in Corollary 1.2 displays how simple it is to convolve Bernoulli polynomials on the circle. On the other hand, convolving monomials is less pleasant, as the following calculations show.

Lemma 2.2. For real parameters $n \gt 0$ and $m \gt - 1$ ,

(2.4) \begin{equation} {x^m} \circledast{x^n} ={x^n} \circledast{x^m} = \frac{n}{m+1}{x^{n-1}} \circledast{x^{m+1}} + \frac{{x^n} -{x^{m+1}} }{m+1}. \end{equation}

Proof. Integrate by parts to obtain

\begin{align*}{x^n} \circledast{x^m} &= \int _{0}^{x} u^{n} (x - u)^m du + \int _{x}^{1} u^{n} (1 + x - u)^m du \\[3pt] &= \frac{n}{m+1}\int _{0}^{x} u^{n-1} (x - u)^{m+1} du + \frac{n}{m+1} \int _{x}^{1} u^{n-1} (1 + x - u)^m du + \frac{x^n - x^{m+1}}{m+1} \end{align*}

and hence (2.4).

Proposition 2.3 (Convolving monomials). For each positive integer $n$

(2.5) \begin{equation} {1} \circledast{x^n} ={x^n} \circledast{1} = \frac{1}{n+1}, \end{equation}

and for all positive integers $m$ and $n$

(2.6) \begin{equation} {x^m} \circledast{x^n} ={x^n} \circledast{x^m} = \frac{n! \ m!}{(n+m+1)!} + \sum _{k = 0}^{n-1} \frac{n!}{ (n-k)! (m+1)_{k+1}} ({x}^{n-k} -{x}^{m+k+1}) \end{equation}

and with the Pochhammer notation $(m+1)_{k+1} \,:\!=\, (m+1) \dots (m+k+1)$ . In particular

\begin{equation*} {x} \circledast {x^n} = \frac { {x} - {x}^{n+1} }{n+1} + \frac {1}{(n+1)(n+2)}. \end{equation*}

Proof. By induction, using Lemma 2.2.

Remark 2.4.

1. 1. By inspection of (2.6) the polynomial $\left ({x^n} \circledast{x^m} - \frac{n! \ m!}{(n+m+1)!}\right )/ x$ is an anti-reciprocal polynomial with rational coefficients.

2. 2. Theorem 1.1 can be proved by inductive application of Proposition 2.3 to the expansion of the Bernoulli polynomials $B_n(x)$ in the monomial basis. This argument is unnecessarily complicated, but boils down to two following identities for the Bernoulli numbers $B_n\,:\!=\, B_n(0)$ for $n \geq 1$ :

   (2.7) \begin{equation} B_{n} = \frac{-1}{n + 1} \sum _{k = 0}^{n-1} \binom{n+1}{k} B_{k} \end{equation}
   (2.8) \begin{equation}\frac{B_{n+1}}{(n+1)!} = - \sum _{k = 0}^{n} \frac{1}{(k+2)!} \frac{B_{n-k}}{(n-k)!}. \end{equation}
   The identity (2.7) is a commonly used recursion for the Bernoulli numbers. We do not know any reference for (2.8), but this can be checked by manipulation of Euler’s generating function (1.3). We refer the reader to Section A for more details.

3. 3. Using the hypergeometric function $F \,:\!=\,{}_{2}{F}_1$ , it follows from Equation (2.6) that:

   \begin{align*} x^{n} \circledast x^m & = \frac {n! m!}{(m+n+1)!} x^{m+n+1} + \frac {x^{n}}{m+1} F\left (1,-n;\,m+2;\, \frac {-1}{x}\right )\nonumber\\[3pt]& \quad - \frac {x^{m+1}}{m+1} F(1,-n;\,m+2;\,-x).\end{align*}

3. Probabilistic interpretation

For positive real numbers $a,b \gt 0$ , recall that the beta $(a,b)$ probability distribution, has density

\begin{equation*} \frac {\Gamma (a)\Gamma (b)}{\Gamma (a+b)} \ x^{a-1} (1-x)^{b-1}, \quad ( 0 \leq x \leq 1) \end{equation*}

with respect the the Lebesgue measure on $\mathbb{R}$ , where $\Gamma$ denotes Euler’s gamma function [3] :

\begin{equation*} \Gamma (x) = \int _{0}^{\infty } t^{x-1} e^{-t} dt, \quad \text {for } x \gt 0. \end{equation*}

The following corollary offers a probabilistic interpretations of Theorem 1.1 in terms of the fractional part of a sum of $n$ i.i.d beta $(1,2)$ -distributed random variables on the circle.

Corollary 3.1. The probability density of the sum of $n$ independent beta $(1,2)$ random variables in the circle ${\mathbb{T}} ={\mathbb{R}}/ \mathbb{Z}$ is

\begin{equation*} (1 - 2 b_1)^{\circledast n}(u) = 1 - 2^n b_n(u), \quad \text {for } u \in {\mathbb {T}} = [0,1). \end{equation*}

Proof. Note that $b_0(u) = 1$ and the density of a beta $(1,2)$ random variable is $2(1 - u) = 1 - 2b_1(u)$ for $0 \lt u \lt 1$ . So the result follows by induction from Corollary 1.2.

Recall that a beta( $1,2$ ) random variable can be constructed as the minimum of two independent uniform random variables in $[0,1]$ . Let $U_1, U^{\prime}_{1}, \dots,U_n,U^{\prime}_{n}$ be a sequence of $2n$ i.i.d random random variables with uniform distribution on ${\mathbb{T}} = [0,1)$ . We think of these variables as random positions around a circle of circumference $1$ . On the event of probability one that the $U_i$ and $U^{\prime}_i$ are all distinct, we define the following variables:

1. 1. $U_{1:2n} \lt U_{2:2n} \lt \cdots \lt U_{2n:2n}$ the order statistics of the variables $U_1, U^{\prime}_1, \dots, U_n, U^{\prime}_n$ ,

2. 2. $X_1 \,:\!=\, \min (U_1, U^{\prime}_1)$

3. 3. for $2 \le k \le n$ , the variable $X_{k}$ is the spacing around the circle from $X_{k-1}$ to whichever of $U_{k}, U^{\prime}_{k}$ is encountered first moving clockwise around $\mathbb{T}$ from $X_{k-1}$ ,

4. 4. $I_k$ is the random index in $\{1, \dots, 2n\}$ such that $X_k = U_{I_k:2n}$ .

5. 5. $D_n \in \{0, \dots, n-1 \}$ is the random number of full rotations around $\mathbb{T}$ to find $X_n$ . This is also the number of descents in the sequence $(I_1,I_2, \dots, I_n)$ ; that is

   (3.1) \begin{equation} D_n = \sum _{i = 1}^{n-1} 1[I_{i} \gt I_{i+1}]. \end{equation}

We refer to this construction as the Bernoulli clock. Figure 1 depicts an instance of the Bernoulli clock for $n=4$ .

Figure 1. The clock is a circle of circumference $1$ . Inside the circle the numbers $1,2, \ldots, 8$ index the order statistics of $8$ uniformly distributed random points on the circle. The corresponding numbers outside the circle are a random assignment of labels from the multiset of four pairs $1^2 2^2 3^2 4^2$ . The four successive arrows delimit segments of ${\mathbb{T}} \equiv [0,1)$ whose lengths $X_1,X_2,X_3,X_4$ are independent beta $(1,2)$ random variables, while $(I_1,I_2,I_3,I_4)$ is the sequence of indices inside circle, at the end points of these four arrows. In this example, $(I_1,I_2,I_3,I_4) = (1,4,6,3)$ , and the number of turns around the circle is $D_4 = 1$ .

Proposition 3.2. With the above notation, the following hold

1. 1. The random spacings $X_1, X_2, \dots, X_n$ (defined by the Bernoulli clock above) are i.i.d beta( $1,2$ ) random variables.

2. 2. The random sequence of indices $(I_1, I_2, \dots, I_n)$ is independent of the sequence of order statistics $(U_{1:2n}, \dots, U_{2n:2n})$ .

Proof. This is a corollary of Proposition 5.2. See Section 5 where the general case is discussed.

3.1. Expanding Bernoulli polynomials in the Bernstein basis

It is well known that, for $1 \leq k \leq 2n$ the distribution of $U_{k:2n}$ is beta( $k, 2n+1-k$ ), whose probability density relative to Lebesgue measure at $u \in [0,1)$ is the normalised Bernstein polynomial of degree $2 n - 1$

\begin{equation*} f_{k:2n}(u) \,:\!=\, \frac {(2n)!}{(k-1)!(2n - k)!} u^{k - 1}(1-u)^{2n - k} \end{equation*}

Proposition 3.3. For each positive integer $n$ , the sum $S_n$ of $n$ independent beta $(1,2)$ variables has fractional part $S_n^\circ$ whose probability density on $(0,1)$ is given by the formulas

(3.2) \begin{equation} f_{S_n}^\circ (u) = 1 - 2^n b_n(u) = \sum _{k = 1}^{2n} p_{k:2n} \ f_{k:2n}(u), \quad \text{for } u \in (0,1). \end{equation}

where $(p_{1:2n}, \dots, p_{2n:2n})$ is the probability distribution of the random index $I_n$ in the Bernoulli clock construction:

\begin{equation*} p_{k:2n} = {\mathbb {P}}(I_n = k), \quad \text {for } 1 \leq k \leq 2n. \end{equation*}

Proof. The first formula for the density of $S_n^\circ$ is read from Corollary 3.1. Proposition 3.2 represents $S_n^\circ = U_{I_n: 2n}$ where the index $I_n$ is independent of the sequence of order statistics $(U_{k:2n}, 1 \le k \le 2 n)$ , hence the second formula for the same probability density on $(0,1)$ .

Corollary 3.4. The factorially normalised Bernoulli polynomial of degree $n$ admits the expansion in Bernstein polynomials of degree $2 n - 1$

(3.3) \begin{equation} b_{n}(u) = \frac{1}{2^n} \sum _{k = 1}^{2n} \delta _{k: 2n } \ f_{k:2n}(u) \end{equation}

where $\delta _{k:2n}$ is the difference at $k$ between the uniform probability distribution on $\{1, \dots, 2n \}$ and the distribution of $I_n$ .

(3.4) \begin{equation} \delta _{k:2n} = \frac{1}{2n} - p_{k:2n} \quad \text{for } 1 \leq k \leq 2n. \end{equation}

Proof. Formula (3.3) is obtained from (3.2), in the first instance as an identity of continuous functions of $u \in (0,1)$ , then as an identity of polynomials in $u$ , by virtue of the binomial expansion

\begin{equation*} \sum _{k=1}^{2n} \frac {1}{2n} f_{k:2n}(u) = 1. \end{equation*}

Remark 3.5. Since $b_n(1 - u) = ({-}1)^{n} b_{n}(u)$ and $f_{k:2n}(1-u) = f_{2 n + 1 - k: 2n} (u)$ , the identity (3.3) implies that the difference between the distribution of $I_n$ and the uniform distribution on $\{1, \ldots, 2 n\}$ has the symmetry

(3.5) \begin{equation} \delta _{2n + 1 - k : 2n} = ({-}1)^n \delta _{k:2n} \quad \text{for } 1 \leq k \leq 2n. \end{equation}

Conjecture 3.6. We conjecture that the discrete sequence $(\delta _{1:2n}, \dots, \delta _{2n:2n})$ approximates the Bernoulli polynomials $b_n$ (hence also the shifted cosine functions, see ( 1.7 )) as $n$ becomes large, more precisely:

\begin{equation*} \sup \limits _{1 \leq k \leq 2n} \left | 2n \pi ^n \delta _{k:2n}- (2\pi )^n b_n\left ( \frac {k-1}{2n-1}\right ) \right | \xrightarrow []{} 0 \quad \text {as } n \to \infty .\end{equation*}

Figure 3 does suggest that the difference $2n \pi ^n \delta _n(k) - (2\pi )^n b_n\left ( \frac{k-1}{2n-1}\right )$ gets smaller uniformly in $1 \leq k \leq 2n$ as $n$ grows, geometrically but rather slowly, like $C \rho ^n$ for a constant $C \gt 0$ and $\rho \approx 2^{- 1/100}$ .

Figure 2. Plots of $2n \pi ^n \delta _n$ (dotted curve in blue), $(2\pi )^n b_n(x)$ (curve in red) and their difference (dotted curve in black) for $n = 70, 75, 80, 85$ .

Figure 3. Plots of $2n \pi ^n \delta _{k:2n}$ $- (2\pi )^n b_n$ $(\frac{k-1}{2n -1 })$ for $n = 100, 200, 300,$ $ 400, 500, 600$ .

From (3.2) we see that we can expand the polynomial density $1 -2^n b_n(u)$ in the Bernstein basis of degree $2n - 1$ with positive coefficients. A similar expansion can obviously be achieved using Bernstein polynomials of degree $n$ , with coefficients which must add to $1$ . These coefficients are easily calculated for modest values of $n$ (see (3.8)) which suggests the following

Conjecture 3.7. For each positive integer $n$ , the polynomial probability density $1 -2^n b_n(u)$ on $[0,1)$ can be expanded in the Bernstein basis of degree $n$ with positive coefficients.

Question 3.8. More generally, what can be said about the greatest multiplier $c_n$ such that the polynomial $1 - c_n b_n(x)$ is a linear combination of degree $n$ Bernstein polynomials with non-negative coefficients?

3.2. The distributions of $I_n$ and $D_n$

Proposition 3.9. The distribution of $I_n$ in the Bernoulli clock construction is given by

(3.6) \begin{equation} {\mathbb{P}}( I_n = k ) = \frac{1}{2n} - \delta _{k:2n} \quad \text{for } 1 \leq k \leq 2n \mbox{ with } \end{equation}

(3.7) \begin{equation} \delta _{k:2n} = \frac{2^{n-1}}{n \ n!}\sum _{i = 0}^{n} \frac{\binom{k-1}{i} \binom{n}{i} }{ \binom{2n - 1}{i}} B_{n-i}, \quad \text{ for } 1 \leq k \leq 2n. \end{equation}

Proof. For each positive integer $N$ , in the Bernstein basis $(f_{j:N})_{1 \leq j \leq N}$ of polynomials of degree at most $N-1$ , it is well known that the monomial $x^i$ can be expressed as

\begin{equation*} x^i = \frac {1}{N \binom {N - 1}{i}} \sum _{j = i+1}^{N} \binom {j-1}{i} f_{j:N}(x) \quad \text {for } 0 \leq i \lt N, \end{equation*}

see [35, Table 2.1] for a reference. Plugging this expansion into (1.2) yields the expansion of $b_n(x)$ in the Bernstein basis of degree $N-1$ for every $N \gt n$

(3.8) \begin{equation} b_n(x) = \sum _{j = 1}^N \left (\sum _{i = 0}^{n} \frac{\binom{j-1}{i} \binom{n}{i}}{ n! N \binom{N - 1}{i}} B_{n-i} \right ) f_{j:N}(x) \qquad ( 0 \le n \lt N). \end{equation}

In particular, for $N = 2 n$ comparison of this formula with (3.3) yields (3.7) and hence (3.6)

Remark 3.10. The error $\delta _{k:2n}$ is polynomial in $k$ and the symmetry $\delta _{2n + 1 - j : 2n} = ({-}1)^n \delta _{j : 2n}$ is not obvious from (3.7).

Let us now derive the distribution of $D_n$ explicitly. From the Bernoulli clock scheme, we can construct the random variable $D_n$ as follows. Let $X_1, \dots, X_n$ be a sequence of i.i.d random variables and $S_n \,:\!=\, X_1 + \dots + X_n$ their sum in $\mathbb{R}$ (not in the circle $\mathbb{T}$ ), then

\begin{equation*} D_n = \lfloor S_n \rfloor . \end{equation*}

Theorem 3.11. The distribution function of $S_n$ is given by

\begin{equation*} {\mathbb {P}}(S_n \leq x) = 2^n \sum _{k =0}^{n}\sum _{ j = 0}^{n-k} \binom {n}{k} \binom {n-k}{j} ({-}1)^{n-k-j} \frac {(x-k)_+^{2n - j}}{(2n-j)!}, \quad \quad \text {for } x \geq 0, \end{equation*}

where $x_{+}$ denotes $\max\! (x,0)$ for $x \in{\mathbb{R}}$ .

Proof. Let $\varphi$ be the Laplace transform of the $X_i$ ’s i.e.

\begin{equation*} \varphi _X(\theta ) \,:\!=\, \mathbb {E}[e^{- \theta X_1}] = \int _{0}^{+ \infty } \theta e^{-\theta t} {\mathbb {P}}(X_1 \leq t) dt, \quad \text {for } \theta \gt 0. \end{equation*}

We compute $\varphi _{X}$ and we obtain

\begin{equation*} \varphi _X(\theta ) = \frac {2}{\theta ^2} \left ( e^{- \theta } + (\theta - 1) \right ), \quad \text {for } \theta \gt 0. \end{equation*}

So for $n \geq 1$ , the Laplace transform of $S_n$ is then given by

(3.9) \begin{equation} \varphi _{S_n}(\theta ) = \left (\varphi _X(\theta )\right )^n = 2^n \sum _{k =0}^{n}\sum _{ j = 0}^{n-k} \binom{n}{k} \binom{n-k}{j} ({-}1)^{n-k-j} \frac{ e^{- k \theta } }{\theta ^{2n - j}}. \end{equation}

The transform $\varphi _{S_n}$ can be inverted term by term using the following identity

(3.10) \begin{equation} \int _{0}^{+\infty } \theta e^{-\theta t} \frac{(t - k)_{+}^{n}}{n!} \ dt = \frac{e^{- k\theta }}{\theta ^n}, \quad \text{for } k \geq 0, \ \theta \gt 0 \text{ and } n \geq 0. \end{equation}

We then obtain the cdf of $S_n$ as follows:

(3.11) \begin{equation} {\mathbb{P}}(S_n \leq x) = 2^n \sum _{k =0}^{n}\sum _{ j = 0}^{n-k} \binom{n}{k} \binom{n-k}{j} ({-}1)^{n-k-j} \frac{(x-k)_+^{2n - j}}{(2n-j)!}, \quad \text{for } x \geq 0. \end{equation}

Remark 3.12. (3.10) was known to Lagrange in the 1700s and it appears in [11, Lemme III and Corollaire I] where he said the final words on inverting Laplace transforms of the form (3.9):

1. “ $\ldots$ mais comme cette intégration est facile par les methodes connues, nous n’entrerons pas dans un plus grand detail là-dessus; et nous terminerons même ici nos recherches, par lesquelles on doit voir qu’il ne reste plus de difficulté dans la solution des questions qu’on peut proposer à ce sujet.”

Since $S_n$ has a density, we can deduce that

\begin{equation*} {\mathbb {P}}(D_n = k) = {\mathbb {P}}(S_n \leq k + 1) - {\mathbb {P}}(S_n \leq k), \quad \text {for } 0 \leq k \leq n - 1. \end{equation*}

Combined with (3.11) this gives the distribution of $D_n$ explicitly. The following table gives the values of the number of permutations of the multiset $1^2 \dots n^2$ for which $D_n = d$ , which we denote by $\#(n;\, +, d)$ , for small values of $n$ .

Table 1 The table of $\#(n;\, +, d)$

Remark 3.13. The sequence $a(n) = \#(n;\, +, 0) = 2^{-n} (2n)! \ {\mathbb{P}}(D_n = 0)$ , which counts the number of permutations of $1^2 \dots n^2$ for which $D_n = 0$ (the first column in Table 1), can be explicitly written using (3.11) as follows

(3.12) \begin{equation} a(n) ={\mathbb{P}}(S_n \leq 1) = \sum _{j = 0}^{n} ({-}1)^{n-j} \binom{n}{j}\frac{ (2n)!}{(2n-j)!}. \end{equation}

This integer sequence appears in many other contexts (see OEIS entry A006902), among which we mention a few:

1. 1. $a(n)$ is the number of words on $1^2 \dots n^2$ with longest complete increasing subsequence of length $n$ . We shall detail this in Section 5.

2. 2. $a(n) = n! \ Z(\mathfrak{S}_n;\, n, n-1, \dots, 1)$ where $Z(\mathfrak{S}_n)$ is the cycle index of the symmetric group of order $n$ (see [37, Section 1.3]).

3. 3. $a(n) = \textrm{B}_n \left (n \cdot 0!, \ (n-1) \cdot 1!, \ (n-2)! \cdot 2!, \ \dots, \ 1 \cdot (n-1)! \right )$ , where $\textrm{B}_n(x_1, \dots,x_n)$ is the $n$ th complete Bell polynomial.

4. Combinatorics of the Bernoulli clock

There are a number of known constructions of the Bernoulli numbers $B_n$ by permutation enumerations. Entringer [14] showed that Euler’s presentations of the Bernoulli numbers, as coefficients in the expansions of hyperbolic and trigonometric functions, lead to explicit formulas for $B_n$ by enumeration of alternating permutations. More recently, Graham and Zang [16] gave a formula for $B_{2n}$ by enumerating a particular subset of the set of $2^{-n}(2n)!$ permutations of the multiset $1^2 \dots n^2$ of $n$ pairs.

The number of permutations of this multiset, such that for every $i \lt n$ between each pair of occurrences of $i$ there is exactly one $i+1$ , is $({-}2)^n ( 1 - 2^{2 n} )B_{2n}$ . Here we offer a novel combinatorial expression of the Bernoulli numbers based on a different attribute of permutations of same multiset (1.13), which arises from the the probabilistic interpretation in Section 3. We call the combinatorial construction involved the the Bernoulli clock. Fix a positive integer $n \geq 1$ and for a permutation $\tau$ of the multiset (1.13),

• • Let $1 \leq I_1 \leq 2n-1$ be the position of the first $1$ ; that is $I_1 = \min \{1 \leq k \leq 2n \colon \tau (k) = 1 \}$ .

• • For $1 \leq k \leq n-1$ , denote by $1 \leq I_{k+1} \leq 2n$ the index of the first value $k+1$ following $I_k$ in the cyclic order (circling back to the beginning of necessary).

• • Let $0 \leq D_n \leq n-1$ be the number of times we circled back to the beginning of the multiset before obtaining the last index $I_n$ .

Example 4.1. The permutation $\tau$ corresponding to Figure 1 is the permutation $\tau = (1,1,4,2,4,3,3,2)$ . For this permutation

\begin{equation*} (I_1,I_2,I_3,I_4) = (1,4,6,3) \quad \text {and} \quad D_4 = 1 . \end{equation*}

Notice that random index $I_n$ and the number of descents $D_n$ depend only on the relative positions of $U_1, U^{\prime}_1, \dots, U_{n},U^{\prime}_{n}$ i.e. the permutation of the multiset $1^2 \dots n^2$ . So the distribution of $I_n$ and $D_n$ can be obtained by enumerating permutations. For $n \geq, 1 \leq i \leq 2n$ and $0 \leq d \leq n-1$ , let us denote by

1. 1. $\#(n;\,i,d)$ the number of permutations among the $(2n)!/ 2^n$ permutations of the multiset $\{1,1, \dots, n,n\}$ that yield $I_n = i$ and $D_n = d$ ,

2. 2. $\#(n;\, i, {+})$ the number of permutations that yield $I_n = i$ ,

3. 3. $\#(n;\, +, d)$ the number of permutations that yield $D_n = d$ .

For $n = 2$ there are $6$ permutations of $\{1,1,2,2\}$ summarised in the following table

Table 2 Permutations of $\{1,1,2,2\}$ and corresponding values of $(I_2, D_2)$

The joint distribution of $I_2, D_2$ is then given by

Table 3 The table of $\#(2;\, \bullet, \bullet )$

Similarly for $n=3$ we get

Table 4 The table of $\#(3;\, \bullet, \bullet )$

The distribution of $(I_n, D_n)$ can be obtained recursively as follows. The key observation is that every permutation of the multiset $1^2 2^2 \dots n^2$ is obtained by first choosing a permutation of $1^2 2^2 \dots (n-1)^2$ , then choosing $2$ places to insert the two values $n,n$ . There are $\binom{2(n-1)}{2}$ options for where to insert the two last values. This corresponds to the factorisation

\begin{equation*} (2n)! \ 2^{-n} = (2(n-1))! \ 2^{-n+1} \ \binom {2n}{2}. \end{equation*}

Moreover, for $x \in \{1, \dots, 2(n-1)\}$ the identity of quadratic polynomials

\begin{equation*} \binom {x+1}{2} + \binom {2n - x}{2} + x(2n-1 - x) = \binom {2n}{2}, \end{equation*}

translates, for each integer $x \in \{1, \dots, 2(n-1)\}$ and each permutation $\sigma$ of $1^2,\dots (n-1)^2$ , the decomposition of the total number of ways to insert the next two values $n, n$ according to whether:

1. 1. both places are to the left of $x$ ,

2. 2. both places are to the right of $x$ ,

3. 3. one of those places is to the left of $x$ and the other to the right of $x$ .

Suppose we ran the Bernoulli clock scheme on $2(n-1)$ hours and obtained $(I_{n-1}, D_{n-1})$ . Inserting two new values $n, n$ , the index $I_{n}$ then depends only on $I_{n-1}$ and the places where the two new values $n$ are inserted relatively to $I_{n-1}$ . So, the sequence $(I_1, I_2, \dots )$ is a time-inhomogeneous Markov chain starting from $I_1 = 1$ and a $2(n-1) \times 2n$ transition matrix from $I_{n-1}$ to $I_n$ given by

\begin{equation*} P_{n}(x \to y) = {\mathbb {P}}(I_n = y | I_{n-1} = x) = \frac {Q_n(x,y)}{\binom {2n}{2}}, \qquad (1 \leq x \leq (2n-1), \ 1 \leq y \leq 2n) \end{equation*}

where $Q_n(x,y)$ is the number of ways to insert the two new values $n$ in the Bernoulli clock in such a way that the first one of them to the right of $x$ is at place $y$ . More explicitly, by elementary counting, we have

\begin{equation*} Q_n(x,y) = \begin {cases} x - y + 1, \quad \quad \quad \ \ \text {if } 1 \leq y \leq x \\[3pt] 2n - 1 - x, \quad \quad \quad \text {if } y = x+1 \\[3pt] 2n - y + x, \quad \quad \quad \text {if } x+2 \leq y \leq 2n \end {cases} \end{equation*}

So the first few transition matrices are

\begin{equation*} P_2 = \frac {Q_2}{\binom {4}{2}} =\frac {1}{6} \left ( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 1 & 2 & 2 & 1 \\[3pt] 2 & 1 & 1 & 2 \end {array} \right ), \quad \quad P_3 = \frac {Q_3}{\binom {6}{2}} = \frac {1}{15} \left ( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 1 & 4 & 4 & 3 & 2 & 1 \\[3pt] 2 & 1 & 3 & 4 & 3 & 2 \\[3pt] 3 & 2 & 1 & 2 & 4 & 3 \\[3pt] 4 & 3 & 2 & 1 & 1 & 4 \end {array} \right ), \end{equation*}

\begin{equation*} \text {and} \quad P_4 = \frac {Q_4}{\binom {8}{2}} = \frac {1}{28} \left ( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 1 & 6 & 6 & 5 & 4 & 3 & 2 & 1 \\[3pt] 2 & 1 & 5 & 6 & 5 & 4 & 3 & 2 \\[3pt] 3 & 2 & 1 & 4 & 6 & 5 & 4 & 3 \\[3pt] 4 & 3 & 2 & 1 & 3 & 6 & 5 & 4 \\[3pt] 5 & 4 & 3 & 2 & 1 & 2 & 6 & 5 \\[3pt] 6 & 5 & 4 & 3 & 2 & 1 & 1 & 6 \end {array} \right ), \end{equation*}

see Table 5 for a detailed combinatorial construction of $Q_3$ . This discussion is summarised by the following proposition.

Table 5 Combinatorial construction of $Q_3$ : The top $1\times 6$ row displays the column index of places in rows of the main $15 \times 6$ table below it. The $15$ rows of the main table list all $\binom{6}{2} = 15$ pairs of places, represented as two dots $\bullet$ , in which two new values $3,3$ can be inserted relative to $4$ possible places of $I_2 \in \{1, 2, 3, 4\}$ . The exponents of each dot $\bullet$ are the values of $I_2$ leading to $I_3$ being the column index of that dot in $\{1,2, 3,4,5, 6 \}$ . For example in the second row, representing insertions of the new value $3$ in places $1$ and $3$ of $6$ places, the dot $\bullet ^{2,3,4}$ in place $1$ is the place $I_3$ found by the Bernoulli clock algorithm if $I_2 \in \{2,3,4\}$ . The matrix $Q_3$ is the $4 \times 6$ matrix below the main table. The entry $Q_3(i,j)$ in row $i$ and column $j$ of $Q_3$ is the number of times $i$ appears in the exponent of a dot $\bullet$ in the $j$ th column of the main table

Proposition 4.2. For a uniform random permutation of $1^2 \dots n^2$ the probability distribution of $I_n$ , treated as a $1\times 2n$ row vector $p_n = (p_{1:2n}, \dots, p_{2n:2n})$ , is determined recursively by the matrix forward equations

(4.1) \begin{equation} p_{n+1} = p_{n} \ P_{n+1} \qquad \mbox{ for } n = 1,2, \ldots \mbox{ starting from } p_1 = (1,0). \end{equation}

So the first few of these distributions of $I_n$ are as follows:

\begin{align*} p_1 &= (1,0), & p_2 &= \frac{1}{6} (1,2,2,1), \\[3pt] p_3 &= \frac{1}{90} (15,13,14,16,17,15), & p_4 &= \frac{1}{2520} (322,322,312,304,304,312,322,322). \end{align*}

As $n$ become bigger, the distribution $p_{n}$ gets closer to the uniform on $\{1, \dots, 2n\}$ . The error $\delta _n(k) = 1/(2n) - p_{k:2n}$ is polynomial in $k$ and satisfies the same forward equation as $p_n$ i.e.

(4.2) \begin{equation} \delta _{n+1} = \delta _{n} \ P_{n+1} \qquad \mbox{ for } n = 1,2, \ldots \mbox{ starting from } \delta _0 = (1/2,-1/2). \end{equation}

The sequence $\delta _n$ is also closely tied to the polynomial $b_n(x)$ as (3.3) shows.

Example 4.3. Let us detail the combinatorics of permutations that yields the matrix $P_3$ .

Notice that the matrices $Q_n$ have the remarkable symmetry

(4.3) \begin{equation} 2n - 1 - Q_{n}(i,j) = \widetilde{Q}_{n}(i, j), \quad (1 \leq i \leq 2n, \ 1 \leq j \leq 2n+2), \end{equation}

with $\widetilde{Q}_{n}(i, j) \,:\!=\, Q_{n}(2n - 1 - i, 2n + 1 -j)$ i.e. the matrix $\widetilde{Q}_n$ is the matrix $Q_n$ with entries in reverse order in both axis.

Remark 4.4.

1. 1. It is interesting to note that, from (4.1), it is not clear what the Bernoulli polynomials have in relation with the distribution $p_{n}$ or the error $\delta _n$ . It is not also clear from this recursion, even with (4.3), that $\delta _n$ has the symmetry described in (3.5).

2. 2. Considering $\delta _n$ as a discrete analogue of $b_n$ , one can think of the equation $\delta _{n+1} = \delta _{n} \ P_{n+1}$ as a discrete analogue of the integral formula (1.4).

3. 3. In addition to the dynamics of the Markov chain $I = (I_1, I_2, \dots )$ , we can get obtain the joint distribution of $(I_n, D_n)$ recursively in the same way. The key observation is that at step $n$ , having obtained $I_n$ from the Bernoulli clock scheme and inserting the two new values $n+1$ in the clock, we either increment $D_n$ by $1$ to get $D_{n+1}$ if both values are inserted prior to $I_n$ or the number of laps is not incremented i.e. $D_{n+1} = D_n$ if one of the two values is inserted after $I_n$ . We then obtain the following recursion for $\#(n;\, i, d)$ :

   1. 1) $\#(1 ;\, 1, 0) = 1$

   2. 2) $\#(n+1;\, i, d) = \sum \limits _{1 \leq x \lt h} \#(n;\, i, x) \ \#_{n+1}(x,d) + \sum \limits _{h \leq x \leq 2n} \#(n;\, i-1, x) \ \#_{n+1}(x,d)$ .

   So one can get the joint distribution of $(I_n,D_n)$ recursively with

   \begin{equation*} {\mathbb {P}}(I_{n} = i, \ D_n = d) = \frac {\#(n;\, i, d )}{2^{-n}(2n)!}. \end{equation*}

5. Generalised Bernoulli clock

Let $n \geq 1$ , $m_1, \dots, m_n \geq 1$ be positive integers and $M = m_1 + \dots + m_n$ . Let $\tau _n = \tau (m_1, \dots, m_n)$ be a random permutation uniformly distributed among the $M!/(m_1 ! \dots m_n !)$ permutations of the multiset $1^{m_1}2^{m_2} \dots n^{m_n}$ . Let us denote by $1 \leq I_1 \leq M$ the index of the first $1$ in the sequence $\tau _n$ . Continuing from this index $I_1$ , let $I_2$ be the index of the first $2$ we encounter (circling back if necessary) and continuing in this manner we get random indices $(I_1, I_2, \dots, I_n)$ . Let us denote by $D_n = D(m_1, \dots, m_n)$ the number of times we circled around the sequence $\tau _n$ in this process, that is the number of descents in the random sequence $(I_1, I_2, \dots, I_n)$ , as in (3.1).

For the continuous model, mark the circle ${\mathbb{T}} ={\mathbb{R}}/\mathbb{Z} \cong [0,1)$ with $M$ i.i.d uniform on $[0,1]$ random variables $U_{1}^{(1)}, \dots, U_{1}^{(m_1)}$ , …, $U_{n}^{(1)}, \dots, U_{n}^{(m_n)}$ and let $U_{1:M} \lt \cdots \lt U_{M:M}$ be their order statistics. Starting from $0$ we walk around the clock until we encounter the first of the variables $U_{1}^{(i)}$ at some random index $I_1$ . We continue from the random index $I_1$ until we encounter the first of the variables $U_{2}^{(i)}$ (circling back if necessary) and continue like this until we encounter the first of the variables $U_{n}^{(i)}$ . We then obtain the random sequence $(I_1, I_2, \dots, I_n)$ and $D_{n}$ is the number of times we circled around the clock. Finally, let us denote by $(X_1, \dots, X_n)$ the lengths (clockwise) of the segments $[U_{I_1:M}, U_{I_2:M}]$ , $\dots$ , $[U_{I_{n-1}:M}, U_{I_{n}:M}]$ , $ [U_{I_{n}:M}, U_{I_{1}:M}]$ on the clock. The model described in Section 4 is the particular instance of this model where $m_1 = \dots = m_n = 2$ .

Remark 5.1. When there is no risk of confusion, we shall suppress the parameters $m_1, \dots, m_n$ to simplify the notation.

Proposition 5.2. The following hold

1. 1. The random lengths $X_1, X_2, \dots, X_n$ are independent random variables and $X_i$ has distribution beta( $1,m_i$ ) for each $ 1 \leq i \leq n$ .

2. 2. The random sequence of indices $(I_1, I_2, \dots, I_n)$ is independent of the order statistics $(U_{1:M} \lt \cdots \lt U_{M:M})$ .

Proof. Notice that $X_1 = \min (U_1^{(1)}, \dots, U_1^{(m_1)})$ is a beta( $1,m_1$ ) random variable. Also, since $U_2^{(1)}, \dots, U_2^{(m_2)}$ are i.i.d uniform and are independent of the position of $X_1$ on the circle, the variables $U_2^{(i)} - X_1 \mod \mathbb{Z} \in [0,1)$ are still i.i.d uniform so $X_2$ is also beta( $1,m_2$ ) and independent of $X_1$ . Running the same argument repeatedly we deduce that the variables $X_1, X_2 \dots, X_n$ are independent with $X_i \sim \textrm{beta}(1,m_i)$ . Also, the random index $I_n$ at which the process stops depends only on the relative positions of the variables $U_{1}^{(1)}, \dots, U_{1}^{(m_1)}$ , …, $U_{n}^{(1)}, \dots, U_{n}^{(m_n)}$ i.e. $I_n$ is fully determined by the random permutation of $\{1,\dots, M\}$ induced by the $M$ i.i.d uniforms. We then deduce that $I_n$ is independent of the order statistics $(U_{1:M} \lt U_{2:M} \lt \cdots \lt U_{M:M})$ .

The number $D_{n}$ of turns around the clock can also be expressed as follows

(5.1) \begin{equation} D_{n} = \lfloor S_{n} \rfloor, \quad \text{ where } S_{n} \,:\!=\, X_1 + \dots + X_n. \end{equation}

Let us denote by $L_n = L(m_1, m_2, \dots, m_n)$ the length of the longest continuous increasing subsequence of $\tau _n$ starting with $1$ ; that is the largest integer $1\leq \ell \leq n$ such that

\begin{equation*} 1,2,3,\dots, \ell \quad \text { is a subsequence of }\tau _n. \end{equation*}

Example 5.3. Suppose $n = 4$ and $(m_1,m_2,m_3,m_4) = (2,3,2,4)$ and consider the permutation $\tau _n = ({1},4,4,1,4,{2 },4,{3},3,2,2)$ . The the longest increasing continuous subsequence of $\tau _n$ starting from $1$ (the boldfaced subsequence) has length $L_4 = 3$ in this case.

For an infinite sequence $m = (m_1,m_2, \dots )$ of positive integers, notice that we can construct the sequences of variables $L_n = L(m_1,\dots, m_n)$ , $D_n = D(m_1,\dots, m_n)$ and $I_n = I(m_1, \dots, m_n)$ on a common probability space. This is done by marking an additional $m_n$ i.i.d uniform positions on the circle $\mathbb{T}$ at each step $n$ . Notice then that $(L_n = L(m_1, \dots, m_n))_{n \geq 1}$ is an increasing sequence of random variables so we define

\begin{equation*} L_{\infty } \,:\!=\, \lim \limits _{n \to \infty } L_n \quad \text {and} \quad \mathcal {L}_m \,:\!=\, \mathbb {E}[L_\infty ]. \end{equation*}

Proposition 5.4. We have the following

\begin{equation*} L_{n} = \sum _{ k = 0 }^{n} 1[S_k \leq 1] \quad \text {and} \quad L_{\infty } = \sum _{k = 0}^{\infty } 1[S_k \leq 1]. \end{equation*}

In particular, we have $(L_n = n) = (D_n = 0)$ and for $n \geq k$ we have

\begin{equation*} ( L(m_1, \dots, m_n) \geq k ) = (L(m_1, \dots, m_k) = k). \end{equation*}

Proof. The length $L_n$ of the longest sequence of the form $1 \dots \ell$ is the maximal integer $\ell$ such that $S_\ell \leq 1$ , i.e. the maximal $l$ such that the random walk $(S_k)_{k\geq 0}$ does not shoot over $1$ . Then we deduce that indeed

\begin{equation*} L_{n} = \sum _{ k = 0 }^{n} 1[S_k \leq 1]. \end{equation*}

The rest of the statements follow immediately from this equation.

Corollary 5.5. For $k \leq n$ we have

\begin{equation*} {\mathbb {P}}(L_n \geq k) = {\mathbb {P}}(S_{k} \leq 1). \end{equation*}

Proof. Follows immediately from Proposition 5.4.

Remark 5.6. When $m_1 = m_2 = \dots m_n = 1$ , the random variable $S_n$ is the sum of $n$ i.i.d uniform random variables on $[0,1]$ and the fractional part $S_n^\circ$ has uniform distribution on $\mathbb{T}$ . The index $I_n$ has uniform distribution in $\{1,\dots, n\}$ and the distribution of the number of descents

\begin{equation*}P(D_n = k) = \frac {A_{n,k}}{n!}, \quad (0 \leq k \leq n-1)\end{equation*}

is given by the Eulerian numbers $A_{n,k}$ , see [37, Section 1.4].

Horton and Kurn [18, Theorem and Corollary (c)] gives a formula for the number of permutations $\tau$ of the multiset $1^{m_1}2^{m_2}\dots n^{m_n}$ for which $L_n = n$ ; that is a formula for

\begin{equation*} \frac {M!}{m_1! \dots m_n!} \ {\mathbb {P}}(L_n = n). \end{equation*}

We shall interpret this formula in our context and rederive it from a probabilistic perspective.

Theorem 5.7. The number of permutations $\tau _n$ of the multiset $1^{m_1} 2 ^{m_2} \dots n^{m_n}$ that contain the sequence $(1,2,\dots,n)$ is given by

(5.2) \begin{equation} \frac{M!}{m_1! \dots m_n!}{\mathbb{P}}(L_n = n) = ({-}1)^M \sum _{j = 0}^{M} \binom{M}{j} \frac{c_{j}}{j!}, \end{equation}

where

\begin{equation*} c_j = ({-}1)^n [\theta ^j] \prod _{i = 1}^{n} E_{m_i - 1}({-} \theta ), \end{equation*}

with $[x^n] f(x)$ denoting the coefficient of $x^n$ in the power series expansion of $f$ .

Proof. Similarly to our discussion in Section 3, we can obtain an expression for ${\mathbb{P}}(S_{n} \leq x)$ by inverting the Laplace transform of $S_{n}$ . First recall that the Laplace transform of $X_i \sim \textrm{beta}(1,m_i)$ is

\begin{equation*} \varphi _{X_i}(\theta ) = \mathbb {E}[ e^{- \theta X_i }] = ({-}1)^{m_i} \frac {m_i!}{\theta ^{m_i}} \left ( e^{-\theta } - E_{m_i - 1}({-} \theta ) \right ), \end{equation*}

where $E_k(x)$ denotes the exponential polynomial $E_k(x) = \sum \limits _{i = 0}^{k} x^i/i!$ . So the Laplace transform of $S_{n}$ is then given by

\begin{equation*} \varphi _{S_{n}}(\theta ) = \frac {({-}1)^M \prod \limits _{i=1}^{n} m_i !} {\theta ^M} \prod _{i = 1}^{n} \left ( e^{-\theta } - E_{m_i - 1}({-}\theta )\right ). \end{equation*}

Using (3.10) to invert this Laplace transform, we get

\begin{equation*} {\mathbb {P}}(S_{n} \leq x) = ({-}1)^M \left (\prod \limits _{i=1}^{n} m_i ! \right ) \sum _{k, j \geq 0} \alpha _{k,j} \frac {(x-k)^{M-j}_+ }{(M-j)!}, \end{equation*}

where $\alpha _{k,j}$ is the coefficient of $\theta ^j X^k$ in the polynomial $\prod _{i=1}^n (X - E_{m_i - 1}({-}\theta ))$ . So we deduce that

\begin{equation*} {\mathbb {P}}(L_n = n) = {\mathbb {P}}(S_n \leq 1) = ({-}1)^M \left (\prod \limits _{i=1}^{n} m_i ! \right ) \sum _{j = 0}^{M} \frac {c_{j}}{(M-j)!}, \end{equation*}

with

\begin{equation*} c_j = \alpha _{0,j} = ({-}1)^n [\theta ^j] \left ( \prod _{i = 1}^{n} E_{m_i - 1}({-} \theta ) \right ). \end{equation*}

Multiplying by $ M!/ (m_1! \dots m_n!)$ we get the formula (5.2).

We suppose from now on that $m \,:\!=\, m_1 = m_2 = \dots \geq 1$ . Let $\mathcal{L}_{n,m}$ and $\mathcal{L}_{m}$ denote the expectation of $L_n$ and $L_\infty$ ; that is

\begin{equation*} \mathcal {L}_{n,m} \,:\!=\, \mathbb {E}[L_n] \quad \text {and} \quad \mathcal {L}_{m} \,:\!=\, \lim _{n \to \infty } \mathcal {L}_{n,m} = \mathbb {E}[L_{\infty }]. \end{equation*}

In [8], the authors present a fine asymptotic study of $\mathcal{L}_{m}$ as $m \to \infty$ . In this paper, we provide a pleasant probabilistic framework in which the discussion [8] fits rather naturally.

Let $(N(t), t \geq 0)$ be the renewal process with beta( $1,m$ )-distributed i.i.d jumps $X_i$ i.e.

\begin{equation*} N(t) = \sum _{n \geq 1}^{\infty } 1[S_n \leq t]. \end{equation*}

Notice that, by virtue of Proposition 5.4, the variable $N(1) = L_\infty - 1$ is the number of renewals of $N$ in $[0,1]$ . Let $M(t) \,:\!=\, \mathbb{E}[N(t)]$ denote the mean of $N(t)$ . By first step analysis, $M(t)$ satisfies the following equation for $t \in [0,1]$ :

(5.3) \begin{align} M(t) &={\mathbb{P}}(X_1 \leq t) + m \int _{0}^{t} M(t-x) (1-x)^{m-1} dx, \\[3pt] &={\mathbb{P}}(X_1 \leq t) + m \int _{0}^{t} M(x) (1 - t + x)^{m-1} dx. \nonumber \end{align}

From (5.3) we can deduce that $M$ satisfies the following differential equation

(5.4) \begin{equation} 1 + \sum _{k = 0}^{m} \frac{({-}1)^{k}}{k!} M^{(k)}(t) = 0. \end{equation}

Theorem 5.8. Let $\alpha _1, \dots, \alpha _m$ be the $m$ distinct complex roots of the exponential polynomial $E_m(x) = \sum _{k = 0}^{m} x^k/k!$ . Then the mean function $M(t)$ is given by

(5.5) \begin{equation} M(t) = - 1 - \sum _{k= 1}^{m} \alpha _k^{-1} e^{-\alpha _k t}. \end{equation}

Before we prove Theorem 5.8, we first recall a couple of intermediate results.

Lemma 5.9. Let $z$ be a non-zero complex number. Then, for any positive integer $n$ and $t \in [0,1]$ , we have the following:

\begin{equation*} \int _{0}^{t} e^{z x} (1-x)^{n} dx = n! \sum _{j = 0}^{n} \frac { e^{zt}(1-t)^j - 1}{j!} z^{j-n-1}. \end{equation*}

Proof. Follows immediately by induction on $n$ and integration by parts.

The following lemma is an adaptation of [40, Theorem 7].

Lemma 5.10. Let $\alpha _1, \dots, \alpha _m$ be the $m$ distinct complex zeros of $E_m(x)$ . Then we have the following

\begin{equation*} \sum _{k = 1}^{m} \alpha _k^{-j} = \begin {cases} -1, \quad &\text {if } j = 1,\\[3pt] 0, \quad &\text {if } 2 \leq j \leq m,\\[3pt] 1/m!, \quad &\text {if } j = m+1. \end {cases} \end{equation*}

Proof of Theorem 5.8. The mean function $M(t)$ satisfies (5.4). The latter is an order $m$ ODE with constant coefficients and its characteristic polynomial is $E_m({-}x)$ whose roots are $-\alpha _1, \dots, - \alpha _m$ . So the solution is of the form

\begin{equation*} M(t) = -1 + \sum _{k = 1}^{m} \beta _k e^{-\alpha _k t}. \end{equation*}

Setting $\beta _k = - \alpha _k^{-1}$ for $1 \leq k \leq m$ , it suffices to show that $M(t)$ satisfies (5.3). To that end notice that, thanks to Lemma 5.9, we have

\begin{align*} &{\mathbb{P}}(X_1 \leq t) + m \int _{0}^{t} M(t-x) (1-x)^{m-1} dx\\[3pt] &\quad= m \int _{0}^{t} (1+M(t-x)) (1-x)^{m-1} dx\\[3pt] &\quad= - \sum _{k = 1}^{m} m \alpha _k^{-1} \int _{0}^{t} e^{-\alpha _k (t-x)} (1-x)^{m-1} dx \\[3pt] &\quad= - \sum _{k = 1}^{m} m \alpha _k^{-1} e^{-\alpha _k t} \int _{0}^{t} e^{\alpha _k x} (1-x)^{m-1} dx \\[3pt] &\quad= \sum _{k = 1}^{m} m \alpha _k^{-1} e^{-\alpha _k t} (m-1)! \sum _{j = 0}^{m-1} \frac{1 - e^{\alpha _k t}(1-t)^j}{j!} \alpha _k^{j - m}\\[3pt] &\quad= m! \sum _{k = 1}^{m} \sum _{j = 0}^{m-1} \frac{e^{-\alpha _k t} - (1-t)^j}{j!} \alpha _k^{j-m-1}. \end{align*}

Now notice that, thanks to Lemma 5.10, we have

\begin{equation*} \sum _{j=0}^{m-1} \sum _{k=1}^{m} \frac {(1-t)^j}{j!} \alpha _k^{j-m-1} = \sum _{k=1}^{m} \alpha _k^{-m-1} = \frac {1}{m!}. \end{equation*}

We also have

\begin{equation*} \sum _{k=1}^{m} \sum _{j=0}^{m-1} \frac {e^{-\alpha _k t}}{j!} \alpha _k^{j-m-1} = \sum _{k=1}^{m} \alpha _k^{-m-1} e^{-\alpha _k t} \sum _{j=0}^{m-1} \frac {\alpha ^j}{j!} = - \frac {1}{m!} \sum _{k=1}^{m} \alpha _k^{-1} e^{-\alpha _k t}. \end{equation*}

The last equation follows from the fact that $\alpha _k$ is a zero of $E_m(x) = \sum _{j = 0}^{m} x^j/ j!$ . So combining the last two equations with the previous one, we get

\begin{equation*} {\mathbb {P}}(X_1 \leq t) + m \int _{0}^{t} M(t-x) (1-x)^{m-1} dx = - 1 - \sum _{k=1}^{m} \alpha _k^{-1} e^{-\alpha _k t} = M(t). \end{equation*}

Corollary 5.11 (Theorem 1.1-(a) in [8]). The expectation $\mathcal{L}_{m}$ is given by

\begin{equation*} \mathcal {L}_{m} = \sum _{k = 1}^{m} - \alpha _k^{-1} e^{ - \alpha _k}. \end{equation*}

In particular we have

\begin{equation*} \mathcal {L}_2 = e(\cos\!(1) + \sin\! (1)). \end{equation*}

Proof. Since $L_\infty = 1 + N(1)$ , we deduce that $\mathcal{L}_{m} = 1 + M(1)$ and the result follows immediately from Theorem 5.8.

Remark 5.12. Note that derivatives of $M$ at $0$ are the moments of the roots $\alpha _1, \dots, \alpha _m$ i.e.

\begin{equation*} \mu (j,m) \,:\!=\, \sum _{k=1}^{m} \alpha _k^{j} = ({-}1)^j M^{(j+1)}(0), \quad \text {for } j \geq 0. \end{equation*}

The functional equation (5.3) then gives a recursion that these moments satisfy:

\begin{equation*} \mu ({-}1,m) = 0 \quad \text {and} \quad \mu (j,m) = (m)_{j+1} - \sum _{i = 0}^{j-1} \ (m)_{i+1} \mu (j-i-1,m), \quad \text {for } j \geq 0. \end{equation*}

where $(X)_k = X(X-1)\dots (X-k+1)$ is the $k$ th falling factorial polynomial. These moments are polynomials $\mu (j,\cdot )$ in $m$ and it would be interesting to give an expression for $\mu (j,X)$ and study its properties as suggested in [40].

To conclude this section, we give a positive answer to Conjectures 4.1 and 4.2 of [8]. For any integer $m \geq 1$ , let $X_1^{(m)}, X_2^{(m)}, \dots$ be a sequence of i.i.d random variables with beta( $1,m$ ) distribution and denote by $L_{n,m}$ and $L_{\infty, m}$ the following random variables

\begin{equation*} L_{n,m} = \sum _{k = 1}^{n} 1\left [S^{(m)}_k \leq 1\right ] \quad \text {and} \quad L_{\infty, m} = \sum _{k = 1}^{\infty } 1\left [S^{(m)}_k \leq 1\right ], \end{equation*}

with

\begin{equation*} S^{(m)}_n = X_1^{(m)} + \dots + X_n^{(m)}, \quad \text {for } n \geq 1. \end{equation*}

Proposition 5.13. The random variable $(L_{\infty, m} - m)/ \sqrt{m}$ converges in distribution to a Gaussian measure with mean $0$ and variance $1$ .

Proof. For $m \geq 1$ and $x \in{\mathbb{R}}$ let $u(x,m) \,:\!=\, \lfloor m + x \sqrt{m} \rfloor$ . We then have

\begin{align*}{\mathbb{P}}\left ( \frac{L_{\infty, m} - m}{\sqrt{m}} \leq x \right ) &={\mathbb{P}}\left (L_{\infty, m} \leq m + x\sqrt{m}\right )\\[3pt] &={\mathbb{P}}\left (L_{\infty, m} \leq u(x,m) \right )\\[3pt] &={\mathbb{P}}\left (S_{u(x,m) + 1} \gt 1 \right )\\[3pt] &={\mathbb{P}}\left ( \frac{ m S_{u(x,m) + 1} - u(x,m) }{\sqrt{u(x,m)}} \gt \frac{ m - u(x,m)}{\sqrt{u(x,m)}} \right ). \end{align*}

Denote by $(Y_{k,m})$ the array defined as follows:

\begin{equation*} Y_{k,m} = \frac {1}{\sqrt {m}} (m X_k^{(m)} - 1), \quad \text {for } k, m \geq 1. \end{equation*}

We then have $\mathbb{E}[Y_{k,m}] = 0$ and this array satisfies the conditions for the Lindeberg-Feller theorem [13, Theorem 3.4.10], see Section B. Applying this theorem yields

\begin{equation*} Y_{m,1} + \dots + Y_{m, m} \xrightarrow [m \uparrow \infty ]{} \mathcal {N}(0,1), \end{equation*}

but since $m - u(x,m) \sim x \sqrt{m}$ as $m \uparrow \infty$ we also deduce that

\begin{equation*} Y_{m,1} + \dots + Y_{m, u(x,m)} \xrightarrow [m \uparrow \infty ]{} \mathcal {N}(0,1). \end{equation*}

To conclude, notice that:

\begin{equation*} \frac { m S_{u(x,m) + 1} - u(x,m) }{\sqrt {u(x,m)}} = \sqrt { \frac {m}{u(x,m)} } \left ( Y_{m,1} + \dots + Y_{m, u(x,m)} \right ) \to \mathcal {N}(0,1) \quad \text {as } m \uparrow \infty . \end{equation*}

and

\begin{equation*} \frac {m - u(x,m)}{\sqrt {u(x,m)}} \to -x \quad \text {as } m \uparrow \infty . \end{equation*}

So we deduce:

\begin{equation*} {\mathbb {P}}\left ( \frac {L_{\infty, m} - m}{\sqrt {m}} \leq x \right ) \to \int _{-x}^{\infty } \frac {1}{\sqrt {2\pi }} e^{-u^2/2} du = \int _{- \infty }^{x} \frac {1}{\sqrt {2\pi }} e^{-u^2/2} du, \quad \text {as } m \uparrow \infty \end{equation*}

6. Wrapping probability distributions on the circle

In the decomposition (1.14) for an exponentially distributed $X = \gamma _1/\lambda$ with parameter $\lambda \gt 0$ ; that is

\begin{equation*} {\mathbb {P}}(X \gt t) = e^{- \lambda t}, \quad \text {for } t \geq 0, \end{equation*}

the Eulerian generating function (1.12) is the probability density of the fractional part $(\gamma _1/\lambda )^\circ$ at $u \in [0,1)$ . In this probabilistic representation of Euler’s exponential generating function (1.3), the factorially normalised Bernoulli polynomials $b_n(u)$ for $n\gt 0$ are the densities at $u \in [0,1)$ of a sequence of signed measures on $[0,1)$ , each with total mass $0$ , which when weighted by $({-}\lambda )^n$ and summed over $n \gt 0$ give the difference between the probability density of $(\gamma _1/\lambda )^\circ$ and the uniform probability density $b_0(u) \equiv 1$ for $u \in [0,1)$ .

For a positive integer $r$ and a positive real number $\lambda$ , let $f_{r,\lambda }$ denote the probability density of the gamma( $r,\lambda$ ) distribution:

\begin{equation*} f_{\gamma _{r,\lambda }}(x) = \frac {\lambda ^r}{\Gamma (r)} e^{-\lambda x} x^{r - 1} 1_{x \gt 0}, \quad x \in {\mathbb {R}}. \end{equation*}

It is well known that $f_{r,\lambda }$ is the $r$ -fold convolution of $f_{1,\lambda }$ on the real line i.e. $f_{\gamma _{r,\lambda }} = (f_{\gamma _{1,\lambda }})^{ \ast r}$ .

Let $\gamma _{r,\lambda }$ be a random variable with distribution gamma( $r,\lambda$ ) and let us denote by $\gamma _{r,\lambda }^\circ$ the random variable $\gamma _{r,\lambda } \mod \mathbb{Z}$ on the circle $\mathbb{T}$ . The probability density of $\gamma _{r,\lambda }^\circ$ on ${\mathbb{T}} = [0,1)$ is given for $0 \le u \lt 1$ by

(6.1) \begin{equation} f_{\gamma _{r,\lambda }}^\circ (u) = \sum _{m \in \mathbb{Z}}^{} f_{\gamma _{r,\lambda }}(u + m) = \frac{\lambda ^r}{\Gamma (r)} e^{-\lambda u} \sum _{m = 0 }^{\infty } (u+m)^{r-1} e^{-\lambda m} \end{equation}

(6.2) \begin{equation} = \frac{\lambda ^r}{\Gamma (r)} e^{-\lambda u } \Phi (e^{-\lambda }, 1 -r, u), \end{equation}

where $\Phi$ is the Hurwitz-Lerch zeta function $\Phi (z,s,u) = \sum _{m \geq 0} \frac{z^m}{(u + m)^s}$ . In particular, for $r = 1$ the probability density of $\gamma _{1,\lambda }^\circ$ , the fractional part of an exponential variable with mean $1/\lambda$ , at $u \in [0,1)$ , is

\begin{equation*} f_{\gamma _{1,\lambda }}^\circ (u) = \frac {\lambda e^{\lambda (1-u)}}{e^{\lambda } - 1} = B(1-u,\lambda ) = 1 + \sum _{n = 1}^{\infty } b_n(1-u) \lambda ^n \end{equation*}

where $B(x,\lambda )$ , evaluated here for $x = 1-u$ , is the generating function in (1.3). Combined with the reflection symmetry (1.11), this shows that the probability density of $\gamma _{1,\lambda }^\circ$ can be expanded in Bernoulli polynomials as:

(6.3) \begin{equation} f_{\gamma _{1,\lambda }}^\circ (u) = 1 + \sum _{n = 1}^{\infty } ({-}1)^n b_n(u) \lambda ^n \qquad (0 \leq u \lt 1 ). \end{equation}

The following proposition generalises this result to all integers $r \geq 1$ .

The expansion (6.4) can be read from (6.2) and formula (11) on page 30 of [15]. The consequent interpretation (6.5) of $b_r(u)$ for $r \gt 0$ , as the density of a signed measure describing how the probability density $f_{\gamma _{r,\lambda }}^\circ (u)$ approaches the uniform density $1$ as $\lambda \downarrow 0$ , dates back to the work of Nörlund [32, p. 53], who gave an entirely analytical account of this result. See also [9] for further study of the wrapped gamma and related probability distributions, and [12] for various identities related to (6.4).

Proposition 6.1 (Wrapped gamma distribution). For each $r = 1,2,3, \ldots$ the wrapped gamma density admits the following expansion:

(6.4) \begin{equation} f_{\gamma _{r,\lambda }}^\circ (u) = 1 + \sum _{n=r}^{\infty } ({-}1)^{n-r+1} \binom{n-1}{r-1} b_n(u) \lambda ^n \quad \text{ for } 0 \lt \lambda \lt 2 \pi \end{equation}

where the convergence is uniform in $u \in [0,1)$ . In particular, as $\lambda \downarrow 0$

(6.5) \begin{equation} f_{\gamma _{r,\lambda }}^\circ (u) = 1 - \lambda ^r b_r(u) + O\left(\lambda ^{r+1}\right), \quad \textrm{ uniformly in } u \in [0,1). \end{equation}

Proof. Since $f_{\gamma _{r,\lambda }} = (f_{\gamma _{1,\lambda }})^{ \circledast r}$ we deduce that $f_{\gamma _{r,\lambda }}^\circ = (f_{\gamma _{1,\lambda }}^\circ )^{\circledast r}$ . Then, combining (6.3) and Corollary 1.2 we deduce that

\begin{align*} f_{\gamma _{r,\lambda }}^\circ (u) &= \left(\underbrace{ f_{\gamma _{1,\lambda }}^\circ \circledast \dots \circledast f_{\gamma _{1,\lambda }}^\circ }_{r \textrm{ factors}}\right)(u)\\[3pt] &= 1 + \sum _{k_1,\dots, k_r \geq 1} ({-}1) ^{k_1 + \dots + k_r}\lambda ^{k_1 + \dots + k_r} \left(b_{k_1} \circledast \dots \circledast b_{k_r}\right)(u)\\[3pt] &= 1 + \sum _{n = r}^{\infty } \sum _{ \substack{ k_1,\dots,k_r \geq 1 \\[3pt] k_1+\dots + k_r = n } }^{} ({-}1)^n \lambda ^n ({-}1)^{-r+1 }b_{n}(u)\\[3pt] &= 1+ \sum _{n = r}^{\infty } ({-}1)^{n-r+1} A_{r,n} \lambda ^n b_{n}(u), \end{align*}

where $A_{r,n} = \binom{n-1}{r-1}$ is the number of $r$ -tuples of positive integers that sum to $n$ . Notice that all the sums we considered are summable uniformly in $u \in [0,1]$ since $\left \lVert b_n\right \rVert _\infty = O((2\pi )^n)$ as $n \to \infty$ , see (1.7).

Remark 6.2. The general problem of expanding a function on $\mathbb{T}$ as a sum of Bernoulli polynomials was first treated Jordan [21, Section 85] and Mordell [31]. In our context, we think of the expansion of a function in Bernoulli polynomials as an analogue of the Taylor expansion where we work with the convolutions $\circledast$ instead of the usual multiplication of functions; i.e. we view expansions of the form

\begin{equation*} f(x) = a_0(f) + \sum _{n = 1}^{\infty } ({-}1)^{n-1} a_{n}(f) b_1^{\circledast n} (x) = a_0(f) + \sum _{n = 1}^{\infty } a_{n}(f) b_n(x), \end{equation*}

as an analogue of Taylor expansions

\begin{equation*} f(x) = f(0) + \sum _{n=1}^{\infty } \frac {f^{(n)}(0)}{n!} x^n. \end{equation*}

As we have seen in this section, this point of view is especially fruitful when one wishes to convolve probability measures on ${\mathbb{T}} = [0,1)$ . If $f$ is a $C^\infty$ function on $[0,1]$ satisfying some dominance condition (see [31, Theorem 1]), the coefficient of $b_1^{\circledast }(x)$ in the expansion of $f$ is given by

\begin{equation*} ({-}1)^{n-1} a_n(f) = (f^{(n-1)}(1) - f^{(n-1)}(0)), \quad \text {for } n \geq 0. \end{equation*}