We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We prove that any continuous function can be locally approximated at a fixed point
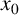$x_{0}$
by an uncountable family resistant to disruptions by the family of continuous functions for which
$x_{0}$
is a fixed point. In that context, we also consider the property of quasicontinuity.
