No CrossRef data available.
Article contents
QUASICONTINUITY, NONATTRACTING POINTS, DISTRIBUTIVE CHAOS AND RESISTANCE TO DISRUPTIONS
Published online by Cambridge University Press: 06 October 2022
Abstract
We prove that any continuous function can be locally approximated at a fixed point 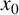 $x_{0}$ by an uncountable family resistant to disruptions by the family of continuous functions for which
$x_{0}$ by an uncountable family resistant to disruptions by the family of continuous functions for which  $x_{0}$ is a fixed point. In that context, we also consider the property of quasicontinuity.
$x_{0}$ is a fixed point. In that context, we also consider the property of quasicontinuity.
MSC classification
Primary:
26A18: Iteration
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 107 , Issue 1 , February 2023 , pp. 102 - 111
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
References
Cao, J. and McCluskey, A., ‘Topological transitivity in quasi-continuous dynamical systems’, Topology Appl. 301 (2021), Article no. 107496.CrossRefGoogle Scholar
Čiklová, M., ‘Dynamical systems generated by functions with connected
 ${G}_{\delta }$
graphs’, Real Anal. Exchange 30(2) (2005), 617–638.CrossRefGoogle Scholar
${G}_{\delta }$
graphs’, Real Anal. Exchange 30(2) (2005), 617–638.CrossRefGoogle Scholar
Crannel, A. and Martelli, M., ‘Dynamics of quasicontinuous systems’, J. Difference Equ. Appl. 6(3) (2000), 351–361.CrossRefGoogle Scholar
Devaney, R. L., An Introduction to Chaotic Dynamical Systems, 2nd edn (Addison-Wesley Publishing Company, Redwood City, CA, 1989).Google Scholar
Kempisty, S., ‘Sur les fonctions quasicontinues’, Fund. Math. 19(1) (1932), 184–197.CrossRefGoogle Scholar
Korczak-Kubiak, E., Loranty, A. and Pawlak, R. J., ‘On points focusing entropy’, Entropy 20(2) (2018), Article no. 128.CrossRefGoogle ScholarPubMed
Loranty, A. and Pawlak, R. J., ‘On the local aspects of distributional chaos’, Chaos 29(1) (2019), Article no. 013104.Google Scholar
Pawlak, H. and Pawlak, R. J., ‘The stable points and the attractors of Darboux functions’, Tatra Mt. Math. Publ. 40 (2008), 13–24.Google Scholar
Pawlak, H. and Pawlak, R. J., ‘Dynamics of Darboux functions’, Tatra Mt. Math. Publ. 42 (2009), 51–60.Google Scholar
Pawlak, R. J., ‘Distortion of dynamical systems in the context of focusing the chaos around the point’, Internat. J. Bifur. Chaos Appl. Sci. Engrg. 28(1) (2018), Article no. 1850006, 13 pages.CrossRefGoogle Scholar
Poprawa, J., Lokalne Aspekty Entropii i Chaosu Dyskretnych Układów Dynamicznych, Doctoral Thesis, Łódź, 2021.Google Scholar
Ruette, S., Chaos on the Interval—A Survey of Relationship Between the Various Kinds of Chaos for Continuous Interval Maps, University Lecture Series, 67 (American Mathematical Society, Providence, RI, 2017).Google Scholar
Schweizer, B. and Smítal, J., ‘Measures of chaos and a spectral decomposition of dynamical systems on the interval’, Trans. Amer. Math. Soc. 344(2) (1994), 737–754.CrossRefGoogle Scholar


