We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
It is proven that a conjecture of Tao (2010) holds true for log-concave random variables on the integers: For every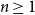 
$n \geq 1$, if 
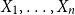$X_1,\ldots,X_n$ are i.i.d. integer-valued, log-concave random variables, thenas 
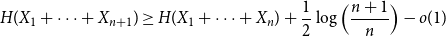\begin{equation*} H(X_1+\cdots +X_{n+1}) \geq H(X_1+\cdots +X_{n}) + \frac {1}{2}\log {\Bigl (\frac {n+1}{n}\Bigr )} - o(1) \end{equation*}
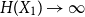$H(X_1) \to \infty$, where 
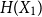$H(X_1)$ denotes the (discrete) Shannon entropy. The problem is reduced to the continuous setting by showing that if 
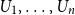$U_1,\ldots,U_n$ are independent continuous uniforms on 
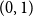$(0,1)$, thenas 
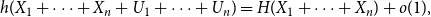\begin{equation*} h(X_1+\cdots +X_n + U_1+\cdots +U_n) = H(X_1+\cdots +X_n) + o(1), \end{equation*}
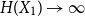$H(X_1) \to \infty$, where 
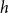$h$ stands for the differential entropy. Explicit bounds for the 
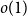$o(1)$-terms are provided.
We investigate additive properties of sets 
$A,$
where 
$A=\{a_1,a_2,\ldots ,a_k\}$
is a monotone increasing set of real numbers, and the differences of consecutive elements are all distinct. It is known that 
$|A+B|\geq c|A||B|^{1/2}$
for any finite set of numbers 
$B.$
The bound is tight up to the constant multiplier. We give a new proof to this result using bounds on crossing numbers of geometric graphs. We construct examples showing the limits of possible improvements. In particular, we show that there are arbitrarily large sets with different consecutive differences and sub-quadratic sumset size.
