Let $F$ be a non-archimedean local field of
residual characteristic different from $2$,
and let $G$ be a unitary, symplectic or orthogonal
group, considered as the fixed point subgroup in
$\tilde G={\rm GL}(N,F)$ of an involution $\sigma$.
We generalize the notion of a {\it simple character}
for $\tilde G$, which was introduced by Bushnell and
Kutzko [Annals of Mathematics Studies 129 (Princeton
University Press, 1993)], to define semisimple
characters.
Given a semisimple character $\theta$ for $\tilde G$
fixed by $\sigma$, we transfer it to a character
$\theta_{-}$ for $G$ and calculate its intertwining.
If the torus associated to $\theta_{-}$ is maximal
compact, we obtain supercuspidal representations of
$G$, which are new if the torus is split only over
a wildly ramified extension. 2000 Mathematics Subject Classification:
22E50.
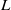 -packets
-packets