Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T14:10:36.172Z Has data issue: false hasContentIssue false
  • English
  • Français

Stable vectors in Moy–Prasad filtrations

Part of: Lie groups Linear algebraic groups and related topics Algebraic groups Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  09 February 2017

Jessica Fintzen  and
Beth Romano
Jessica Fintzen
Affiliation:
Department of Mathematics, Harvard University, One Oxford Street, Cambridge, MA 02138, USA email fintzen@umich.edu Current address: Department of Mathematics, University of Michigan, 2074 East Hall, 530 Church St, Ann Arbor, MI 48109, USA
Beth Romano
Affiliation:
Department of Mathematics, Boston College, 140 Commonwealth Avenue, Chestnut Hill, MA 02467, USA email blr24@dpmms.cam.ac.uk Current address: Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WB, UK
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 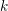$k$ be a finite extension of 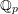$\mathbb{Q}_{p}$, let 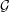${\mathcal{G}}$ be an absolutely simple split reductive group over 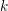$k$, and let 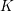$K$ be a maximal unramified extension of 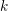$k$. To each point in the Bruhat–Tits building of 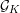${\mathcal{G}}_{K}$, Moy and Prasad have attached a filtration of ${\mathcal{G}}(K)$ by bounded subgroups. In this paper we give necessary and sufficient conditions for the dual of the first Moy–Prasad filtration quotient to contain stable vectors for the action of the reductive quotient. Our work extends earlier results by Reeder and Yu, who gave a classification in the case when 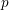$p$ is sufficiently large. By passing to a finite unramified extension of 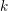$k$ if necessary, we obtain new supercuspidal representations of 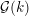${\mathcal{G}}(k)$.

Keywords

Moy–Prasad filtrationstable vectorssupercuspidal representations

MSC classification

Primary: 22E50: Representations of Lie and linear algebraic groups over local fields 20G25: Linear algebraic groups over local fields and their integers
Secondary: 11S37: Langlands-Weil conjectures, nonabelian class field theory 14L24: Geometric invariant theory
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 2 , February 2017 , pp. 358 - 372
Copyright
© The Authors 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, J. D., Refined anisotropic K-types and supercuspidal representations , Pacific J. Math. 185 (1998), 1–32.Google Scholar
Bruhat, F. and Tits, J., Groupes réductifs sur un corps local. II. Schémas en groupes. Existence d’une donnée radicielle valuée , Publ. Math. Inst. Hautes Études Sci. 60 (1984), 197–376.Google Scholar
Carter, R. W., Simple groups of Lie type, Wiley Classics Library (John Wiley, New York, 1989). Reprint of the 1972 original; MR 1013112 (90g:20001).Google Scholar
Griess, R. L. Jr, Elementary abelian p-subgroups of algebraic groups , Geom. Dedicata 39 (1991), 253–305, doi:10.1007/BF00150757; MR 1123145.Google Scholar
Gross, B. and Reeder, M., Arithmetic invariants of discrete Langlands parameters , Duke Math. J. 154 (2010), 431–508.Google Scholar
Hiraga, K., Ichino, A. and Ikeda, T., Formal degrees and adjoint 𝛾-factors , J. Amer. Math. Soc. 21 (2008), 283–304, doi:10.1090/S0894-0347-07-00567-X; MR 2350057.Google Scholar
Iwasawa, K., Local class field theory, Oxford Mathematical Monographs (Oxford Science Publications, The Clarendon Press–Oxford University Press, New York, 1986);MR 863740 (88b:11080).Google Scholar
Kaletha, T., Epipelagic L-packets and rectifying characters , Invent. Math. 202 (2015), 1–89, doi:10.1007/s00222-014-0566-4; MR 3402796.Google Scholar
Kim, J.-L., Supercuspidal representations: an exhaustion theorem , J. Amer. Math. Soc. 20 (2007), 273–320 (electronic), doi:10.1090/S0894-0347-06-00544-3; MR 2276772 (2008c:22014).Google Scholar
Moy, A. and Prasad, G., Unrefined minimal K-types for p-adic groups , Invent. Math. 116 (1994), 393–408.Google Scholar
Moy, A. and Prasad, G., Jacquet functors and unrefined minimal K-types , Comment. Math. Helv. 71 (1996), 98–121.CrossRefGoogle Scholar
Mumford, D., Geometric invariant theory, Ergebnisse der Mathematik und ihrer Grenzgebiete, Neue Folge, Band 34 (Springer, Berlin–New York, 1965); MR 0214602.CrossRefGoogle Scholar
Mumford, D., Stability of projective varieties , Enseign. Math. (2) 23 (1977), 39–110.Google Scholar
Reeder, M., Levy, P., Yu, J.-K. and Gross, B. H., Gradings of positive rank on simple Lie algebras , Transform. Groups 17 (2012), 1123–1190, doi:10.1007/s00031-012-9196-3; MR 3000483.Google Scholar
Reeder, M. and Yu, J.-K., Epipelagic representations and invariant theory , J. Amer. Math. Soc. 27 (2014), 437–477, doi:10.1090/S0894-0347-2013-00780-8; MR 3164986.CrossRefGoogle Scholar
Romano, B., On the local Langlands correspondence: new examples from the epipelagic zone, PhD thesis, Boston College (ProQuest LLC, Ann Arbor, MI, 2016); MR 3517860.Google Scholar
Tits, J., Reductive groups over local fields , Proc. Sympos. Pure Math. 33 (1979), 29–69.Google Scholar
Yu, J.-K., Construction of tame supercuspidal representations , J. Amer. Math. Soc. 14 (2001), 579–622 (electronic).Google Scholar