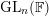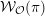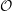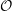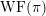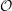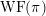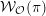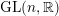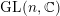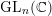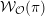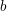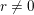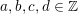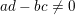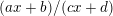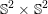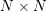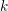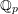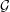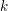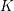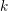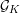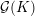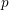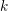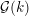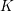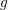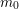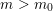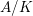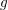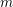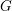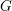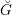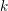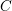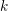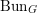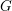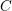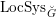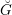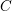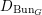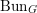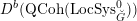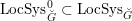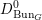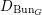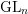We study generalized and degenerate Whittaker models for reductive groups over local fields of characteristic zero (archimedean or non-archimedean). Our main result is the construction of epimorphisms from the generalized Whittaker model corresponding to a nilpotent orbit to any degenerate Whittaker model corresponding to the same orbit, and to certain degenerate Whittaker models corresponding to bigger orbits. We also give choice-free definitions of generalized and degenerate Whittaker models. Finally, we explain how our methods imply analogous results for Whittaker–Fourier coefficients of automorphic representations. For 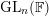\text{GL}_{n}(\mathbb{F})$\text{GL}_{n}(\mathbb{F})$ this implies that a smooth admissible representation \unicode[STIX]{x1D70B}$\unicode[STIX]{x1D70B}$ has a generalized Whittaker model 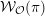{\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$ corresponding to a nilpotent coadjoint orbit 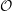{\mathcal{O}}${\mathcal{O}}$ if and only if 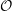{\mathcal{O}}${\mathcal{O}}$ lies in the (closure of) the wave-front set 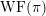\operatorname{WF}(\unicode[STIX]{x1D70B})$\operatorname{WF}(\unicode[STIX]{x1D70B})$. Previously this was only known to hold for 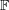\mathbb{F}$\mathbb{F}$ non-archimedean and 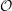{\mathcal{O}}${\mathcal{O}}$ maximal in 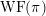\operatorname{WF}(\unicode[STIX]{x1D70B})$\operatorname{WF}(\unicode[STIX]{x1D70B})$, see Moeglin and Waldspurger [Modeles de Whittaker degeneres pour des groupes p-adiques, Math. Z. 196 (1987), 427–452]. We also express 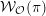{\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$ as an iteration of a version of the Bernstein–Zelevinsky derivatives [Bernstein and Zelevinsky, Induced representations of reductive p-adic groups. I., Ann. Sci. Éc. Norm. Supér. (4) 10 (1977), 441–472; Aizenbud et al., Derivatives for representations of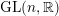\text{GL}(n,\mathbb{R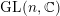})$\text{GL}(n,\mathbb{R})$and\text{GL}(n,\mathbb{C})$\text{GL}(n,\mathbb{C})$, Israel J. Math. 206 (2015), 1–38]. This enables us to extend to \text{GL}_{n}(\mathbb{R})$\text{GL}_{n}(\mathbb{R})$ and 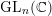\text{GL}_{n}(\mathbb{C})$\text{GL}_{n}(\mathbb{C})$ several further results by Moeglin and Waldspurger on the dimension of 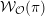{\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})${\mathcal{W}}_{{\mathcal{O}}}(\unicode[STIX]{x1D70B})$ and on the exactness of the generalized Whittaker functor.

We show that the finiteness of the fundamental groups of the smooth locus of lower dimensional log Fano pairs would imply the finiteness of the local fundamental group of Kawamata log terminal (klt) singularities. As an application, we verify that the local fundamental group of a three-dimensional klt singularity and the fundamental group of the smooth locus of a three-dimensional Fano variety with canonical singularities are always finite.

A seminal result due to Wall states that if x$x$ is normal to a given base b$b$, then so is rx+s$rx+s$ for any rational numbers r,s$r,s$ with r\neq 0$r\neq 0$. We show that a stronger result is true for normality with respect to the continued fraction expansion. In particular, suppose a,b,c,d\in \mathbb{Z}$a,b,c,d\in \mathbb{Z}$ with ad-bc\neq 0$ad-bc\neq 0$. Then if x$x$ is continued fraction normal, so is (ax+b)/(cx+d)$(ax+b)/(cx+d)$.

In this paper, we determine the group of contact transformations modulo contact isotopies for Legendrian circle bundles over closed surfaces of non-positive Euler characteristic. These results extend and correct those presented by the first author in a former work. The main ingredient we use is connectedness of certain spaces of embeddings of surfaces into contact 3-manifolds. This connectedness question is also studied for itself with a number of (hopefully instructive) examples.

A famous conjecture of Hopf states that \mathbb{S}^{2}\times \mathbb{S}^{2}$\mathbb{S}^{2}\times \mathbb{S}^{2}$ does not admit a Riemannian metric with positive sectional curvature. In this article, we prove that no manifold product N\times N$N\times N$ can carry a metric of positive sectional curvature admitting a certain degree of torus symmetry.

We develop a theory of commensurability of groups, of rings, and of modules. It allows us, in certain cases, to compare sizes of automorphism groups of modules, even when those are infinite. This work is motivated by the Cohen–Lenstra heuristics on class groups.

We prove the Green–Lazarsfeld secant conjecture [Green and Lazarsfeld, On the projective normality of complete linear series on an algebraic curve, Invent. Math. 83 (1986), 73–90; Conjecture (3.4)] for extremal line bundles on curves of arbitrary gonality, subject to explicit genericity assumptions.

Let k$k$ be a finite extension of \mathbb{Q}_{p}$\mathbb{Q}_{p}$, let {\mathcal{G}}${\mathcal{G}}$ be an absolutely simple split reductive group over k$k$, and let K$K$ be a maximal unramified extension of k$k$. To each point in the Bruhat–Tits building of {\mathcal{G}}_{K}${\mathcal{G}}_{K}$, Moy and Prasad have attached a filtration of {\mathcal{G}}(K)${\mathcal{G}}(K)$ by bounded subgroups. In this paper we give necessary and sufficient conditions for the dual of the first Moy–Prasad filtration quotient to contain stable vectors for the action of the reductive quotient. Our work extends earlier results by Reeder and Yu, who gave a classification in the case when p$p$ is sufficiently large. By passing to a finite unramified extension of k$k$ if necessary, we obtain new supercuspidal representations of {\mathcal{G}}(k)${\mathcal{G}}(k)$.

Assuming Vojta’s conjecture, and building on recent work of the authors, we prove that, for a fixed number field K$K$ and a positive integer g$g$, there is an integer m_{0}$m_{0}$ such that for any m>m_{0}$m>m_{0}$ there is no principally polarized abelian variety A/K$A/K$ of dimension g$g$ with full level-m$m$ structure. To this end, we develop a version of Vojta’s conjecture for Deligne–Mumford stacks, which we deduce from Vojta’s conjecture for schemes.

Let G$G$ be a semi-simple algebraic group over an algebraically closed field k$k$, whose characteristic is positive and does not divide the order of the Weyl group of G$G$, and let \breve{G}$\breve{G}$ be its Langlands dual group over k$k$. Let C$C$ be a smooth projective curve over k$k$ of genus at least two. Denote by \operatorname{Bun}_{G}$\operatorname{Bun}_{G}$ the moduli stack of G$G$-bundles on C$C$ and \operatorname{LocSys}_{\breve{G}}$\operatorname{LocSys}_{\breve{G}}$ the moduli stack of \breve{G}$\breve{G}$-local systems on C$C$. Let D_{\operatorname{Bun}_{G}}$D_{\operatorname{Bun}_{G}}$ be the sheaf of crystalline differential operators on \operatorname{Bun}_{G}$\operatorname{Bun}_{G}$. In this paper we construct an equivalence between the bounded derived category D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0}))$D^{b}(\operatorname{QCoh}(\operatorname{LocSys}_{\breve{G}}^{0}))$ of quasi-coherent sheaves on some open subset \operatorname{LocSys}_{\breve{G}}^{0}\subset \operatorname{LocSys}_{\breve{G}}$\operatorname{LocSys}_{\breve{G}}^{0}\subset \operatorname{LocSys}_{\breve{G}}$ and bounded derived category D^{b}(D_{\operatorname{Bun}_{G}}^{0}\text{-}\text{mod})$D^{b}(D_{\operatorname{Bun}_{G}}^{0}\text{-}\text{mod})$ of modules over some localization D_{\operatorname{Bun}_{G}}^{0}$D_{\operatorname{Bun}_{G}}^{0}$ of D_{\operatorname{Bun}_{G}}$D_{\operatorname{Bun}_{G}}$. This generalizes the work of Bezrukavnikov and Braverman in the \operatorname{GL}_{n}$\operatorname{GL}_{n}$ case.