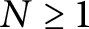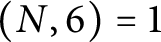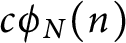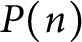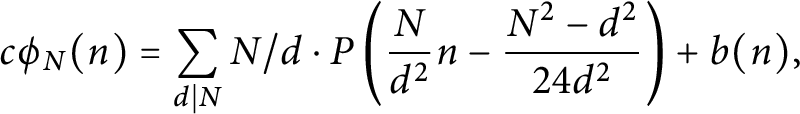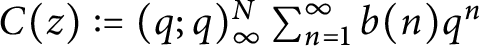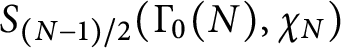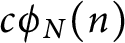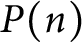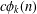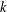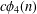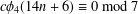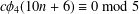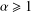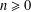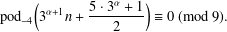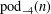Refine search
Actions for selected content:
16 results
Truncated versions of three identities of Euler and Gauss
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 30 August 2022, pp. 775-798
-
- Article
- Export citation
N-colored generalized Frobenius partitions: generalized Kolitsch identities
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 25 January 2022, pp. 447-469
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
11 - Knizhnik–Zamolodchikov-Type Equations, Selberg Integrals and Related Special Functions
-
-
- Book:
- Encyclopedia of Special Functions: The Askey-Bateman Project
- Published online:
- 30 September 2020
- Print publication:
- 15 October 2020, pp 368-401
-
- Chapter
- Export citation
VANISHING COEFFICIENTS IN QUOTIENTS OF THETA FUNCTIONS OF MODULUS FIVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 27 March 2020, pp. 387-398
- Print publication:
- December 2020
-
- Article
- Export citation
5 - Normal Forms for Kummer Surfaces
-
-
- Book:
- Integrable Systems and Algebraic Geometry
- Published online:
- 19 March 2020
- Print publication:
- 02 March 2020, pp 119-174
-
- Chapter
- Export citation
14 - Some Topological Applications of Theta Functions
-
-
- Book:
- Integrable Systems and Algebraic Geometry
- Published online:
- 19 March 2020
- Print publication:
- 02 March 2020, pp 440-484
-
- Chapter
- Export citation
CONGRUENCES MODULO 5 AND 7 FOR 4-COLORED GENERALIZED FROBENIUS PARTITIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 21 December 2016, pp. 157-176
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
Modular embeddings of Teichmüller curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 11 / November 2016
- Published online by Cambridge University Press:
- 21 September 2016, pp. 2269-2349
- Print publication:
- November 2016
-
- Article
- Export citation
ARITHMETIC PROPERTIES OF PARTITION QUADRUPLES WITH ODD PARTS DISTINCT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 08 July 2015, pp. 353-364
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Computing isogenies between abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 10 July 2012, pp. 1483-1515
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
INFINITE FAMILIES OF ARITHMETIC IDENTITIES FOR 4-CORES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 07 June 2012, pp. 304-315
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
Elliptic determinant evaluations and the Macdonald identities for affine root systems
-
- Journal:
- Compositio Mathematica / Volume 142 / Issue 4 / July 2006
- Published online by Cambridge University Press:
- 14 July 2006, pp. 937-961
- Print publication:
- July 2006
-
- Article
-
- You have access
- Export citation
Fourier invariant partially approximating subalgebras of the irrational rotation C*-algebra
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 88 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 08 March 2004, pp. 505-525
- Print publication:
- March 2004
-
- Article
- Export citation
The Vanishing of the Theta Function in the KP Direction: A Geometric Approach
-
- Journal:
- Compositio Mathematica / Volume 135 / Issue 3 / February 2003
- Published online by Cambridge University Press:
- 04 December 2007, pp. 323-330
- Print publication:
- February 2003
-
- Article
-
- You have access
- Export citation
Local heights on abelian varieties with split multiplicative reduction
-
- Journal:
- Compositio Mathematica / Volume 107 / Issue 3 / July 1997
- Published online by Cambridge University Press:
- 04 December 2007, pp. 289-317
- Print publication:
- July 1997
-
- Article
-
- You have access
- Export citation
An operational calculus for probability distributions via Laplace transforms
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 75-113
- Print publication:
- March 1996
-
- Article
- Export citation