Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T11:23:08.005Z Has data issue: false hasContentIssue false
  • English
  • Français

INFINITE FAMILIES OF ARITHMETIC IDENTITIES FOR 4-CORES

Part of: Additive number theory; partitions

Published online by Cambridge University Press:  07 June 2012

NAYANDEEP DEKA BARUAH  and
KALLOL NATH
NAYANDEEP DEKA BARUAH*
Affiliation:
Department of Mathematical Sciences, Tezpur University, Sonitpur, PIN-784028, India (email: nayan@tezu.ernet.in)
KALLOL NATH
Affiliation:
Department of Mathematical Sciences, Tezpur University, Sonitpur, PIN-784028, India (email: kallol08@tezu.ernet.in)
*
✉For correspondence; e-mail: nayan@tezu.ernet.in
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let u(n) and v(n) be the number of representations of a nonnegative integer n in the forms x2+4y2+4z2 and x2+2y2+2z2, respectively, with x,y,z∈ℤ, and let a4(n) and r3(n) be the number of 4-cores of n and the number of representations of n as a sum of three squares, respectively. By employing simple theta-function identities of Ramanujan, we prove that 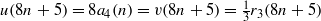$u(8n+5)=8a_4(n)=v(8n+5)=\frac {1}{3}r_3(8n+5)$. With the help of this and a classical result of Gauss, we find a simple proof of a result on a4 (n) proved earlier by K. Ono and L. Sze [‘4-core partitions and class numbers’, Acta Arith. 80 (1997), 249–272]. We also find some new infinite families of arithmetic relations involving a4 (n) .

Keywords

partitionst-corestheta functionsdissection

MSC classification

Secondary: 11P83: Partitions; congruences and congruential restrictions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 87 , Issue 2 , April 2013 , pp. 304 - 315
Copyright
Copyright © 2012 Australian Mathematical Publishing Association Inc.

References

[1]Berndt, B. C., Ramanujan’s Notebooks, Part III (Springer, New York, 1991).CrossRefGoogle Scholar
[2]Cooper, S. & Hirschhorn, M. D., ‘Results of Hurwitz type for three squares’, Discrete Math. 274 (2004), 9–24.CrossRefGoogle Scholar
[3]Garvan, F., Kim, D. & Stanton, D., ‘Cranks and t-cores’, Invent. Math. 101 (1990), 1–17.CrossRefGoogle Scholar
[4]Hirschhorn, M. D. & Sellers, J. A., ‘Two congruences involving 4-cores’, Electron. J. Combin. 3(2) (1996), R10.CrossRefGoogle Scholar
[5]Hirschhorn, M. D. & Sellers, J. A., ‘Some amazing facts about 4-cores’, J. Number Theory 60 (1996), 51–69.CrossRefGoogle Scholar
[6]Hirschhorn, M. D. & Sellers, J. A., ‘On representations of a number as a sum of three squares’, Discrete Math. 199 (1999), 85–101.CrossRefGoogle Scholar
[7]Ono, K. & Sze, L., ‘4-core partitions and class numbers’, Acta Arith. 80 (1997), 249–272.CrossRefGoogle Scholar