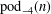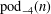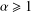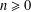Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kim, Byungchan
and
Toh, Pee Choon
2018.
On the Crank Function of Cubic Partition Pairs.
Annals of Combinatorics,
Vol. 22,
Issue. 4,
p.
803.
Tang, Dazhao
2025.
Internal Congruences Modulo Powers of 5 for Partition
k
-Tuples with Odd Parts Distinct
.
Experimental Mathematics,
Vol. 34,
Issue. 1,
p.
72.