Hostname: page-component-5b777bbd6c-v47t2 Total loading time: 0 Render date: 2025-06-18T19:33:59.975Z Has data issue: false hasContentIssue false
  • English
  • Français

Extremal behavior of stationary marked point processes

Part of: Geometric probability and stochastic geometry Stochastic processes

Published online by Cambridge University Press:  18 June 2025

Bojan Basrak ,
Ilya Molchanov  and
Hrvoje Planinić
Bojan Basrak*
Affiliation:
University of Zagreb
Ilya Molchanov*
Affiliation:
University of Bern
Hrvoje Planinić*
Affiliation:
University of Zagreb
*
*Postal address: Department of Mathematics, Faculty of Science, University of Zagreb, Bijenička cesta 30, 10000 Zagreb, Croatia.
***Institute of Mathematical Statistics and Actuarial Science, University of Bern, Alpeneggstr. 22, 3012 Bern, Switzerland. Email address: ilya.molchanov@stat.unibe.ch
*Postal address: Department of Mathematics, Faculty of Science, University of Zagreb, Bijenička cesta 30, 10000 Zagreb, Croatia.
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider stationary configurations of points in Euclidean space that are marked by positive random variables called scores. The scores are allowed to depend on the relative positions of other points and outside sources of randomness. Such models have been thoroughly studied in stochastic geometry, e.g. in the context of random tessellations or random geometric graphs. It turns out that in a neighborhood of a point with an extreme score it is possible to rescale positions and scores of nearby points to obtain a limiting point process, which we call the tail configuration. Under some assumptions on dependence between scores, this local limit determines the global asymptotics for extreme scores within increasing windows in 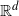$\mathbb{R}^d$. The main result establishes the convergence of rescaled positions and clusters of high scores to a Poisson cluster process, quantifying the idea of the Poisson clumping heuristic by Aldous (1989, in the point process setting). In contrast to the existing results, our framework allows for explicit calculation of essentially all extremal quantities related to the limiting behavior of extremes. We apply our results to models based on (marked) Poisson processes where the scores depend on the distance to the kth nearest neighbor and where scores are allowed to propagate through a random network of points depending on their locations.

Keywords

clusterextreme scoremarked point processmoving maximanearest neighborPoisson convergence

MSC classification

Primary: 60G70: Extreme value theory; extremal processes
Secondary: 60D05: Geometric probability and stochastic geometry 60G55: Point processes 60G57: Random measures
Type
Original Article
Information
Advances in Applied Probability , First View , pp. 1 - 42
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aldous, D. (1989). Probability Approximations via the Poisson Clumping Heuristic. Springer-Verlag, New York.10.1007/978-1-4757-6283-9CrossRefGoogle Scholar
Basrak, B. and Planinić, H. (2019). A note on vague convergence of measures. Statist. Probab. Lett. 153, 180–186.10.1016/j.spl.2019.06.004CrossRefGoogle Scholar
Basrak, B. and Planinić, H. (2021). Compound Poisson approximation for regularly varying fields with application to sequence alignment. Bernoulli 27, 1371–1408.10.3150/20-BEJ1278CrossRefGoogle Scholar
Basrak, B. and Segers, J. (2009). Regularly varying multivariate time series. Stochastic Process. Appl. 119, 1055–1080.10.1016/j.spa.2008.05.004CrossRefGoogle Scholar
Basrak, B., Planinić, H. and Soulier, P. (2018). An invariance principle for sums and record times of regularly varying stationary sequences. Probab. Theory Related Fields 172, 869–914.10.1007/s00440-017-0822-9CrossRefGoogle Scholar
Billingsley, P. (1968). Convergence of Probability Measures. New York, Wiley.Google Scholar
Bobrowski, O., Schulte, M. and Yogeshwaran, D. (2022). Poisson process approximation under stabilization and Palm coupling. Ann. H. Lebesgue 5, 1489–1534.10.5802/ahl.156CrossRefGoogle Scholar
Chenavier, N. and Otto, M. (2023). Compound Poisson process approximation under $\beta$ -mixing and stabilization. Technical report. arXiv math: 2310.15009.Google Scholar
Chenavier, N. and Robert, C. Y. (2018). Cluster size distributions of extreme values for the Poisson-Voronoi tessellation. Ann. Appl. Probab. 28, 3291–3323.10.1214/17-AAP1345CrossRefGoogle Scholar
Chiu, S. N., Stoyan, D., Kendall, W. S. and Mecke, J. (2013). Stochastic Geometry and Its Applications, 3rd edn. Wiley Series in Probability and Statistics. John Wiley & Sons, Ltd., Chichester.10.1002/9781118658222CrossRefGoogle Scholar
Daley, D. J. and Vere-Jones, D. (2003). An Introduction to the Theory of Point Processes, Vol. I, 2nd edn. Springer-Verlag, New York.Google Scholar
Daley, D. J. and Vere-Jones, D. (2008). An Introduction to the Theory of Point Processes, Vol. II, 2nd edn. Springer, New York.10.1007/978-0-387-49835-5CrossRefGoogle Scholar
Dombry, C., Hashorva, E. and Soulier, P. (2018). Tail measure and spectral tail process of regularly varying time series. Ann. Appl. Probab. 28, 3884–3921.10.1214/18-AAP1410CrossRefGoogle Scholar
Eichelsbacher, P., Raič, M. and Schreiber, T. (2015). Moderate deviations for stabilizing functionals in geometric probability. Ann. Inst. H. Poincaré Probab. Statist. 51, 89–128.10.1214/13-AIHP576CrossRefGoogle Scholar
Janßen, A. (2019). Spectral tail processes and max-stable approximations of multivariate regularly varying time series. Stochastic Process. Appl. 129, 1993–2009.10.1016/j.spa.2018.06.010CrossRefGoogle Scholar
Kallenberg, O. (2017). Random Measures, Theory and Applications. Springer, Cham.10.1007/978-3-319-41598-7CrossRefGoogle Scholar
Kulik, R. and Soulier, P. (2020). Heavy-Tailed Time Series. Springer, New York.10.1007/978-1-0716-0737-4CrossRefGoogle Scholar
Last, G. (2023). Tail processes and tail measures: an approach via Palm calculus. Extremes 26, 715–746.10.1007/s10687-023-00472-yCrossRefGoogle Scholar
Morariu-Patrichi, M. (2018). On the weak-hash metric for boundedly finite integer-valued measures. Bull. Aust. Math. Soc. 98, 265–276.10.1017/S0004972718000485CrossRefGoogle Scholar
Otto, M. (2025). Poisson approximation of Poisson-driven point processes and extreme values in stochastic geometry. Bernoulli 31, 30–54.10.3150/23-BEJ1688CrossRefGoogle Scholar
Owada, T. (2018). Limit theorems for Betti numbers of extreme sample clouds with application to persistence barcodes. Ann. Appl. Probab. 28, 2814–2854.10.1214/17-AAP1375CrossRefGoogle Scholar
Penrose, M. D. and Yukich, J. E. (2001). Central limit theorems for some graphs in computational geometry. Ann. Appl. Probab. 11, 1005–1041.10.1214/aoap/1015345393CrossRefGoogle Scholar
Planinić, H. (2019). Point processes in the analysis of dependent data. Doctoral Thesis. University of Zagreb.Google Scholar
Planinić, H. (2023). Palm theory for extremes of stationary regularly varying time series and random fields. Extremes 26, 45–82.10.1007/s10687-022-00447-5CrossRefGoogle Scholar
Pratt, J. W. (1960). On interchanging limits and integrals. Ann. Math. Statist. 31, 74–77.10.1214/aoms/1177705988CrossRefGoogle Scholar
Resnick, S. I. (2007). Heavy-Tail Phenomena. Springer, New York.Google Scholar
Schuhmacher, D. and Xia, A. (2008). A new metric between distributions of point processes. Adv. in Appl. Probab. 40, 651–672.10.1239/aap/1222868180CrossRefGoogle Scholar