Feeding potential and functional response of Oenopia sauzeti (Mulsant) against potato aphid, Macrosiphum euphorbiae Thomas (Hemiptera: Aphididae)

Abstract

Oenopia sauzeti (Mulsant) (Coccinellidae: Coleoptera) is a highly efficient predator of sap-sucking insect pests due to its high feeding capacity and broad prey range. The present investigation was carried out to find out the feeding potential and functional response of O. sauzeti fed on different densities of Macrosiphum euphorbiae (Thomas) (Aphididae: Hemiptera) nymphs in the in vitro condition with the overarching objective of appraising the ladybird beetle’s potential as a distinguished biological control agent. The newly emerged coccinellid grubs of a particular stage were reared individually on Petri plates with a known number of M. euphorbiae nymphs of a particular stage. The single individual of O. sauzeti consumed 1104.53, 936.53, 634.07, and 473.20 aphids in one generation when reared on the first, second, third, and fourth instars of M. euphorbiae, respectively. The female adult of predator recorded as a more voracious feeder compared to the male adult. O. sauzeti exhibits a type II functional response against potato aphid, and a significantly negative linear coefficient was obtained after logistic regression analysis for the proportion of prey consumed (N_a/N) as a function of initial prey density (N). The functional response parameters, i.e. attack rate and handling time, were estimated by applying Roger’s random predator equation. The attack rate increased, and handling time decreased with the advancement of the development stage of the predator. The voracious nature of both adults and grubs of the ladybird beetle makes this effective biocontrol agent to be used in the Integrated Pest Management Programme against the potato aphid.

Introduction

Coccinellids, commonly known as ladybird beetles, play a crucial role as potential biocontrol agents against various insect pests, particularly aphids, which are among the most damaging invertebrate pests affecting economically important crops (Boopathi et al., 2017; Dedryver et al., 2010; Michaud, 2012; Sarmento et al., 2007). As a part of pesticide-free management strategies, biological control, including augmentative and conservation approaches, has gained prominence (Zehnder et al., 2007). Coccinellids, being generalist predators, are employed in biological control programmes to manage multiple pests simultaneously (Messelink et al., 2010). Their primary prey is aphids, while secondary food sources include honeydew, pollen, nectar, mites, and coccids (Deligeorgidis et al., 2005). Both the immature stages and adult coccinellids feed on aphids, highlighting their effectiveness as biological control agents. The success of biological control strategies relies on the predator’s consumption rate (Sengonca et al., 2005) and the number of prey attacked at varying densities (Holling, 1959; Solomon, 1949). Therefore, it is imperative to assess the efficacy of natural enemies under laboratory conditions before implementing them in the field. Functional response studies, which examine the predator’s consumption rate at different prey densities, play a significant role in regulating pest populations in agro-ecosystems (Wiedenmann and Smith, 1997). Understanding the dynamics of the prey–predator system is crucial, as it influences the predator’s competence in controlling pests (Holling, 1965; Schenk and Bacher, 2002). Predator–prey interactions serve as a key indicator to evaluate the functional response of a biocontrol agent, reflecting its biocontrol efficacy (Michaud, 2012). Functional response parameters, such as attack rate and handling time, are essential in determining a predator’s ability to keep prey below economic threshold levels (Fathi and Nouri-Ganbalani, 2010). The type of functional response directly affects the effectiveness of the predator, with type I indicating a linear relationship between prey density and the maximum number of prey killed, type II showing a decreasing asymptotic relationship, and type III being positively density-dependent (Bassim, 2003). Ladybird beetles exhibiting type II and type III functional responses are considered effective biocontrol agents (Bayoumy, 2011; Pervez and Omkar, 2005). The type of functional response is influenced by several factors, including predator life stage and sex, which affect foraging behaviour and efficiency. Juvenile predators may have lower foraging efficiency compared to adults due to inexperience, smaller size, and limitations in capturing larger prey (Rashedi et al., 2019). In contrast, adults, particularly females, exhibit higher foraging efficiency, especially during reproduction periods when energy demands are greater (Farhadi et al., 2010). In this study, we evaluated the feeding potential and functional response of Oenopia sauzeti (Mulsant) (Coccinellidae: Coleoptera) fed on different densities of Macrosiphum euphorbiae (Thomas) (Aphididae: Hemiptera) nymphs in the laboratory to assess the potential of coccinellids as biological control agents.

Materials and methods

Feeding potential

The feeding potential of different development stages of O. sauzeti (first instar, second instar, third instar, fourth instar, adult male, and adult female) was studied on different developmental stages of M. euphorbiae. Newly emerged predators of a particular stage were obtained from an egg cohort and released individually onto Petri plates containing tomato leaves with a known number of aphids of a particular stage (10–80 aphids) placed on moist blotting paper. After 24 h, the predator was picked carefully and released into another Petri plate containing the same number of aphids. The procedure was repeated until the predator died. The data on daily prey consumption were recorded after every 24 h until they entered the next stage, and the prey was changed daily. The experiment was replicated ten times. The number of aphids consumed per day by each instar of predator and adult (male and female) was calculated. Data thus obtained were used to calculate the prey consumed during the life stage, entire lifetime, and per day. The data of daily survival and prey consumption of each individual were analyzed using the CONSUME-MS Chart (Chi, 2020), and different prey consumption parameters were calculated using the following variables.

c_xj = mean consumption rate of an individual of age x and stage j

s_xj = probability that a newly laid egg can survive to age x and stage j.

1.Age-specific predation rate (k_x)

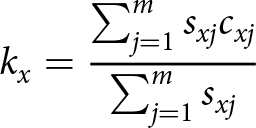\begin{equation*}{k_x} = \frac{{\mathop \sum \nolimits_{j = 1}^m {s_{xj}}{c_{xj}}}}{{\mathop \sum \nolimits_{j = 1}^m {s_{xj}}}}\end{equation*}

2.Age specific net predation rate (q_x)

\begin{equation*}{q_x} = {k_x}{l_x}\end{equation*}

3.Net predation rate (C ₀)

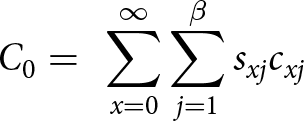\begin{equation*}{\text{ }}{C_0} = {\text{ }}\mathop \sum \limits_{x = 0}^\infty \mathop \sum \limits_{j = 1}^\beta {s_{xj}}{c_{xj}}\end{equation*}

4.Transformation rate (Q_p)

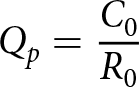\begin{equation*}{Q_p} = \frac{{{C_0}}}{{{R_0}}}\end{equation*}

5.Stable host feeding rate ( $\varphi$)

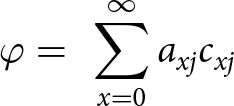\begin{equation*}\varphi = {\text{ }}\mathop \sum \limits_{x = 0}^\infty {a_{xj}}{c_{xj}}\end{equation*}

6.Finite consumption rate (ω)

\begin{equation*}\omega = \lambda \varphi \end{equation*}

Functional response

Functional responses of the O. sauzeti (first instar, second instar, third instar, fourth instar, adult male, and adult female) were studied to different developmental stages at varying densities of the prey aphid at 25 ± 0.5°C, 70 ± 5% relative humidity and 14L:10D photoperiod. The prey densities used were 2, 4, 8, 12, 16, and 22 for first instar; 5, 10, 15, 20, 25, and 30 for second instar; 10, 20, 40, 60, and 80 for third instar, female, and male; and 10, 20, 40, 80, and 100 for fourth instar of the predator. Each prey density was replicated ten times. The prey densities were decided for each stage based on a preliminary experiment carried out to study their feeding over a 24 h period. After allocating the prey at different densities, one predator was confined into each Petri plate. The data on the number of prey eaten by each predator were recorded after 24 h.

Data analysis

The data generated on functional response were analysed using the predation data for 24 h. A logistic regression between the proportion of prey consumed and prey density offered was fitted to determine the shape (e.g. type I or type II) of the functional response:

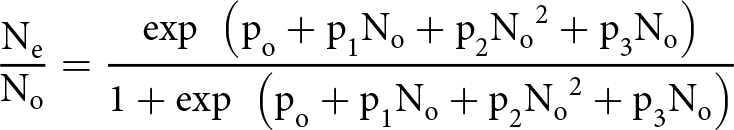\begin{equation*}{{{{\textrm{N}}_{\textrm{e}}}} \over {{{\textrm{N}}_{\textrm{o}}}}} = {{\exp {\textrm{ }}\left( {{{\textrm{p}}_{\textrm{o}}} + {\textrm{p}_1}{{\textrm{N}}_{\textrm{o}}} + {\textrm{p}_2}{{\textrm{N}}_{\textrm{o}}}^2 + {\textrm{p}_3}{{\textrm{N}}_{\textrm{o}}}} \right)} \over {1 + \exp {\textrm{ }}\left( {{{\textrm{p}}_{\textrm{o}}} + {\textrm{p}_1}{{\textrm{N}}_{\textrm{o}}} + {\textrm{p}_2}{{\textrm{N}}_{\textrm{o}}}^2 + {\textrm{p}_3}{{\textrm{N}}_{\textrm{o}}}} \right)}}\end{equation*}

where ${{\textrm{N}}_{\textrm{e}}}{\textrm{}}$ is the number of prey eaten; ${{\text{p}}_{\text{o}}}$is the initial number of preys, ${N_o}$ is the intercept, p₁ is the linear coefficient, p₂ is the quadratic coefficient, and p₃ is the cubic coefficient. A true type I functional response is only possible when handling time is equal to zero, and predators do not reach satiation point, which seems to be an unrealistic situation (Holling, 1959). The sign of the linear coefficient in this model determines the type of functional response: not significant means type I; significantly negative means type II; and if the linear is significantly positive and the quadratic term is significantly negative, a type III response is inferred (Juliano, 2001). Since in each case the type of functional response was a type II, Roger’s random predator equation (for predators) for a type II response was applied to estimate the parameters like handling time (T_h) and attack rate (a) (Rogers et al., 1972).

Roger’s random equation:

\begin{equation*}{N_e} = N\left[ {1 - \exp \left\{ {a\left( {{T_h}{N_e} - aT} \right)} \right\}} \right]\end{equation*}

where N_e is the number of prey eaten per predator, N is the prey density offered, T is the duration of the experiment (24 h), T_h is the handling time, i.e. time required by the predator to pursue, kill, and digest the prey, and a is the predation coefficient or predator’s attack rate. The value a/T_h indicates the effectiveness of the predator, which was calculated by dividing a by T_h, and the maximum theoretical predation rate k = T/T_h was also calculated.

Results

Feeding potential of O. sauzeti against different instars of M. euphorbiae on tomato

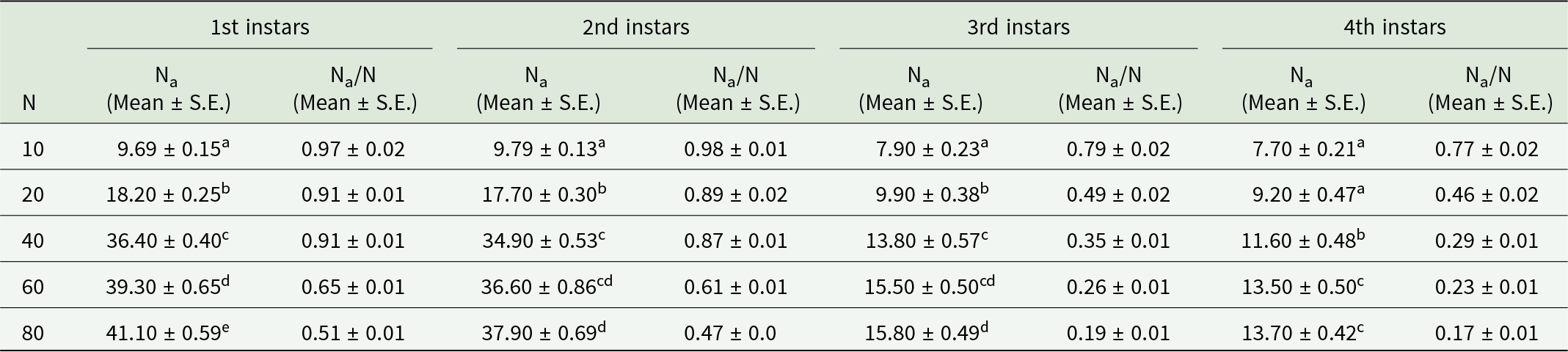
The feeding potential of first, second, third, and fourth instar grubs of O. sauzeti was recorded as 14.73, 53.15, 56.82, and 198.75 aphids, respectively, when reared on first instar of M. euphorbiae. The four larval instars of O. sauzeti consumed an average of 11.87, 46.79, 35.50, and 185.00 aphids when offered second instar of M. euphorbiae, respectively. The total mean consumption of grubs of O. sauzeti was 9.07, 26.93, 25.92, and 107.58 aphids during the first, second, third, and fourth instars, respectively, on the third instar of M. euphorbiae. An average of 5.27, 17.36, 20.33, and 82.67 aphids were eaten by respective instars on the fourth instar of M. euphorbiae (table 1). The female adults of O. sauzeti consumed more number of aphids compared to the male adults.

Table 1. Consumption of O. sauzeti on different instars of M. euphorbiae on tomato

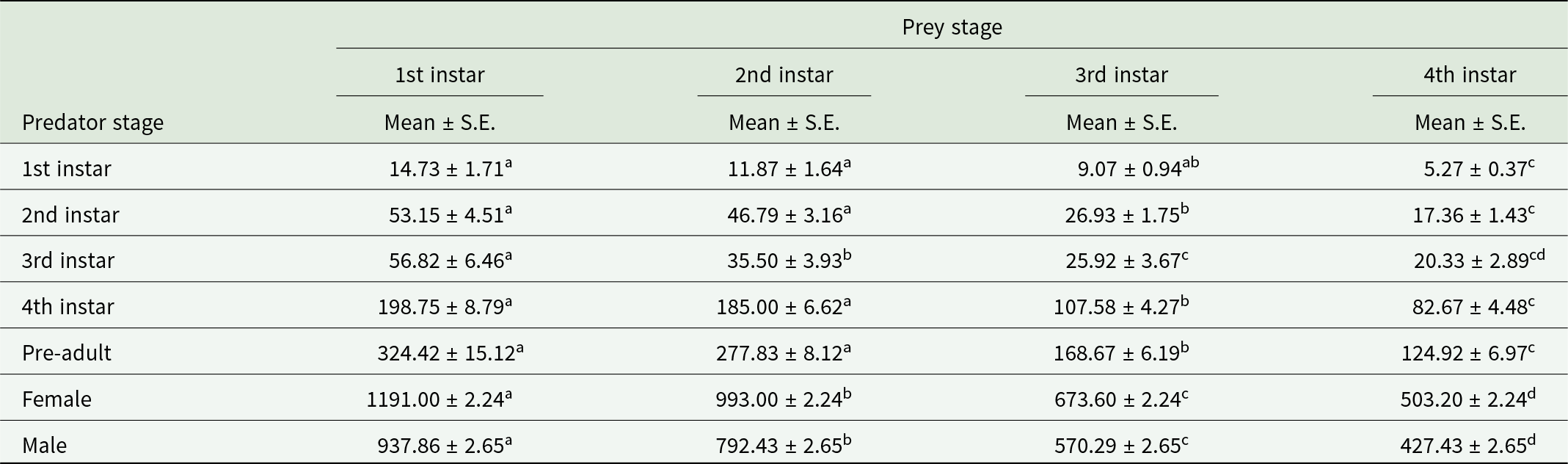
Mean values in a row superscripted with same letter do not differ significantly at p = 0.05.

The single individual of O. sauzeti consumed 1104.53, 936.53, 634.07, and 473.20 aphids in one generation when reared on first, second, third, and fourth instars of M. euphorbiae, respectively. The net consumption rate of predators on the first instar of prey was statistically at par with that on the second instar of prey but different from that on the third and fourth instars of potato aphids. The stable consumption rate was 18.24, 15.28, 9.48, and 7.29 aphids, while the finite consumption rate was 20.84, 17.63, 10.95, and 8.35 aphids on the first, second, third, and fourth instars of M. euphorbiae, respectively. The O. sauzeti consumed 27.34, 21.41, 12.18, or 12.21 aphids of the respective instars to produce an individual (table 2).

Table 2. Consumption parameter of O. sauzeti on different instars of M. euphorbiae on tomato

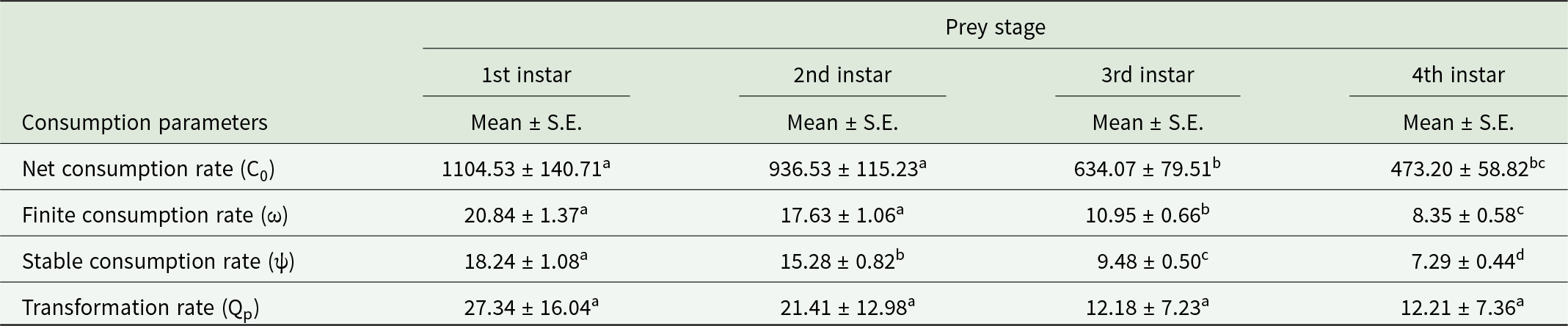
Mean values in a row superscripted with same letter do not differ significantly at p = 0.05.

O. sauzeti, when reared on the varied stages of M. euphorbiae, started to feed at the pivotal age of 2 days with a 100% survival rate. After the 2nd day of the pivotal age, the survival rate of the predator started to decline and finally reached zero at the pivotal ages of the 42nd, 45th, 46th, and 44th days when preyed on the first, second, third, and fourth instars of M. euphorbiae, respectively. O. sauzeti larvae started to feed on the 2nd day after oviposition and consumed an average of 2.20, 1.67, 1.53, and 0.53 first, second, third, and fourth instars, respectively. When fed the on first instar of M. euphorbiae, O. sauzeti consumption increased continuously up to the 10th day (66.33 aphids) and then declined to 14.00 aphids on the 42nd day of pivotal age. The net age-specific feeding rate on 10th day of pivotal age was 53.07 aphids (fig. 1). Likewise, when offered the second instar of M. euphorbiae, O. sauzeti consumption increased continuously up to the 8th day (43.08 aphids) and then declined to 28.00 aphids on the 45th day of pivotal age, and on the highest consumption day, the net age-specific feeding rate was 34.47 aphids (fig. 2). The age-specific prey feeding (k_x) and net age-specific prey feeding (q_x) of O. sauzeti were maximum on the 9th day of pivotal age (k_x = 34.25 and q_x = 27.40) and declined to 11.50 aphids on the 46th day when fed on the third instar of M. euphorbiae (fig. 3). The age-specific prey feeding (k_x) and net age-specific prey feeding (q_x) of O. sauzeti reared on fourth instars of aphids increased to a peak value of 24.83 and 19.87 preys/predator, respectively, on the 10th day and declined to 12.00 aphids on the 44th day (fig. 4).

Figure 1. Predation rate of O. sauzeti on 1st instar of M. euphorbiae on tomato.

Figure 2. Predation rate of O. sauzeti on 2nd instar of M. euphorbiae on tomato.

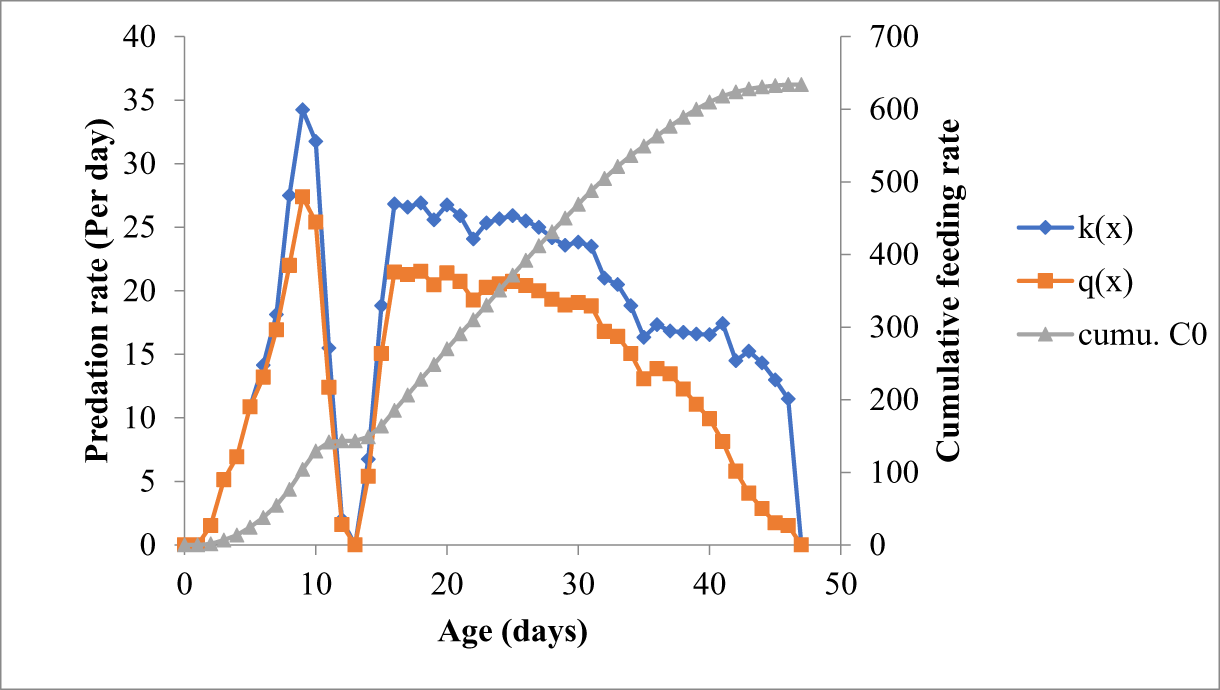
Figure 3. Predation rate of O. sauzeti on 3rd instar of M. euphorbiae on tomato.

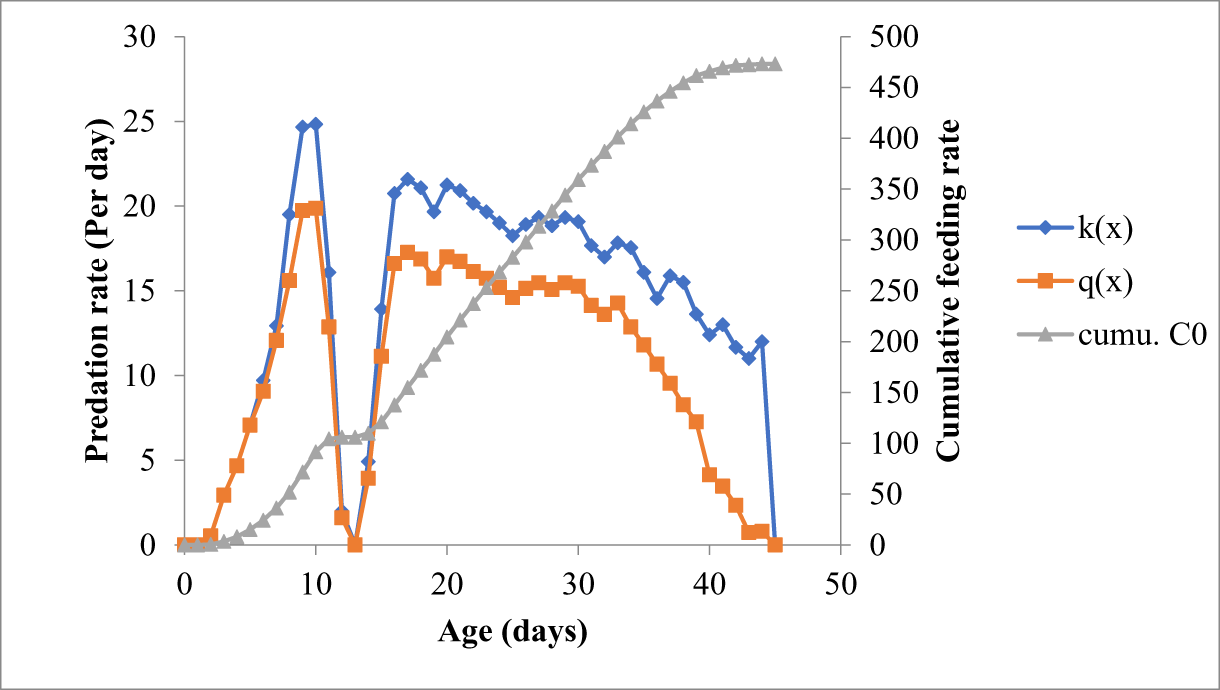
Figure 4. Predation rate of O. sauzeti on 4th instar of M. euphorbiae on tomato.

Functional response of O. sauzeti to different stages of M. euphorbiae on tomato

A type II functional response of O. sauzeti was observed against first, second, third, and fourth instars of aphids of M. euphorbiae, and a significantly negative linear coefficient was obtained after logistic regression analysis for the proportion of prey consumed (N_a/N) as a function of initial prey density (N) (table 3). After confirming the type of functional response, Roger’s random predator equation for a type II functional response was applied to estimate the functional response parameters. The attack rate of the first instars of O. sauzeti was 0.007 h⁻¹, whereas the handling time was 8.580 h on the first instars of potato aphid. The first instars of O. sauzeti were expected to consume 3.437 first instar aphids of M. euphorbiae. The maximum attack rate (0.0.30 h⁻¹) and minimum handling time (1.318 h) for second instars of predators were recorded on first instars of prey. The attack rate of 0.098 h⁻¹ was maximum for third instars of O. sauzeti when feeding on first instars of M. euphorbiae followed by second instars. The handling time of 0.351 h⁻¹ was minimum for third instars of O. sauzeti when offered first instars of M. euphorbiae followed by second instars. The attack rate (a) was maximum (0.098 h) for third instar predators when feeding on first instars of aphids. For fourth instars of predator, the maximum attack rate (0.112 h⁻¹) and minimum handling time (0.264 h) were on first instars of prey followed by second instars, which is statistically similar (table 4). The maximum attack rate for females and males of O. sauzeti was recorded on first instars of potato aphid. The attack rates estimated for female and male of O. sauzeti were 0.111 h⁻¹ and 0.106 h⁻¹ on first instars of prey, respectively. The minimum handling time for female (0.269 h) and male (0.264 h) of predators was recorded on the second and first instars of prey.

Table 3. Linear coefficients of logistic regression between proportion of prey eaten (N_a/N) and initial prey density (N) of O. sauzeti to different stages of M. euphorbiae on tomato

Table 4. Functional response parameters of O. sauzeti against different instars of M. euphorbiae on tomato

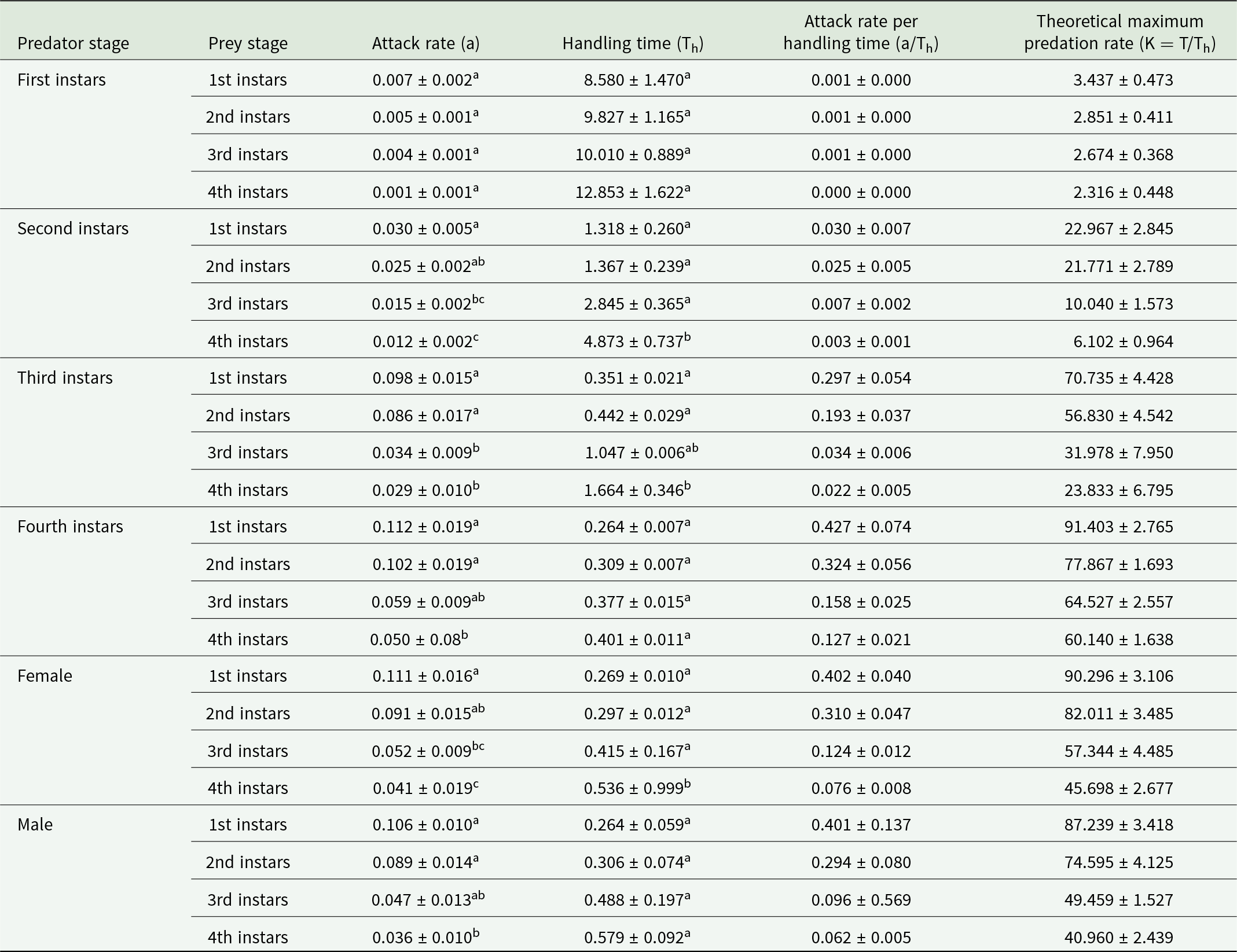
Mean values in a column (for a particular predator stage) superscripted with same letter do not differ significantly at p = 0.05.

First instars

The first instars of O. sauzeti were offered with prey densities of 2, 4, 8, 12, 16, and 22 first, second, third, and fourth instars nymphs of potato aphids, consumed an average of 0.70, 1.20, 1.70, 2.10, 2.30, and 2.40; 0.60, 0.90, 1.40, 1.90, 2.20, and 2.30; 0.41, 0.60, 1.00, 1.20, 1.30, and 1.30; and 0.41, 0.60, 0.90, 1.00, 1.10, and 1.10 aphids/predator, respectively. The maximum number of aphids consumed at the highest prey density (table 5, fig. 5). The number of prey consumed increased significantly with the increase in the prey density offered until reaching the upper asymptote.

Figure 5. Functional response of O. sauzeti 1st instars against different instars of M. euphorbiae on tomato.

Table 5. Functional response of first instars of O. sauzeti against different instars of M. euphorbiae on tomato

Mean values in a column superscripted with same letter do not differ significantly at p = 0.05. N, prey density offered; N_a, prey consumed.

Second instars

Likewise, prey densities of 5, 10, 15, 20, 25 and 30 were offered to second instars of O. sauzeti, consumed an average of 3.60, 6.60, 9.10, 13.70, 14.40, and 14.50; 3.40, 5.50, 7.90, 11.50, 12.30, and 12.10; 2.20, 3.20, 4.40, 6.30, 6.50, and 6.30; and 1.60, 2.40, 3.70, 4.50, 5.00, and 5.10 first, second, third, and fourth instars of aphids, respectively. Prey consumption increased as the prey density increased until the maximum equilibrium point, beyond which it slightly reduced or levelled off (table 6, fig. 6).

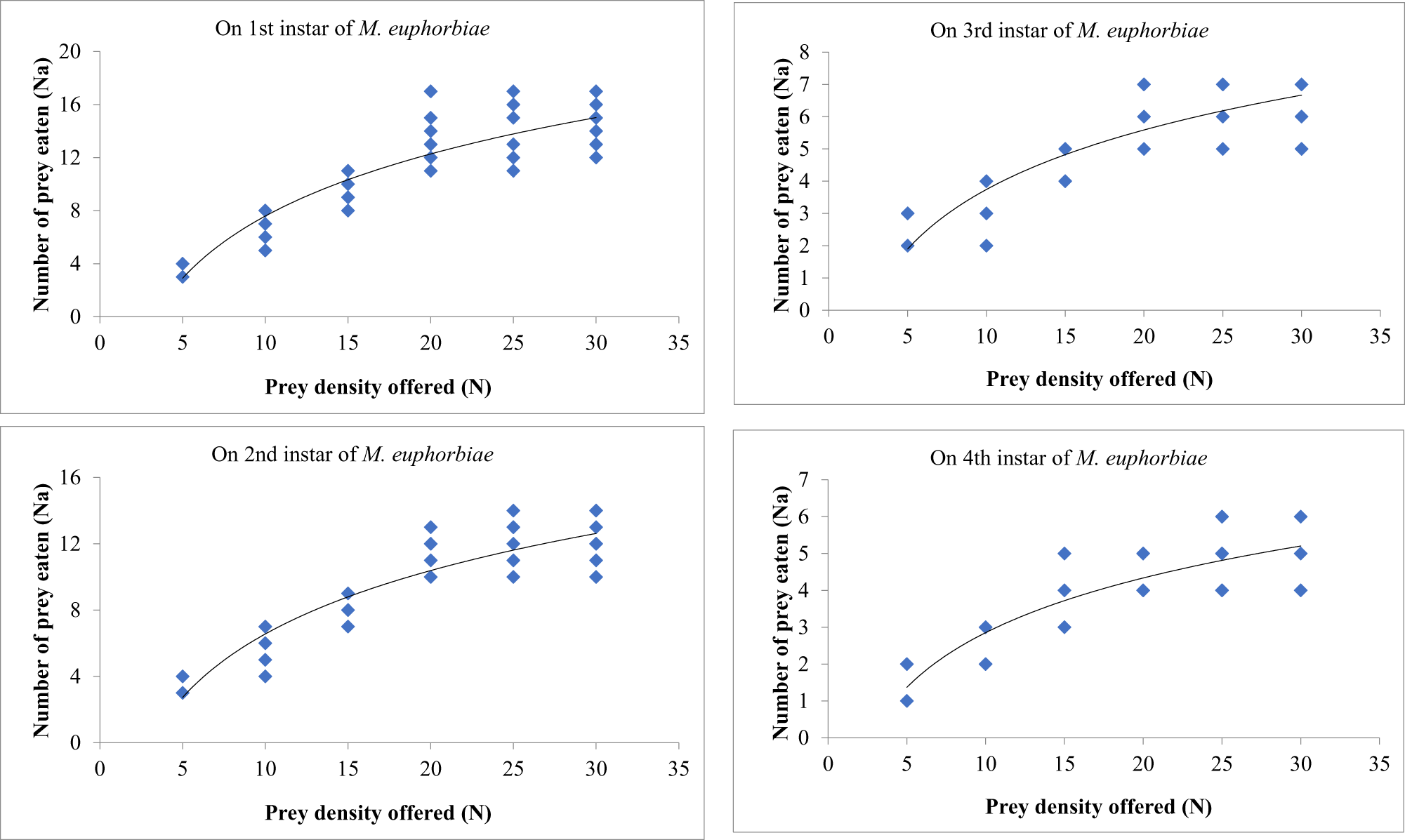
Figure 6. Functional response of O. sauzeti 2nd instars against different instars of M. euphorbiae on tomato.

Table 6. Functional response of second instars of O. sauzeti against different instars of M. euphorbiae on tomato

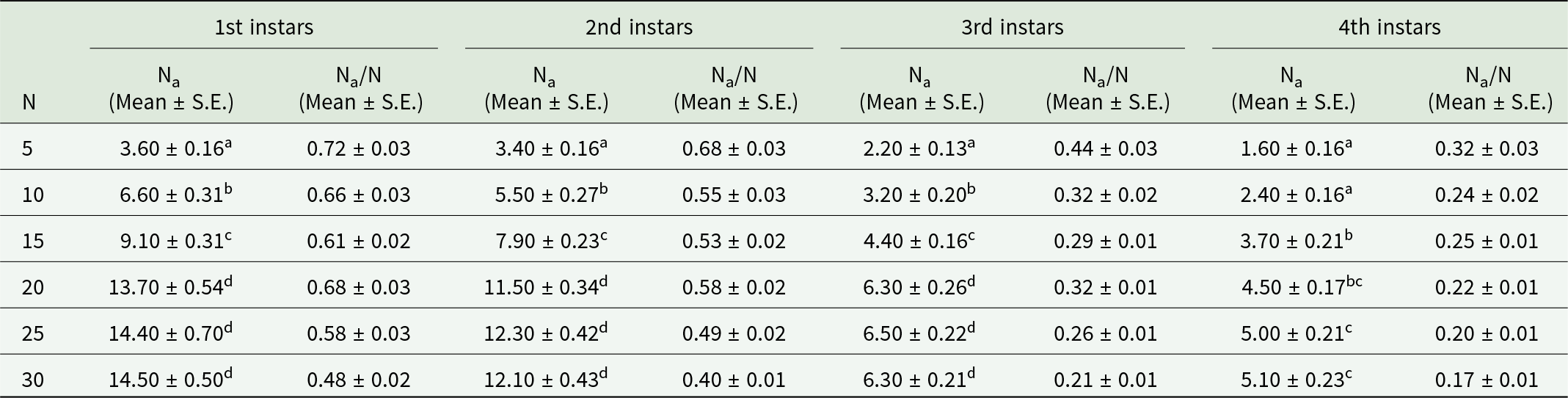
Mean values in a column superscripted with same letter do not differ significantly at p = 0.05. N, prey density offered; N_a, prey consumed.

Third instars

The prey densities of 10, 20, 40, 60, and 80 were offered to third instars of O. sauzeti, consumed an average of 9.19, 17.20, 29.40, 31.60, and 32.10; 9.29, 17.10, 26.20, 29.40, and 29.70; 7.40, 9.70, 11.30, 13.40, and 13.70; and 7.10, 9.40, 10.30, 11.20, and 11.40 first, second, third, and fourth instars potato aphids, respectively (table 7, fig. 7). In all cases, the proportion of prey consumed is maximum at the lowest prey density and minimum at the highest prey density.

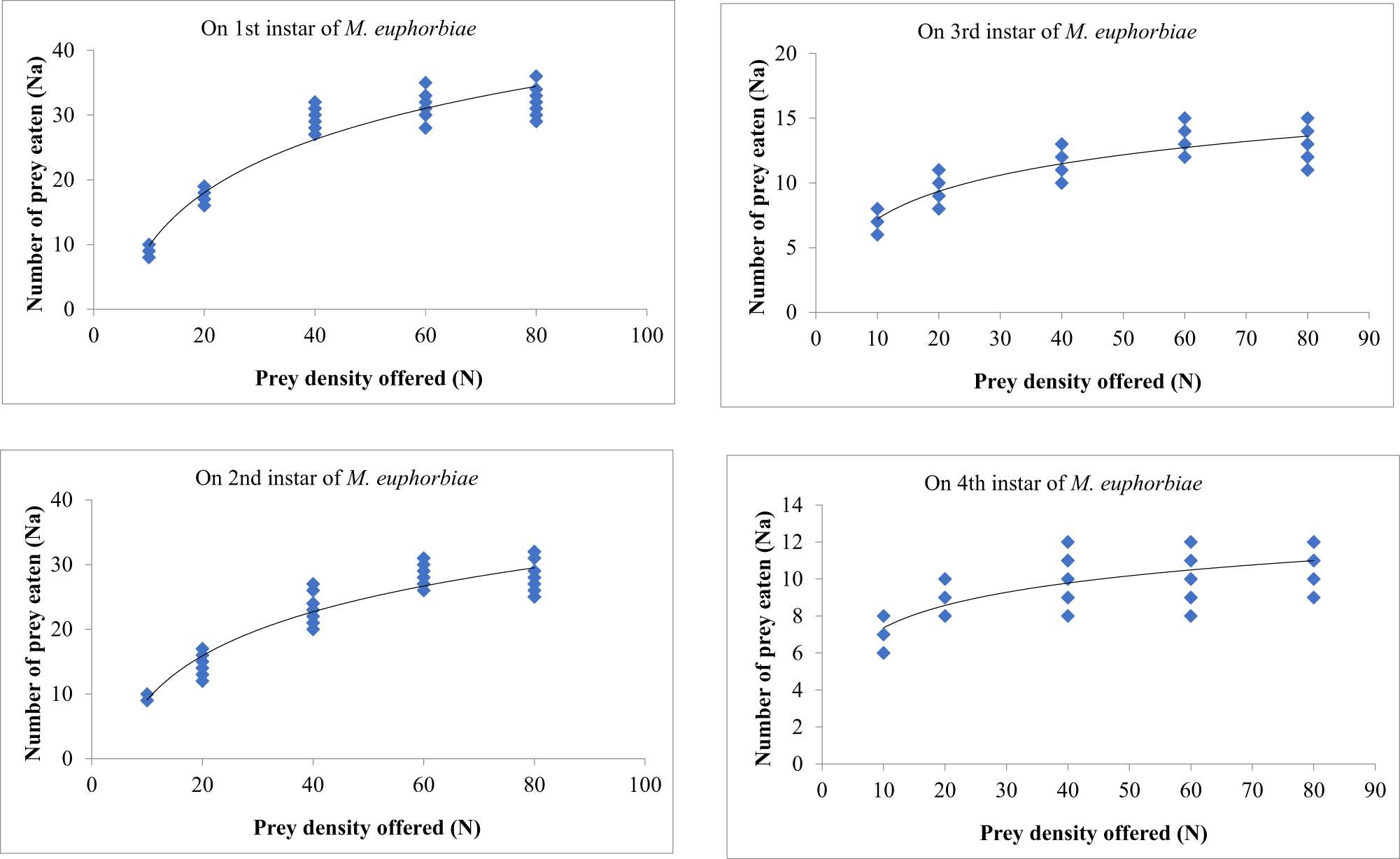
Figure 7. Functional response of O. sauzeti 3rd instars against different instars of M. euphorbiae on tomato.

Table 7. Functional response of third instars of O. sauzeti against different instars of M. euphorbiae on tomato

Mean values in a column superscripted with same letter do not differ significantly at p = 0.05. N, prey density offered; N_a, prey consumed.

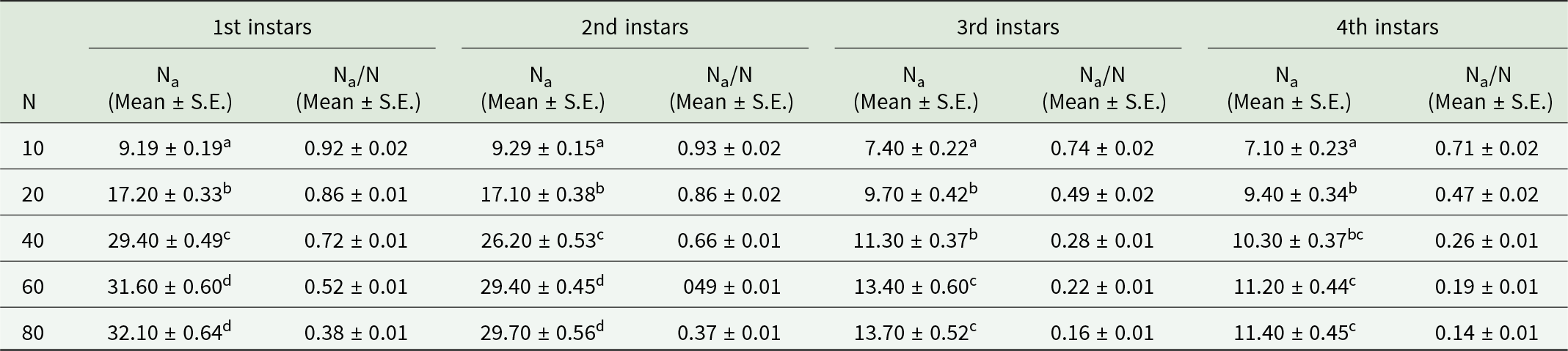
Fourth instars

The fourth instars of O. sauzeti were offered prey densities of 10, 20, 40, 80, and 100 first, second, third, and fourth instars, consumed an average of 9.89, 19.29, 38.10, 49.60, and 51.30; 9.69, 19.29, 35.30, 42.90, and 43.40; 8.78, 15.40, 25.10, 30.90, and 31.20; and 8.60, 14.60, 24.60, 28.60, and 28.80 aphids/predator, respectively. The maximum number of aphids consumed at the highest prey density (table 8, fig. 8). With an increase in prey density (N), the number of prey consumed by the predator increased, and the proportion of prey consumed decreased in all cases.

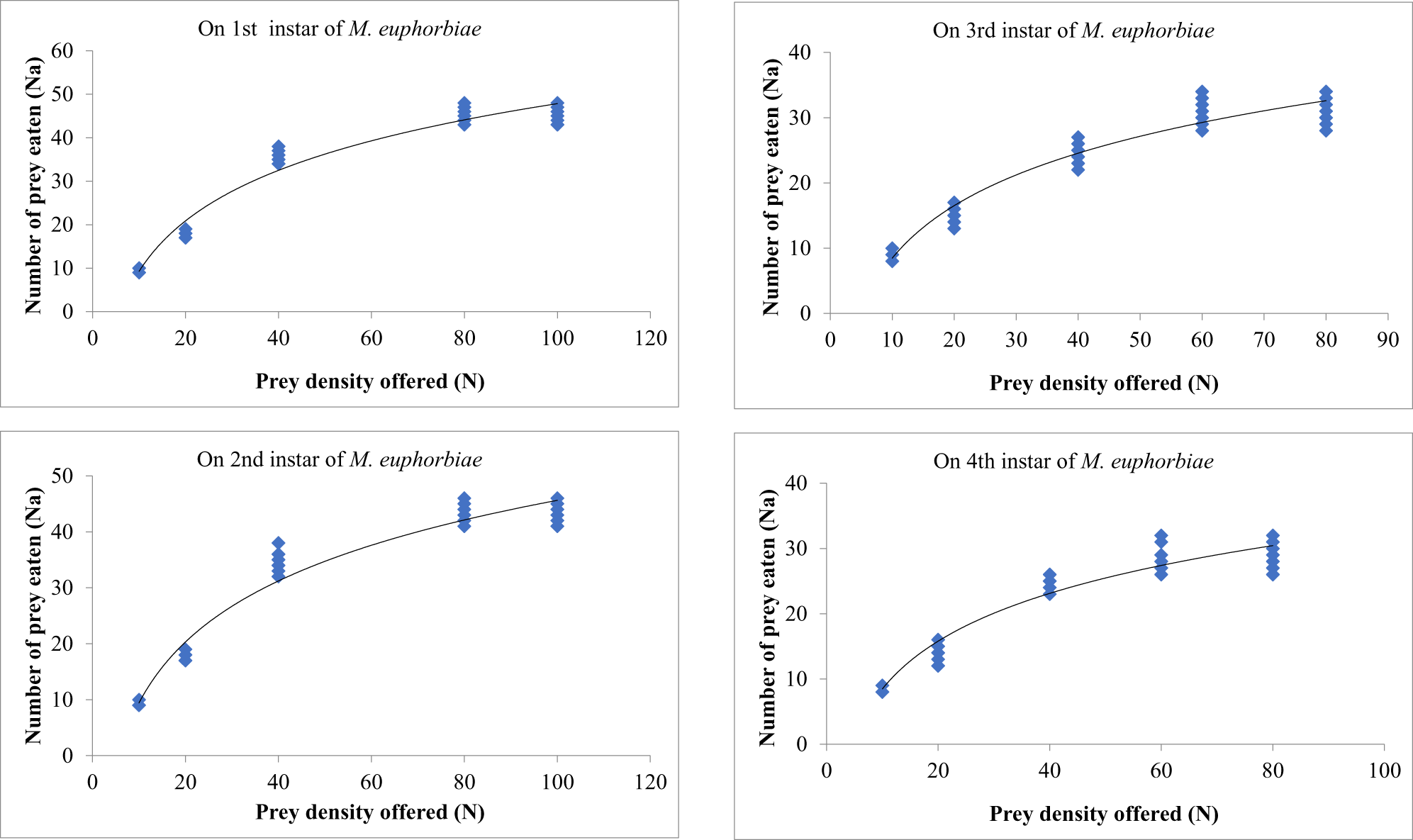
Figure 8. Functional response of O. sauzeti 4th instars against different instars of M. euphorbiae on tomato.

Table 8. Functional response of fourth instars of O. sauzeti against different instars of M. euphorbiae on tomato

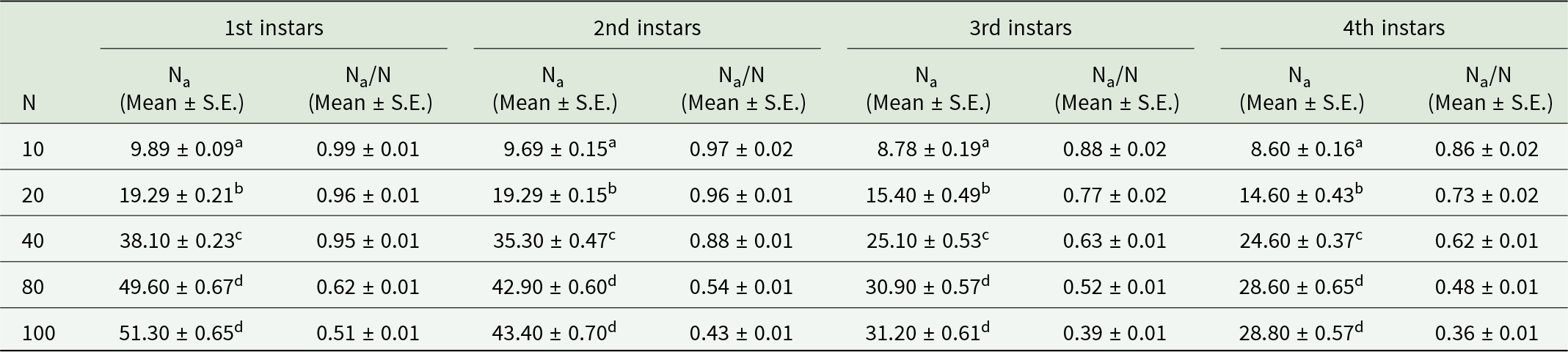
Mean values in a column superscripted with same letter do not differ significantly at p = 0.05. N, prey density offered; N_a, prey consumed.

Female

The prey densities of 10, 20, 40, 60 and 80 were offered to female O. sauzeti, consumed an average of 9.79, 18.70, 36.10, 39.90, and 41.30; 9.59, 17.90, 34.50, 38.50, and 39.60; 8.30, 9.70, 14.80, 16.50, and 16.80; and 7.90, 8.80, 12.90, 14.50, and 14.80 first, second, third, and fourth instars potato aphids, respectively (table 9, fig. 9). The prey consumption increased with the increase in the prey density, and the fraction of the prey eaten decreased with the increasing prey density.

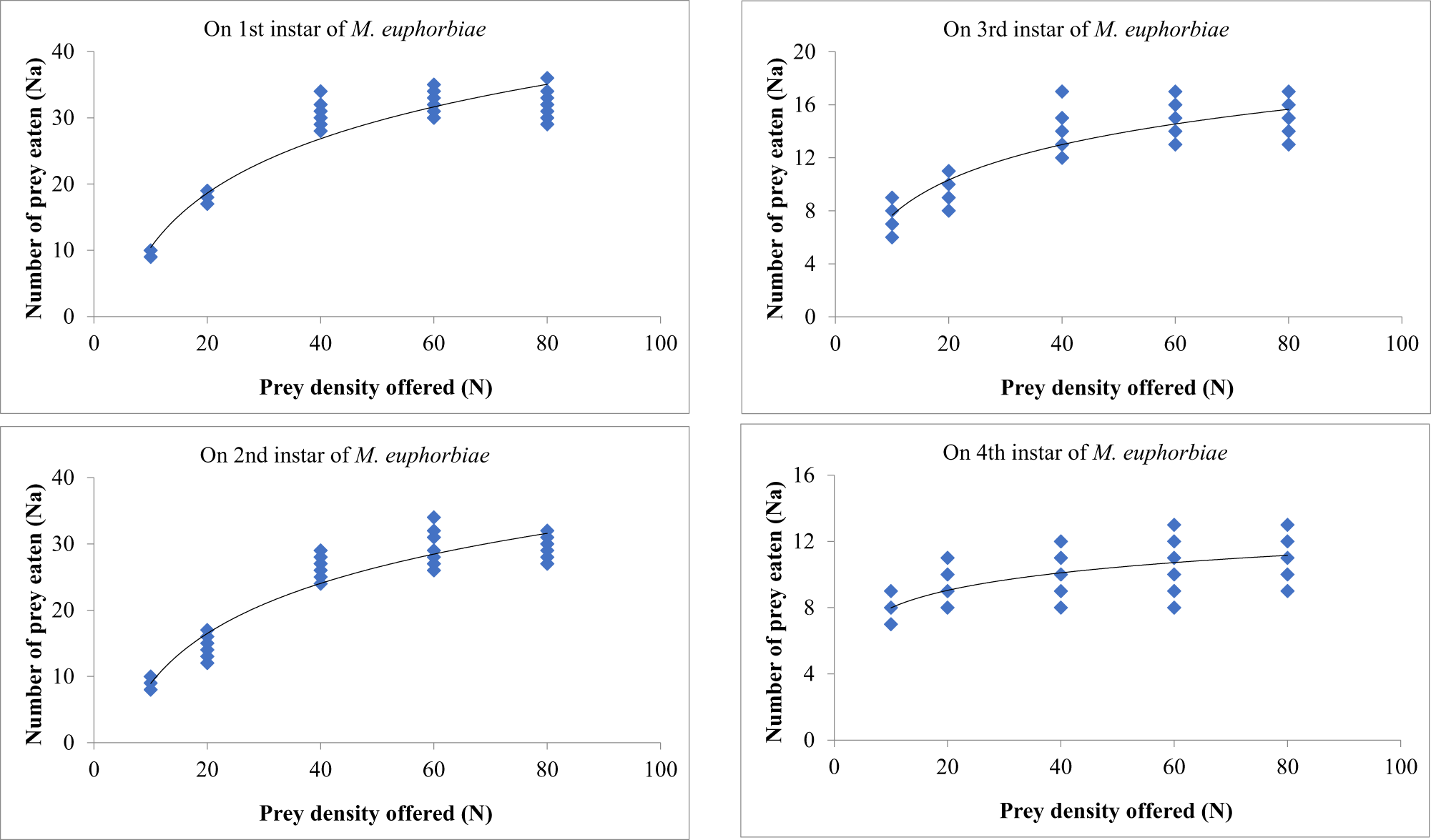
Figure 9. Functional response of O. sauzeti female against different instars of M. euphorbiae on tomato.

Table 9. Functional response of female of O. sauzeti against different instars of M. euphorbiae on tomato

Mean values in a column superscripted with same letter do not differ significantly at p = 0.05. N, prey density offered; N_a, prey consumed.

Male

Similarly, O. sauzeti males were offered prey densities of 10, 20, 40, 60 and 80 first, second, third and fourth instars of M. euphorbiae offered, consumed an average of 9.69, 18.20, 36.40, 39.30, and 41.10; 9.79, 17.70, 34.90, 36.60, and 37.90; 7.90, 9.90, 13.80, 15.50, and 15.80; and 7.70, 9.20, 11.60, 13.50, and 13.70 aphids/predator, respectively. The maximum number of aphids consumed at the highest prey density (table 10, fig. 10). Prey consumption increased as the prey density increased until the maximum equilibrium point, beyond which it slightly reduced.

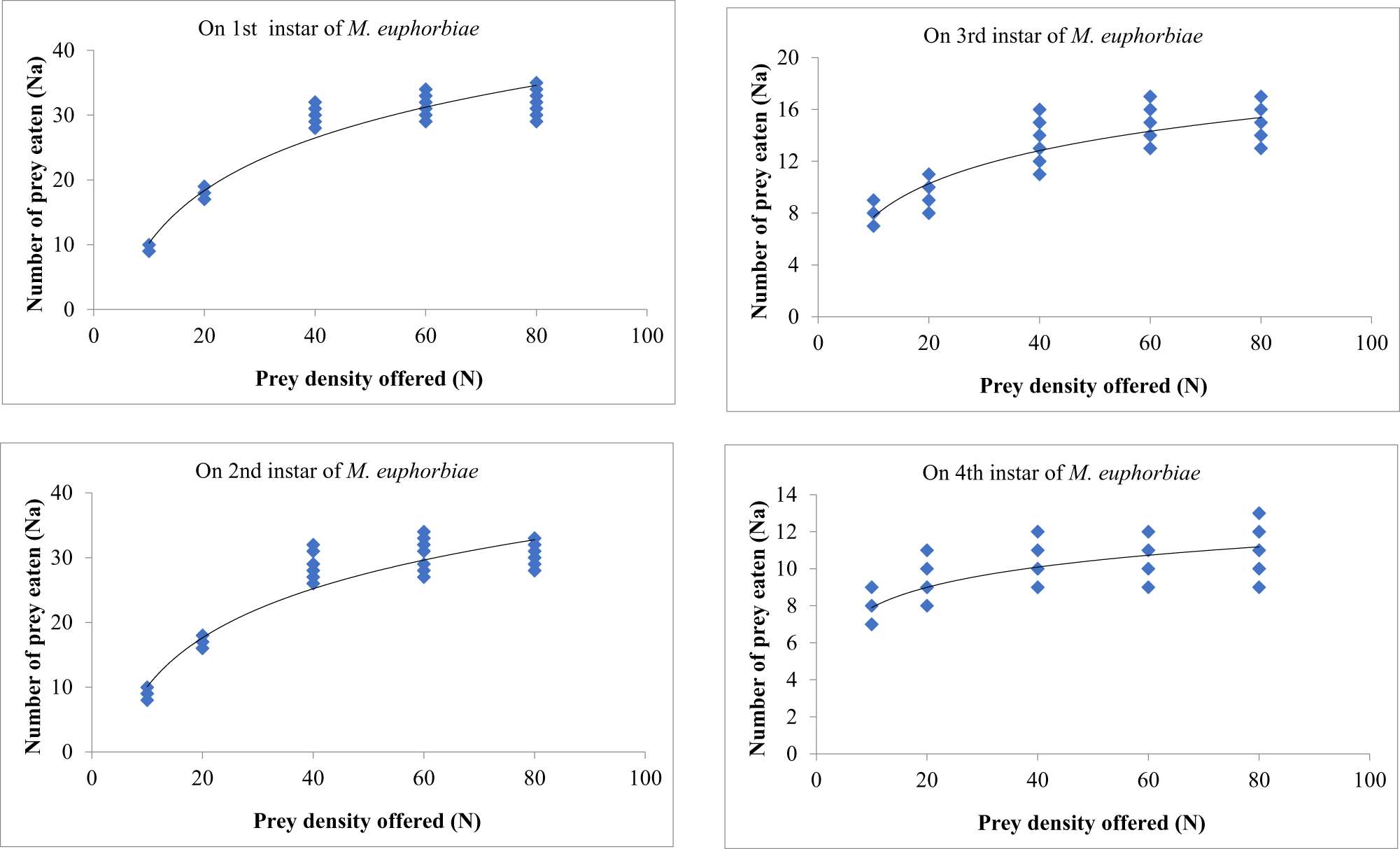
Figure 10. Functional response of O. sauzeti male against different instars of M. euphorbiae on tomato.

Table 10. Functional response of male of O. sauzeti against different instars of M. euphorbiae on tomato

Mean values in a column superscripted with same letter do not differ significantly at p = 0.05. N, prey density offered; N_a, prey consumed.

Discussion

The ladybird beetles, O. sauzeti, are acknowledged as potential biological control agents against aphids, emphasizing their economic importance (Iftikhar et al., 2018). Our study aims to contribute insights into the feeding potential and consumption parameters of O. sauzeti across different instars of M. euphorbiae in tomato crops. Results revealed significant variations in the feeding potential of O. sauzeti immature stages. The fourth instar exhibited the highest feeding potential, followed by the third instar, while the first instar displayed the lowest feeding potential on all prey stages. In parallel, Unal et al. (2017) noted a similar trend in Coccinella septempunctata Linnaeus, with increasing predatory potential up to the fourth instar, which was the most voracious consumer of M. rosae. The similar trend was found in the present study, where the predatory potential of grubs against M. euphorbiae increased with an increase in age of predators and fourth instar consumed highest aphids. Consistent with prior studies, our findings align with Rashed et al. (2020), reporting increased predatory potential in C. undecimpunctata larval instars against Schizaphis graminum (Rondani) and Aphis craccivora (Koch) aphids. C. undecimpunctata first, second, third, and fourth larval instars consumed 17.36, 28.21, 37.93, and 86.64 S. graminum aphids and 15.15, 22.15, 34.64, and 90.38 A. craccivora aphids, respectively. The predatory potential of different instars of C. septempunctata and O. kirbyi was 579.92 and 535.90 against A. gossypii (Deeksha, 2018). Discrepancies were observed in comparison with the results of Gaikwad et al. (2021) who reported the lifetime consumption rate of adult females of O. kirbyi was 560.16 aphids and adult males consumed 491 aphids. The slight variation is probably due to the size of the prey and the predators used in the experiment. The net predation rate (C₀) for O. sauzeti in our study concurs with the findings of Farhadi et al. (2011), recording a net predation rate of 1127.10 aphids. Adult O. sauzeti consumed an average of 1043.33 first instar aphids and 876.00 second instar aphids throughout their entire life cycle. The results slightly aligned with the finding of Vasista et al. (2021), who recorded that Cheilomenes sexmaculata Fabricius consumed an average of 1167.20 and 949.80 aphids, whereas C. transversalis consumed 950.6 and 843.60 A. craccivora and A. gossypii aphids, respectively, in its entire life cycle.

O. sauzeti exhibited a type II functional response against the M. euphorbiae in the present study. This type II functional response, common in coccinellids, suggests negative density-dependent mortality. A natural enemy with a type II functional response is considered a negative density-dependent mortality factor and hence a poor regulator of the pest population (Hassell, 2000). The present results are in line with the findings of Khan and Mir (2008), who estimated the functional response of four coccinellids, viz. Adalia tetraspilota (Hope), C. septempunctata, Calvia punctata (Mulsant), and Hippodamia variegata (Goeze) to varying densities of A. pomi and observed a convex (type II) functional response in all the species to their target pests. A type II functional response was also reported for H. variegata to A. gossypii (Dekhordi et al., 2012), C. septempunctata to Lipaphis erysimi (Kalt.) (Gupta et al., 2012), C. septempunctata, H. variegata to A. craccivora (Bayoumy and Awadalla, 2018), H. variegata to M. euphorbiae (Khattawi et al., 2020), and O. kirbyi to M. rosae (Gaikwad et al., 2021). The declining proportion of prey consumption with increasing prey density, indicative of a type II curve, is consistent with various studies. The discussion on type III functional response emphasizes its effectiveness at low pest densities, signifying a learning phase in the natural enemy, whereas type II responses, as observed in O. sauzeti, demonstrate immediate and effective feeding at lower prey densities. The functional response studies tell about the behaviour of natural enemies against changing prey densities. Similarly, Bayoumy and Awadalla (2018) evaluated the H. variegata and C. septempunctata behavioural responses to the changes in the density of M. persicae and A. craccivora. The increase in attack rates and decrease in handling times with predator developmental stages, as observed in our study, correlate with established patterns in the literature. The highest attack rate and lowest handling time by the late instars could be due to the larger body size and ability to move faster than the initial stages. The highest attack rate and lowest handling time were recorded by the fourth instar of the predator on the first instar of prey, which is statistically at par with the second instar of prey. The attack rate of 0.0469 h⁻¹ and handling time of 0.0152 h for all O. conglobata against common pistachio psylla recorded by Hasani, Mehrnejad and Ostovan (2004) were not in accordance with our study due to differences in the prey. The searching efficiency, handling time, and estimated maximum prey consumption of H. variegata on A. fabae were 0.00078, 0.1774, and 135.29, respectively (Jafari and Goldasteh, 2009). The searching efficiency and handling times of the H. variegata females were 0.003 h⁻¹, 0.106 h, 0.122 h⁻¹, and 0.105 h, respectively, against A. gossypii (Dekhordi et al., 2012). This study results are partially in accordance with the results of Gaikwad et al. (2021) who reported the highest attack rate of 0.085 h⁻¹ and the lowest handling time of 0.704 h for O. kirbyi against M. rosae. The predator and prey were almost similar in size, and the prey was very active. The higher T_h recorded compared to our study because the predator struggled too much to handle the prey.

Conclusion

The feeding and functional response parameters highlight the effectiveness of both immature stages and adults of O. sauzeti as efficient biological control agents against M. euphorbiae. As the predator exhibits a type II functional response, this could be more suitable for augmentative biological control in the Integrated Pest Management Programme against the potato aphid, M. euphorbiae. Opting for augmentative biological control with O. sauzeti could serve as a favourable alternative to chemical interventions in managing potato aphids. This approach emphasizes the integration of natural predators into pest management strategies, contributing to sustainable and environmentally friendly practices. However, before making any final recommendations, it is crucial to evaluate the performance of O. sauzeti under actual field conditions. Field assessments will provide a more comprehensive understanding of the predator’s effectiveness in controlling M. euphorbiae in real-world agricultural settings. Manipulating O. sauzeti populations could potentially yield optimal outcomes in the biological control of potato aphids, emphasizing the importance of field-based evaluations in decision-making processes related to pest management strategies.