Hostname: page-component-857557d7f7-zv5th Total loading time: 0 Render date: 2025-12-10T04:54:53.681Z Has data issue: false hasContentIssue false
  • English
  • Français

NOTES ON GENERALISED INTEGRAL POLYNOMIAL PELL EQUATIONS

Part of: Diophantine equations Polynomials and matrices Algebraic number theory: global fields

Published online by Cambridge University Press:  09 December 2025

NGUYEN XUAN THO Open the ORCID record for NGUYEN XUAN THO [Opens in a new window]
NGUYEN XUAN THO*
Affiliation:
Faculty of Mathematics and Informatics, Hanoi University of Science and Technology, 1 Dai Co Viet, Hai Ba Trung, Hanoi, Vietnam
*
e-mail: tho.nguyenxuan1@hust.edu.vn
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a nonzero integer n, Gupta and Saha [‘Integer solutions of the generalised polynomial Pell equations and their finiteness: the quadratic case’, Canad. Math. Bull., to appear] classified all polynomials $x^2+ax+b\in {\mathbb {Z}}[x]$ for which the polynomial Pell equation $P^2-(x^2+ax+b)Q^2=n$ has solutions ${P,Q\in {\mathbb {Z}}[x]}$ with $Q\neq 0$. We generalise their work to the equation $P^2-(f^2+af+b)Q^2=nR$, where f is a fixed polynomial in 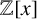${\mathbb {Z}}[x]$. As an application of our results, we study the equation $P^2-D(f)Q^2=n$, where D is a monic, quartic and non square-free polynomial in 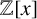${\mathbb {Z}}[x]$. This extends Theorem 1.4 of Scherr and Thompson [‘Quartic integral polynomial Pell equations’, J. Number Theory 259 (2024), 38–56].

Keywords

Pell equationpolynomial Pell equationDiophantine equation

MSC classification

Primary: 11D09: Quadratic and bilinear equations
Secondary: 11C08: Polynomials 11R09: Polynomials (irreducibility, etc.)

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 13
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work was supported by the Vietnam National Foundation for Science and Technology Development (NAFOSTED), grant number 101.04-2023.21.

References

Abel, N. H., ‘Über die Integration der Differential-Formel $\rho dx/\sqrt{R}$ , wenn $R$ und $\rho$ ganze Funktionen sind’, J. reine angew. Math. 1 (1826), 185–221.Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The MAGMA algebra system. I. The user language’, J. Symbolic Comput. 24(3–4) (1997), 235–265.CrossRefGoogle Scholar
Dubickas, A. and Steuding, J., ‘The polynomial Pell equation’, Elem. Math. 59(4) (2004), 133–143.CrossRefGoogle Scholar
Gaunet, M. L., ‘Formes cubiques polynomiales’, C. R. Math. Acad. Sci. Paris 311 (1990), 491–494.Google Scholar
Gupta, A. and Saha, E., ‘Integer solutions of the generalised polynomial Pell equations and their finiteness: the quadratic case’, Canad. Math. Bull., to appear. Published online (27 August 2025).CrossRefGoogle Scholar
Hazama, F., ‘Pell equations for polynomials’, Indag. Math. (N.S.) 8 (1997), 387–397.10.1016/S0019-3577(97)81817-4CrossRefGoogle Scholar
Jedrzejak, T., ‘Polynomial Pell equations and associated hyperelliptic curves’, J. Ramanujan Math. Soc. 34(2) (2019), 263–269.Google Scholar
McLaughlin, J., ‘Polynomial solutions of Pell’s equation and fundamental units in real quadratic fields’, J. London Math. Soc. (2) 67(1) (2003), 16–28.CrossRefGoogle Scholar
Mollin, R. A., ‘Polynomial solutions for Pell’s equation revisited’, Indian J. Pure Appl. Math. 28 (1997), 429–438.Google Scholar
Murru, N., ‘A note on the use of Rédei polynomials for solving the polynomial Pell equation and its generalization to higher degrees’, Ramanujan J. 53(3) (2020), 693–703.10.1007/s11139-019-00233-1CrossRefGoogle Scholar
Nathanson, M. B., ‘Polynomial Pell’s equations’, Proc. Amer. Math. Soc. 56 (1976), 89–92.Google Scholar
Scherr, Z. and Thompson, K., ‘Quartic integral polynomial Pell equations’, J. Number Theory 259 (2024), 38–56.10.1016/j.jnt.2023.12.009CrossRefGoogle Scholar
Schinzel, A., ‘On some problems of the arithmetical theory of continued fractions’, Acta Arith. 6 (1961), 393–413.CrossRefGoogle Scholar
Schinzel, A., ‘On some problems of the arithmetical theory of continued fractions II’, Acta Arith. 7 (1962), 187–298. Corrigendum, ibid. 47 (1986), 295.CrossRefGoogle Scholar
Webb, W. A. and Yokota, H., ‘Polynomial Pell’s equation’, Proc. Amer. Math. Soc. 131(4) (2003), 993–1006.CrossRefGoogle Scholar
Webb, W. A. and Yokota, H., ‘Polynomial Pell’s equation. II’, J. Number Theory 106(1) (2004), 128–141.CrossRefGoogle Scholar
Yokota, H., ‘Solutions of polynomial Pell’s equation’, J. Number Theory 130(9) (2010), 2003–2010.10.1016/j.jnt.2009.12.006CrossRefGoogle Scholar