Hostname: page-component-5b777bbd6c-cp4x8 Total loading time: 0 Render date: 2025-06-19T08:09:39.974Z Has data issue: false hasContentIssue false
  • English
  • Français

SQUARE-FULL VALUES OF QUADRATIC POLYNOMIALS

Part of: Diophantine equations Multiplicative number theory

Published online by Cambridge University Press:  16 May 2025

WATCHARAKIETE WONGCHAROENBHORN Open the ORCID record for WATCHARAKIETE WONGCHAROENBHORN [Opens in a new window]  and
YOTSANAN MEEMARK Open the ORCID record for YOTSANAN MEEMARK [Opens in a new window]
WATCHARAKIETE WONGCHAROENBHORN
Affiliation:
Department of Mathematics and Computer Science, Faculty of Science, Chulalongkorn University, Bangkok 10330, Thailand e-mail: w.wongcharoenbhorn@gmail.com
YOTSANAN MEEMARK*
Affiliation:
Department of Mathematics and Computer Science, Faculty of Science, Chulalongkorn University, Bangkok 10330, Thailand
*
e-mail: yotsanan.m@chula.ac.th
Get access Rights & Permissions [Opens in a new window]

Abstract

A square-full number is a positive integer for which all prime divisors divide the number at least twice. For a relatively prime pair $(a,b)\in \mathbb N\times \mathbb N\cup \{0\}$ and an affine polynomial $f(x)=ax+b$, the number of $n\leqslant N$ such that $f(n)$ is square-full is of order $N^{{1}/{2}}$. For 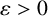$\varepsilon>0$ and an admissible quadratic polynomial $f(x)\in \mathbb Z[x]$, we show that the number of $n\leqslant N$ such that 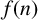$f(n)$ is square-full is at most $O_{\varepsilon ,f}(N^{\varpi +\varepsilon })$ for some absolute constant $\varpi <1/2$. Under the $abc$ conjecture, we expect the upper bound to be $O_{\varepsilon ,f}(N^\varepsilon )$.

Keywords

square-full integersquadratic polynomials

MSC classification

Primary: 11N32: Primes represented by polynomials; other multiplicative structure of polynomial values
Secondary: 11D45: Counting solutions of Diophantine equations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 15
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bateman, P. T. and Grosswald, E., ‘On a theorem of Erdős and Szekeres’, Illinois J. Math. 2 (1958), 88–98.CrossRefGoogle Scholar
Bhargava, M., Shankar, A., Taniguchi, T., Thorne, F., Tsimerman, J. and Zhao, Y., ‘Bounds on 2-torsion in class groups of number fields and integral points on elliptic curves’, J. Amer. Math. Soc. 33 (2020), 1087–1099.CrossRefGoogle Scholar
Bombieri, E. and Schmidt, W. M., ‘On Thue’s equation’, Invent. Math. 88 (1987), 69–81.CrossRefGoogle Scholar
Browning, T., ‘Power-free values of polynomials’, Arch. Math. 96 (2011), 139–150.CrossRefGoogle Scholar
Browning, T. and Shparlinski, I., ‘Square-free values of random polynomials’, J. Number Theory 261 (2024), 220–240.CrossRefGoogle Scholar
Chan, T. H., ‘Squarefull numbers in arithmetic progression II’, J. Number Theory 152 (2015), 90–104.CrossRefGoogle Scholar
Ellenberg, J. and Venkatesh, A., ‘Reflection principles and bounds for class group torsion’, Int. Math. Res. Not. IMRN 2007 (2007), Article no. rnm002.CrossRefGoogle Scholar
Erdős, P. and Szekeres, G., ‘Über die Anzahl der Abelschen Gruppen gegebener Ordnung und über ein verwandtes zahlentheoretisches Problem’, Acta Sci. Math. (Szeged) 7 (1935), 95–102 (in German).Google Scholar
Estermann, T., ‘Einige Sätze über quadratfreie Zahlen’, Math. Ann. 105 (1931), 653–662 (in German).CrossRefGoogle Scholar
Granville, A., ‘ABC allows us to count squarefrees’, Int. Math. Res. Not. IMRN 1998 (1998), 991–1009.CrossRefGoogle Scholar
Heath-Brown, D. R., ‘Counting rational points on algebraic varieties’, in: Analytic Number Theory, Lecture Notes in Mathematics, 1891 (eds. Perelli, A. and Viola, C.) (Springer, Berlin–Heidelberg, 2006).Google Scholar
Heath-Brown, D. R., ‘Sums and differences of three $k$ -th powers’, J. Number Theory 129 (2009), 1579–1594.CrossRefGoogle Scholar
Heath-Brown, D. R., ‘Square-free values of ${n}^2+1$ ’, Acta Arith. 155 (2012), 1–13.CrossRefGoogle Scholar
Helfgott, H. A. and Venkatesh, A., ‘Integral points on elliptic curves and 3-torsion in class groups’, J. Amer. Math. Soc. 19 (2006), 527–550.CrossRefGoogle Scholar
Reuss, T., ‘Pairs of $k$ -free numbers, consecutive square-full numbers’, Preprint, 2014, arXiv:1212.3150.Google Scholar