Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T10:10:44.909Z Has data issue: false hasContentIssue false
  • English
  • Français

Actions of Finite Groups on Rn+k with Fixed Set Rk

Published online by Cambridge University Press:  20 November 2018

Ian Hambleton  and
Ib Madsen
Ian Hambleton
Affiliation:
McMaster University, Hamilton, Ontario
Ib Madsen
Affiliation:
Universitet sparken, 8000 Aarhus C, Denmark
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study the existence problem for topological actions of finite groups on euclidean spaces Rn+k which are free outside a fixed point set Rk (embedded as a vector subspace). We refer to such an action as a semi-free action on (Rn+k, Rn) and note that all our actions will be assumed orientation-preserving.

Suppose the finite group π acts semi-freely on (Rn+k, Rn), then it acts freely on (Rn+k – Rn) = Sn–l × Rk+1. Since this space is homotopy equivalent to Sn–l, π will have periodic integral cohomology and n will be a multiple of the period. In fact the orbit space

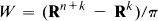
is a finitely-dominated Poincaré complex of formal dimension n – 1 with π1W = π and 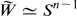as considered by Swan [41].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 4 , 01 August 1986 , pp. 781 - 860
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Anderson, D. and Pedersen, E. K., Semi-free actions of finite groups on spheres, Preprint, Odense (1982).Google Scholar
2. Bentzen, S., On the finiteness obstruction, Preprint, Aarhus University (1982).Google Scholar
3. Bentzen, S., Some numerical results on space forms, Preprint, Aarhus (1982).Google Scholar
4. Bredon, G. E., Introduction to compact transformation groups (Academic Press, New York, 1972).Google Scholar
5. Carter, D., Localizations in lower algebraic K-theory, Comm. in Algebra 8 (1980),603–622.Google Scholar
6. Carter, D., Lower K-theory of finite groups, Preprint.CrossRefGoogle Scholar
7. Cassel, J. W. S. and Fröhlich, A., Algebraic number theory (Acad. Press, New York, 1967).Google Scholar
8. Cartan, H. and Eilenberg, S., Homological algebra (Princeton University Press, N.Y., 1956).Google Scholar
9. Davis, J., Evaluation of the Swan finiteness obstruction, Thesis, Stanford (1981).Google Scholar
10. Dress, A., A characterization of solvable groups, Math. Z. 110 (1969),213–217.Google Scholar
11. Dress, A., Induction and structure theorems for orthogonal representations affinité groups, Ann. of Math. 102 (1975),291–325.Google Scholar
12. Farrell, F. T. and Hsiang, W. C, Manifolds with π1 = G × αT, Amer. J. Math. 95 (1973),813–848.Google Scholar
13. Fröhlich, A., Arithmetic and Galois modules over arithmetic orders, J. reine angew. Math. 286/287 (1916), 380–440.Google Scholar
14. Hambleton, I. and Madsen, I., Semi-free actions on R n with one fixed point, Current Trends in Algebraic Topology 1, CMS Conference Proceedings 2 (1982),89–134.Google Scholar
15. Hambleton, I. and Madsen, I., Local surgery obstructions and space forms, Preprint, I.H.E.S. (1983).Google Scholar
16. Hsiang, W. C. and Shaneson, J., Fake tori, Proceedings, Topology of Manifolds (Markham Publ. Company, Chicago, 1969).Google ScholarPubMed
17. Hodgson, J., General position in the Poincaré duality category, Invent. Math. 24 (1974),311–334.Google Scholar
18. Jones, L., Patch spaces: a geometric representation for Poincaré spaces, Ann. of Math. 97 (1973),306–343.Google Scholar
19. Laitinen, E. and Madsen, I., The L-theory of groups with periodic cohomology I, Preprint, Aarhus University (1981).Google Scholar
20. Lee, R., Semi-characteristic classes, Topology 12 (1973),183–199.Google Scholar
21. Madsen, I. Reidemeister torsion, surgery invariants and spherical space forms, Proc. LMS 46 (1983),193–240.Google Scholar
22. Madsen, I. Smooth spherical space forms, Proceedings, Evanston (1977),303–352 (Springer Lecture Notes, 657).Google Scholar
23. Milnor, J., Whitehead torsion, Bull. AMS 72 (1966),358–426.Google Scholar
24. Milnor, J., Groups which act on Sn without fixed points, Amer. J. Math. 79 (1957),623–630.Google Scholar
25. Milgram, R. J., Odd index subgroups of units in cyclotomic fields and applications, Proceedings, Evanston (1980),269–298 (Springer Lecture Notes, 854).Google Scholar
26. Milgram, R. J., Patching techniques in surgery and the solution of the compact space form problem, Preprint, Stanford University (1981).Google Scholar
27. Madsen, I., Thomas, C. B. and Wall, C. T. C., The topological spherical space form problem II, Topology 75 (1978),375–382.Google Scholar
28. Madsen, I., Thomas, C. B. and Wall, C. T. C., The topological spherical space form problem III, Smoothings and dimensional bounds, Pac. J. Math, (to appear).CrossRefGoogle Scholar
29. Maumary, S., Proper surgery groups and Wall-Novikov groups, Proceedings (Springer Lecture Notes 343, 1973),526–539.Google Scholar
30. Oliver, R., SK1 for finite group rings: II, Math. Scand. 47 (1980),195–231.Google Scholar
31. Pardon, W., Mod 2 semi-characteristic and the converse to a theorem of Milnor, Math. Z. 171 (1980), 247–268.Google Scholar
32. Pardon, W., The exact sequences of a localization for Witt groups II. Numerical invariants of odd-dimensional surgery obstructions, Pac. J. Math, (to appear).CrossRefGoogle Scholar
33. Pedersen, E. K. and Ranicki, A. A., Projective surgery theory, Topology 19 (1980),239–254.Google Scholar
34. Ranicki, A. A., Algebraic L-theory I. Foundations, Proc. LMS 27 (1973), 101–125.Google Scholar
35. Ranicki, A. A., Algebraic L-theory II. Laurent extensions, Proc. LMS 27 (1973), 126–158.Google Scholar
36. Ranicki, A. A., The algebraic theory of surgery I, Proc. LMS 40 (1980), 87–192.Google Scholar
37. Ranicki, A. A., Exact sequences in the algebraic theory of surgery, Math. Notes 26 (Princeton University Press, Princeton, 1981).Google Scholar
38. Serre, J. P., Local fields, Graduate Texts in Mathematics 67 (Springer-Verlag, New York-Heidelberg-Berlin, 1979).Google Scholar
39. Siebenmann, L., The obstruction to finding a boundary for an open manifold of dimension greater than five, Thesis, Princeton University (1965).Google Scholar
40. Siebenmann, L., A total Whitehead torsion obstruction to fibering over a circle, Comm. Math. Helv. 45 (1970), 1–48.Google Scholar
41. Swan, R., Periodic resolutions for finite groups, Ann. of Math. 72 (1960), 167–191.Google Scholar
42. Taylor, L., Surgery on paracompact manifolds, Thesis, Berkeley (1972).Google Scholar
43. Thomas, C. B. and Wall, C. T. C., On the structure of finite groups with periodic cohomology, Preprint, Liverpool University (1979).Google Scholar
44. Wall, C. T. C., The classification of hermitian forms II and III, Invent. Math. (1972), 199–141 and (1973), 59–71.Google Scholar
45. Wall, C. T. C., The classification of hermitian forms IV, Invent. Math. 23 (1974), 241–260.Google Scholar
46. Wall, C. T. C., The classification of hermitian forms VI, Ann. of Math. 103 (1976), 1–80.Google Scholar
47. Wall, C. T. C., Periodic projective resolutions, Proc. LMS 39 (1979), 509–553.Google Scholar
48. Wall, C. T. C., Norms of units in group ring, Proc. LMS 29 (1974), 593–632.Google Scholar
49. Wall, C. T. C., Foundations of algebraic L-theory, Proceedings (Springer Lecture Notes, 343, 1972).Google Scholar
50. Wolf, J., Spaces of constant curvature, 3rd. Ed. (Publish or Perish, Boston, 1977).Google Scholar