Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-05T01:29:29.694Z Has data issue: false hasContentIssue false
  • English
  • Français

Lower Radicals in Associative Rings

Published online by Cambridge University Press:  20 November 2018

J. F. Watters
J. F. Watters*
Affiliation:
The University, Leicester, England
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a homomorphically closed class of (not necessarily associative) rings 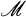, the lower radical property determined by 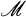is the least radical property for which all rings in 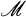are radical. Recently (7) a process of constructing the lower radical property from a class 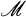of associative rings has been given which terminates after a countable number of steps. In this process, an ascending chain of classes

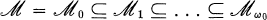
is obtained and the property of being a ring in the class 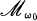is the lower radical property determined by 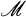. In Theorem 1 we give another characterization of the rings in the class 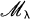, λ ∈ {1, 2, …, omega;0}, and a procedure for constructing the lower radical determined by 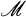in an arbitrary associative ring is given.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 466 - 476
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Anderson, T., Divinsky, N., and Sulinski, A., Hereditary radicals in associative and alternative rings, Can. J. Math. 17 (1965), 594–603.Google Scholar
2. Andrunakievic, V. A., Radicals in associative rings (1) Mat. Sb. (N.S.) U (1958), 179-212 = Amer. Math. Soc. Transi., Ser. 2, 1966, Vol. 52, pp. 95–128.Google Scholar
3. Armendariz, E. P. and Leavitt, W. G., The hereditary property in the lower radical construction, Can. J. Math. 20 (1968), 474–476.Google Scholar
4. Fuchs, L., Abelian groups (Pergamon, New York, 1960).Google Scholar
5. Heinicke, A. G., A note on lower radical constructions for associative rings, Can. Math. Bull. 11 (1968), 23–30.Google Scholar
6. Michler, G., Radikale und Sockel, Math. Ann. 167 (1966), 1–48.Google Scholar
7. Sulinski, A., Anderson, R., and Divinsky, N., Lower radical properties for associative and alternative rings, J. London Math. Soc. 41 (1966), 417–424.Google Scholar