Hostname: page-component-54dcc4c588-tfzs5 Total loading time: 0 Render date: 2025-09-19T08:02:18.467Z Has data issue: false hasContentIssue false
  • English
  • Français

Octahedral Galois Representations Arising From 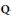$\mathbf{Q}$ -Curves of Degree 2

Published online by Cambridge University Press:  20 November 2018

J. Fernández ,
J-C. Lario  and
A. Rio
J. Fernández
Affiliation:
Departament de Matemàtica Aplicada II, Universitat Politècnica de Catalunya, Pau Gargallo 5, E-08028 Barcelona
J-C. Lario
Affiliation:
Departament de Matemàtica Aplicada II, Universitat Politècnica de Catalunya, Pau Gargallo 5, E-08028 Barcelona
A. Rio
Affiliation:
Departament de Matemàtica Aplicada II, Universitat Politècnica de Catalunya, Pau Gargallo 5, E-08028 Barcelona
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Generically, one can attach to a 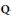$\mathbf{Q}$ -curve 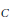$C$ octahedral representations 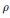$\rho $ : 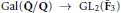$\text{Gal}\left( \mathbf{\bar{Q}}/\mathbf{Q} \right)\,\to \,\text{G}{{\text{L}}_{2}}\left( {{{\mathbf{\bar{F}}}}_{3}} \right)$ coming from the Galois action on the 3-torsion of those abelian varieties of 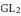$\text{G}{{\text{L}}_{2}}$ -type whose building block is 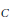$C$ . When 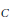$C$ is defined over a quadratic field and has an isogeny of degree 2 to its Galois conjugate, there exist such representations 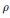$\rho $ having image into 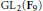$\text{G}{{\text{L}}_{2}}\left( {{\mathbf{F}}_{9}} \right)$ . Going the other way, we can ask which mod 3 octahedral representations 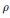$\rho $ of 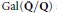$\text{Gal}\left( \mathbf{\bar{Q}}/\mathbf{Q} \right)$ arise from 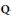$\mathbf{Q}$ -curves in the above sense. We characterize those arising from quadratic 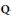$\mathbf{Q}$ -curves of degree 2. The approach makes use of Galois embedding techniques in 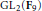$\text{G}{{\text{L}}_{2}}\left( {{\mathbf{F}}_{9}} \right)$ , and the characterization can be given in terms of a quartic polynomial defining the 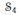${{S}_{4}}$ -extension of 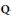$\mathbf{Q}$ corresponding to the projective representation 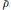$\bar{\rho }$ .

Keywords

11G0511G1011R32

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 6 , 01 December 2002 , pp. 1202 - 1228
Copyright
Copyright © Canadian Mathematical Society 2002

References

[BL99] Brunat, J. M. and Lario, J. C., Galois graphs: walks, trees and automorphisms. J. Algebraic Combin. (2) 10 (1999), 135–148.Google Scholar
[Cre98] Crespo, T., Construction of 23Sn-fields containing a C2m -field. J. Algebra (1) 201 (1998), 233–242.Google Scholar
[Cre99] Cremona, J. E., Reduction of binary, cubic and quartic forms. LMS J. Comput.Math. 2 (1999), 64–94.Google Scholar
[Elk93] Elkies, N. D., Remarks of on elliptic K-curves. 1993, preprint.Google Scholar
[ES01] Ellenberg, J. S. and Skinner, C., On the modularity of Q-curves. Duke Math. J. (1) 109 (2001), 97–122.Google Scholar
[GL98] González, J. and Lario, J. C., Rational and elliptic parametrizations of Q-curves. J. Number Theory (1) 72 (1998), 13–31.Google Scholar
[LR95] Lario, J. C. and Rio, A., An octahedral-elliptic type equality in Br2(k). C. R. Acad. Sci. Paris Sér. I. Math. (1) 321 (1995), 39–44.Google Scholar
[Py195] Pyle, E., Abelian varieties over Q with large endomorphism algebras and their simple components over Q. PhD thesis, University of California at Berkeley, 1995.Google Scholar
[Que95] Quer, J., Liftings of projective 2-dimension Galois representations and embedding problems. J. Algebra (2) 171 (1995), 541–566.Google Scholar
[Que00] Quer, J., Q-curves and abelian varieties of GL2-type. Proc. LondonMath. Soc. (3) (2) 81 (2000), 285–317.Google Scholar
[Rib76] Ribet, K. A., Galois action on division points of abelian varieties with real multiplications. Amer. J. Math. (3) 98 (1976), 751–804.Google Scholar
[Rib92] Ribet, K. A., Abelian varieties over Q and modular forms. In: Algebra and topology 1992, Taejŏn, Korea Adv. Inst. Sci. Tech., Taejŏn, 1992.Google Scholar
[Rib94] Ribet, K. A., Fields of definition of abelian varieties with real multiplication. In: Arithmetic geometry, Tempe, Arizona, 1993, Amer. Math. Soc., Providence, RI, 1994.Google Scholar
[SBT97] Shepherd-Barron, N. I. and Taylor, R., Mod 2 and mod 5 icosahedral representations. J. Amer. Math. Soc. (2) 10 (1997), 283–298.Google Scholar
[Ser77] Serre, J.-P., Modular forms of weight one and Galois representations. In: Algebraic number fields: L-functions and Galois properties, Proc. Sympos., University of Durham, Durham, 1975, Academic Press, London, 1977.Google Scholar
[Ser84] Serre, J.-P., L'invariant de Witt de la forme Tr (x2). Comment.Math. Helv. (4) 59 (1984), 651–676.Google Scholar
[Ser87] Serre, J.-P., Sur les représentations modulaires de degré 2 de Gal(Q/Q). Duke Math. J. (1) 54 (1987), 179–230.Google Scholar
[Son91] Sonn, J., Central extensions of Sn as Galois groups of regular extensions of Q(T). J. Algebra (2) 140 (1991), 355–359.Google Scholar
[Vil88] Vila, N., On stem extensions of Sn as Galois group over number fields. J. Algebra 116 (1988), 251–260.Google Scholar