Hostname: page-component-54dcc4c588-54gsr Total loading time: 0 Render date: 2025-10-07T09:05:35.090Z Has data issue: false hasContentIssue false
  • English
  • Français

On Polynomials with Curved Majorants

Published online by Cambridge University Press:  20 November 2018

D. J. Newman  and
T. J. Rivlin
D. J. Newman
Affiliation:
Temple University, Philadephia, Pennsylvania
T. J. Rivlin
Affiliation:
Watson Research Center, IBM, Yorktown Heights, New York
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A well-known result of Chebyshev is that if pn ∊ Pn , (Pn is the set of polynomials of degree at most n) and

(1)

then an(pn), the leading coefficient of pn , satisfies

(2)

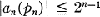
with equality holding only for pn = ±Tn , where Tn is the Chebyshev polynomial of degree n. (See [6, p. 57].) This is an example of an extremal problem in which the norm of a given linear operator on Pn is sought. Another example is A. A. Markov's result that (1) implies that

(3)

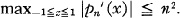
There are also results for the linear functionals pn(k) (x 0), x 0 real, k = 1, … n – 1 ([8]).

Suppose φ(x) ≧ 0 on [–1, 1] and (1) is generalized to

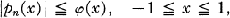
as suggested by Rahman [4] (polynomials with curved majorants), what can then be said about the analogue of (3) or similar extremal problems?

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 4 , 01 August 1982 , pp. 961 - 968
Copyright
Copyright © Canadian Mathematical Society 1982

References

References>

1. Dzjadyk, V. K., On a problem of Chebyshev and Markov, Analysis Mathematica 3 (1977), 171–175.Google Scholar
2. Lachance, M., E. B., Saft” and Varga, R. S., Inequalities for polynomials with a prescribed zero, Math. Z. 168 (1979), 105–116.Google Scholar
3. Pierre, R. and Rahman, Q. I., On a problem of Turân about polynomials, Proc. Amer. Math. Soc. 56 (1976), 231–238.Google Scholar
4. Rahman, Q. I., On a problem of Turân about polynomials with curved majorants, Trans. Amer. Math. Soc. 163 (1972), 447–455.Google Scholar
5. Rahman, Q. I., Addendum to “On a problem of Turân about polynomials with curved majorants'', Trans. Amer. Math. Soc. 168 (1972), 517–518.Google Scholar
6. Rivlin, T. J., The Chebyshev polynomials (John Wiley & Sons, New York, 1974).Google Scholar
7. Schur, I., Ûber das Maximum des absoluten Betrages eines Polynoms in einem gegebenen Interval, Math. Z. 4 (1919), 271–287.Google Scholar
8. Voronovskaja, E. V., The functional method and its applications Translations of Mathematical Monographs 28 (Amer. Math. Soc, Providence, 1970).Google Scholar