Hostname: page-component-7dd5485656-7jgsp Total loading time: 0 Render date: 2025-10-31T12:36:58.484Z Has data issue: false hasContentIssue false
  • English
  • Français

A Module-theoretic Characterization of Algebraic Hypersurfaces

Published online by Cambridge University Press:  20 November 2018

Cleto B. Miranda-Neto
Cleto B. Miranda-Neto*
Affiliation:
Departamento de Matemática, Universidade Federal da Paraíba, 58051-900 João Pessoa, PB, Brazil, e-mail: cletoneto2011@hotmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we prove the following surprising characterization: if 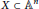$X\,\subset \,{{\mathbb{A}}^{n}}$ is an (embedded, non-empty, proper) algebraic variety deûned over a field $k$ of characteristic zero, then 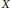$X$ is a hypersurface if and only if the module 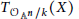${{T}_{{{O}_{{{\mathbb{A}}^{n\,/k}}}}}}(X)$ of logarithmic vector fields of 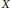$X$ is a reflexive 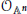${{O}_{{{\mathbb{A}}^{n}}}}$ -module. As a consequence of this result, we derive that if 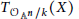${{T}_{{{O}_{{{\mathbb{A}}^{n\,/k}}}}}}(X)$ is a free 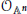${{O}_{{{\mathbb{A}}^{n}}}}$ -module, which is shown to be equivalent to the freeness of the $t$ -th exterior power of 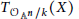${{T}_{{{O}_{{{\mathbb{A}}^{n\,/k}}}}}}(X)$ for some (in fact, any) 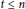$t\,\le \,n$ , then necessarily 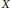$X$ is a Saito free divisor.

Keywords

14J7013N1532S2213C0513C1014N2014C2032M25hypersurfacelogarithmic vector fieldlogarithmic derivationfree divisor

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 1 , 01 March 2018 , pp. 166 - 173
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Abe, T., Terao, H., and Yoshinaga, M., Totallyfree arrangements of hyperplanes. Proc. Amer. Math. Soc. 137 (2009), no. 4, 1405–1410. http://dx.doi.org/10.1090/S0002-9939-08-09755-4.Google Scholar
[2] Aluffi, P., Chern classes offree hypersurface arrangements. J. Singul. 5 (2012), 19–32.Google Scholar
[3] Calderön-Moreno, F. and Narväez-Macarro, L., The module Tfs for locally quasi-homogeneous free divisors. Compositio Math. 134 (2002), 59–74. http://dx.doi.Org/10.1023/A:1020228824102.Google Scholar
[4] Castro-Jimenez, F. J. and Ucha-Enriquez, J. M., Logarithmic comparison theorem and some Euler homogeneous free divisors. Proc. Amer. Math. Soc. 133 (2004), 1417–1422. http://dx.doi.Org/10.1090/S0002-9939-04-07678-6.Google Scholar
[5] Cox, D. and Schenck, H., Local complete intersections in F2 and Koszul syzygies. Proc. Amer. Math. Soc. 131 (2003), 2007–2014. http://dx.doi.org/10.1090/S0002-9939-02-06804-1.Google Scholar
[6] Dämon, J., On the legaey offree divisors: discriminants and Morse-type singularities. Amer. J. Math. 120 (1998), no. 3, 453–492. http://dx.doi.org/10.1353/ajm.1998.0017.Google Scholar
[7] de Gregorio, I., Mond, D., and Sevenheck, C., Linear free divisors and Frobenius manifolds. Compos. Math. 145 (2009), no. 5, 1305–1350. http://dx.doi.Org/10.1112/S0010437X0900421 7.Google Scholar
[8] Goryunov, V., Logarithmic vectorfields for the discriminants of composite funetions. Mose. Math. J. 6 (2006), no. 1, 107–117, 122.Google Scholar
[9] Granger, M., Mond, D., and Schulze, M., Free divisors in prehomogeneous vector Spaces. Proc. Lond. Math. Soc. 102 (2011), 923–950. http://dx.doi.Org/10.1112/plms/pdqO46.Google Scholar
[10] Miranda-Neto, C. B., Graded derivation modules and algebraic free divisors. J. Pure Appl. Algebra 219 (2015), 5442–5466. http://dx.doi.Org/10.1016/j.jpaa.2015.05.026.Google Scholar
[11] Miranda-Neto, C. B., Free logarithmic derivation modules over factorial domains. Math. Res. Lett., to appear.Google Scholar
[12] Mustafa, M. and Schenck, H., The module of logarithmic p-forms ofa locallyfree arrangement. J. Algebra 241 (2001), 699–719. http://dx.doi.org/10.1006/jabr.2000.8606.Google Scholar
[13] Saito, K., Theory of logarithmic differential forms and logarithmic vectorfields. J. Fac. Sei. Univ. Tokyo Sect. IA Math. 27 (1980), 265–291.Google Scholar
[14] Samuel, P., Anneaux gradues factoriels et modules reflexifs. Bull. Soc. Math. France 92 (1964), 237–249.Google Scholar
[15] Schenck, H., Terao, H., and Yoshinaga, M., Logarithmic vectorfields for curve configurations in F2 with quasihomogeneous singularities. Math. Res. Lett., to appear.Google Scholar
[16] Schenck, H. and Tohaneanu, S., Freeness of conic-line arrangements in F2. Comment. Math. Helv. 84 (2009), no. 2, 235–258. http://dx.doi.org/10.4171/CMH/161.Google Scholar
[17] Seibt, P., Differential filtrations and symbolic powers of regulär primes. Math. Z. 166 (1979), 159–164. http://dx.doi.Org/10.1007/BF01 214042.Google Scholar
[18] Seidenberg, A., Differential Ideals in rings offinitely generated type. Amer. J. Math. 89 (1967), 22–42. http://dx.doi.org/10.2307/2373093.Google Scholar
[19] Sekiguchi, J., A classification of weighted homogeneous Saito free divisors. J. Math. Soc. Japan 61 (2009), 1071–1095. http://dx.doi.org/10.2969/jmsj706141071.Google Scholar
[20] Simis, A. and Tohaneanu, S., Homology of homogeneous divisors. Israel J. Math. 200 (2014), 449–487. http://dx.doi.Org/10.1007/s11856-014-0025-3.Google Scholar
[21] Simis, A. and Ulrich, B., The Fitting ideal problem. Bull. Lond. Math. Soc. 41 (2009), 79–88. http://dx.doi.Org/1 0.1112/blms/bdn106.Google Scholar
[22] Terao, H., Arrangements of hyperplanes and their freeness. I, II. J. Fac. Sei. Univ. Tokyo Sect. IA Math. 27 (1980), 293–320.Google Scholar
[23] Terao, H., Generalized exponents ofafree arrangement of hyperplanes and Shephard-Todd-Brieskorn formula. Invent. Math. 63 (1981), 159–179. http://dx.doi.Org/1 0.1007/BF01389197.Google Scholar
[24] Traves, W. and Wakeneid, M., Derivation radical subspace arrangements. J. Pure Appl. Algebra 215 (2011), 1492–1501. http://dx.doi.Org/10.1016/j.jpaa.2010.09.007.Google Scholar
[25] Yoshinaga, M., Characterization ofafree arrangement and conjeeture ofEdelman and Reiner. Invent. Math. 157 (2004), 449–454. http://dx.doi.Org/10.1007/s00222-004-0359-2.Google Scholar
[26] Yoshinaga, M., On the freeness of3-arrangements. Bull. London Math. Soc. 37 (2005), 126–134. http://dx.doi.org/10.1112/S0024609304003704Google Scholar