Hostname: page-component-76c49bb84f-6sxsx Total loading time: 0 Render date: 2025-07-13T13:05:14.721Z Has data issue: false hasContentIssue false
  • English
  • Français

Quantum Unique Ergodicity on Locally Symmetric Spaces: the Degenerate Lift

Published online by Cambridge University Press:  20 November 2018

Lior Silberman
Lior Silberman*
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC, V6T 1Z2 e-mail: lior@math.ubc.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a measure 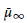${{\bar{\mu }}_{\infty }}$ on a locally symmetric space 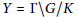$Y=\Gamma \backslash G/K$ obtained as a weak-$*$ limit of probability measures associated with eigenfunctions of the ring of invariant differential operators, we construct a measure 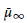${{\bar{\mu }}_{\infty }}$ on the homogeneous space 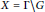$X=\Gamma \backslash G$ that lifts 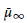${{\bar{\mu }}_{\infty }}$ and is invariant by a connected subgroup 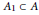${{A}_{1}}\subset A$ of positive dimension, where 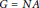$G=NAK$ is an Iwasawa decomposition. If the functions are, in addition, eigenfunctions of the Hecke operators, then 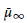${{\bar{\mu }}_{\infty }}$ is also the limit of measures associated with Hecke eigenfunctions on $X$. This generalizes results of the author with A. Venkatesh in the case where the spectral parameters stay away from the walls of the Weyl chamber.

Keywords

22E5043A85quantum unique ergodicitymicrolocal liftspherical dual

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 3 , 01 September 2015 , pp. 632 - 650
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Anantharaman, N., Entropy and the localization of eigenfunctions. Ann. of Math.(2) 168(2008), no. 2, 435–475. http://dx.doi.Org/1 0.4007/annals.2008.1 68.435 Google Scholar
[2] Anantharaman, N. and Silberman, L., A Haar component for quantum limits on locally symmetric spaces. Israel J. Math. 195(2013), no. 1, 393–447. http://dx.doi.Org/10.1007/s11 856-012-0133-x Google Scholar
[3] Anantharaman, N. and Zelditch, S., Patterson-Sullivan distributions and quantum ergodicity. Ann. Henri Poincaré 8(2007), no. 2,361–426. http://dx.doi.org/10.1007/s00023-006-0311-7 Google Scholar
[4] Arthur, J., Intertwining operators and residues. I. Weighted characters. J. Funct. Anal. 84(1989), no. 1, 19–84. http://dx.doi.Org/10.101 6/0022-1236(89)90110-9 Google Scholar
[5] Bourgain, J. and Lindenstrauss, E., Entropy of quantum limits. Comm. Math. Phys. 233(2003), no. 1, 153–171. http://dx.doi.org/10.1007/s00220-002-0770-8 Google Scholar
[6] Colin de Verdière, Y., Ergodicité et fonctions propres du laplacien. Comm. Math. Phys. 102(1985), no. 3, 497–502. http://dx.doi.org/10.1007/BF01209296 Google Scholar
[7] Einsiedler, M. and Lindenstrauss, E., Onmeasures invariant under diagonalizable actions: the rank-one case and the general low-entropy method. J. Mod. Dyn. 2(2008), no. 1, 83–128.Google Scholar
[8] Evans, L. C. and Zworski, M., Lectures on semiclassical analysis, (version 0.2) http://math.berkeley.edu/-evans/sem iclassical.pdf Google Scholar
[9] Hansen, S., Hilgert, J., and Schroder, M., Patterson-Sullivan distributions in higher rank. Math. Z. 272(2012), no. 1-2, :607-643. http://dx.doi.org/10.1007/s00209-011-0952-1 Google Scholar
[10] Knapp, A. W. and Stein, E. M., Intertwining operators for semisimple groups. Ann. of Math.(2) 93(1971), 489–578. http://dx.doi.Org/10.2307/1 970887 Google Scholar
[11] Knapp, A. W., Representation theory of semisimple groups. An overview based on examples. Princeton Mathematical Series, 36, Princeton University Press, Princeton, NJ, 1986.Google Scholar
[12] Lindenstrauss, E., On quantum unique ergodicity for F\H x H. Internat. Math. Res. Notices 2001, no. 17, 913–933.Google Scholar
[13] Lindenstrauss, E. , Invariant measures and arithmetic quantum unique ergodicity. Ann. of Math.(2) 163(2006), 165–219. http://dx.doi.org/10.4007/annals.2006.163.165 Google Scholar
[14] Maucourant, F., A nonhomogeneous orbit closure of a diagonal subgroup. Ann. of Math.(2) 171(2010), no. 1, 557–570. http://dx.doi.org/10.4007/annals.2010.171.557 Google Scholar
[15] Rudnick, Z. and Sarnak, P., The behaviour of eigenstates of arithmetic hyperbolic manifolds. Comm. Math. Phys. 161(1994), no. 1, 195–213. http://dx.doi.Org/10.1007/BF0209941 8 Google Scholar
[16] Silberman, L. and Venkatesh, A., Entropy bounds for Heckeeigenfunctions on division algebras. In revision.Google Scholar
[17] Silberman, L. and Venkatesh, A. , Quantum unique ergodicity for locally symmetric spaces. Geom. Funct. Anal. 17(2007), no. 3, 960–998. http://dx.doi.Org/1 0.1007/s00039-007-0611 -1 Google Scholar
[18] ShnireFman, A. I., Ergodic properties of eigenfunctions. Uspekhi Mat. Nauk. 29(1974), no. 6(180), 181–182.Google Scholar
[19] Soundararajan, K., Quantum unique ergodicity for SL2(Z)\HL Ann. of Math. (2) 172(2010), no. 2, 1529–1538.Google Scholar
[20] Wolpert, S. A., Semiclassical limits for the hyperbolic plane. Duke Math. J. 108(2001), no. 3, 449–509. http://dx.doi.Org/10.1215/S0012-7094-01-10833-8 Google Scholar
[21] Zelditch, S., Pseudodifferential analysis on hyperbolic surfaces. J. Funct. Anal. 68(1986), no. 1, 72–105. http://dx.doi.Org/1 0.101 6/0022-1236(86)90058-3 Google Scholar
[22] Zelditch, S., Uniform distribution of eigenfunctions on compact hyperbolic surfaces. Duke Math. J. 55(1987), no. 4, 919–941. http://dx.doi.org/10.1215/S0012-7094-87-05546-3 Google Scholar
[23] Zelditch, S., The averaging method and ergodic theory for pseudo-differential operators on compact hyperbolic surfaces. J. Funct. Anal. 82(1989), 38–68. http://dx.doi.org/! 0.101 6/0022-1236(89)90091 -8 Google Scholar