Embedding theorems for random graphs with specified degrees

Abstract

Given an 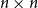$n\times n$ symmetric matrix 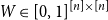$W\in [0,1]^{[n]\times [n]}$, let 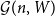${\mathcal G}(n,W)$ be the random graph obtained by independently including each edge 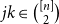$jk\in \binom{[n]}{2}$ with probability 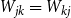$W_{jk}=W_{kj}$. Given a degree sequence 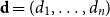$\textbf{d}=(d_1,\ldots, d_n)$, let 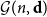${\mathcal G}(n,\textbf{d})$ denote a uniformly random graph with degree sequence 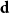$\textbf{d}$. We couple 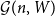${\mathcal G}(n,W)$ and 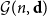${\mathcal G}(n,\textbf{d})$ together so that asymptotically almost surely 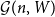${\mathcal G}(n,W)$ is a subgraph of ${\mathcal G}(n,\textbf{d})$, where 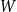$W$ is some function of 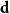$\textbf{d}$. Let $\Delta (\textbf{d})$ denote the maximum degree in 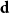$\textbf{d}$. Our coupling result is optimal when 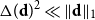$\Delta (\textbf{d})^2\ll \|\textbf{d}\|_1$, that is, 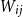$W_{ij}$ is asymptotic to ${\mathbb P}(ij\in{\mathcal G}(n,\textbf{d}))$ for every 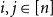$i,j\in [n]$. We also have coupling results for 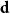$\textbf{d}$ that are not constrained by the condition $\Delta (\textbf{d})^2\ll \|\textbf{d}\|_1$. For such $\textbf{d}$ our coupling result is still close to optimal, in the sense that 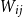$W_{ij}$ is asymptotic to 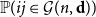${\mathbb P}(ij\in{\mathcal G}(n,\textbf{d}))$ for most pairs $ij\in \binom{[n]}{2}$.