Hostname: page-component-7dd5485656-dk7s8 Total loading time: 0 Render date: 2025-10-29T21:46:50.563Z Has data issue: false hasContentIssue false
  • English
  • Français

Hypergraphs without non-trivial intersecting subgraphs

Part of: Extremal combinatorics Graph theory

Published online by Cambridge University Press:  09 June 2022

Xizhi Liu
Xizhi Liu*
Affiliation:
Department of Mathematics, Statistics, and Computer Science, University of Illinois, Chicago, IL, 60607 USA
*
Email: xliu246@uic.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A hypergraph 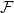$\mathcal{F}$ is non-trivial intersecting if every pair of edges in it have a nonempty intersection, but no vertex is contained in all edges of 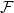$\mathcal{F}$. Mubayi and Verstraëte showed that for every 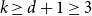$k \ge d+1 \ge 3$ and 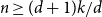$n \ge (d+1)k/d$ every 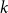$k$-graph 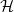$\mathcal{H}$ on $n$ vertices without a non-trivial intersecting subgraph of size 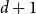$d+1$ contains at most 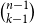$\binom{n-1}{k-1}$ edges. They conjectured that the same conclusion holds for all 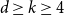$d \ge k \ge 4$ and sufficiently large $n$. We confirm their conjecture by proving a stronger statement.

They also conjectured that for 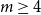$m \ge 4$ and sufficiently large $n$ the maximum size of a 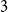$3$-graph on $n$ vertices without a non-trivial intersecting subgraph of size 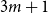$3m+1$ is achieved by certain Steiner triple systems. We give a construction with more edges showing that their conjecture is not true in general.

Keywords

hypergraphsextremal set theoryintersecting family

MSC classification

Primary: 05D05: Extremal set theory
Secondary: 05C65: Hypergraphs 05C69: Dominating sets, independent sets, cliques

Information

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 6 , November 2022 , pp. 1076 - 1091
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

*

Research partially supported by NSF award DMS-1763317.

References

Bermond, J.-C. and Frankl, P. (1977) On a conjecture of Chvátal on $m$ -intersecting hypergraphs. Bull. London Math. Soc. 9(3) 310–312.CrossRefGoogle Scholar
Chvátal, V. (1974/75) An extremal set-intersection theorem. J. London Math. Soc. (2) 9 355–359.CrossRefGoogle Scholar
Csákány, R. and Kahn, J. (1999) A homological approach to two problems on finite sets. J. Algebraic Combin. 9(2) 141–149.CrossRefGoogle Scholar
Currier, G. (2021) New results on simplex-clusters in set systems. Combinatorica 41(4) 495–506.CrossRefGoogle Scholar
Erdős, P. (1971) Topics in combinatorial analysis. In Proceedings of the Second Louisiana Conference on Combinatorics, Graph Theory and Computing, pp.2–20.Google Scholar
Frankl, P. (1976) On Sperner families satisfying an additional condition. J. Combin. Theory Ser. A 20(1) 1–11.CrossRefGoogle Scholar
Frankl, P. (1981) On a problem of Chvátal and Erdős on hypergraphs containing no generalized simplex. J. Combin. Theory Ser. A 30(2) 169–182.CrossRefGoogle Scholar
Frankl, P. and Füredi, Z. (1985) Forbidding just one intersection. J. Combin. Theory Ser. A 39(2) 160–176.CrossRefGoogle Scholar
Frankl, P. and Füredi, Z. (1987) Exact solution of some Turán-type problems. J. Combin. Theory Ser. A 45(2) 226–262.CrossRefGoogle Scholar
Füredi, Z. (1983) On finite set-systems whose every intersection is a kernel of a star. Discrete Math. 47(1) 129–132.CrossRefGoogle Scholar
Füredi, Z. and Özkahya, L. (2011) Unavoidable subhypergraphs: $\bf a$ -clusters. J. Combin. Theory Ser. A 118(8) 2246–2256.CrossRefGoogle Scholar
Katona, G. (1968) A theorem of finite sets. In Theory of Graphs (Proc. Colloq., Tihany, 1966), pp.187–207.Google Scholar
Keevash, P. (2018) The existence of designs II. arXiv preprint arXiv: 1802. 05900.Google Scholar
Keevash, P. and Mubayi, D. (2010) Set systems without a simplex or a cluster. Combinatorica 30(2) 175–200.CrossRefGoogle Scholar
Keller, N. and Lifshitz, N. (2021) The junta method for hypergraphs and the Erdős-Chvátal simplex conjecture. Adv. Math 392(Paper No. 107991) 95.CrossRefGoogle Scholar
Kostochka, A. and Mubayi, D. (2017) The structure of large intersecting families. Proc. Amer. Math. Soc. 145(6) 2311–2321.CrossRefGoogle Scholar
Kruskal, J. B. (1963) The number of simplices in a complex . In Mathematical Optimization Techniques. Univ. California Press, pp. 251–278.CrossRefGoogle Scholar
Lifshitz, N. (2020) On set systems without a simplex-cluster and the junta method. J. Combin. Theory Ser. A 170(105139) 20.CrossRefGoogle Scholar
Lovász, L. (1993) Combinatorial Problems and Exercises, Second edition. North-Holland Publishing Co. Google Scholar
Mantel, W. (1907) Problem 28. Wiskundige Opgaven 10(60-61) 320.Google Scholar
Mubayi, D. and Verstraëte, J. (2005) Proof of a conjecture of Erdős on triangles in set-systems. Combinatorica 25(5) 599–614.CrossRefGoogle Scholar
Rödl, V., Ruciński, A. and Szemerédi, E. (2006) Perfect matchings in uniform hypergraphs with large minimum degree. European J. Combin. 27(8) 1333–1349.CrossRefGoogle Scholar