Hostname: page-component-7dd5485656-zklqj Total loading time: 0 Render date: 2025-10-31T03:38:00.406Z Has data issue: false hasContentIssue false
  • English
  • Français

Large N behaviour of the two-dimensional Yang–Mills partition function

Part of: Abstract harmonic analysis Quantum field theory; related classical field theories

Published online by Cambridge University Press:  30 June 2021

Thibaut Lemoine
Thibaut Lemoine*
Affiliation:
Institut de Recherche Mathématique Avancée, UMR 7501, Université de Strasbourg et CNRS, 7 rue René Descartes, 67000 Strasbourg, France Email: thibaut.lemoine@unistra.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We compute the large N limit of the partition function of the Euclidean Yang–Mills measure on orientable compact surfaces with genus 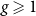$g\geqslant 1$ and non-orientable compact surfaces with genus 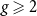$g\geqslant 2$, with structure group the unitary group 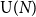${\mathrm U}(N)$ or special unitary group 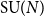${\mathrm{SU}}(N)$. Our proofs are based on asymptotic representation theory: more specifically, we control the dimension and Casimir number of irreducible representations of 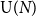${\mathrm U}(N)$ and 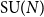${\mathrm{SU}}(N)$ when N tends to infinity. Our main technical tool, involving ‘almost flat’ Young diagram, makes rigorous the arguments used by Gross and Taylor (1993, Nuclear Phys. B 400(1–3) 181–208) in the setting of QCD, and in some cases, we recover formulae given by Douglas (1995, Quantum Field Theory and String Theory (Cargèse, 1993), Vol. 328 of NATO Advanced Science Institutes Series B: Physics, Plenum, New York, pp. 119–135) and Rusakov (1993, Phys. Lett. B 303(1) 95–98).

Keywords

Two-dimensional Yang–Mills theorylarge N limitasymptotic representation theoryWitten zeta functionalmost flat highest weights

MSC classification

Primary: 43A75: Analysis on specific compact groups 81T13: Yang-Mills and other gauge theories

Information

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 1 , January 2022 , pp. 144 - 165
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Anshelevich, M. and Sengupta, A. N. (2012) Quantum free Yang–Mills on the plane. J. Geom. Phys. 62(2) 330–343.CrossRefGoogle Scholar
Boutet de Monvel, A. and Shcherbina, M. (1998) On free energy in two-dimensional ${\rm U}(n)$ -gauge field theory on the sphere. Teoret. Mat. Fiz. 115(3) 389–401.Google Scholar
Bröcker, T. and tom Dieck, T. (1995) Representations of compact Lie groups , Vol. 98 of Graduate Texts in Mathematics. Springer-Verlag, New York.Google Scholar
Dahlqvist, A. and Norris, J. (2017) Yang–Mills measure and the master field on the sphere. arXiv preprint: https://arxiv.org/abs/1703.10578.Google Scholar
Douglas, M. R. and Kazakov, V. A. (1993) Large N phase transition in continuum QCD ${}_2$ . Phys. Lett. B 319 219–230.CrossRefGoogle Scholar
Douglas, M. R. (1995) Conformal field theory techniques in large N Yang-Mills theory. In Quantum Field Theory and String Theory (Cargèse, 1993), Vol. 328 of NATO Advanced Science Institutes Series B: Physics, Plenum, New York, pp. 119–135.CrossRefGoogle Scholar
Driver, B. K., Gabriel, F., Hall, B. C. and Kemp, T. (2017) The Makeenko-Migdal equation for Yang-Mills theory on compact surfaces. Comm. Math. Phys. 352(3) 967–978.CrossRefGoogle Scholar
Forrester, P. J., Majumdar, S. N. and Schehr, G. (2011) Non-intersecting Brownian walkers and Yang–Mills theory on the sphere. Nuclear Phys. B 844(3) 500–526.CrossRefGoogle Scholar
Fulton, W. and Harris, J. (1991) Representation Theory, Vol. 129 of Graduate Texts in Mathematics. Springer-Verlag, New York. A first course, Readings in Mathematics.Google Scholar
Gross, D. J. (1993) Two-dimensional QCD as a string theory. Nuclear Phys. B 400(1–3) 161–180.CrossRefGoogle Scholar
Gross, D. J. and Matytsin, A. (1995) Some properties of large-N two-dimensional Yang-Mills theory. Nuclear Phys. B 437(3) 541–584.CrossRefGoogle Scholar
Gross, D. J. and Taylor, IV, W. (1993) Two-dimensional QCD is a string theory. Nuclear Phys. B 400(1–3) 181–208.CrossRefGoogle Scholar
Guionnet, A. and Maïda, M. (2005) Character expansion method for the first order asymptotics of a matrix integral. Probab. Theory Related Fields 132(4) 539–578.CrossRefGoogle Scholar
Hall, B. C. (2018) The large-N limit for two-dimensional Yang–Mills theory. Comm. Math. Phys. 363(3) 789–828.CrossRefGoogle Scholar
Hooft, G. (1974) A planar diagram theory for strong interactions. Nuclear Phys. B 72(3) 461–473.CrossRefGoogle Scholar
Lévy, T. (2003) Yang-Mills measure on compact surfaces. Mem. Am. Math. Soc. 166(790) xiv+122.CrossRefGoogle Scholar
Lévy, T. (2017) The master field on the plane. Astérisque 388 ix+201.Google Scholar
Lévy, T. and Maïda, M. (2015) On the Douglas-Kazakov phase transition. Weighted potential theory under constraint for probabilists. In Modélisation Aléatoire et Statistique—Journées MAS 2014, Vol. 51 of ESAIM Proceedings and Surveys, EDP Sciences, Les Ulis, pp. 89–121.CrossRefGoogle Scholar
Massey, W. S. (1991) A Basic Course in Algebraic Topology , Vol. 127 of Graduate Texts in Mathematics. Springer-Verlag, New York.Google Scholar
Rusakov, B. (1993) Large-N quantum gauge theories in two dimensions. Phys. Lett. B 303(1) 95–98.CrossRefGoogle Scholar
Sengupta, A. (1992) The Yang-Mills measure for $S^2$ . J. Funct. Anal. 108(2) 231–273.CrossRefGoogle Scholar
Sengupta, A. (1997) Yang-Mills on surfaces with boundary: quantum theory and symplectic limit. Comm. Math. Phys. 183(3) 661–705.CrossRefGoogle Scholar
Sengupta, A. N. (2008) Gauge theory in two dimensions: topological, geometric and probabilistic aspects. In Stochastic Analysis in Mathematical Physics, World Scientific Publishing, Hackensack, NJ, pp. 109–129.Google Scholar
Sengupta, A. N. (2008) Traces in two-dimensional QCD: the large-N limit. In Traces in Number Theory, Geometry and Quantum Fields, Vol. E38 of Aspects of Mathematics, Friedrich Vieweg, Wiesbaden, pp. 193–212.Google Scholar
Stanley, R. P. (1999) Enumerative Combinatorics. Vol. 2 , Vol. 62 of Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge.Google Scholar
Tate, T. and Zelditch, S. (2003) Counterexample to conjectured SU(N) character asymptotics. arXiv preprint: https://arxiv.org/abs/hep-th/0310149.Google Scholar
Vershik, A. M. and Okounkov, A. Yu. (2004) A new approach to representation theory of symmetric groups. II. Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 307(Teor. Predst. Din. Sist. Komb. i Algoritm. Metody. 10) 57–98, 281.Google Scholar
Witten, E. (1991) On quantum gauge theories in two dimensions. Comm. Math. Phys. 141(1) 153–209.CrossRefGoogle Scholar
Zagier, D. (1994) Values of zeta functions and their applications. In First European Congress of Mathematics, Vol. II (Paris, 1992), Vol. 120 of Progress in Mathematics, Birkhäuser, Basel, pp. 497–512.CrossRefGoogle Scholar
Zelditch, S. (2004) Macdonald’s identities and the large N limit of $\rm YM_2$ on the cylinder. Comm. Math. Phys. 245(3) 611–626.CrossRefGoogle Scholar