Hostname: page-component-7dd5485656-2pp2p Total loading time: 0 Render date: 2025-10-30T16:28:32.384Z Has data issue: false hasContentIssue false
  • English
  • Français

Many Hamiltonian subsets in large graphs with given density

Part of: Graph theory

Published online by Cambridge University Press:  02 October 2023

Stijn Cambie Open the ORCID record for Stijn Cambie [Opens in a new window] ,
Jun Gao  and
Hong Liu Open the ORCID record for Hong Liu [Opens in a new window]
Stijn Cambie*
Affiliation:
Institute for Basic Science (IBS), Daejeon, South Korea Department of Computer Science, KU Leuven Campus Kulak-Kortrijk, Kortrijk, Belgium.
Jun Gao
Affiliation:
Institute for Basic Science (IBS), Daejeon, South Korea
Hong Liu
Affiliation:
Institute for Basic Science (IBS), Daejeon, South Korea
*
Corresponding author: Stijn Cambie; Email: stijn.cambie@hotmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

A set of vertices in a graph is a Hamiltonian subset if it induces a subgraph containing a Hamiltonian cycle. Kim, Liu, Sharifzadeh, and Staden proved that for large 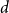$d$, among all graphs with minimum degree 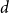$d$, 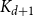$K_{d+1}$ minimises the number of Hamiltonian subsets. We prove a near optimal lower bound that takes also the order and the structure of a graph into account. For many natural graph classes, it provides a much better bound than the extremal one (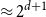$\approx 2^{d+1}$). Among others, our bound implies that an $n$-vertex 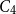$C_4$-free graph with minimum degree 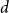$d$ contains at least 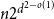$n2^{d^{2-o(1)}}$ Hamiltonian subsets.

Keywords

Hamiltonian cyclescruxKomlós conjecture

MSC classification

Primary: 05C35: Extremal problems
Secondary: 05C38: Paths and cycles

Information

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 33 , Issue 1 , January 2024 , pp. 110 - 120
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

*

Supported by the Institute for Basic Science (IBS-R029-C4).

†

Supported by Internal Funds of KU Leuven (PDM fellowship PDMT1/22/005).

References

Alon, N. and Chung, F. R. K. (1988) Explicit construction of linear sized tolerant networks. In Proceedings of the First Japan Conference on Graph Theory and Applications (Hakone, 1986), pp. 15–19, Vol. 72.Google Scholar
Csaba, B., Kühn, D., Lo, A., Osthus, D. and Treglown, A. (2016) Proof of the 1-Factorization and Hamilton Decomposition Conjectures. American Mathematical Society, Vol. 244.Google Scholar
Dirac, G. A. (1952) Some theorems on abstract graphs. Proc. Lond. Math. Soc. 3(1) 69–81.Google Scholar
Fernández, I. G., Hyde, J., Liu, H., Pikhurko, O. and Wu, Z. (2023) Disjoint isomorphic balanced clique subdivisions. J. Combin. Theory Ser. B 161 417–436.Google Scholar
Fernández, I. G., Kim, J., Kim, Y. and Liu, H. (2022) Nested cycles with no geometric crossings. Proc. Am. Math. Soc. Ser. B 9(3) 22–32.Google Scholar
Friedman, L. and Krivelevich, M. (2021) Cycle lengths in expanding graphs. Combinatorica 41(1) 53–74.Google Scholar
Gil Fernández, I. and Liu, H. (2023) How to build a pillar: a proof of Thomassen’s conjecture. J. Combin. Theory Ser. B 162 13–33.Google Scholar
Haslegrave, J., Hu, J., Kim, J., Liu, H., Luan, B. and Wang, G. (2022) Crux and long cycles in graphs. SIAM J. Discrete Math. 36(4) 2942–2958.Google Scholar
Haslegrave, J., Hyde, J., Kim, J. and Liu, H. (2023) Ramsey numbers of cycles versus general graphs. Forum Math. Sigma 11, Paper No. e10, 18.Google Scholar
Haslegrave, J., Kim, J. and Liu, H. (2022) Extremal density for sparse minors and subdivisions. Int. Math. Res. Not. IMRN 20(20) 15505–15548.Google Scholar
Im, S., Kim, J., Kim, Y. and Liu, H. (2023) Crux, space constraints and subdivisions. arXiv preprint, arXiv: 2207.06653.Google Scholar
Karp, R. M. (1972) Reducibility among combinatorial problems. In Complexity of Computer Computations, Springer, pp. 85–103.Google Scholar
Kim, J., Liu, H., Sharifzadeh, M. and Staden, K. (2017) Proof of Komlós’s conjecture on Hamiltonian subsets. Proc. Lond. Math. Soc. 115(5) 974–1013.Google Scholar
Knox, F., Kühn, D. and Osthus, D. (2015) Edge-disjoint Hamilton cycles in random graphs. Random Struct. Algorithms 46(3) 397–445.Google Scholar
Komlós, J. and Szemerédi, E. (1994) Topological cliques in graphs. Combin. Probab. Comput. 3(2) 247–256.Google Scholar
Komlós, J. and Szemerédi, E. (1996) Topological cliques in graphs. II. Combin. Probab. Comput. 5(1) 79–90.Google Scholar
Krivelevich, M. (2019) Long cycles in locally expanding graphs, with applications. Combinatorica 39(1) 135–151.Google Scholar
Kühn, D. and Osthus, D. (2013) Hamilton decompositions of regular expanders: a proof of Kelly’s conjecture for large tournaments. Adv. Math. 237 62–146.Google Scholar
Kühn, D. and Osthus, D. (2014) Hamilton cycles in graphs and hypergraphs: an extremal perspective. In Proceedings of the International Congress of Mathematicians—Seoul 2014. Vol. IV, Kyung Moon Sa, Seoul, pp. 381–406.Google Scholar
Kühn, D. and Osthus, D. (2014) Hamilton decompositions of regular expanders: applications. J. Combin. Theory Ser. B 104 1–27.Google Scholar
Kühn, D., Osthus, D. and Taraz, A. (2005) Large planar subgraphs in dense graphs. J. Combin. Theory Ser. B 95(2) 263–282.CrossRefGoogle Scholar
Liu, H. and Montgomery, R. (2017) A proof of Mader’s conjecture on large clique subdivisions in $C_4$ -free graphs. J. Lond. Math. Soc. 95(1) 203–222.Google Scholar
Liu, H. and Montgomery, R. (2023) A solution to Erdős and Hajnal’s odd cycle problem. J. Am. Math. Soc. 36(4) 1191–1234.Google Scholar
Liu, H., Wang, G. and Yang, D. (2022) Clique immersion in graphs without a fixed bipartite graph. J. Combin. Theory Ser. B 157 346–365.Google Scholar