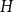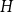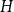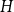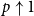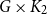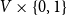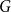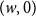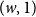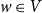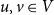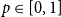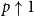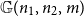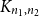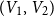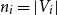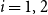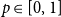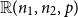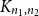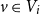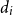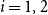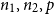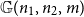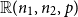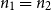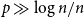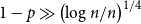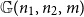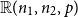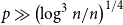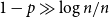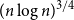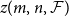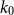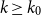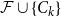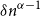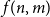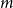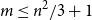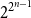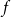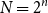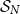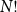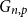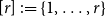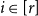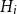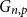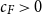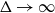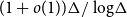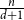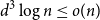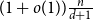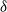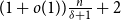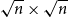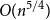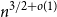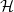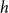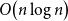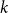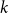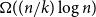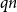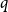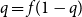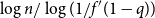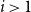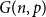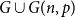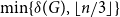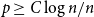Contents
Paper
Ramsey upper density of infinite graphs
- Part of:
-
- Published online by Cambridge University Press:
- 25 April 2023, pp. 703-723
-
- Article
- Export citation
The bunkbed conjecture holds in the
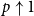 $p\uparrow 1$ limit
$p\uparrow 1$ limit
- Part of:
-
- Published online by Cambridge University Press:
- 14 December 2022, pp. 363-369
-
- Article
- Export citation
Sandwiching biregular random graphs
- Part of:
-
- Published online by Cambridge University Press:
- 06 June 2022, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unimodular random one-ended planar graphs are sofic
- Part of:
-
- Published online by Cambridge University Press:
- 09 June 2023, pp. 851-858
-
- Article
- Export citation
Bipartite-ness under smooth conditions
- Part of:
-
- Published online by Cambridge University Press:
- 03 February 2023, pp. 546-558
-
- Article
- Export citation
Degree sequences of sufficiently dense random uniform hypergraphs
- Part of:
-
- Published online by Cambridge University Press:
- 15 August 2022, pp. 183-224
-
- Article
- Export citation
Maximal chordal subgraphs
- Part of:
-
- Published online by Cambridge University Press:
- 02 May 2023, pp. 724-741
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Brownian bridge expansions for Lévy area approximations and particular values of the Riemann zeta function
- Part of:
-
- Published online by Cambridge University Press:
- 03 November 2022, pp. 370-397
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random feedback shift registers and the limit distribution for largest cycle lengths
- Part of:
-
- Published online by Cambridge University Press:
- 14 February 2023, pp. 559-593
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Towards the 0-statement of the Kohayakawa-Kreuter conjecture
- Part of:
-
- Published online by Cambridge University Press:
- 27 September 2022, pp. 225-268
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Colouring graphs with forbidden bipartite subgraphs
- Part of:
-
- Published online by Cambridge University Press:
- 08 June 2022, pp. 45-67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Archaeology of random recursive dags and Cooper-Frieze random networks
- Part of:
-
- Published online by Cambridge University Press:
- 13 June 2023, pp. 859-873
-
- Article
- Export citation
On random walks and switched random walks on homogeneous spaces
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2022, pp. 398-421
-
- Article
- Export citation
Irregular subgraphs
- Part of:
-
- Published online by Cambridge University Press:
- 23 September 2022, pp. 269-283
-
- Article
- Export citation
On the size-Ramsey number of grids
- Part of:
-
- Published online by Cambridge University Press:
- 26 June 2023, pp. 874-880
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Universal geometric graphs
- Part of:
-
- Published online by Cambridge University Press:
- 15 May 2023, pp. 742-761
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiple random walks on graphs: mixing few to cover many
- Part of:
-
- Published online by Cambridge University Press:
- 15 February 2023, pp. 594-637
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the peel number and the leaf-height of Galton–Watson trees
- Part of:
-
- Published online by Cambridge University Press:
- 09 June 2022, pp. 68-90
-
- Article
- Export citation
Triangles in randomly perturbed graphs
- Part of:
-
- Published online by Cambridge University Press:
- 05 July 2022, pp. 91-121
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Supercritical site percolation on the hypercube: small components are small
- Part of:
-
- Published online by Cambridge University Press:
- 25 November 2022, pp. 422-427
-
- Article
-
- You have access
- Open access
- HTML
- Export citation