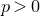1. Introduction
The birational part of Grothendieck’s anabelian geometry, and its close relative known as Bogomolov’s programme, are concerned with recovering fields (say finitely generated over a prime field or an algebraically closed field) from their absolute Galois groups or certain quotients thereof. See, for instance, [Reference Neukirch, Schmidt and WingbergNSW08, Chapter XII, § 3] and [Reference SzamuelySza04, § 2] for an overview. An important step in most approaches to such reconstruction questions consists in first developing a local theory, i.e. recovering the decomposition groups of certain valuations from the given Galois group; see, for instance, [Reference SzamuelySza04, § 3] (commenting on [Reference PopPop94]) and [Reference PopPop12] (also for its historical notes). An illustration of this appeared in [Reference NeukirchNeu69], preceding the formulation of the conjectures of anabelian geometry, which studies the characterisation of number fields by their absolute Galois groups. Here a Galois-theoretic characterisation of algebraic p-adic numbers and their finite extensions is given. (See also the presentation in [Reference Neukirch, Schmidt and WingbergNSW08, Chapter XII, §§ 1–2].)
By now there exists a substantial body of work concerning the valuation-theoretic consequences of Galois-theoretic input data; see, for instance, the textbook presentations [Reference Engler and PrestelEP05, § 5.4] and [Reference EfratEfr06, Chapter 26] (both ultimately relying on the technique of rigid elements going back to [Reference WareWar81, Reference Arason, Elman and JacobAEJ87]) and the literature referenced there. Arguably, one of the most satisfying results in this regard is the complete characterisation of the class of p-adically closed fields (a well-behaved class containing the p-adic numbers as well as their finite extensions and their algebraic parts) in terms of their Galois group [Reference PopPop88, Reference EfratEfr95, Reference KoenigsmannKoe95], in a generalisation of [Reference NeukirchNeu69, Theorem 1], and in strong analogy to the Galois-theoretic characterisation of real-closed fields [Reference Artin and SchreierAS27]. This result for p-adically closed fields in turn has consequences for the section conjecture in anabelian geometry [Reference KoenigsmannKoe05].
In positive characteristic, there is no comparable characterisation of local fields. Efrat and Fesenko in [Reference Efrat and FesenkoEF99] analyse the structure of fields whose absolute Galois group is isomorphic (as a profinite group) to the absolute Galois group of a local field
![]() $\mathbb{F}_q(\!(t)\!)$
. The characterisation of such fields was previously posed as [Reference EfratEfr95, Problem 4.6]. Such fields always carry a non-trivial henselian valuation, yet Efrat and Fesenko show, by examples, that a wide variety of fields occurs: this includes examples of characteristic 0, examples of arbitrarily large imperfection degree, and examples with imperfect residue field.
$\mathbb{F}_q(\!(t)\!)$
. The characterisation of such fields was previously posed as [Reference EfratEfr95, Problem 4.6]. Such fields always carry a non-trivial henselian valuation, yet Efrat and Fesenko show, by examples, that a wide variety of fields occurs: this includes examples of characteristic 0, examples of arbitrarily large imperfection degree, and examples with imperfect residue field.
In the present article we show that, once information concerning the Brauer group of K, or rather its p-torsion subgroup, is added to the Galois-theoretic data, the pathologies of [Reference Efrat and FesenkoEF99] disappear, and in fact a characterisation of local fields
![]() $\mathbb{F}_q(\!(t)\!)$
up to isomorphism is obtained, which is a characterisation much stronger than in the p-adic setting (where p-adic local fields cannot be distinguished Galois-theoretically from the larger class of p-adically closed fields).
$\mathbb{F}_q(\!(t)\!)$
up to isomorphism is obtained, which is a characterisation much stronger than in the p-adic setting (where p-adic local fields cannot be distinguished Galois-theoretically from the larger class of p-adically closed fields).
Theorem 1.1. Let p be a prime number,
![]() $q = p^n$
for some
$q = p^n$
for some
![]() $n \geq 1$
. Let K be a field satisfying the following axioms:
$n \geq 1$
. Let K be a field satisfying the following axioms:
-
(Gal) the absolute Galois group
 $\text{G}_K = \text{Gal}(K^{\mathrm{sep}}/K)$
is isomorphic to
$\text{G}_K = \text{Gal}(K^{\mathrm{sep}}/K)$
is isomorphic to
 $\text{G}_{\mathbb{F}_q(\!(t)\!)}$
;
$\text{G}_{\mathbb{F}_q(\!(t)\!)}$
; -
(Imp) K has exponent of imperfection at most 1;
-
(Brau) the p-torsion part
 $\text{Br}(K)[p]$
of the Brauer group of K is isomorphic to
$\text{Br}(K)[p]$
of the Brauer group of K is isomorphic to
 $\mathbb{Z}/p$
; and
$\mathbb{Z}/p$
; and -
(Pair) the natural pairing
 $\text{Hom}(\text{G}_K, \mathbb{Z}/p) \times K^\times/K^{\times p} \to \text{Br}(K)[p]$
(see § 2) induces an isomorphism
$\text{Hom}(\text{G}_K, \mathbb{Z}/p) \times K^\times/K^{\times p} \to \text{Br}(K)[p]$
(see § 2) induces an isomorphism
 $K^\times/K^{\times p} \cong \text{Hom}(\text{Hom}(\text{G}_K, \mathbb{Z}/p), \text{Br}(K)[p])$
.
$K^\times/K^{\times p} \cong \text{Hom}(\text{Hom}(\text{G}_K, \mathbb{Z}/p), \text{Br}(K)[p])$
.
Then K is isomorphic to the local field
![]() $\mathbb{F}_q(\!(t)\!)$
.
$\mathbb{F}_q(\!(t)\!)$
.
It is a consequence of local class field theory that, conversely, the local field
![]() $\mathbb{F}_q(\!(t)\!)$
satisfies the given axioms; see Proposition 2.2. We also give a strengthened version of Theorem 1.1 requiring an isomorphism not of full absolute Galois groups, but only of certain quotients; see Theorem 5.7. This is in the spirit of further developments of the anabelian and valuation-theoretic results mentioned above; see [Reference PopPop17, Reference TopazTop17, Reference Efrat and MináčEM12] for samples of a much wider literature.
$\mathbb{F}_q(\!(t)\!)$
satisfies the given axioms; see Proposition 2.2. We also give a strengthened version of Theorem 1.1 requiring an isomorphism not of full absolute Galois groups, but only of certain quotients; see Theorem 5.7. This is in the spirit of further developments of the anabelian and valuation-theoretic results mentioned above; see [Reference PopPop17, Reference TopazTop17, Reference Efrat and MináčEM12] for samples of a much wider literature.
We are not concerned here with reconstructing the local field
![]() $\mathbb{F}_q(\!(t)\!)$
functorially from its absolute Galois group, in the sense of identifying the group of field automorphisms with the outer automorphism group of the absolute Galois group. This was already done in [Reference AbrashkinAbr10] (following [Reference MochizukiMoc97] in the p-adic case), after endowing the absolute Galois group with the ramification filtration.
$\mathbb{F}_q(\!(t)\!)$
functorially from its absolute Galois group, in the sense of identifying the group of field automorphisms with the outer automorphism group of the absolute Galois group. This was already done in [Reference AbrashkinAbr10] (following [Reference MochizukiMoc97] in the p-adic case), after endowing the absolute Galois group with the ramification filtration.
Let us comment on why the axioms considered in Theorem 1.1 are natural. In characteristic
![]() $p > 0$
, absolute Galois groups fail to give much information ‘at the prime p’; this is most plainly visible in Galois cohomology, since the p-Sylow subgroups of such absolute Galois groups are projective [Reference Neukirch, Schmidt and WingbergNSW08, Corollary 6.1.3]. There is an alternative definition of cohomology groups
$p > 0$
, absolute Galois groups fail to give much information ‘at the prime p’; this is most plainly visible in Galois cohomology, since the p-Sylow subgroups of such absolute Galois groups are projective [Reference Neukirch, Schmidt and WingbergNSW08, Corollary 6.1.3]. There is an alternative definition of cohomology groups
![]() $H^i(K,\mathbb{Z}/p(j))$
, which in characteristic away from p we take as a synonym for the Galois cohomology
$H^i(K,\mathbb{Z}/p(j))$
, which in characteristic away from p we take as a synonym for the Galois cohomology
![]() $H^i(\text{G}_K, \mu_p^{\otimes j})$
, which remedies this defect; see [Reference KatoKat86, p.143]. For instance, with this definition we have
$H^i(\text{G}_K, \mu_p^{\otimes j})$
, which remedies this defect; see [Reference KatoKat86, p.143]. For instance, with this definition we have
![]() $H^2(K, \mathbb{Z}/p(1)) = \text{Br}(K)[p]$
and
$H^2(K, \mathbb{Z}/p(1)) = \text{Br}(K)[p]$
and
![]() $H^1(K, \mathbb{Z}/p(1)) = K^\times/p$
for all fields K, whether of characteristic p or not. With this notation, Theorem 1.1 can be rewritten more suggestively in the following way.
$H^1(K, \mathbb{Z}/p(1)) = K^\times/p$
for all fields K, whether of characteristic p or not. With this notation, Theorem 1.1 can be rewritten more suggestively in the following way.
Theorem 1.2. Let p be a prime number,
![]() $q = p^n$
for some
$q = p^n$
for some
![]() $n \geq 1$
. Let K be a field satisfying the following axioms:
$n \geq 1$
. Let K be a field satisfying the following axioms:
-
(Gal)
 $\text{G}_K \cong \text{G}_{\mathbb{F}_q(\!(t)\!)}$
;
$\text{G}_K \cong \text{G}_{\mathbb{F}_q(\!(t)\!)}$
; -
(Impʹ)
 $H^2(K, \mathbb{Z}/p(2)) = 0$
;
$H^2(K, \mathbb{Z}/p(2)) = 0$
; -
(Brauʹ)
 $H^2(K, \mathbb{Z}/p(1)) \cong \mathbb{Z}/p\mathbb{Z}$
; and
$H^2(K, \mathbb{Z}/p(1)) \cong \mathbb{Z}/p\mathbb{Z}$
; and -
(Pairʹ) The cup-product pairing
 $H^1(K, \mathbb{Z}/p(0)) \times H^1(K, \mathbb{Z}/p(1)) \to H^2(K, \mathbb{Z}/p(1))$
induces an isomorphism
$H^1(K, \mathbb{Z}/p(0)) \times H^1(K, \mathbb{Z}/p(1)) \to H^2(K, \mathbb{Z}/p(1))$
induces an isomorphism
 $H^1(K, \mathbb{Z}/p(1)) \cong \text{Hom}(H^1(K, \mathbb{Z}/p(0)), H^2(K, \mathbb{Z}/p(1)))$
.
$H^1(K, \mathbb{Z}/p(1)) \cong \text{Hom}(H^1(K, \mathbb{Z}/p(0)), H^2(K, \mathbb{Z}/p(1)))$
.
Then K is isomorphic to the local field
![]() $\mathbb{F}_q(\!(t)\!)$
.
$\mathbb{F}_q(\!(t)\!)$
.
This suggests that the additional axioms beyond
![]() $\text{G}_K \cong \text{G}_{\mathbb{F}_q(\!(t)\!)}$
merely serve to fix the defect concerning information at p of Galois cohomology in characteristic p.
$\text{G}_K \cong \text{G}_{\mathbb{F}_q(\!(t)\!)}$
merely serve to fix the defect concerning information at p of Galois cohomology in characteristic p.
The definition of cohomology groups
![]() $H^i(K, \mathbb{Z}/p(i))$
involves Milnor K-groups modulo p; in particular, a further phrasing of the axioms asserts that the mod p graded Milnor K-ring
$H^i(K, \mathbb{Z}/p(i))$
involves Milnor K-groups modulo p; in particular, a further phrasing of the axioms asserts that the mod p graded Milnor K-ring
![]() $\operatorname{K}^M_{\ast}(K^{\mathrm{sep}})/p$
of the separable closure of K together with its
$\operatorname{K}^M_{\ast}(K^{\mathrm{sep}})/p$
of the separable closure of K together with its
![]() $\text{G}_K$
-action is isomorphic to the corresponding data for
$\text{G}_K$
-action is isomorphic to the corresponding data for
![]() $\mathbb{F}_q(\!(t)\!)$
. In this sense, our theorem is reminiscent of Topaz’s work on the characterisation of fields up to isomorphism by their Milnor K-ring [Reference TopazTop22]. However, our axioms are much closer to being purely Galois-theoretic since we only consider mod p data.
$\mathbb{F}_q(\!(t)\!)$
. In this sense, our theorem is reminiscent of Topaz’s work on the characterisation of fields up to isomorphism by their Milnor K-ring [Reference TopazTop22]. However, our axioms are much closer to being purely Galois-theoretic since we only consider mod p data.
The proof of Theorem 1.1 is in two steps. Firstly, we use Galois-theoretic information at primes
![]() $l \neq p$
to show that K carries a non-trivial henselian valuation v. This is standard and can be found in [Reference Efrat and FesenkoEF99]. We recapitulate these results in § 3, where we also correct a mistake in [Reference Efrat and FesenkoEF99]. Secondly, we use the additional information given by the Brauer group to show that the valuation v is discrete with finite residue field, and K is complete. This is done in § 4, and is loosely inspired by Pop’s use of pro-p information in the absolute Galois group
$l \neq p$
to show that K carries a non-trivial henselian valuation v. This is standard and can be found in [Reference Efrat and FesenkoEF99]. We recapitulate these results in § 3, where we also correct a mistake in [Reference Efrat and FesenkoEF99]. Secondly, we use the additional information given by the Brauer group to show that the valuation v is discrete with finite residue field, and K is complete. This is done in § 4, and is loosely inspired by Pop’s use of pro-p information in the absolute Galois group
![]() $\text{G}_{\mathbb{Q}_p}$
in [Reference PopPop88, Theorem E.9].
$\text{G}_{\mathbb{Q}_p}$
in [Reference PopPop88, Theorem E.9].
The phenomenon found here, that information away from the residue characteristic p, when compared with information at the prime p, is much easier to use with the generally available tools but also yields much weaker results, seems quite typical. See also [Reference Koenigsmann and StrømmenKS24] in this regard.
2. Discussion of the axioms
Let K be an arbitrary field and p a prime number. We briefly recall some basic properties of the Brauer group, and define the pairing function
occurring in our axioms. Here and throughout we write
![]() $\text{Hom}(\text{G}_K, \mathbb{Z}/p)$
for the (discrete) abelian group of continuous group homomorphisms from
$\text{Hom}(\text{G}_K, \mathbb{Z}/p)$
for the (discrete) abelian group of continuous group homomorphisms from
![]() $\text{G}_K$
to the discrete group
$\text{G}_K$
to the discrete group
![]() $\mathbb{Z}/p$
, we write
$\mathbb{Z}/p$
, we write
![]() $K^\times/p$
for the group
$K^\times/p$
for the group
![]() $K^\times/K^{\times p}$
of pth power classes, and we write
$K^\times/K^{\times p}$
of pth power classes, and we write
![]() $\text{Br}(K)[p]$
for the set of elements of
$\text{Br}(K)[p]$
for the set of elements of
![]() $\text{Br}(K)$
of order dividing p.
$\text{Br}(K)$
of order dividing p.
The Brauer group
![]() $\text{Br}(K)$
of K can equivalently be defined as the Galois cohomology group
$\text{Br}(K)$
of K can equivalently be defined as the Galois cohomology group
![]() $H^2(\text{G}_K, {K^{\mathrm{sep}}}^\times)$
, or as the collection of central simple algebras over K modulo Brauer equivalence with the tensor product as a binary operation. We will not need this second viewpoint, which is explored in, for instance, [Reference Gille and SzamuelyGS17, § 2.4]; see [Reference Gille and SzamuelyGS17, Theorem 4.4.3] for the equivalence of the definitions.
$H^2(\text{G}_K, {K^{\mathrm{sep}}}^\times)$
, or as the collection of central simple algebras over K modulo Brauer equivalence with the tensor product as a binary operation. We will not need this second viewpoint, which is explored in, for instance, [Reference Gille and SzamuelyGS17, § 2.4]; see [Reference Gille and SzamuelyGS17, Theorem 4.4.3] for the equivalence of the definitions.
Given a character
![]() $\chi \colon \text{G}_K \to \mathbb{Z}/p$
and an element
$\chi \colon \text{G}_K \to \mathbb{Z}/p$
and an element
![]() $a \in K^\times$
, we can define an element
$a \in K^\times$
, we can define an element
![]() $(\chi, a) \in \text{Br}(K)$
as follows (see [Reference SerreSer68, Chapitre XIV, § 1] or [Reference Gille and SzamuelyGS17, Proposition 4.7.3]). Observe that
$(\chi, a) \in \text{Br}(K)$
as follows (see [Reference SerreSer68, Chapitre XIV, § 1] or [Reference Gille and SzamuelyGS17, Proposition 4.7.3]). Observe that
![]() $\chi \in \text{Hom}(\text{G}_K, \mathbb{Z}/p) = H^1(\text{G}_K, \mathbb{Z}/p)$
, and we have an exact sequence
$\chi \in \text{Hom}(\text{G}_K, \mathbb{Z}/p) = H^1(\text{G}_K, \mathbb{Z}/p)$
, and we have an exact sequence
![]() $0 \to \mathbb{Z} \to \mathbb{Z} \to \mathbb{Z}/p \to 0$
of abelian groups with trivial
$0 \to \mathbb{Z} \to \mathbb{Z} \to \mathbb{Z}/p \to 0$
of abelian groups with trivial
![]() $\text{G}_K$
-action, where the first map is multiplication by p. Hence we can apply the associated boundary map
$\text{G}_K$
-action, where the first map is multiplication by p. Hence we can apply the associated boundary map
![]() $\delta$
in cohomology to obtain an element
$\delta$
in cohomology to obtain an element
![]() $\delta(\chi) \in H^2(\text{G}_K, \mathbb{Z})$
. Secondly, we have
$\delta(\chi) \in H^2(\text{G}_K, \mathbb{Z})$
. Secondly, we have
![]() $a \in K^\times = H^0(\text{G}_K, {K^{\mathrm{sep}}}^\times)$
. Taking the cup product of these two cohomology classes we obtain
$a \in K^\times = H^0(\text{G}_K, {K^{\mathrm{sep}}}^\times)$
. Taking the cup product of these two cohomology classes we obtain
![]() $(\chi, a) := \delta(\chi) \cup a \in H^2(\text{G}_K, {K^{\mathrm{sep}}}^\times) = \text{Br}(K)$
. From the central simple algebra viewpoint,
$(\chi, a) := \delta(\chi) \cup a \in H^2(\text{G}_K, {K^{\mathrm{sep}}}^\times) = \text{Br}(K)$
. From the central simple algebra viewpoint,
![]() $(\chi, a)$
is the class of the cyclic algebra associated to
$(\chi, a)$
is the class of the cyclic algebra associated to
![]() $\chi$
and a. By construction, this gives a bilinear map of abelian groups
$\chi$
and a. By construction, this gives a bilinear map of abelian groups
![]() $\text{Hom}(\text{G}_K, \mathbb{Z}/p) \times K^\times \to \text{Br}(K)$
. Since
$\text{Hom}(\text{G}_K, \mathbb{Z}/p) \times K^\times \to \text{Br}(K)$
. Since
![]() $\text{Hom}(\text{G}_K, \mathbb{Z}/p)$
is a p-torsion group, it follows that the image must actually lie in
$\text{Hom}(\text{G}_K, \mathbb{Z}/p)$
is a p-torsion group, it follows that the image must actually lie in
![]() $\text{Br}(K)[p]$
, and the second argument factors through
$\text{Br}(K)[p]$
, and the second argument factors through
![]() $K^\times/p$
. Thus we have the desired bilinear pairing
$K^\times/p$
. Thus we have the desired bilinear pairing
![]() $\text{Hom}(\text{G}_K, \mathbb{Z}/p) \times K^\times/p \to \text{Br}(K)[p]$
. This pairing induces a group homomorphism
$\text{Hom}(\text{G}_K, \mathbb{Z}/p) \times K^\times/p \to \text{Br}(K)[p]$
. This pairing induces a group homomorphism
where the right-hand side is the group of homomorphisms
![]() $\text{Hom}(\text{G}_K, \mathbb{Z}/p) \to \text{Br}(K)[p]$
of discrete groups.
$\text{Hom}(\text{G}_K, \mathbb{Z}/p) \to \text{Br}(K)[p]$
of discrete groups.
An essential property of the pairing
![]() $(\cdot, \cdot)$
is given in the following lemma.
$(\cdot, \cdot)$
is given in the following lemma.
Lemma 2.1. Let
![]() $a \in K^\times$
and let
$a \in K^\times$
and let
![]() $\chi \colon \text{G}_K \to \mathbb{Z}/p$
be a non-zero homomorphism. Let
$\chi \colon \text{G}_K \to \mathbb{Z}/p$
be a non-zero homomorphism. Let
![]() $L/K$
be the
$L/K$
be the
![]() $\mathbb{Z}/p$
-extension associated to the index-p normal subgroup
$\mathbb{Z}/p$
-extension associated to the index-p normal subgroup
![]() $\ker(\chi)$
of
$\ker(\chi)$
of
![]() $\text{G}_K$
. Then
$\text{G}_K$
. Then
![]() $(\chi, a) = 0$
in
$(\chi, a) = 0$
in
![]() $\text{Br}(K)[p]$
if and only if a is a norm of the field extension
$\text{Br}(K)[p]$
if and only if a is a norm of the field extension
![]() $L/K$
.
$L/K$
.
Proof. See [Reference Gille and SzamuelyGS17, Corollary 4.7.5].
Let us show that local fields
![]() $\mathbb{F}_q(\!(t)\!)$
satisfy the axioms of Theorem 1.1.
$\mathbb{F}_q(\!(t)\!)$
satisfy the axioms of Theorem 1.1.
Proposition 2.2. Suppose K is a non-archimedean local field of arbitrary characteristic; for instance,
![]() $K = \mathbb{F}_q(\!(t)\!)$
for some prime power q (not necessarily a power of p). Then
$K = \mathbb{F}_q(\!(t)\!)$
for some prime power q (not necessarily a power of p). Then
![]() $\text{Br}(K)[p] \cong \mathbb{Z}/p$
, and the pairing above induces an isomorphism
$\text{Br}(K)[p] \cong \mathbb{Z}/p$
, and the pairing above induces an isomorphism
Proof. This is a consequence of local class field theory. Firstly, there is a canonical isomorphism
![]() $\operatorname{inv}_K \colon \text{Br}(K) \xrightarrow{\sim} \mathbb{Q}/\mathbb{Z}$
, and thus
$\operatorname{inv}_K \colon \text{Br}(K) \xrightarrow{\sim} \mathbb{Q}/\mathbb{Z}$
, and thus
![]() $\text{Br}(K)[p] \cong \frac{1}{p}\mathbb{Z}/\mathbb{Z} \cong \mathbb{Z}/p$
[Reference Neukirch, Schmidt and WingbergNSW08, Corollary 7.1.6].
$\text{Br}(K)[p] \cong \frac{1}{p}\mathbb{Z}/\mathbb{Z} \cong \mathbb{Z}/p$
[Reference Neukirch, Schmidt and WingbergNSW08, Corollary 7.1.6].
Secondly, class field theory provides the reciprocity homomorphism
which fits into the following exact sequence of abelian groups [Reference Neukirch, Schmidt and WingbergNSW08, Theorem 7.2.11] (cf. also [Reference SerreSer68, Chapitre XIII, § 4, Remarque after Proposition 13]):
Since the group
![]() $\hat{\mathbb{Z}}/\mathbb{Z}$
is torsion-free and divisible, a simple diagram chase shows that the induced homomorphism
$\hat{\mathbb{Z}}/\mathbb{Z}$
is torsion-free and divisible, a simple diagram chase shows that the induced homomorphism
![]() $K^\times/p \to \text{G}_K^{\mathrm{ab}}/p$
is an isomorphism. (Alternatively, take the tensor product of the sequence above with the abelian group
$K^\times/p \to \text{G}_K^{\mathrm{ab}}/p$
is an isomorphism. (Alternatively, take the tensor product of the sequence above with the abelian group
![]() $\mathbb{Z}/p$
, and use the fact that
$\mathbb{Z}/p$
, and use the fact that
![]() $\operatorname{Tor}^\mathbb{Z}_1(\hat{\mathbb{Z}}/\mathbb{Z}, \mathbb{Z}/p)$
and
$\operatorname{Tor}^\mathbb{Z}_1(\hat{\mathbb{Z}}/\mathbb{Z}, \mathbb{Z}/p)$
and
![]() $(\hat{\mathbb{Z}}/\mathbb{Z})/p$
both vanish, again since
$(\hat{\mathbb{Z}}/\mathbb{Z})/p$
both vanish, again since
![]() $\hat{\mathbb{Z}}/\mathbb{Z}$
is torsion-free and divisible.) By Pontryagin duality, we further have a canonical isomorphism
$\hat{\mathbb{Z}}/\mathbb{Z}$
is torsion-free and divisible.) By Pontryagin duality, we further have a canonical isomorphism
![]() $\text{G}_K^{\mathrm{ab}}/p \cong \text{Hom}(\text{Hom}(\text{G}_K^{\mathrm{ab}}/p, \mathbb{Z}/p), \mathbb{Z}/p) = \text{Hom}(\text{Hom}(G_K, \mathbb{Z}/p), \mathbb{Z}/p)$
.
$\text{G}_K^{\mathrm{ab}}/p \cong \text{Hom}(\text{Hom}(\text{G}_K^{\mathrm{ab}}/p, \mathbb{Z}/p), \mathbb{Z}/p) = \text{Hom}(\text{Hom}(G_K, \mathbb{Z}/p), \mathbb{Z}/p)$
.
We obtain a diagram

where the arrow on the left is induced by the pairing, the arrow at the top is induced by the reciprocity map and Pontryagin duality, and the diagonal arrow is induced by the canonical isomorphism
![]() $\operatorname{inv}_K$
. The diagram commutes; see [Reference SerreSer68, Chapitre XIV, § 1, Proposition 3] or [Reference Neukirch, Schmidt and WingbergNSW08, Proposition 7.2.12]. Since the top and the diagonal arrows are isomorphisms, the same must be true for the arrow on the left.
$\operatorname{inv}_K$
. The diagram commutes; see [Reference SerreSer68, Chapitre XIV, § 1, Proposition 3] or [Reference Neukirch, Schmidt and WingbergNSW08, Proposition 7.2.12]. Since the top and the diagonal arrows are isomorphisms, the same must be true for the arrow on the left.
A basic observation concerning fields satisfying the axioms of Theorem 1.1 is the following.
Lemma 2.3. Suppose K satisfies
![]() $\text{Br}(K)[p] \neq 0$
and
$\text{Br}(K)[p] \neq 0$
and
![]() $\text{G}_K$
has p-cohomological dimension at most 1. Then K has characteristic p.
$\text{G}_K$
has p-cohomological dimension at most 1. Then K has characteristic p.
Proof. If K did not have characteristic p, we would have
![]() $\text{Br}(K)[p] = H^2(\text{G}_K, \mu_p)$
[Reference Gille and SzamuelyGS17, Corollary 4.4.5], but the left-hand side is non-zero, and
$\text{Br}(K)[p] = H^2(\text{G}_K, \mu_p)$
[Reference Gille and SzamuelyGS17, Corollary 4.4.5], but the left-hand side is non-zero, and
![]() $\text{G}_K$
has p-cohomological dimension at most 1.
$\text{G}_K$
has p-cohomological dimension at most 1.
The hypothesis on p-cohomological dimension is satisfied by the absolute Galois group
![]() $\text{G}_{\mathbb{F}_q(\!(t)\!)}$
, as indeed it is by the absolute Galois group of any field of characteristic p [Reference Neukirch, Schmidt and WingbergNSW08, Corollary 6.1.3]. We later give a strengthened version of Lemma 2.3, only requiring Galois-theoretic information on a certain quotient of
$\text{G}_{\mathbb{F}_q(\!(t)\!)}$
, as indeed it is by the absolute Galois group of any field of characteristic p [Reference Neukirch, Schmidt and WingbergNSW08, Corollary 6.1.3]. We later give a strengthened version of Lemma 2.3, only requiring Galois-theoretic information on a certain quotient of
![]() $\text{G}_K$
. Since this is more complicated to prove, and is not needed for Theorem 1.1, we defer it to Lemma 5.1.
$\text{G}_K$
. Since this is more complicated to prove, and is not needed for Theorem 1.1, we defer it to Lemma 5.1.
Let us now discuss the rephrasing of Theorem 1.1 as Theorem 1.2, using Kato’s cohomology groups
![]() $H^i(K, \mathbb{Z}/p(j))$
. For K of characteristic not p, these groups are defined as Galois cohomology groups
$H^i(K, \mathbb{Z}/p(j))$
. For K of characteristic not p, these groups are defined as Galois cohomology groups
![]() $H^i(\text{G}_K, \mu_p^{\otimes j})$
and, in particular,
$H^i(\text{G}_K, \mu_p^{\otimes j})$
and, in particular,
![]() $H^2(K, \mathbb{Z}/p(1)) \cong \text{Br}(K)[p]$
[Reference KatoKat86, p.143]. By Lemma 2.3, we may therefore assume for the purposes of comparing the axioms of Theorems 1.1 and 1.2 that K has characteristic p.
$H^2(K, \mathbb{Z}/p(1)) \cong \text{Br}(K)[p]$
[Reference KatoKat86, p.143]. By Lemma 2.3, we may therefore assume for the purposes of comparing the axioms of Theorems 1.1 and 1.2 that K has characteristic p.
We may then take it as the definition of these groups that
![]() $H^i(K, \mathbb{Z}/p(i)) = \operatorname{K}^M_i(K)/p$
and
$H^i(K, \mathbb{Z}/p(i)) = \operatorname{K}^M_i(K)/p$
and
![]() $H^{i+1}(K, \mathbb{Z}/p(i)) = H^1(\text{G}_K, \operatorname{K}^M_i(K^{\mathrm{sep}})/p)$
, where the last group is a Galois cohomology group, and
$H^{i+1}(K, \mathbb{Z}/p(i)) = H^1(\text{G}_K, \operatorname{K}^M_i(K^{\mathrm{sep}})/p)$
, where the last group is a Galois cohomology group, and
![]() $\operatorname{K}^M_\ast$
denotes the graded Milnor K-ring. (See [Reference MerkurjevMer03, Appendix A, p.152] and the Bloch–Kato–Gabber Theorem, cf. [Reference KatoKat86, p.149, (1.2.1)].)
$\operatorname{K}^M_\ast$
denotes the graded Milnor K-ring. (See [Reference MerkurjevMer03, Appendix A, p.152] and the Bloch–Kato–Gabber Theorem, cf. [Reference KatoKat86, p.149, (1.2.1)].)
This means we have
![]() $H^1(K, \mathbb{Z}/p(1)) = \operatorname{K}^M_1(K)/p = K^\times/p$
,
$H^1(K, \mathbb{Z}/p(1)) = \operatorname{K}^M_1(K)/p = K^\times/p$
,
![]() $H^1(K, \mathbb{Z}/p(0)) = H^1(\text{G}_K, \mathbb{Z}/p) = \text{Hom}(\text{G}_K, \mathbb{Z}/p)$
, and
$H^1(K, \mathbb{Z}/p(0)) = H^1(\text{G}_K, \mathbb{Z}/p) = \text{Hom}(\text{G}_K, \mathbb{Z}/p)$
, and
![]() $H^2(K, \mathbb{Z}/p(1)) = H^1(\text{G}_K, {K^{\mathrm{sep}}}^\times/p) \cong \text{Br}(K)[p]$
(canonically) [Reference MerkurjevMer03, Appendix A, Example A.3(2)]. Since
$H^2(K, \mathbb{Z}/p(1)) = H^1(\text{G}_K, {K^{\mathrm{sep}}}^\times/p) \cong \text{Br}(K)[p]$
(canonically) [Reference MerkurjevMer03, Appendix A, Example A.3(2)]. Since
![]() $H^1(K, \mathbb{Z}/p(1)) = K^\times/p$
embeds into the Galois cohomology group
$H^1(K, \mathbb{Z}/p(1)) = K^\times/p$
embeds into the Galois cohomology group
![]() $H^0(\text{G}_K, {K^{\mathrm{sep}}}^\times/p)$
, the cup product in Galois cohomology yields a bilinear pairing
$H^0(\text{G}_K, {K^{\mathrm{sep}}}^\times/p)$
, the cup product in Galois cohomology yields a bilinear pairing
cf. [Reference MerkurjevMer03, Appendix A, (A.5)]. Standard facts (namely the compatibility of the cup product with the connecting homomorphisms in long exact sequences) show that this pairing agrees, up to sign, with the pairing into
![]() $\text{Br}(K)[p]$
defined above. This gives the equivalence of axioms (Pair) and (Pairʹ).
$\text{Br}(K)[p]$
defined above. This gives the equivalence of axioms (Pair) and (Pairʹ).
To establish the equivalence of Theorems 1.1 and 1.2, we also need to translate the axiom that
![]() $H^2(K, \mathbb{Z}/p(2)) = \operatorname{K}^M_2(K)/p$
vanishes into the statement that
$H^2(K, \mathbb{Z}/p(2)) = \operatorname{K}^M_2(K)/p$
vanishes into the statement that
![]() $[K : K^p] \leq p$
. Consider two elements
$[K : K^p] \leq p$
. Consider two elements
![]() $a, b \in K^\times$
. These are p-dependent, meaning that
$a, b \in K^\times$
. These are p-dependent, meaning that
![]() $[K^p(a,b) : K^p] \leq p$
if and only if the elements da and db of the vector space of absolute Kähler differentials
$[K^p(a,b) : K^p] \leq p$
if and only if the elements da and db of the vector space of absolute Kähler differentials
![]() $\Omega_K$
are linearly dependent, which is the case if and only if the differential form
$\Omega_K$
are linearly dependent, which is the case if and only if the differential form
![]() $da \wedge db \in \Omega^2_K$
vanishes; cf. [Reference Gille and SzamuelyGS17, Proposition A.8.11] or [Reference BourbakiBou07, Chapitre V, No 2, § 13, Théorème 1 a)]. By the Bloch–Kato–Gabber Theorem [Reference Gille and SzamuelyGS17, Theorem 9.5.2], the group
$da \wedge db \in \Omega^2_K$
vanishes; cf. [Reference Gille and SzamuelyGS17, Proposition A.8.11] or [Reference BourbakiBou07, Chapitre V, No 2, § 13, Théorème 1 a)]. By the Bloch–Kato–Gabber Theorem [Reference Gille and SzamuelyGS17, Theorem 9.5.2], the group
![]() $\operatorname{K}^M_2(K)/p$
naturally embeds into
$\operatorname{K}^M_2(K)/p$
naturally embeds into
![]() $\Omega^2_K$
, from which we deduce that
$\Omega^2_K$
, from which we deduce that
![]() $da \wedge db \in \Omega^2_K$
vanishes if and only if the symbol
$da \wedge db \in \Omega^2_K$
vanishes if and only if the symbol
![]() $\{ a, b \} \in \operatorname{K}^M_2(K)/p$
vanishes. This shows that the group
$\{ a, b \} \in \operatorname{K}^M_2(K)/p$
vanishes. This shows that the group
![]() $\operatorname{K}^M_2(K)/p$
vanishes if and only if any two
$\operatorname{K}^M_2(K)/p$
vanishes if and only if any two
![]() $a, b \in K^\times$
are p-dependent, i.e. if and only if
$a, b \in K^\times$
are p-dependent, i.e. if and only if
![]() $[K : K^p] \leq p$
.
$[K : K^p] \leq p$
.
3. Existence of a valuation
Let K be a field with
![]() $\text{G}_K \cong \text{G}_{\mathbb{F}_q(\!(t)\!)}$
. The goal of this section is to show that K carries a non-trivial henselian valuation v whose residue field Kv is not p-closed, i.e. such that Kv has a
$\text{G}_K \cong \text{G}_{\mathbb{F}_q(\!(t)\!)}$
. The goal of this section is to show that K carries a non-trivial henselian valuation v whose residue field Kv is not p-closed, i.e. such that Kv has a
![]() $\mathbb{Z}/p$
-extension, or equivalently the maximal pro-p quotient
$\mathbb{Z}/p$
-extension, or equivalently the maximal pro-p quotient
![]() $\text{G}_{Kv}(p)$
is not trivial.
$\text{G}_{Kv}(p)$
is not trivial.
Remark 3.1. This result follows in principle from [Reference Efrat and FesenkoEF99, Proposition 4.3(d)]. However, the proof of this proposition relies on [Reference Efrat and FesenkoEF99, Lemma 4.2], a lemma concerning profinite groups, which is false. The lemma claims, in particular, that for a profinite group H such that the l-Sylow subgroups of H are isomorphic to
![]() $\mathbb{Z}_l$
for every prime number l, the maximal prime-to-p quotient H(p’) is isomorphic to
$\mathbb{Z}_l$
for every prime number l, the maximal prime-to-p quotient H(p’) is isomorphic to
![]() $\hat{\mathbb{Z}}/\mathbb{Z}_p$
for every p.
$\hat{\mathbb{Z}}/\mathbb{Z}_p$
for every p.
To see that this is false, consider the profinite group
![]() $H = \mathbb{Z}_2 \ltimes \prod_{l \neq 2} \mathbb{Z}_l$
, where the product is over odd primes l, and
$H = \mathbb{Z}_2 \ltimes \prod_{l \neq 2} \mathbb{Z}_l$
, where the product is over odd primes l, and
![]() $x \in \mathbb{Z}_2$
acts on
$x \in \mathbb{Z}_2$
acts on
![]() $\prod_{l \neq 2} \mathbb{Z}_l$
as multiplication by
$\prod_{l \neq 2} \mathbb{Z}_l$
as multiplication by
![]() $(-1)^x$
. Then every Sylow subgroup of H is procyclic. However, for
$(-1)^x$
. Then every Sylow subgroup of H is procyclic. However, for
![]() $p \neq 2$
, the maximal prime-to-p quotient H(p’) is the non-abelian
$p \neq 2$
, the maximal prime-to-p quotient H(p’) is the non-abelian
![]() $\mathbb{Z}_2 \ltimes \prod_{l \neq 2, p} \mathbb{Z}_l$
, which contradicts [Reference Efrat and FesenkoEF99, Lemma 4.2]. One can also check that the maximal prime-to-2 quotient H(2’) is the trivial group, for a further contradiction. The mistake in the proof of [Reference Efrat and FesenkoEF99, Lemma 4.2] lies in an erroneous statement concerning the canonical projection
$\mathbb{Z}_2 \ltimes \prod_{l \neq 2, p} \mathbb{Z}_l$
, which contradicts [Reference Efrat and FesenkoEF99, Lemma 4.2]. One can also check that the maximal prime-to-2 quotient H(2’) is the trivial group, for a further contradiction. The mistake in the proof of [Reference Efrat and FesenkoEF99, Lemma 4.2] lies in an erroneous statement concerning the canonical projection
![]() $\hat{F} \to \hat{F}(\mathrm{ab}, p')$
in the notation there, where
$\hat{F} \to \hat{F}(\mathrm{ab}, p')$
in the notation there, where
![]() $\hat{F}$
is a free profinite group.
$\hat{F}$
is a free profinite group.
Although parts of the proof of [Reference Efrat and FesenkoEF99, Proposition 4.3] could be salvaged, we use this opportunity to give a new full proof of [Reference Efrat and FesenkoEF99, Proposition 4.3], or rather of a slightly strengthened formulation.
Proposition 3.2. There exists a non-trivial henselian valuation v on K such that Kv has characteristic p,
![]() $(vK : l\cdot vK) = l$
for every prime number
$(vK : l\cdot vK) = l$
for every prime number
![]() $l \neq p$
, the maximal prime-to-p quotient
$l \neq p$
, the maximal prime-to-p quotient
![]() $\text{G}_{Kv}(p')$
is isomorphic to
$\text{G}_{Kv}(p')$
is isomorphic to
![]() $\hat{\mathbb{Z}}/\mathbb{Z}_p$
, and
$\hat{\mathbb{Z}}/\mathbb{Z}_p$
, and
![]() $Kv \cap \overline{\mathbb{F}_p} \cong \mathbb{F}_q$
.
$Kv \cap \overline{\mathbb{F}_p} \cong \mathbb{F}_q$
.
Proof. The existence of a henselian valuation v with
![]() $(vK : l \cdot vK) = l$
for every
$(vK : l \cdot vK) = l$
for every
![]() $l \neq p$
and residue characteristic p is [Reference Efrat and FesenkoEF99, Theorem 4.1].
$l \neq p$
and residue characteristic p is [Reference Efrat and FesenkoEF99, Theorem 4.1].
(We mention in passing that this also follows very neatly from Koenigsmann’s characterisation of ‘tamely branching valuations’ as presented in [Reference Engler and PrestelEP05, Theorem 5.4.3]. Indeed, by the theorem the canonical henselian valuation v on K must be tamely branching at all
![]() $l \neq p$
since the same is true for
$l \neq p$
since the same is true for
![]() $\mathbb{F}_q(\!(t)\!)$
and this is a Galois-theoretic condition; the residue field Kv must have characteristic p by the argument of [Reference Efrat and FesenkoEF99, Theorem 4.1(b)]; and since the abelian normal subgroups of l-Sylow subgroups of
$\mathbb{F}_q(\!(t)\!)$
and this is a Galois-theoretic condition; the residue field Kv must have characteristic p by the argument of [Reference Efrat and FesenkoEF99, Theorem 4.1(b)]; and since the abelian normal subgroups of l-Sylow subgroups of
![]() $\text{G}_{\mathbb{F}_q(\!(t)\!)}$
are procyclic, it follows that
$\text{G}_{\mathbb{F}_q(\!(t)\!)}$
are procyclic, it follows that
![]() $[vK : l\cdot vK] = l$
from ramification theory.)
$[vK : l\cdot vK] = l$
from ramification theory.)
It remains to prove the assertions about
![]() $\text{G}_{Kv}(p')$
and
$\text{G}_{Kv}(p')$
and
![]() $Kv \cap \overline{\mathbb{F}_p}$
. We extensively use the theory of ramification and inertia subgroups as presented, for instance, in [Reference EfratEfr06, Chapter 15]. Let
$Kv \cap \overline{\mathbb{F}_p}$
. We extensively use the theory of ramification and inertia subgroups as presented, for instance, in [Reference EfratEfr06, Chapter 15]. Let
![]() $\sigma \colon \text{G}_{\mathbb{F}_q(\!(t)\!)} \to \text{G}_K$
be an isomorphism, and write T, V for the inertia and ramification subgroups of
$\sigma \colon \text{G}_{\mathbb{F}_q(\!(t)\!)} \to \text{G}_K$
be an isomorphism, and write T, V for the inertia and ramification subgroups of
![]() $\text{G}_{\mathbb{F}_q(\!(t)\!)}$
. Let
$\text{G}_{\mathbb{F}_q(\!(t)\!)}$
. Let
![]() $L/K$
be the fixed field of
$L/K$
be the fixed field of
![]() $\sigma(V) \leq \text{G}_K$
. Then
$\sigma(V) \leq \text{G}_K$
. Then
![]() $L/K$
is a Galois extension with Galois group isomorphic to
$L/K$
is a Galois extension with Galois group isomorphic to
![]() $\text{G}_{\mathbb{F}_q(\!(t)\!)}/V$
, so it is generated as a profinite group by two elements
$\text{G}_{\mathbb{F}_q(\!(t)\!)}/V$
, so it is generated as a profinite group by two elements
![]() $\sigma$
,
$\sigma$
,
![]() $\tau$
with the sole relation
$\tau$
with the sole relation
![]() $\sigma\tau\sigma^{-1} = \tau^q$
, i.e.
$\sigma\tau\sigma^{-1} = \tau^q$
, i.e.
![]() $\text{Gal}(L/K)$
is the semi-direct product of
$\text{Gal}(L/K)$
is the semi-direct product of
![]() $\langle\sigma\rangle \cong \hat{\mathbb{Z}}$
and
$\langle\sigma\rangle \cong \hat{\mathbb{Z}}$
and
![]() $\langle\tau\rangle \cong \hat{\mathbb{Z}}/\mathbb{Z}_p$
[Reference Neukirch, Schmidt and WingbergNSW08, Theorem 7.5.3]. Furthermore, the absolute Galois group of L is isomorphic to V, and is thus a free pro-p group. In particular, for every prime number
$\langle\tau\rangle \cong \hat{\mathbb{Z}}/\mathbb{Z}_p$
[Reference Neukirch, Schmidt and WingbergNSW08, Theorem 7.5.3]. Furthermore, the absolute Galois group of L is isomorphic to V, and is thus a free pro-p group. In particular, for every prime number
![]() $l \neq p$
the value group vL (where we also write v for the unique prolongation of the valuation v on K to L) is l-divisible.
$l \neq p$
the value group vL (where we also write v for the unique prolongation of the valuation v on K to L) is l-divisible.
The relative ramification subgroup R of
![]() $\text{Gal}(L/K)$
is a normal pro-p subgroup. The p-Sylow subgroups of
$\text{Gal}(L/K)$
is a normal pro-p subgroup. The p-Sylow subgroups of
![]() $\text{Gal}(L/K) = \langle \sigma, \tau\rangle$
are procyclic, so R is abelian. By [Reference Neukirch, Schmidt and WingbergNSW08, Corollary 7.5.7(ii)], R must be contained in
$\text{Gal}(L/K) = \langle \sigma, \tau\rangle$
are procyclic, so R is abelian. By [Reference Neukirch, Schmidt and WingbergNSW08, Corollary 7.5.7(ii)], R must be contained in
![]() $\langle\tau\rangle \cong \hat{\mathbb{Z}}/\mathbb{Z}_p$
, which has no pro-p part. Therefore R is trivial, i.e. the extension
$\langle\tau\rangle \cong \hat{\mathbb{Z}}/\mathbb{Z}_p$
, which has no pro-p part. Therefore R is trivial, i.e. the extension
![]() $L/K$
is tamely ramified.
$L/K$
is tamely ramified.
Thus the relative inertia group I of
![]() $L/K$
is an abelian normal subgroup of
$L/K$
is an abelian normal subgroup of
![]() $\text{Gal}(L/K) = \langle \sigma, \tau \rangle$
. By [Reference Neukirch, Schmidt and WingbergNSW08, Corollary 7.5.7(ii)] once more,
$\text{Gal}(L/K) = \langle \sigma, \tau \rangle$
. By [Reference Neukirch, Schmidt and WingbergNSW08, Corollary 7.5.7(ii)] once more,
![]() $I \leq \langle \tau\rangle \cong \hat{\mathbb{Z}} / \mathbb{Z}_p$
. We have the so-called ramification pairing
$I \leq \langle \tau\rangle \cong \hat{\mathbb{Z}} / \mathbb{Z}_p$
. We have the so-called ramification pairing
where
![]() $\mu(Lv)$
is the group of roots of unity in the residue field Lv (see [Reference EfratEfr06, Theorem 16.2.6]). (In the notation there, observe that L is the ramification subfield of
$\mu(Lv)$
is the group of roots of unity in the residue field Lv (see [Reference EfratEfr06, Theorem 16.2.6]). (In the notation there, observe that L is the ramification subfield of
![]() $L/K$
with respect to v since
$L/K$
with respect to v since
![]() $L/K$
is tamely ramified, and the value group vK agrees with the value group of the relative inertia field since
$L/K$
is tamely ramified, and the value group vK agrees with the value group of the relative inertia field since
![]() $L/K$
is separable, cf. the diagram on [Reference EfratEfr06, p.149].) The ramification pairing is bilinear with trivial left and right kernel, and it is continuous (where
$L/K$
is separable, cf. the diagram on [Reference EfratEfr06, p.149].) The ramification pairing is bilinear with trivial left and right kernel, and it is continuous (where
![]() $vL/vK$
and
$vL/vK$
and
![]() $\mu(Lv)$
carry the discrete topology and I its profinite topology). Since vL is l-divisible for every prime number
$\mu(Lv)$
carry the discrete topology and I its profinite topology). Since vL is l-divisible for every prime number
![]() $l \neq p$
, but vK is not, the torsion group
$l \neq p$
, but vK is not, the torsion group
![]() $vL/vK$
contains elements of arbitrary l-power order. The triviality of the right kernel of the pairing then implies that
$vL/vK$
contains elements of arbitrary l-power order. The triviality of the right kernel of the pairing then implies that
![]() $\mu(Lv)$
contains elements of arbitrary l-power order, and furthermore that the profinite group I must have non-trivial l-Sylow subgroup. It follows that Sylow subgroups of the quotient
$\mu(Lv)$
contains elements of arbitrary l-power order, and furthermore that the profinite group I must have non-trivial l-Sylow subgroup. It follows that Sylow subgroups of the quotient
![]() $\langle\tau\rangle/I$
are torsion, since the l-Sylow subgroup of both
$\langle\tau\rangle/I$
are torsion, since the l-Sylow subgroup of both
![]() $\langle\tau\rangle$
and I is isomorphic to
$\langle\tau\rangle$
and I is isomorphic to
![]() $\mathbb{Z}_l$
for every
$\mathbb{Z}_l$
for every
![]() $l \neq p$
.
$l \neq p$
.
We have
![]() $\text{Gal}(Lv/Kv) \cong \langle\sigma,\tau\rangle/I$
. In particular the p-Sylow subgroups of
$\text{Gal}(Lv/Kv) \cong \langle\sigma,\tau\rangle/I$
. In particular the p-Sylow subgroups of
![]() $\text{Gal}(Lv/Kv)$
are isomorphic to
$\text{Gal}(Lv/Kv)$
are isomorphic to
![]() $\mathbb{Z}_p$
, so
$\mathbb{Z}_p$
, so
![]() $\text{cd}_p \text{Gal}(Lv/Kv) = 1$
. Since
$\text{cd}_p \text{Gal}(Lv/Kv) = 1$
. Since
![]() $\text{G}_{Lv}$
is a pro-p group as a quotient of
$\text{G}_{Lv}$
is a pro-p group as a quotient of
![]() $\text{G}_L$
, it follows from [Reference Neukirch, Schmidt and WingbergNSW08, Theorem 3.5.6] that the exact sequence
$\text{G}_L$
, it follows from [Reference Neukirch, Schmidt and WingbergNSW08, Theorem 3.5.6] that the exact sequence
splits. Hence
![]() $\text{Gal}(Lv/Kv)$
is isomorphic to a subgroup of
$\text{Gal}(Lv/Kv)$
is isomorphic to a subgroup of
![]() $\text{G}_{Kv}$
and therefore torsion-free. Therefore the subgroup
$\text{G}_{Kv}$
and therefore torsion-free. Therefore the subgroup
![]() $\langle\tau\rangle/I$
of
$\langle\tau\rangle/I$
of
![]() $\langle\sigma,\tau\rangle/I \cong \text{Gal}(Lv/Kv)$
is also torsion-free. On the other hand, we have seen above that its Sylow subgroups are torsion, so we must have
$\langle\sigma,\tau\rangle/I \cong \text{Gal}(Lv/Kv)$
is also torsion-free. On the other hand, we have seen above that its Sylow subgroups are torsion, so we must have
![]() $I = \langle\tau\rangle$
. Thus
$I = \langle\tau\rangle$
. Thus
![]() $\text{Gal}(Lv/Kv) \cong \langle\sigma,\tau\rangle/I \cong \hat{\mathbb{Z}}$
. Since
$\text{Gal}(Lv/Kv) \cong \langle\sigma,\tau\rangle/I \cong \hat{\mathbb{Z}}$
. Since
![]() $\text{G}_{Lv}$
is pro-p, we deduce that
$\text{G}_{Lv}$
is pro-p, we deduce that
![]() $\text{G}_{Kv}(p') = \text{Gal}(Lv/Kv)(p') = \hat{\mathbb{Z}}/\mathbb{Z}_p$
.
$\text{G}_{Kv}(p') = \text{Gal}(Lv/Kv)(p') = \hat{\mathbb{Z}}/\mathbb{Z}_p$
.
It remains to prove that
![]() $Kv \cap \overline{\mathbb{F}_p} \cong \mathbb{F}_q$
. We saw above in our analysis of
$Kv \cap \overline{\mathbb{F}_p} \cong \mathbb{F}_q$
. We saw above in our analysis of
![]() $\mu(Lv)$
that Lv contains
$\mu(Lv)$
that Lv contains
![]() $l^s$
-roots of unity for every prime number
$l^s$
-roots of unity for every prime number
![]() $l \neq p$
and every
$l \neq p$
and every
![]() $s \geq 1$
. In other words, Lv contains the algebraic closure
$s \geq 1$
. In other words, Lv contains the algebraic closure
![]() $\overline{\mathbb{F}_p}$
.
$\overline{\mathbb{F}_p}$
.
The ramification pairing induces an isomorphism
![]() $I \cong \text{Hom}(vL/vK, \mu(Lv))$
[Reference EfratEfr06, Corollary 16.2.7(c)], where the homomorphism group is endowed with the topology of pointwise convergence. This isomorphism is compatible with the action of
$I \cong \text{Hom}(vL/vK, \mu(Lv))$
[Reference EfratEfr06, Corollary 16.2.7(c)], where the homomorphism group is endowed with the topology of pointwise convergence. This isomorphism is compatible with the action of
![]() $\langle\sigma\rangle \cong \text{Gal}(Lv/Kv)$
, where
$\langle\sigma\rangle \cong \text{Gal}(Lv/Kv)$
, where
![]() $\text{Gal}(Lv/Kv)$
acts on the homomorphism group via its action on
$\text{Gal}(Lv/Kv)$
acts on the homomorphism group via its action on
![]() $\mu(Lv)$
, and
$\mu(Lv)$
, and
![]() $\langle\sigma\rangle$
acts on I by conjugation.
$\langle\sigma\rangle$
acts on I by conjugation.
The automorphism group
![]() $\operatorname{Aut}(\overline{\mathbb{F}_p}) = \text{Gal}(\overline{\mathbb{F}_p}/\mathbb{F}_p)$
is isomorphic to
$\operatorname{Aut}(\overline{\mathbb{F}_p}) = \text{Gal}(\overline{\mathbb{F}_p}/\mathbb{F}_p)$
is isomorphic to
![]() $\hat{\mathbb{Z}}$
and is generated by the Frobenius automorphism
$\hat{\mathbb{Z}}$
and is generated by the Frobenius automorphism
![]() $x \mapsto x^p$
. Say the image of
$x \mapsto x^p$
. Say the image of
![]() $\sigma$
in
$\sigma$
in
![]() $\text{Gal}(Lv/Kv)$
acts on
$\text{Gal}(Lv/Kv)$
acts on
![]() $\overline{\mathbb{F}_p}$
as
$\overline{\mathbb{F}_p}$
as
![]() $x \mapsto x^{p^n}$
for some
$x \mapsto x^{p^n}$
for some
![]() $n \in \hat{\mathbb{Z}}$
. Therefore this element of
$n \in \hat{\mathbb{Z}}$
. Therefore this element of
![]() $\text{Gal}(Lv/Kv)$
acts on the abelian profinite group
$\text{Gal}(Lv/Kv)$
acts on the abelian profinite group
![]() $\text{Hom}(vL/vK, \mu(Lv))$
as multiplication by
$\text{Hom}(vL/vK, \mu(Lv))$
as multiplication by
![]() $p^n$
. Compatibility of the action with the isomorphism induced by the ramification pairing means that
$p^n$
. Compatibility of the action with the isomorphism induced by the ramification pairing means that
![]() $\sigma$
must act in the same way on I by conjugation. In other words, we have
$\sigma$
must act in the same way on I by conjugation. In other words, we have
![]() $\sigma\eta\sigma^{-1} = \eta^{p^n}$
for each
$\sigma\eta\sigma^{-1} = \eta^{p^n}$
for each
![]() $\eta \in I = \langle\tau\rangle$
. However, by construction of
$\eta \in I = \langle\tau\rangle$
. However, by construction of
![]() $\langle\sigma,\tau\rangle$
as a semi-direct product we know that
$\langle\sigma,\tau\rangle$
as a semi-direct product we know that
![]() $\sigma\eta\sigma^{-1} = \eta^q$
. This is only possible for all elements
$\sigma\eta\sigma^{-1} = \eta^q$
. This is only possible for all elements
![]() $\eta \in I = \langle\tau\rangle \cong \hat{\mathbb{Z}}/\mathbb{Z}_p$
if we have
$\eta \in I = \langle\tau\rangle \cong \hat{\mathbb{Z}}/\mathbb{Z}_p$
if we have
![]() $p^n = q$
as elements of
$p^n = q$
as elements of
![]() $(\hat{\mathbb{Z}}/\mathbb{Z}_p)^\times$
. It follows that an element
$(\hat{\mathbb{Z}}/\mathbb{Z}_p)^\times$
. It follows that an element
![]() $x \in \overline{\mathbb{F}_p}$
lies in Kv, i.e. is fixed by
$x \in \overline{\mathbb{F}_p}$
lies in Kv, i.e. is fixed by
![]() $\text{Gal}(Lv/Kv)$
, if and only if
$\text{Gal}(Lv/Kv)$
, if and only if
![]() $x^{p^n} = x^q = x$
. Therefore
$x^{p^n} = x^q = x$
. Therefore
![]() $\overline{\mathbb{F}_p} \cap Kv = \mathbb{F}_q$
.
$\overline{\mathbb{F}_p} \cap Kv = \mathbb{F}_q$
.
Proposition 3.2recovers [Reference Efrat and FesenkoEF99, Proposition 4.3], and also immediately implies the following desired corollary.
Corollary 3.3. There exists a non-trivial henselian valuation v on K such that the residue field Kv is not p-closed.
Proof. Let v be the valuation from Proposition 3.2. Since
![]() $\mathbb{F}_q$
has a
$\mathbb{F}_q$
has a
![]() $\mathbb{Z}/p$
-extension, so does Kv.
$\mathbb{Z}/p$
-extension, so does Kv.
We later give an alternative version of Corollary 3.3, requiring only weaker Galois-theoretic information, but also only yielding a p-henselian valuation. Since this is not needed for the basic result (Theorem 1.1), and the proof uses different techniques as it cannot rely on [Reference Efrat and FesenkoEF99, Theorem 4.1], we defer this to Proposition 5.3.
4. Consequences of the Brauer group axioms
Throughout this section, let K be a field such that:
-
(1) K has countably many
 $\mathbb{Z}/p$
-extensions;
$\mathbb{Z}/p$
-extensions; -
(2) K has characteristic p; and
-
(3) the axioms (Brau) and (Pair) from Theorem 1.1 are satisfied.
Artin–Schreier theory yields an isomorphism
![]() $\text{Hom}(\text{G}_K, \mathbb{Z}/p) \cong K/\wp(K)$
, where
$\text{Hom}(\text{G}_K, \mathbb{Z}/p) \cong K/\wp(K)$
, where
![]() $\wp(K)$
is the image of the group homomorphism
$\wp(K)$
is the image of the group homomorphism
![]() $\wp \colon K \to K, x \mapsto x^p - x$
[Reference Neukirch, Schmidt and WingbergNSW08, Corollary 6.1.2]. Our first assumption can therefore also be phrased as the assertion that the group
$\wp \colon K \to K, x \mapsto x^p - x$
[Reference Neukirch, Schmidt and WingbergNSW08, Corollary 6.1.2]. Our first assumption can therefore also be phrased as the assertion that the group
![]() $K/\wp(K)$
is countable. The Artin–Schreier isomorphism yields a pairing
$K/\wp(K)$
is countable. The Artin–Schreier isomorphism yields a pairing
![]() $[{\cdot}, {\cdot}) \colon K/\wp(K) \times K^\times/p \to \text{Br}(K)[p]$
from the pairing defined in § 2. (This notation is also used in [Reference SerreSer68, Chapitre XIV, § 5].) We will also consider
$[{\cdot}, {\cdot}) \colon K/\wp(K) \times K^\times/p \to \text{Br}(K)[p]$
from the pairing defined in § 2. (This notation is also used in [Reference SerreSer68, Chapitre XIV, § 5].) We will also consider
![]() $[{\cdot}, {\cdot})$
as a function defined on
$[{\cdot}, {\cdot})$
as a function defined on
![]() $K \times K^\times$
.
$K \times K^\times$
.
In this section we show that certain valuations v on K satisfy very strong properties. In the proof of Theorem 1.1, we will apply this to a valuation obtained (under the hypothesis (Gal), beyond the standing assumptions of this section introduced above) from the results of § 3. However, for the time being we develop the material for arbitrary valuations v, of which we will generally only assume that they are non-trivial, have non-p-closed residue field Kv, and are p-henselian. This last standard condition, see [Reference Chatzidakis and PereraCP17], means that the maximal ideal
![]() $\mathfrak{m}_v$
of the valuation ring is contained in
$\mathfrak{m}_v$
of the valuation ring is contained in
![]() $\wp(K)$
, or equivalently that the valuation extends uniquely to every
$\wp(K)$
, or equivalently that the valuation extends uniquely to every
![]() $\mathbb{Z}/p$
-extension of K. (We will meet the general condition of l-henselianity, where l is a prime not necessarily equal to the characteristic, in § 5 below.)
$\mathbb{Z}/p$
-extension of K. (We will meet the general condition of l-henselianity, where l is a prime not necessarily equal to the characteristic, in § 5 below.)
Lemma 4.1. For a p-henselian valuation v on K, we have
![]() $[{\mathcal{O}_v}, {1 + \mathfrak{m}_v}) = 0$
. More generally, for every
$[{\mathcal{O}_v}, {1 + \mathfrak{m}_v}) = 0$
. More generally, for every
![]() $0 \neq x \in \mathcal{O}_v$
, we have
$0 \neq x \in \mathcal{O}_v$
, we have
![]() $[{x^{-1}\mathcal{O}_v}, {1 + x\mathfrak{m}_v}) = 0$
.
$[{x^{-1}\mathcal{O}_v}, {1 + x\mathfrak{m}_v}) = 0$
.
Proof. Let
![]() $a \in x^{-1}\mathcal{O}_v$
, i.e.
$a \in x^{-1}\mathcal{O}_v$
, i.e.
![]() $v(a) \geq -v(x)$
, and consider the character
$v(a) \geq -v(x)$
, and consider the character
![]() $\chi \colon \text{G}_K \to \mathbb{Z}/p$
associated to
$\chi \colon \text{G}_K \to \mathbb{Z}/p$
associated to
![]() $a + \wp(K)$
. Let
$a + \wp(K)$
. Let
![]() $b \in 1 + x\mathfrak{m}_v$
. We must show that
$b \in 1 + x\mathfrak{m}_v$
. We must show that
![]() $(\chi, b) = 0$
. There is nothing to prove if
$(\chi, b) = 0$
. There is nothing to prove if
![]() $\chi = 0$
, so suppose otherwise. Let
$\chi = 0$
, so suppose otherwise. Let
![]() $L/K$
be the
$L/K$
be the
![]() $\mathbb{Z}/p$
-extension associated to
$\mathbb{Z}/p$
-extension associated to
![]() $\chi$
, which is precisely the extension of K generated by an element
$\chi$
, which is precisely the extension of K generated by an element
![]() $\alpha$
with
$\alpha$
with
![]() $\alpha^p - \alpha = a$
. By Lemma 2.1 we have to show that b is a norm of
$\alpha^p - \alpha = a$
. By Lemma 2.1 we have to show that b is a norm of
![]() $L/K$
. For an element
$L/K$
. For an element
![]() $y \in K$
, we have
$y \in K$
, we have
![]() $(\alpha+y)^p - (\alpha+y) - a - \wp(y) = 0$
, so
$(\alpha+y)^p - (\alpha+y) - a - \wp(y) = 0$
, so
![]() $X^p - X - a - \wp(y)$
is the minimal polynomial of
$X^p - X - a - \wp(y)$
is the minimal polynomial of
![]() $\alpha+y$
over K, and hence the norm of
$\alpha+y$
over K, and hence the norm of
![]() $\alpha+y$
is
$\alpha+y$
is
![]() $a + \wp(y)$
. The norm of
$a + \wp(y)$
. The norm of
![]() $({\alpha+y})/{\alpha}$
is therefore
$({\alpha+y})/{\alpha}$
is therefore
![]() $({a + \wp(y)})/{a} = 1 + \wp(y)/a$
. Since v is p-henselian, we can choose
$({a + \wp(y)})/{a} = 1 + \wp(y)/a$
. Since v is p-henselian, we can choose
![]() $y \in K$
with
$y \in K$
with
![]() $\wp(y) = (b-1)a = ({b-1})/{x} (ax) \in \mathfrak{m}_v$
. Then
$\wp(y) = (b-1)a = ({b-1})/{x} (ax) \in \mathfrak{m}_v$
. Then
![]() $b = 1 + \wp(y)/a$
is a norm, as desired.
$b = 1 + \wp(y)/a$
is a norm, as desired.
Lemma 4.2. Let v be a non-trivial p-henselian valuation on K. If Kv is imperfect, then the value group vK is countable and has a minimal positive element.
Proof. Let us first argue that the field Kv is countable. Pick
![]() $x \in K$
with
$x \in K$
with
![]() $v(x) < 0$
and consider the
$v(x) < 0$
and consider the
![]() $\mathbb{F}_p$
-linear map
$\mathbb{F}_p$
-linear map
(where
![]() $y \in \mathcal{O}_v$
). This map is well defined since if
$y \in \mathcal{O}_v$
). This map is well defined since if
![]() $y \in z^p + \mathfrak{m}_v$
for some
$y \in z^p + \mathfrak{m}_v$
for some
![]() $z \in \mathcal{O}_v$
, we have
$z \in \mathcal{O}_v$
, we have
This map is also injective. Indeed, if
![]() $y \in \mathcal{O}_v$
is such that
$y \in \mathcal{O}_v$
is such that
![]() $yx^p \in \wp(K) + x^p \mathfrak{m}_v$
, we have
$yx^p \in \wp(K) + x^p \mathfrak{m}_v$
, we have
![]() $y \in \mathfrak{m}_v + x^{-p}\wp(K)$
, so there exists
$y \in \mathfrak{m}_v + x^{-p}\wp(K)$
, so there exists
![]() $z \in K$
with
$z \in K$
with
![]() $y - x^{-p}(z^p-z) \in \mathfrak{m}_v$
. Comparing valuations, we must have
$y - x^{-p}(z^p-z) \in \mathfrak{m}_v$
. Comparing valuations, we must have
![]() $v(z) \geq v(x)$
, and so
$v(z) \geq v(x)$
, and so
![]() $x^{-p}z \in \mathfrak{m}_v$
, yielding
$x^{-p}z \in \mathfrak{m}_v$
, yielding
![]() $y - (z/x)^p \in \mathfrak{m}_v$
. This shows that
$y - (z/x)^p \in \mathfrak{m}_v$
. This shows that
![]() $y + \mathfrak{m}_v \in Kv$
is a pth power, proving that the map has trivial kernel. Since the codomain of the map is a quotient of of
$y + \mathfrak{m}_v \in Kv$
is a pth power, proving that the map has trivial kernel. Since the codomain of the map is a quotient of of
![]() $K/\wp(K)$
and therefore countable by our standing assumption, the positive-dimensional
$K/\wp(K)$
and therefore countable by our standing assumption, the positive-dimensional
![]() $(Kv)^p$
-vector space
$(Kv)^p$
-vector space
![]() $Kv/(Kv)^p$
must also be countable. This shows that
$Kv/(Kv)^p$
must also be countable. This shows that
![]() $(Kv)^p$
and therefore Kv are countable.
$(Kv)^p$
and therefore Kv are countable.
Let
![]() $a \in \mathcal{O}_v$
such that the residue of a in Kv is not a pth power. For every
$a \in \mathcal{O}_v$
such that the residue of a in Kv is not a pth power. For every
![]() $\gamma \in vK$
,
$\gamma \in vK$
,
![]() $\gamma < 0$
, choose an element
$\gamma < 0$
, choose an element
![]() $x_\gamma$
of valuation
$x_\gamma$
of valuation
![]() $\gamma$
, and set
$\gamma$
, and set
![]() $y_\gamma = a x_\gamma^p$
. We claim that the images of the
$y_\gamma = a x_\gamma^p$
. We claim that the images of the
![]() $y_\gamma$
in
$y_\gamma$
in
![]() $K/\wp(K)$
are
$K/\wp(K)$
are
![]() $\mathbb{F}_p$
-linearly independent. Indeed, if they were not, then there would exist
$\mathbb{F}_p$
-linearly independent. Indeed, if they were not, then there would exist
![]() $\gamma_1 < \gamma_2 < \dotsb \gamma_n < 0$
and coefficients
$\gamma_1 < \gamma_2 < \dotsb \gamma_n < 0$
and coefficients
![]() $a_2, \dotsc, a_n \in \mathbb{F}_p$
, as well as an element
$a_2, \dotsc, a_n \in \mathbb{F}_p$
, as well as an element
![]() $z \in K$
with
$z \in K$
with
![]() $y_{\gamma_1} = a_2 y_{\gamma_2} + \dotsb + a_n y_{\gamma_n} + z^p - z$
. Considering the valuation of each term, we must have
$y_{\gamma_1} = a_2 y_{\gamma_2} + \dotsb + a_n y_{\gamma_n} + z^p - z$
. Considering the valuation of each term, we must have
![]() $v(z) = v(y_{\gamma_1})/p = v(x_{\gamma_1})$
. Dividing by
$v(z) = v(y_{\gamma_1})/p = v(x_{\gamma_1})$
. Dividing by
![]() $x_{\gamma_1}^p$
and taking residues, we obtain
$x_{\gamma_1}^p$
and taking residues, we obtain
![]() $\overline{a} = \overline{z/x_{\gamma_1}}^p$
, contradicting the choice of a. This shows the linear independence claimed.
$\overline{a} = \overline{z/x_{\gamma_1}}^p$
, contradicting the choice of a. This shows the linear independence claimed.
In particular, it follows that vK is countable since
![]() $K/\wp(K)$
is countable. Assume now that vK does not have a minimal positive element, so vK is densely ordered. We may then fix a sequence
$K/\wp(K)$
is countable. Assume now that vK does not have a minimal positive element, so vK is densely ordered. We may then fix a sequence
![]() $\delta_1, \delta_2, \dotsc$
of negative elements of vK converging to 0. There exists a family of functions
$\delta_1, \delta_2, \dotsc$
of negative elements of vK converging to 0. There exists a family of functions
![]() $f_i \in \mathbb{N} \to \{0, 1\}$
, indexed by i in some uncountable index set I, such that for
$f_i \in \mathbb{N} \to \{0, 1\}$
, indexed by i in some uncountable index set I, such that for
![]() $i \neq j$
the functions
$i \neq j$
the functions
![]() $f_i$
and
$f_i$
and
![]() $f_j$
differ in infinitely many places. (For instance, for every set P of prime numbers, choose a function f which is 1 at each power of a prime in P and 0 everywhere else.) By the pairing axiom (Pair), and using the linear independence previously proved, there exist elements
$f_j$
differ in infinitely many places. (For instance, for every set P of prime numbers, choose a function f which is 1 at each power of a prime in P and 0 everywhere else.) By the pairing axiom (Pair), and using the linear independence previously proved, there exist elements
![]() $z_i \in K^\times$
, indexed by
$z_i \in K^\times$
, indexed by
![]() $i \in I$
, such that
$i \in I$
, such that
![]() $[{y_{\delta_n}}, {z_i})$
is a non-zero element of
$[{y_{\delta_n}}, {z_i})$
is a non-zero element of
![]() $\text{Br}(K)[p]$
if and only if
$\text{Br}(K)[p]$
if and only if
![]() $f_i(n) = 1$
.
$f_i(n) = 1$
.
The group
![]() $K^\times/(K^{\times p}(1+\mathfrak{m}_v))$
is countable as a group extension of
$K^\times/(K^{\times p}(1+\mathfrak{m}_v))$
is countable as a group extension of
![]() $K^\times/(K^{\times p} \mathcal{O}_v^\times) \cong vK/p$
by
$K^\times/(K^{\times p} \mathcal{O}_v^\times) \cong vK/p$
by
![]() $(K^{\times p} \mathcal{O}_v^\times)/(K^{\times p}(1+\mathfrak{m}_v)) \cong \mathcal{O}_v^\times/(\mathcal{O}_v^{\times p}(1+\mathfrak{m}_v)) \cong (Kv)^\times/p$
, both of which are countable groups by the previous steps. Therefore there must exist two indices
$(K^{\times p} \mathcal{O}_v^\times)/(K^{\times p}(1+\mathfrak{m}_v)) \cong \mathcal{O}_v^\times/(\mathcal{O}_v^{\times p}(1+\mathfrak{m}_v)) \cong (Kv)^\times/p$
, both of which are countable groups by the previous steps. Therefore there must exist two indices
![]() $i \neq j$
such that
$i \neq j$
such that
![]() $z_i/z_j \in K^{\times p} (1 + \mathfrak{m}_v)$
, so we may write
$z_i/z_j \in K^{\times p} (1 + \mathfrak{m}_v)$
, so we may write
![]() $z_i/z_j = a^p (1 + b)$
for suitable
$z_i/z_j = a^p (1 + b)$
for suitable
![]() $a \in K^\times$
,
$a \in K^\times$
,
![]() $b \in \mathfrak{m}_v$
.
$b \in \mathfrak{m}_v$
.
Since the
![]() $\delta_n$
converge to 0, there exists an
$\delta_n$
converge to 0, there exists an
![]() $n_0$
such that for all
$n_0$
such that for all
![]() $n \geq n_0$
we have
$n \geq n_0$
we have
![]() $\delta_n > -v(b)$
, and therefore
$\delta_n > -v(b)$
, and therefore
by Lemma 4.1 (set
![]() $x = x_{\delta_n}^{-1}$
there). This forces
$x = x_{\delta_n}^{-1}$
there). This forces
![]() $f_i(n) = f_j(n)$
for all
$f_i(n) = f_j(n)$
for all
![]() $n \geq n_0$
, contradicting our choice of functions
$n \geq n_0$
, contradicting our choice of functions
![]() $f_i$
.
$f_i$
.
Lemma 4.3. Let v be a non-trivial p-henselian valuation on K whose residue field Kv is not p-closed. Suppose that Kv is perfect and vK has no non-trivial p-divisible convex subgroup. Then vK is countable and has a minimal positive element.
Proof. Let us first prove that vK is countable. Pick
![]() $\gamma \in vK$
,
$\gamma \in vK$
,
![]() $\gamma < 0$
, which is not in
$\gamma < 0$
, which is not in
![]() $p \cdot vK$
. Fix
$p \cdot vK$
. Fix
![]() $x \in K$
with
$x \in K$
with
![]() $vx = \gamma$
. For every
$vx = \gamma$
. For every
![]() $\delta \in vK$
,
$\delta \in vK$
,
![]() $\delta < 0$
, choose
$\delta < 0$
, choose
![]() $y_\delta \in K$
with
$y_\delta \in K$
with
![]() $vy_\delta = \delta$
, and set
$vy_\delta = \delta$
, and set
![]() $x_\delta = x y_\delta^p$
. Since the elements
$x_\delta = x y_\delta^p$
. Since the elements
![]() $x_\delta$
have distinct negative valuations not divisible by p, no non-trivial
$x_\delta$
have distinct negative valuations not divisible by p, no non-trivial
![]() $\mathbb{F}_p$
-linear combination of the
$\mathbb{F}_p$
-linear combination of the
![]() $x_\delta$
can lie in
$x_\delta$
can lie in
![]() $\wp(K)$
. Therefore the elements
$\wp(K)$
. Therefore the elements
![]() $x_\delta + \wp(K)$
are
$x_\delta + \wp(K)$
are
![]() $\mathbb{F}_p$
-linearly independent in
$\mathbb{F}_p$
-linearly independent in
![]() $K/\wp(K)$
. Since the latter is countable by our standing assumption, this shows that vK is countable.
$K/\wp(K)$
. Since the latter is countable by our standing assumption, this shows that vK is countable.
Suppose now that vK has no minimal positive element, so that vK is densely ordered. Since vK has no non-trivial p-divisible convex subgroup, every open interval in vK containing 0 contains elements which are not p-divisible. We can therefore choose a sequence
![]() $\delta_1, \delta_2, \dotsc$
of negative elements of vK which converges to 0 and such that no
$\delta_1, \delta_2, \dotsc$
of negative elements of vK which converges to 0 and such that no
![]() $\delta_i$
is divisible by p.
$\delta_i$
is divisible by p.
For every n, let
![]() $x_n \in K$
with
$x_n \in K$
with
![]() $vx_n = \delta_n$
. As above, the elements
$vx_n = \delta_n$
. As above, the elements
![]() $x_n + \mathcal{O}_v + \wp(K) \in K/(\mathcal{O}_v + \wp(K))$
are
$x_n + \mathcal{O}_v + \wp(K) \in K/(\mathcal{O}_v + \wp(K))$
are
![]() $\mathbb{F}_p$
-linearly independent. Consequently there exists an
$\mathbb{F}_p$
-linearly independent. Consequently there exists an
![]() $\mathbb{F}_p$
-linear map
$\mathbb{F}_p$
-linear map
![]() $f \colon K/\wp(K) \to \text{Br}(K)[p]$
with
$f \colon K/\wp(K) \to \text{Br}(K)[p]$
with
![]() $f(\mathcal{O}_v) = 0$
and
$f(\mathcal{O}_v) = 0$
and
![]() $f(x_n) \neq 0$
for each n. By the pairing axiom (Pair), there exists
$f(x_n) \neq 0$
for each n. By the pairing axiom (Pair), there exists
![]() $z \in K^\times$
with
$z \in K^\times$
with
![]() $\left[{\cdot}, {z}\right) = f$
, so that
$\left[{\cdot}, {z}\right) = f$
, so that
![]() $\left[{\mathcal{O}_v}, {z}\right) = 0$
and
$\left[{\mathcal{O}_v}, {z}\right) = 0$
and
![]() $\left[{x_n}, {z}\right) \neq 0$
for each n.
$\left[{x_n}, {z}\right) \neq 0$
for each n.
By assumption Kv is not p-closed, so there exists an element
![]() $a \in \mathcal{O}_v$
whose residue does not lie in
$a \in \mathcal{O}_v$
whose residue does not lie in
![]() $\wp(Kv)$
. This means that
$\wp(Kv)$
. This means that
![]() $a \not\in \wp(K)$
, and so adjoining a root of
$a \not\in \wp(K)$
, and so adjoining a root of
![]() $X^p-X-a$
to K yields a
$X^p-X-a$
to K yields a
![]() $\mathbb{Z}/p$
-extension
$\mathbb{Z}/p$
-extension
![]() $L/K$
by Artin–Schreier theory. The valuation v extends uniquely to L by p-henselianity, and the residue field of L is a proper extension of the residue field Kv, since it contains an Artin–Schreier root of the residue of a, but by assumption Kv does not. Therefore the value group does not change in the degree p extension
$L/K$
by Artin–Schreier theory. The valuation v extends uniquely to L by p-henselianity, and the residue field of L is a proper extension of the residue field Kv, since it contains an Artin–Schreier root of the residue of a, but by assumption Kv does not. Therefore the value group does not change in the degree p extension
![]() $L/K$
by [Reference Engler and PrestelEP05, Theorem 3.3.3]. Since
$L/K$
by [Reference Engler and PrestelEP05, Theorem 3.3.3]. Since
![]() $\left[{\mathcal{O}_v}, {z}\right) = 0$
, Lemma 2.1 (applied to the homomorphism
$\left[{\mathcal{O}_v}, {z}\right) = 0$
, Lemma 2.1 (applied to the homomorphism
![]() $\chi \colon \text{G}_K \to \mathbb{Z}/p$
corresponding to a under the Artin–Schreier isomorphism
$\chi \colon \text{G}_K \to \mathbb{Z}/p$
corresponding to a under the Artin–Schreier isomorphism
![]() $\text{Hom}(\text{G}_K,\mathbb{Z}/p) \cong K/\wp(K)$
, whose kernel is
$\text{Hom}(\text{G}_K,\mathbb{Z}/p) \cong K/\wp(K)$
, whose kernel is
![]() $\text{G}_L$
) implies that z is a norm of the extension
$\text{G}_L$
) implies that z is a norm of the extension
![]() $L/K$
. It now follows from [Reference Engler and PrestelEP05, Remark 3.2.17] that the valuation of z must be divisible by p. Hence we may as well suppose that
$L/K$
. It now follows from [Reference Engler and PrestelEP05, Remark 3.2.17] that the valuation of z must be divisible by p. Hence we may as well suppose that
![]() $z \in \mathcal{O}_v^\times$
by multiplying z by a pth power.
$z \in \mathcal{O}_v^\times$
by multiplying z by a pth power.
Since Kv is perfect, we may further suppose that
![]() $z \in 1 + \mathfrak{m}_v$
. However, Lemma 4.1 now implies that for all n with
$z \in 1 + \mathfrak{m}_v$
. However, Lemma 4.1 now implies that for all n with
![]() $v(x_n) > -v(z-1)$
we have
$v(x_n) > -v(z-1)$
we have
![]() $\left[{x_n}, {z}\right) = 0$
; since the values
$\left[{x_n}, {z}\right) = 0$
; since the values
![]() $v(x_n)$
converge to 0, this is the case for all sufficiently large n, contradicting the choice of z.
$v(x_n)$
converge to 0, this is the case for all sufficiently large n, contradicting the choice of z.
As usual, an element of a valued field whose valuation is minimal positive is called a uniformiser.
Lemma 4.4. Let v be a non-trivial p-henselian valuation on K with a uniformiser
![]() $\pi$
and such that Kv is not p-closed. Then the residue field Kv is finite.
$\pi$
and such that Kv is not p-closed. Then the residue field Kv is finite.
Proof. By Lemma 4.2 and Lemma 4.3 the value group vK is countable. The embedding
![]() $({1}/{\pi})\mathcal{O}_v \hookrightarrow K$
induces an injection
$({1}/{\pi})\mathcal{O}_v \hookrightarrow K$
induces an injection
![]() $({1}/{\pi})\mathcal{O}_v/\wp(\mathcal{O}_v) \hookrightarrow K/\wp(K)$
of
$({1}/{\pi})\mathcal{O}_v/\wp(\mathcal{O}_v) \hookrightarrow K/\wp(K)$
of
![]() $\mathbb{F}_p$
-vector spaces, which in turn induces a surjective linear map
$\mathbb{F}_p$
-vector spaces, which in turn induces a surjective linear map
![]() $\text{Hom}(K/\wp(K), \text{Br}(K)[p]) \to \text{Hom}(({1}/{\pi})\mathcal{O}_v/\wp(\mathcal{O}_v), \text{Br}(K)[p])$
. We therefore obtain a surjective group homomorphism
$\text{Hom}(K/\wp(K), \text{Br}(K)[p]) \to \text{Hom}(({1}/{\pi})\mathcal{O}_v/\wp(\mathcal{O}_v), \text{Br}(K)[p])$
. We therefore obtain a surjective group homomorphism
where the first map is induced by the pairing function and is surjective by the pairing axiom (Pair). The group
![]() $1 + \pi^2\mathcal{O}_v/(K^{\times p} \cap (1 + \pi^2\mathcal{O}_v))$
lies in the kernel by Lemma 4.1, so we obtain a surjective homomorphism
$1 + \pi^2\mathcal{O}_v/(K^{\times p} \cap (1 + \pi^2\mathcal{O}_v))$
lies in the kernel by Lemma 4.1, so we obtain a surjective homomorphism
Suppose Kv has infinite dimension
![]() $\kappa$
as an
$\kappa$
as an
![]() $\mathbb{F}_p$
-vector space. Then
$\mathbb{F}_p$
-vector space. Then
![]() $({1}/{\pi})\mathcal{O}_v/\wp(\mathcal{O}_v)$
also has dimension at least
$({1}/{\pi})\mathcal{O}_v/\wp(\mathcal{O}_v)$
also has dimension at least
![]() $\kappa$
, since it has
$\kappa$
, since it has
![]() $({1}/{\pi})\mathcal{O}_v/\mathcal{O}_v \cong Kv$
as a quotient. Consequently
$({1}/{\pi})\mathcal{O}_v/\mathcal{O}_v \cong Kv$
as a quotient. Consequently
![]() $\text{Hom}(({1}/{\pi})\mathcal{O}_v/\wp(\mathcal{O}_v), \text{Br}(K)[p])$
has cardinality at least
$\text{Hom}(({1}/{\pi})\mathcal{O}_v/\wp(\mathcal{O}_v), \text{Br}(K)[p])$
has cardinality at least
![]() $2^\kappa$
, as we can construct homomorphisms by freely choosing images of some fixed basis vectors.
$2^\kappa$
, as we can construct homomorphisms by freely choosing images of some fixed basis vectors.
On the other hand,
![]() $K^\times/(K^{\times p} (1 + \pi^2 \mathcal{O}_v))$
has cardinality at most
$K^\times/(K^{\times p} (1 + \pi^2 \mathcal{O}_v))$
has cardinality at most
![]() $\kappa$
. Indeed, in the subgroup series
$\kappa$
. Indeed, in the subgroup series
the first factor group
![]() $K^\times/(K^{\times p} \mathcal{O}_v^\times) \cong vK/p$
is countable, the second factor group
$K^\times/(K^{\times p} \mathcal{O}_v^\times) \cong vK/p$
is countable, the second factor group
has cardinality at most
![]() $\kappa$
, and the third factor group
$\kappa$
, and the third factor group
![]() $(K^{\times p} (1 + \pi \mathcal{O}_v)) / (K^{\times p} (1 + \pi^2 \mathcal{O}_v))$
has cardinality at most
$(K^{\times p} (1 + \pi \mathcal{O}_v)) / (K^{\times p} (1 + \pi^2 \mathcal{O}_v))$
has cardinality at most
![]() $\kappa$
since it has a surjection from
$\kappa$
since it has a surjection from
![]() $(1 + \pi \mathcal{O}_v)/(1 + \pi^2 \mathcal{O}_v) \cong Kv$
. This shows that
$(1 + \pi \mathcal{O}_v)/(1 + \pi^2 \mathcal{O}_v) \cong Kv$
. This shows that
![]() $K^\times/(K^{\times p} (1 + \pi^2 \mathcal{O}_v))$
has cardinality at most
$K^\times/(K^{\times p} (1 + \pi^2 \mathcal{O}_v))$
has cardinality at most
![]() $\kappa$
. Since we cannot have a surjective map from a set of cardinality at most
$\kappa$
. Since we cannot have a surjective map from a set of cardinality at most
![]() $\kappa$
to one of cardinality at least
$\kappa$
to one of cardinality at least
![]() $2^\kappa$
, this is a contradiction.
$2^\kappa$
, this is a contradiction.
Lemma 4.5. If K carries a non-trivial p-henselian valuation v with Kv not p-closed, then Kv is finite and vK is isomorphic to
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
Proof. If the residue field Kv is not perfect, then by Lemma 4.2 there exists a uniformiser and by Lemma 4.4 the residue field Kv is finite and therefore perfect after all.
Thus the residue field Kv is perfect. If the value group vK is p-divisible, every element of
![]() $K^\times$
can be written as the product of a pth power with an element of
$K^\times$
can be written as the product of a pth power with an element of
![]() $1 + \mathfrak{m}_v$
. Lemma 4.1 implies that then
$1 + \mathfrak{m}_v$
. Lemma 4.1 implies that then
![]() $\left[{\mathcal{O}_v}, {K^\times}\right) = 0$
. By the pairing axiom (Pair), this is only possible if
$\left[{\mathcal{O}_v}, {K^\times}\right) = 0$
. By the pairing axiom (Pair), this is only possible if
![]() $\mathcal{O}_v \subseteq \wp(K)$
, implying that
$\mathcal{O}_v \subseteq \wp(K)$
, implying that
![]() $Kv = \wp(Kv)$
, but this is in contradiction to the assumption that Kv is not p-closed. Therefore the value group vK is not p-divisible. Let w be the coarsening of v corresponding to the largest p-divisible convex subgroup of vK.
$Kv = \wp(Kv)$
, but this is in contradiction to the assumption that Kv is not p-closed. Therefore the value group vK is not p-divisible. Let w be the coarsening of v corresponding to the largest p-divisible convex subgroup of vK.
Since Kv has a
![]() $\mathbb{Z}/p$
-extension by assumption, there exists a
$\mathbb{Z}/p$
-extension by assumption, there exists a
![]() $\mathbb{Z}/p$
-extension of K which is unramified with respect to v, and in particular unramified with respect to w, so Kw is not p-closed. Repeating the previous argument with (K,w), we see that the residue field Kw is perfect. By Lemma 4.3 (K,w) has a uniformiser
$\mathbb{Z}/p$
-extension of K which is unramified with respect to v, and in particular unramified with respect to w, so Kw is not p-closed. Repeating the previous argument with (K,w), we see that the residue field Kw is perfect. By Lemma 4.3 (K,w) has a uniformiser
![]() $\pi$
, and by Lemma 4.4 its residue field Kw is finite. In particular, v cannot be a proper refinement of w, so
$\pi$
, and by Lemma 4.4 its residue field Kw is finite. In particular, v cannot be a proper refinement of w, so
![]() $w = v$
.
$w = v$
.
The subgroup of vK generated by the value of the uniformiser
![]() $\pi$
is isomorphic to
$\pi$
is isomorphic to
![]() $\mathbb{Z}$
and convex. Consider the coarsening v’ of v with value group
$\mathbb{Z}$
and convex. Consider the coarsening v’ of v with value group
![]() $v'K = vK/\langle v(\pi)\rangle$
(i.e. the finest proper coarsening of v). The residue field Kv’ carries a valuation with value group
$v'K = vK/\langle v(\pi)\rangle$
(i.e. the finest proper coarsening of v). The residue field Kv’ carries a valuation with value group
![]() $\mathbb{Z}$
, and so Kv’ is imperfect. As above, Kv’ is also not p-closed. If v’ is not the trivial valuation, then Lemma 4.2 and Lemma 4.4 imply that Kv’ is finite, which is absurd. Therefore v’ must be trivial, and vK is isomorphic to
$\mathbb{Z}$
, and so Kv’ is imperfect. As above, Kv’ is also not p-closed. If v’ is not the trivial valuation, then Lemma 4.2 and Lemma 4.4 imply that Kv’ is finite, which is absurd. Therefore v’ must be trivial, and vK is isomorphic to
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
Lemma 4.6. In the situation of the previous lemma, the natural group homomorphism
![]() $K^\times/p \to \widehat{K}^\times/p$
is an isomorphism, where
$K^\times/p \to \widehat{K}^\times/p$
is an isomorphism, where
![]() $\widehat{K}$
is the completion of K with respect to v.
$\widehat{K}$
is the completion of K with respect to v.
Proof. Let
![]() $\pi \in K$
be a uniformiser. The completion
$\pi \in K$
be a uniformiser. The completion
![]() $\widehat{K}$
is isomorphic to
$\widehat{K}$
is isomorphic to
![]() $\mathbb{F}_q(\!(t)\!)$
for suitable
$\mathbb{F}_q(\!(t)\!)$
for suitable
![]() $\mathbb{F}_q = Kv$
, where the isomorphism sends
$\mathbb{F}_q = Kv$
, where the isomorphism sends
![]() $\pi$
to t. We obtain the following diagram.
$\pi$
to t. We obtain the following diagram.

By the construction of the pairing, this diagram is commutative. The map
![]() $K/\wp(K) \to \widehat{K}/\wp(\widehat{K})$
is surjective since K is dense in
$K/\wp(K) \to \widehat{K}/\wp(\widehat{K})$
is surjective since K is dense in
![]() $\widehat{K}$
and
$\widehat{K}$
and
![]() $\wp(\widehat{K})$
is open, as
$\wp(\widehat{K})$
is open, as
![]() $\wp(\widehat{K}) \supseteq \widehat{\mathfrak{m}}_v$
by Hensel’s Lemma. It is also injective since
$\wp(\widehat{K}) \supseteq \widehat{\mathfrak{m}}_v$
by Hensel’s Lemma. It is also injective since
![]() $\wp(\widehat{K}) = \wp(K) + \widehat{\mathfrak{m}}_v$
, and
$\wp(\widehat{K}) = \wp(K) + \widehat{\mathfrak{m}}_v$
, and
![]() $\widehat{\mathfrak{m}}_v \cap K = \mathfrak{m}_v \subseteq \wp(K)$
by the p-henselianity assumption. The map
$\widehat{\mathfrak{m}}_v \cap K = \mathfrak{m}_v \subseteq \wp(K)$
by the p-henselianity assumption. The map
![]() $\text{Br}(K)[p] \to \text{Br}(\widehat{K})[p]$
is an isomorphism since both sides are isomorphic to
$\text{Br}(K)[p] \to \text{Br}(\widehat{K})[p]$
is an isomorphism since both sides are isomorphic to
![]() $\mathbb{Z}/p$
and the image of
$\mathbb{Z}/p$
and the image of
![]() $\left[{\mathcal{O}_v}, {\pi}\right)$
in
$\left[{\mathcal{O}_v}, {\pi}\right)$
in
![]() $\text{Br}(\widehat{K})[p]$
is non-zero by standard facts on the Brauer group of local fields (cf. [Reference Gille and SzamuelyGS17, Remark 6.3.6]).
$\text{Br}(\widehat{K})[p]$
is non-zero by standard facts on the Brauer group of local fields (cf. [Reference Gille and SzamuelyGS17, Remark 6.3.6]).
Using the pairing axiom (Pair) for both K and
![]() $\widehat{K}$
(where it holds by Proposition 2.2), we obtain that
$\widehat{K}$
(where it holds by Proposition 2.2), we obtain that
![]() $K^\times/p \to \widehat{K}^\times/p$
is an isomorphism.
$K^\times/p \to \widehat{K}^\times/p$
is an isomorphism.
Proposition 4.7. Suppose, beyond the standing assumptions of this section, that
![]() $[K : K^p] \leq p$
. Let v be a non-trivial p-henselian valuation on K with Kv not p-closed. Then (K, v) is a complete discretely valued field with finite residue field, i.e. a local field.
$[K : K^p] \leq p$
. Let v be a non-trivial p-henselian valuation on K with Kv not p-closed. Then (K, v) is a complete discretely valued field with finite residue field, i.e. a local field.
Proof. Applying Lemma 4.5, it only remains to show that
![]() $K = \widehat{K}$
, i.e. (K,v) is complete. Let
$K = \widehat{K}$
, i.e. (K,v) is complete. Let
![]() $\pi$
be a uniformiser of (K,v). For
$\pi$
be a uniformiser of (K,v). For
![]() $x \in \widehat{K}$
, consider the element
$x \in \widehat{K}$
, consider the element
![]() $1 + \pi x^p$
. Since
$1 + \pi x^p$
. Since
![]() $K^\times/p \to \widehat{K}^\times/p$
is an isomorphism by Lemma 4.6, there exist
$K^\times/p \to \widehat{K}^\times/p$
is an isomorphism by Lemma 4.6, there exist
![]() $y \in K$
and
$y \in K$
and
![]() $z \in \widehat{K}^\times$
with
$z \in \widehat{K}^\times$
with
![]() $y = z^p(1 + \pi x^p)$
. By the assumption
$y = z^p(1 + \pi x^p)$
. By the assumption
![]() $[K : K^p] \leq p$
, the element
$[K : K^p] \leq p$
, the element
![]() $\pi$
of K is a p-basis, and so we may write
$\pi$
of K is a p-basis, and so we may write
![]() $y = y_0^p + \pi y_1^p + \dotsb + \pi^{p-1} y_{p-1}^p$
with elements
$y = y_0^p + \pi y_1^p + \dotsb + \pi^{p-1} y_{p-1}^p$
with elements
![]() $y_i \in K$
. We have thus obtained the equation
$y_i \in K$
. We have thus obtained the equation
Since
![]() $\pi$
is also a p-basis of the field
$\pi$
is also a p-basis of the field
![]() $\widehat{K}$
, we can compare coefficients to obtain
$\widehat{K}$
, we can compare coefficients to obtain
![]() $z = y_0 \in K$
and
$z = y_0 \in K$
and
![]() $y_1 = zx$
, so in particular
$y_1 = zx$
, so in particular
![]() $x = y_1/y_0 \in K$
, as desired.
$x = y_1/y_0 \in K$
, as desired.
Remark 4.8. The additional assumption
![]() $[K : K^p] \leq p$
cannot be dispensed with, as the following construction due to Arno Fehm shows.
$[K : K^p] \leq p$
cannot be dispensed with, as the following construction due to Arno Fehm shows.
Consider the local field
![]() $\mathbb{F}_q(\!(t)\!)$
and enumerate its elements as
$\mathbb{F}_q(\!(t)\!)$
and enumerate its elements as
![]() $(x_\alpha)_{\alpha < 2^{\aleph_0}}$
. Let
$(x_\alpha)_{\alpha < 2^{\aleph_0}}$
. Let
![]() $s \in \mathbb{F}_q(\!(t)\!)$
be an element such that s and t are algebraically independent. We construct an increasing chain of subfields
$s \in \mathbb{F}_q(\!(t)\!)$
be an element such that s and t are algebraically independent. We construct an increasing chain of subfields
![]() $K_\beta$
of
$K_\beta$
of
![]() $\mathbb{F}_q(\!(t)\!)$
indexed by
$\mathbb{F}_q(\!(t)\!)$
indexed by
![]() $\beta < 2^{\aleph_0}$
, where
$\beta < 2^{\aleph_0}$
, where
![]() $K_0 = \mathbb{F}_q(t)$
, every
$K_0 = \mathbb{F}_q(t)$
, every
![]() $K_\beta$
has cardinality strictly less than
$K_\beta$
has cardinality strictly less than
![]() $2^{\aleph_0}$
,
$2^{\aleph_0}$
,
![]() $K_\beta$
is relatively algebraically closed in
$K_\beta$
is relatively algebraically closed in
![]() $\mathbb{F}_q(\!(t)\!)$
, the image of the map
$\mathbb{F}_q(\!(t)\!)$
, the image of the map
![]() $K_\beta^\times/p \to \mathbb{F}_q(\!(t)\!)^\times/p$
contains the pth power classes of all
$K_\beta^\times/p \to \mathbb{F}_q(\!(t)\!)^\times/p$
contains the pth power classes of all
![]() $x_\alpha$
with
$x_\alpha$
with
![]() $\alpha < \beta$
, and s is transcendental over
$\alpha < \beta$
, and s is transcendental over
![]() $K_\beta$
. This can be done straightforwardly by transfinite induction: at limit ordinals
$K_\beta$
. This can be done straightforwardly by transfinite induction: at limit ordinals
![]() $\beta$
one takes
$\beta$
one takes
![]() $K_\beta := \bigcup_{\gamma < \beta} K_\gamma$
, and for a successor ordinal
$K_\beta := \bigcup_{\gamma < \beta} K_\gamma$
, and for a successor ordinal
![]() $\beta+1$
one takes
$\beta+1$
one takes
![]() $K_{\beta+1}$
to be the relative algebraic closure of
$K_{\beta+1}$
to be the relative algebraic closure of
![]() $K_\beta(x)$
for a suitably chosen element x in the pth power class
$K_\beta(x)$
for a suitably chosen element x in the pth power class
![]() $x_\beta \mathbb{F}_q(\!(t)\!)^{\times p}$
of
$x_\beta \mathbb{F}_q(\!(t)\!)^{\times p}$
of
![]() $x_\beta$
. The only constraint is ensuring that s remains transcendental over
$x_\beta$
. The only constraint is ensuring that s remains transcendental over
![]() $K_{\beta+1}$
; to do so, it suffices to pick x not algebraic over
$K_{\beta+1}$
; to do so, it suffices to pick x not algebraic over
![]() $K_\beta(s)$
, which can always be done since
$K_\beta(s)$
, which can always be done since
![]() $x_\beta \mathbb{F}_q(\!(t)\!)^{\times p}$
has strictly larger cardinality than
$x_\beta \mathbb{F}_q(\!(t)\!)^{\times p}$
has strictly larger cardinality than
![]() $K_\beta(s)$
.
$K_\beta(s)$
.
Now the field
![]() $K = \bigcup_{\beta < 2^{\aleph_0}} K_\beta$
is relatively algebraically closed in
$K = \bigcup_{\beta < 2^{\aleph_0}} K_\beta$
is relatively algebraically closed in
![]() $\mathbb{F}_q(\!(t)\!)$
, the map
$\mathbb{F}_q(\!(t)\!)$
, the map
![]() $K^\times/p \to \mathbb{F}_q(\!(t)\!)^\times/p$
is an isomorphism (surjectivity is by construction, and injectivity follows from relative algebraic closedness), but K does not contain s. The restriction map of absolute Galois groups
$K^\times/p \to \mathbb{F}_q(\!(t)\!)^\times/p$
is an isomorphism (surjectivity is by construction, and injectivity follows from relative algebraic closedness), but K does not contain s. The restriction map of absolute Galois groups
![]() $\text{G}_{\mathbb{F}_q(\!(t)\!)} \to \text{G}_K$
is an isomorphism: here surjectivity follows from relative algebraic closedness, and injectivity holds since the restriction map
$\text{G}_{\mathbb{F}_q(\!(t)\!)} \to \text{G}_K$
is an isomorphism: here surjectivity follows from relative algebraic closedness, and injectivity holds since the restriction map
![]() $\text{G}_{\mathbb{F}_q(\!(t)\!)} \to \text{G}_{\mathbb{F}_q(t)}$
is injective by Krasner’s Lemma [Reference EfratEfr06, Corollary 18.5.3]. Furthermore, the restriction map of Brauer groups
$\text{G}_{\mathbb{F}_q(\!(t)\!)} \to \text{G}_{\mathbb{F}_q(t)}$
is injective by Krasner’s Lemma [Reference EfratEfr06, Corollary 18.5.3]. Furthermore, the restriction map of Brauer groups
![]() $\text{Br}(K) \to \text{Br}(\mathbb{F}_q(\!(t)\!))$
is an isomorphism, as
$\text{Br}(K) \to \text{Br}(\mathbb{F}_q(\!(t)\!))$
is an isomorphism, as
![]() $\text{Br}(K)$
is known from the general theory of the Brauer group [Reference GrothendieckGro68, Corollaire 2.3].
$\text{Br}(K)$
is known from the general theory of the Brauer group [Reference GrothendieckGro68, Corollaire 2.3].
Hence K is a counterexample to Proposition 4.7 when the condition
![]() $[K : K^p] \leq p$
is dropped, and even to Theorem 1.1 without the axiom (Imp). Indeed, K is not isomorphic to a local field, since it carries a unique non-trivial henselian valuation (namely the restriction of the t-adic valuation on
$[K : K^p] \leq p$
is dropped, and even to Theorem 1.1 without the axiom (Imp). Indeed, K is not isomorphic to a local field, since it carries a unique non-trivial henselian valuation (namely the restriction of the t-adic valuation on
![]() $\mathbb{F}_q(\!(t)\!)$
) but is not complete.
$\mathbb{F}_q(\!(t)\!)$
) but is not complete.
Remark 4.9. The condition
![]() $[K : K^p] \leq p$
can be replaced by some alternatives. For instance, let us instead suppose that every purely inseparable extension
$[K : K^p] \leq p$
can be replaced by some alternatives. For instance, let us instead suppose that every purely inseparable extension
![]() $L/K$
of degree p also satisfies the axioms (Brau) and (Pair). Then by applying Lemma 4.6, we see that for every such L the map
$L/K$
of degree p also satisfies the axioms (Brau) and (Pair). Then by applying Lemma 4.6, we see that for every such L the map
![]() $L^\times/p \to (L\widehat{K})^\times/p$
must be an isomorphism, and so in particular L is relatively inseparably closed in
$L^\times/p \to (L\widehat{K})^\times/p$
must be an isomorphism, and so in particular L is relatively inseparably closed in
![]() $L\widehat{K}$
. For a uniformiser
$L\widehat{K}$
. For a uniformiser
![]() $\pi$
of K we obtain, in particular, that
$\pi$
of K we obtain, in particular, that
![]() $K(\sqrt[p]{\pi})$
is relatively inseparably closed in
$K(\sqrt[p]{\pi})$
is relatively inseparably closed in
![]() $\widehat{K}(\sqrt[p]{\pi}) = \widehat{K}^{1/p}$
, implying that
$\widehat{K}(\sqrt[p]{\pi}) = \widehat{K}^{1/p}$
, implying that
![]() $K(\sqrt[p]{\pi}) = K^{1/p}$
, so
$K(\sqrt[p]{\pi}) = K^{1/p}$
, so
![]() $[K : K^p] = [K^{1/p} : K] = p$
.
$[K : K^p] = [K^{1/p} : K] = p$
.
We can now prove the main theorem from the introduction.
Proof of Theorem 1.1. Let K be a field satisfying all the hypotheses. Then by Corollary 3.3 and Proposition 4.7, K is a local field of characteristic p, i.e.
![]() $K \cong \mathbb{F}_{q'}(\!(t)\!)$
for some power q’ of p. Since the t-adic valuation on
$K \cong \mathbb{F}_{q'}(\!(t)\!)$
for some power q’ of p. Since the t-adic valuation on
![]() $\mathbb{F}_{q'}(\!(t)\!)$
is the unique non-trivial henselian valuation on this field by F. K. Schmidt’s Theorem [Reference Engler and PrestelEP05, Theorem 4.4.1], Proposition 3.2 shows that we must have
$\mathbb{F}_{q'}(\!(t)\!)$
is the unique non-trivial henselian valuation on this field by F. K. Schmidt’s Theorem [Reference Engler and PrestelEP05, Theorem 4.4.1], Proposition 3.2 shows that we must have
![]() $q' = q$
.
$q' = q$
.
5. Sharpenings using quotients of the absolute Galois group
Let us observe the ways in which the axiom
![]() $\text{G}_K \cong \text{G}_{\mathbb{F}_q(\!(t)\!)}$
was used in the proof of Theorem 1.1. We established that K has characteristic p in Lemma 2.3, since the p-Sylow subgroups of
$\text{G}_K \cong \text{G}_{\mathbb{F}_q(\!(t)\!)}$
was used in the proof of Theorem 1.1. We established that K has characteristic p in Lemma 2.3, since the p-Sylow subgroups of
![]() $\text{G}_K$
are projective, and used Corollary 3.3 to obtain a valuation on K. Throughout § 4 we relied on K having countably many
$\text{G}_K$
are projective, and used Corollary 3.3 to obtain a valuation on K. Throughout § 4 we relied on K having countably many
![]() $\mathbb{Z}/p$
-extensions, i.e.
$\mathbb{Z}/p$
-extensions, i.e.
![]() $\text{Hom}(\text{G}_K, \mathbb{Z}/p)$
being countable. Lastly, we finished the proof by observing that non-isomorphic local fields of characteristic p have non-isomorphic absolute Galois groups.
$\text{Hom}(\text{G}_K, \mathbb{Z}/p)$
being countable. Lastly, we finished the proof by observing that non-isomorphic local fields of characteristic p have non-isomorphic absolute Galois groups.
The last two of these four uses of the axiom actually need much weaker information than the isomorphism of full absolute Galois groups
![]() $\text{G}_K \cong \text{G}_{\mathbb{F}_q(\!(t)\!)}$
. Indeed, the information about
$\text{G}_K \cong \text{G}_{\mathbb{F}_q(\!(t)\!)}$
. Indeed, the information about
![]() $\mathbb{Z}/p$
-extensions is contained in
$\mathbb{Z}/p$
-extensions is contained in
![]() $\text{G}_K^{\mathrm{ab}}$
, and likewise non-isomorphic local fields of characteristic p have non-isomorphic abelianised absolute Galois groups by [Reference Neukirch, Schmidt and WingbergNSW08, Proposition 7.5.9].
$\text{G}_K^{\mathrm{ab}}$
, and likewise non-isomorphic local fields of characteristic p have non-isomorphic abelianised absolute Galois groups by [Reference Neukirch, Schmidt and WingbergNSW08, Proposition 7.5.9].
In this section we want to show that Lemma 2.3 and Corollary 3.3 also have versions in which the hypothesis only refers to certain quotients of
![]() $\text{G}_K$
. The main tool to achieve this is [Reference Chebolu, Efrat and MináčCEM12]. The proofs here make slightly more serious use of Galois cohomology and Milnor K-groups than the preceding sections, so we assume a passing familiarity with the definitions and basic properties on the part of the reader.
$\text{G}_K$
. The main tool to achieve this is [Reference Chebolu, Efrat and MináčCEM12]. The proofs here make slightly more serious use of Galois cohomology and Milnor K-groups than the preceding sections, so we assume a passing familiarity with the definitions and basic properties on the part of the reader.
Following [Reference Chebolu, Efrat and MináčCEM12, § 4], given a profinite group G and a prime p, we write
![]() $G^{[3,p]}$
for the quotient
$G^{[3,p]}$
for the quotient
![]() $G/((G^p[G,G])^p [G^p[G,G], G])$
, i.e. the quotient of G by the third term in its lower p-central series (also called its descending p-central sequence). Observe that
$G/((G^p[G,G])^p [G^p[G,G], G])$
, i.e. the quotient of G by the third term in its lower p-central series (also called its descending p-central sequence). Observe that
![]() $G^{[3,p]}$
is a pro-p group which is nilpotent of class 2 as a central extension of
$G^{[3,p]}$
is a pro-p group which is nilpotent of class 2 as a central extension of
![]() $G/(G^p[G,G])$
by
$G/(G^p[G,G])$
by
![]() $G^p[G,G]/((G^p[G,G])^p [G^p[G,G], G])$
.
$G^p[G,G]/((G^p[G,G])^p [G^p[G,G], G])$
.
Lemma 5.1. Let p be a prime number, and let K be a field such that
![]() $\text{Br}(K)[p] \neq 0$
and the absolute Galois group
$\text{Br}(K)[p] \neq 0$
and the absolute Galois group
![]() $\text{G}_K$
satisfies the following: for every open normal subgroup H of
$\text{G}_K$
satisfies the following: for every open normal subgroup H of
![]() $\text{G}_K$
with cyclic quotient
$\text{G}_K$
with cyclic quotient
![]() $\text{G}_K/H$
of order dividing
$\text{G}_K/H$
of order dividing
![]() $p-1$
,
$p-1$
,
![]() $H^{[3,p]} \cong F^{[3,p]}$
for some free pro-p group F. Then K has characteristic p.
$H^{[3,p]} \cong F^{[3,p]}$
for some free pro-p group F. Then K has characteristic p.
Conversely, every field K of characteristic p satisfies the condition on
![]() $\text{G}_K$
.
$\text{G}_K$
.
Proof. Suppose first that K is of characteristic p. Let
![]() $H \leq \text{G}_K$
be a closed subgroup and
$H \leq \text{G}_K$
be a closed subgroup and
![]() $L/K$
the corresponding algebraic extension. Then the maximal pro-p quotient
$L/K$
the corresponding algebraic extension. Then the maximal pro-p quotient
![]() $F := H(p) = \text{G}_L(p)$
is free pro-p [Reference Neukirch, Schmidt and WingbergNSW08, Corollary 6.1.3]. Since the quotient
$F := H(p) = \text{G}_L(p)$
is free pro-p [Reference Neukirch, Schmidt and WingbergNSW08, Corollary 6.1.3]. Since the quotient
![]() $H^{[3,p]}$
of H is pro-p, the epimorphism
$H^{[3,p]}$
of H is pro-p, the epimorphism
![]() $H \to F$
induces an isomorphism
$H \to F$
induces an isomorphism
![]() $H^{[3,p]} \cong F^{[3,p]}$
. This proves that
$H^{[3,p]} \cong F^{[3,p]}$
. This proves that
![]() $\text{G}_K$
satisfies the given condition.
$\text{G}_K$
satisfies the given condition.
Suppose conversely that K is a field of characteristic not p such that the condition on
![]() $\text{G}_K$
is satisfied; we shall show that
$\text{G}_K$
is satisfied; we shall show that
![]() $\text{Br}(K)[p] = 0$
. Let
$\text{Br}(K)[p] = 0$
. Let
![]() $L = K(\zeta_p)$
, and
$L = K(\zeta_p)$
, and
![]() $H = \text{G}_L \leq \text{G}_K$
. The group
$H = \text{G}_L \leq \text{G}_K$
. The group
![]() $G_K/H \cong \text{Gal}(L/K)$
embeds into
$G_K/H \cong \text{Gal}(L/K)$
embeds into
![]() $(\mathbb{Z}/p)^\times$
and hence is cyclic of order dividing
$(\mathbb{Z}/p)^\times$
and hence is cyclic of order dividing
![]() $p-1$
. Let F be a free pro-p group satisfying
$p-1$
. Let F be a free pro-p group satisfying
![]() $H^{[3,p]} \cong F^{[3,p]}$
. By [Reference Fried and JardenFJ08, Corollary 23.1.2] there exists a field L’ containing
$H^{[3,p]} \cong F^{[3,p]}$
. By [Reference Fried and JardenFJ08, Corollary 23.1.2] there exists a field L’ containing
![]() $\mathbb{Q}(\zeta_p)$
with absolute Galois group
$\mathbb{Q}(\zeta_p)$
with absolute Galois group
![]() $\text{G}_{L'}$
isomorphic to F. Now [Reference Chebolu, Efrat and MináčCEM12, Theorem A] implies that
$\text{G}_{L'}$
isomorphic to F. Now [Reference Chebolu, Efrat and MináčCEM12, Theorem A] implies that
![]() $H^2(\text{G}_L, \mathbb{Z}/p) \cong H^2(\text{G}_{L'}, \mathbb{Z}/p)$
, and the latter group vanishes since
$H^2(\text{G}_L, \mathbb{Z}/p) \cong H^2(\text{G}_{L'}, \mathbb{Z}/p)$
, and the latter group vanishes since
![]() $\text{G}_{L'} \cong F$
is projective. Therefore
$\text{G}_{L'} \cong F$
is projective. Therefore
![]() $H^2(\text{G}_L, \mu_p) \cong H^2(\text{G}_L, \mathbb{Z}/p)$
also vanishes. Since the restriction map
$H^2(\text{G}_L, \mu_p) \cong H^2(\text{G}_L, \mathbb{Z}/p)$
also vanishes. Since the restriction map
![]() $H^2(\text{G}_K, \mu_p) \to H^2(\text{G}_L, \mu_p)$
is injective as
$H^2(\text{G}_K, \mu_p) \to H^2(\text{G}_L, \mu_p)$
is injective as
![]() $L/K$
is of degree coprime to p,
$L/K$
is of degree coprime to p,
![]() $\text{Br}(K)[p] = H^2(\text{G}_K, \mu_p)$
must be trivial.
$\text{Br}(K)[p] = H^2(\text{G}_K, \mu_p)$
must be trivial.
Let
![]() $\mathfrak{C}$
be the class of finite groups which are extensions of an abelian group by a nilpotent group of nilpotence class at most 2. In other words,
$\mathfrak{C}$
be the class of finite groups which are extensions of an abelian group by a nilpotent group of nilpotence class at most 2. In other words,
![]() $\mathfrak{C}$
consists of finite groups G for which there exists a normal subgroup H such that
$\mathfrak{C}$
consists of finite groups G for which there exists a normal subgroup H such that
![]() $G/H$
is abelian and the quotient of H by its centre is abelian. An arbitrary profinite group G always has a maximal pro-
$G/H$
is abelian and the quotient of H by its centre is abelian. An arbitrary profinite group G always has a maximal pro-
![]() $\mathfrak{C}$
quotient
$\mathfrak{C}$
quotient
![]() $G(\mathfrak{C})$
in the usual sense [Reference Fried and JardenFJ08, Definition 17.3.2].
$G(\mathfrak{C})$
in the usual sense [Reference Fried and JardenFJ08, Definition 17.3.2].
Corollary 5.2. Let K and K’ be two fields with
![]() $\text{G}_K(\mathfrak{C}) \cong \text{G}_{K'}(\mathfrak{C})$
. If K’ has characteristic
$\text{G}_K(\mathfrak{C}) \cong \text{G}_{K'}(\mathfrak{C})$
. If K’ has characteristic
![]() $p > 0$
and
$p > 0$
and
![]() $\text{Br}(K)[p] \neq 0$
, then K also has characteristic p.
$\text{Br}(K)[p] \neq 0$
, then K also has characteristic p.
Proof. To any open normal subgroup H of
![]() $\text{G}_K$
with cyclic quotient of order dividing
$\text{G}_K$
with cyclic quotient of order dividing
![]() $p-1$
, a choice of isomorphism
$p-1$
, a choice of isomorphism
![]() $\text{G}_K(\mathfrak{C}) \cong \text{G}_{K'}(\mathfrak{C})$
associates an open normal subgroup H’ of
$\text{G}_K(\mathfrak{C}) \cong \text{G}_{K'}(\mathfrak{C})$
associates an open normal subgroup H’ of
![]() $\text{G}_{K'}$
with cyclic quotient of the same order such that the maximal two-step nilpotent quotients of H and H’ are isomorphic. In particular
$\text{G}_{K'}$
with cyclic quotient of the same order such that the maximal two-step nilpotent quotients of H and H’ are isomorphic. In particular
![]() $H^{[3,p]} \cong H'^{[3,p]}$
. Thus the lemma applies.
$H^{[3,p]} \cong H'^{[3,p]}$
. Thus the lemma applies.
We now give a sharpened version of Corollary 3.3, concerning the existence of a valuation with residue field which is not p-closed. Compared to the earlier corollary, the Galois-theoretic assumption is weakened. On the other hand, we also do not obtain full henselianity, but only p-henselianity, which was a crucial property in § 4.
Proposition 5.3. Let p be a prime,
![]() $q > 1$
a power of p, and K a field of characteristic p such that
$q > 1$
a power of p, and K a field of characteristic p such that
![]() $\text{G}_K(\mathfrak{C}) \cong \text{G}_{\mathbb{F}_q(\!(t)\!)}(\mathfrak{C})$
. Then K carries a non-trivial p-henselian valuation v whose residue field Kv is not p-closed.
$\text{G}_K(\mathfrak{C}) \cong \text{G}_{\mathbb{F}_q(\!(t)\!)}(\mathfrak{C})$
. Then K carries a non-trivial p-henselian valuation v whose residue field Kv is not p-closed.
Our proof loosely follows [Reference Efrat and FesenkoEF99, Proposition 2.3], although somewhat more work is required here. We will use the notion of l-henselianity for a valuation v on a field K, where l is an arbitrary prime number [Reference Engler and PrestelEP05, § 4.2]. So far, we have only considered this for l the characteristic of K. In general, a valuation v on K is l-henselian if it extends uniquely to every Galois extension of l-power degree, or equivalently to every
![]() $\mathbb{Z}/l$
-extension [Reference Engler and PrestelEP05, Theorem 4.2.2]. This holds if and only if Hensel’s Lemma holds for every polynomial whose roots generate a Galois extension of l-power degree [Reference Engler and PrestelEP05, Theorem 4.2.3]. If the residue field Kv is of characteristic not equal to l and K contains the lth roots of unity, this is equivalent to
$\mathbb{Z}/l$
-extension [Reference Engler and PrestelEP05, Theorem 4.2.2]. This holds if and only if Hensel’s Lemma holds for every polynomial whose roots generate a Galois extension of l-power degree [Reference Engler and PrestelEP05, Theorem 4.2.3]. If the residue field Kv is of characteristic not equal to l and K contains the lth roots of unity, this is equivalent to
![]() $1 + \mathfrak{m}_v$
being contained in the set of lth powers [Reference Engler and PrestelEP05, Corollary 4.2.4]. This is an analogue of the previously used fact that, when l is the characteristic of K, v is l-henselian if and only if
$1 + \mathfrak{m}_v$
being contained in the set of lth powers [Reference Engler and PrestelEP05, Corollary 4.2.4]. This is an analogue of the previously used fact that, when l is the characteristic of K, v is l-henselian if and only if
![]() $\mathfrak{m}_v$
is contained in the image of the polynomial
$\mathfrak{m}_v$
is contained in the image of the polynomial
![]() $X^l-X$
[Reference Chatzidakis and PereraCP17].
$X^l-X$
[Reference Chatzidakis and PereraCP17].
The following can be seen as a criterion for p-henselianity. It is inspired by the criterion for full henselianity [Reference EfratEfr95, Proposition 2.1].
Lemma 5.4. Let v be a valuation on a field K. Let l be a prime number not equal to the characteristic of Kv such that Kv is not l-closed and vK is not l-divisible. Let p also be a prime number. If v is not p-henselian, then some finite abelian extension of K has a
![]() $(\mathbb{Z}/l)^{p+1}$
-extension.
$(\mathbb{Z}/l)^{p+1}$
-extension.
Proof. There is a
![]() $\mathbb{Z}/p$
-extension
$\mathbb{Z}/p$
-extension
![]() $K'/K$
to which v does not prolong uniquely. By [Reference Engler and PrestelEP05, Theorem 3.3.3] there are precisely p prolongations
$K'/K$
to which v does not prolong uniquely. By [Reference Engler and PrestelEP05, Theorem 3.3.3] there are precisely p prolongations
![]() $w_1, \dotsc, w_p$
of
$w_1, \dotsc, w_p$
of
![]() $v|_K$
to K’, necessarily with residue field
$v|_K$
to K’, necessarily with residue field
![]() $K'w_i = Kv$
. These prolongations are incomparable [Reference Engler and PrestelEP05, Lemma 3.2.8]. Prolong each
$K'w_i = Kv$
. These prolongations are incomparable [Reference Engler and PrestelEP05, Lemma 3.2.8]. Prolong each
![]() $w_i$
as
$w_i$
as
![]() $w_i'$
to
$w_i'$
to
![]() $K'(\zeta_l)$
in some way. Noting that
$K'(\zeta_l)$
in some way. Noting that
![]() $[K'(\zeta_l) : K'] < l$
, [Reference Engler and PrestelEP05, Corollary 3.2.3] implies that each residue field
$[K'(\zeta_l) : K'] < l$
, [Reference Engler and PrestelEP05, Corollary 3.2.3] implies that each residue field
![]() $K'(\zeta_l)w_i'$
is an extension of
$K'(\zeta_l)w_i'$
is an extension of
![]() $K'w_i = Kv$
of degree less than l. Therefore none of the fields
$K'w_i = Kv$
of degree less than l. Therefore none of the fields
![]() $K'(\zeta_l)w_i'$
can be l-closed, since a
$K'(\zeta_l)w_i'$
can be l-closed, since a
![]() $\mathbb{Z}/l$
-extension of
$\mathbb{Z}/l$
-extension of
![]() $K'w_i = Kv$
cannot trivialise over
$K'w_i = Kv$
cannot trivialise over
![]() $K'(\zeta_l)w_i'$
.
$K'(\zeta_l)w_i'$
.
Let
![]() $R \subseteq K'(\zeta_l)$
be the intersection of the valuation rings
$R \subseteq K'(\zeta_l)$
be the intersection of the valuation rings
![]() $\mathcal{O}_{w_i'}$
. By [Reference Engler and PrestelEP05, Theorem 3.2.7], the natural ring homomorphism
$\mathcal{O}_{w_i'}$
. By [Reference Engler and PrestelEP05, Theorem 3.2.7], the natural ring homomorphism
![]() $R \to \prod_{i=1}^p K'(\zeta_l)w_i'$
is surjective, so in particular
$R \to \prod_{i=1}^p K'(\zeta_l)w_i'$
is surjective, so in particular
![]() $R^\times/l$
surjects onto the product of the
$R^\times/l$
surjects onto the product of the
![]() $(K'(\zeta_l)w_i')^\times/l$
. Since the fields
$(K'(\zeta_l)w_i')^\times/l$
. Since the fields
![]() $K'(\zeta_l)w_i'$
are not l-closed, Kummer theory implies that the groups
$K'(\zeta_l)w_i'$
are not l-closed, Kummer theory implies that the groups
![]() $(K'(\zeta_l)w_i')^\times/l$
are not trivial. Therefore
$(K'(\zeta_l)w_i')^\times/l$
are not trivial. Therefore
![]() $R^\times/l$
has size at least
$R^\times/l$
has size at least
![]() $l^p$
. On the other hand
$l^p$
. On the other hand
![]() $K'(\zeta_l)^\times/R^\times$
surjects onto
$K'(\zeta_l)^\times/R^\times$
surjects onto
![]() $K'(\zeta_l)^\times/\mathcal{O}_{w_1'}^\times$
, which is precisely the value group of
$K'(\zeta_l)^\times/\mathcal{O}_{w_1'}^\times$
, which is precisely the value group of
![]() $w_1'$
. This value group contains the value group of v as a subgroup of finite index, and therefore is not l-divisible since the value group of v is not l-divisible (see for instance [Reference EfratEfr06, Lemma 1.1.4(d)]). The short exact sequence
$w_1'$
. This value group contains the value group of v as a subgroup of finite index, and therefore is not l-divisible since the value group of v is not l-divisible (see for instance [Reference EfratEfr06, Lemma 1.1.4(d)]). The short exact sequence
![]() $1 \to R^\times \to K'(\zeta_l)^\times \to K'(\zeta_l)^\times/R^\times \to 1$
induces an exact sequence
$1 \to R^\times \to K'(\zeta_l)^\times \to K'(\zeta_l)^\times/R^\times \to 1$
induces an exact sequence
![]() $1 \to R^\times/l \to K'(\zeta_l)^\times/l \to (K'(\zeta_l)^\times/R^\times)/l \to 1$
since
$1 \to R^\times/l \to K'(\zeta_l)^\times/l \to (K'(\zeta_l)^\times/R^\times)/l \to 1$
since
![]() $K'(\zeta_l)^\times/R^\times$
is torsion-free. We deduce that
$K'(\zeta_l)^\times/R^\times$
is torsion-free. We deduce that
![]() $K'(\zeta_l)^\times/l$
has size at least
$K'(\zeta_l)^\times/l$
has size at least
![]() $l^{p+1}$
, and so the field
$l^{p+1}$
, and so the field
![]() $K'(\zeta_l)$
has a
$K'(\zeta_l)$
has a
![]() $(\mathbb{Z}/l)^{p+1}$
-extension by Kummer theory. The extension
$(\mathbb{Z}/l)^{p+1}$
-extension by Kummer theory. The extension
![]() $K'(\zeta_l)/K$
is abelian as the composite of the two abelian extensions
$K'(\zeta_l)/K$
is abelian as the composite of the two abelian extensions
![]() $K'/K$
and
$K'/K$
and
![]() $K(\zeta_l)/K$
.
$K(\zeta_l)/K$
.
We also require the following simple lemma for the proof of Proposition 5.3.
Lemma 5.5. Let p be a prime and
![]() $q > 1$
a power of p. There exist a prime
$q > 1$
a power of p. There exist a prime
![]() $l \neq p$
and
$l \neq p$
and
![]() $m \geq 1$
such that
$m \geq 1$
such that
![]() $l \nmid [\mathbb{F}_q : \mathbb{F}_p]$
,
$l \nmid [\mathbb{F}_q : \mathbb{F}_p]$
,
![]() $\zeta_l \not\in \mathbb{F}_q$
,
$\zeta_l \not\in \mathbb{F}_q$
,
![]() $[\mathbb{F}_p(\zeta_l) : \mathbb{F}_p]$
is a power of p, and
$[\mathbb{F}_p(\zeta_l) : \mathbb{F}_p]$
is a power of p, and
![]() $[\mathbb{F}_q(\zeta_{l^{m+1}}) : \mathbb{F}_q(\zeta_l)] = [\mathbb{F}_p(\zeta_{l^{m+1}}) : \mathbb{F}_p(\zeta_l)]$
is a power of l not equal to 1.
$[\mathbb{F}_q(\zeta_{l^{m+1}}) : \mathbb{F}_q(\zeta_l)] = [\mathbb{F}_p(\zeta_{l^{m+1}}) : \mathbb{F}_p(\zeta_l)]$
is a power of l not equal to 1.
Proof. For any natural number n, the quotient
 \[ \frac{p^{p^{n+1}}-1}{p^{p^n}-1} = \sum_{i=0}^{p-1} \big(p^{p^n}\big)^i \]
\[ \frac{p^{p^{n+1}}-1}{p^{p^n}-1} = \sum_{i=0}^{p-1} \big(p^{p^n}\big)^i \]
is congruent to p modulo
![]() $p^{p^n}-1$
, and therefore certainly coprime to
$p^{p^n}-1$
, and therefore certainly coprime to
![]() $p^{p^n}-1$
. It follows that there are infinitely many primes l dividing
$p^{p^n}-1$
. It follows that there are infinitely many primes l dividing
![]() $p^{p^n}-1$
for some n. Pick such a prime l for which
$p^{p^n}-1$
for some n. Pick such a prime l for which
![]() $l \nmid q-1$
,
$l \nmid q-1$
,
![]() $l \nmid [\mathbb{F}_q : \mathbb{F}_p]$
. We have
$l \nmid [\mathbb{F}_q : \mathbb{F}_p]$
. We have
![]() $\zeta_l \not\in \mathbb{F}_q$
since the order
$\zeta_l \not\in \mathbb{F}_q$
since the order
![]() $\lvert \mathbb{F}_q^\times\rvert = q-1$
is not a multiple of l. Let
$\lvert \mathbb{F}_q^\times\rvert = q-1$
is not a multiple of l. Let
![]() $m \geq 1$
be maximal such that
$m \geq 1$
be maximal such that
![]() $l^m \mid p^{p^n}-1$
, so that the cyclic group
$l^m \mid p^{p^n}-1$
, so that the cyclic group
![]() $\mathbb{F}_{p^{p^n}}^\times$
has elements of order
$\mathbb{F}_{p^{p^n}}^\times$
has elements of order
![]() $l^m$
, but none of order
$l^m$
, but none of order
![]() $l^{m+1}$
. This means that
$l^{m+1}$
. This means that
![]() $\zeta_l, \zeta_{l^m} \in \mathbb{F}_{p^{p^n}}$
, but
$\zeta_l, \zeta_{l^m} \in \mathbb{F}_{p^{p^n}}$
, but
![]() $\zeta_{l^{m+1}} \not\in \mathbb{F}_{p^{p^n}}$
. The degree
$\zeta_{l^{m+1}} \not\in \mathbb{F}_{p^{p^n}}$
. The degree
![]() $[\mathbb{F}_p(\zeta_l) : \mathbb{F}_p] | [\mathbb{F}_{p^{p^n}} : \mathbb{F}_p] = p^n$
is a power of p.
$[\mathbb{F}_p(\zeta_l) : \mathbb{F}_p] | [\mathbb{F}_{p^{p^n}} : \mathbb{F}_p] = p^n$
is a power of p.
The degree
![]() $[\mathbb{F}_p(\zeta_{l^{m+1}}) : \mathbb{F}_p(\zeta_l)]$
is a power of l since the extension arises as an iterated Kummer extension by successively adjoining lth roots of the element
$[\mathbb{F}_p(\zeta_{l^{m+1}}) : \mathbb{F}_p(\zeta_l)]$
is a power of l since the extension arises as an iterated Kummer extension by successively adjoining lth roots of the element
![]() $\zeta_l$
. The degree is also not 1 since
$\zeta_l$
. The degree is also not 1 since
![]() $\mathbb{F}_p(\zeta_l) \subseteq \mathbb{F}_{p^{p^n}} \not\ni \zeta_{l^{m+1}}$
. Lastly,
$\mathbb{F}_p(\zeta_l) \subseteq \mathbb{F}_{p^{p^n}} \not\ni \zeta_{l^{m+1}}$
. Lastly,
![]() $[\mathbb{F}_p(\zeta_{l^{m+1}}) : \mathbb{F}_p(\zeta_l)] = [\mathbb{F}_q(\zeta_{l^{m+1}}) : \mathbb{F}_q(\zeta_l)]$
since
$[\mathbb{F}_p(\zeta_{l^{m+1}}) : \mathbb{F}_p(\zeta_l)] = [\mathbb{F}_q(\zeta_{l^{m+1}}) : \mathbb{F}_q(\zeta_l)]$
since
![]() $\mathbb{F}_q(\zeta_l)$
and
$\mathbb{F}_q(\zeta_l)$
and
![]() $\mathbb{F}_p(\zeta_{l^{m+1}})$
are Galois extensions of
$\mathbb{F}_p(\zeta_{l^{m+1}})$
are Galois extensions of
![]() $\mathbb{F}_p(\zeta_l)$
of coprime degrees.
$\mathbb{F}_p(\zeta_l)$
of coprime degrees.
Proof of Proposition 5.3. Choose l and m as in Lemma 5.5. Fix an isomorphism
![]() $\sigma \colon \text{G}_K(\mathfrak{C}) \to \text{G}_{\mathbb{F}_q(\!(t)\!)}(\mathfrak{C})$
. Let
$\sigma \colon \text{G}_K(\mathfrak{C}) \to \text{G}_{\mathbb{F}_q(\!(t)\!)}(\mathfrak{C})$
. Let
![]() $L_0/K$
be the cyclic extension corresponding to
$L_0/K$
be the cyclic extension corresponding to
![]() $\mathbb{F}_q(\!(t)\!)(\zeta_l)/\mathbb{F}_q(\!(t)\!)$
via
$\mathbb{F}_q(\!(t)\!)(\zeta_l)/\mathbb{F}_q(\!(t)\!)$
via
![]() $\sigma$
, and let
$\sigma$
, and let
![]() $L = L_0(\zeta_l)$
. Both
$L = L_0(\zeta_l)$
. Both
![]() $L_0/K$
and
$L_0/K$
and
![]() $K(\zeta_l)/K$
are abelian extensions of p-power degree by the choice of l, and hence so is their compositum
$K(\zeta_l)/K$
are abelian extensions of p-power degree by the choice of l, and hence so is their compositum
![]() $L/K$
. Let
$L/K$
. Let
![]() $F/\mathbb{F}_q(\!(t)\!)$
be the extension corresponding to L. Since
$F/\mathbb{F}_q(\!(t)\!)$
be the extension corresponding to L. Since
![]() $L/K$
and
$L/K$
and
![]() $F/\mathbb{F}_q(\!(t)\!)$
are abelian extensions, the Galois groups
$F/\mathbb{F}_q(\!(t)\!)$
are abelian extensions, the Galois groups
![]() $\text{G}_L$
and
$\text{G}_L$
and
![]() $\text{G}_F$
have isomorphic maximal 2-step nilpotent quotients by the construction of
$\text{G}_F$
have isomorphic maximal 2-step nilpotent quotients by the construction of
![]() $\mathfrak{C}$
. In particular, the graded rings
$\mathfrak{C}$
. In particular, the graded rings
![]() $H^\ast(\text{G}_L, \mathbb{Z}/l) \cong \operatorname{K}^M_\ast(L)/l$
and
$H^\ast(\text{G}_L, \mathbb{Z}/l) \cong \operatorname{K}^M_\ast(L)/l$
and
![]() $H^\ast(\text{G}_F, \mathbb{Z}/l) \cong \operatorname{K}^M_\ast(F)/l$
are isomorphic by [Reference Chebolu, Efrat and MináčCEM12, Theorem A]. Thus
$H^\ast(\text{G}_F, \mathbb{Z}/l) \cong \operatorname{K}^M_\ast(F)/l$
are isomorphic by [Reference Chebolu, Efrat and MináčCEM12, Theorem A]. Thus
![]() $L^\times/l = \operatorname{K}^M_1(L)/l \cong F^\times/l \cong (\mathbb{Z}/l)^2$
and
$L^\times/l = \operatorname{K}^M_1(L)/l \cong F^\times/l \cong (\mathbb{Z}/l)^2$
and
![]() $\operatorname{K}^M_2(L)/l \cong H^2(\text{G}_F, \mathbb{Z}/l) = \text{Br}(F)[l] \cong \mathbb{Z}/l$
. Since the ring
$\operatorname{K}^M_2(L)/l \cong H^2(\text{G}_F, \mathbb{Z}/l) = \text{Br}(F)[l] \cong \mathbb{Z}/l$
. Since the ring
![]() $\operatorname{K}^M_\ast(L)/l$
is skew-commutative, the multiplication map
$\operatorname{K}^M_\ast(L)/l$
is skew-commutative, the multiplication map
![]() $L^\times/l \times L^\times/l \to \operatorname{K}^M_2(L)/l$
is (surjective and) skew-commutative, so
$L^\times/l \times L^\times/l \to \operatorname{K}^M_2(L)/l$
is (surjective and) skew-commutative, so
![]() $\operatorname{K}^M_2(L)/l$
is naturally identified with the second exterior power
$\operatorname{K}^M_2(L)/l$
is naturally identified with the second exterior power
![]() $\bigwedge^2_{\mathbb{F}_l} L^\times/l$
. Thus the product of any
$\bigwedge^2_{\mathbb{F}_l} L^\times/l$
. Thus the product of any
![]() $\mathbb{F}_l$
-linearly independent elements of
$\mathbb{F}_l$
-linearly independent elements of
![]() $L^\times/l$
in
$L^\times/l$
in
![]() $\operatorname{K}^M_2(L)/l$
is non-zero. Applying [Reference EfratEfr99, Main Theorem]Footnote
1
with the prime l and
$\operatorname{K}^M_2(L)/l$
is non-zero. Applying [Reference EfratEfr99, Main Theorem]Footnote
1
with the prime l and
![]() $T = L^{\times l}$
, it follows that L carries a valuation v such that
$T = L^{\times l}$
, it follows that L carries a valuation v such that
![]() $(vL : l \cdot vL) \geq l$
, the residue field Lv has characteristic not l, and
$(vL : l \cdot vL) \geq l$
, the residue field Lv has characteristic not l, and
![]() $1 + \mathfrak{m}_v \subseteq L^{\times l}$
, so (L,v) is l-henselian.
$1 + \mathfrak{m}_v \subseteq L^{\times l}$
, so (L,v) is l-henselian.
We claim that the residue field Lv does not contain
![]() $\zeta_{l^{m+1}}$
. If it does, then by l-henselianity
$\zeta_{l^{m+1}}$
. If it does, then by l-henselianity
![]() $\zeta_{l^{m+1}} \in L$
, since
$\zeta_{l^{m+1}} \in L$
, since
![]() $\zeta_{l^{m+1}}$
has l-power degree over
$\zeta_{l^{m+1}}$
has l-power degree over
![]() $L \supseteq \mathbb{F}_p(\zeta_l)$
. We know that
$L \supseteq \mathbb{F}_p(\zeta_l)$
. We know that
![]() $L^\times/l \cong (\mathbb{Z}/l)^2$
, say generated by the classes of
$L^\times/l \cong (\mathbb{Z}/l)^2$
, say generated by the classes of
![]() $a, b \in L^\times$
. Then by Kummer theory both
$a, b \in L^\times$
. Then by Kummer theory both
![]() $L(a^{1/l^{m+1}})$
and
$L(a^{1/l^{m+1}})$
and
![]() $L(b^{1/l^{m+1}})$
are
$L(b^{1/l^{m+1}})$
are
![]() $\mathbb{Z}/l^{m+1}$
-extensions of L. Their intersection is L, since their minimal non-trivial subextensions
$\mathbb{Z}/l^{m+1}$
-extensions of L. Their intersection is L, since their minimal non-trivial subextensions
![]() $L(a^{1/l})$
and
$L(a^{1/l})$
and
![]() $L(b^{1/l})$
are distinct. Therefore L has a
$L(b^{1/l})$
are distinct. Therefore L has a
![]() $(\mathbb{Z}/l^{m+1})^2$
-extension, namely
$(\mathbb{Z}/l^{m+1})^2$
-extension, namely
![]() $L(a^{1/l^{m+1}}, b^{1/l^{m+1}})$
, and accordingly F also has a
$L(a^{1/l^{m+1}}, b^{1/l^{m+1}})$
, and accordingly F also has a
![]() $(\mathbb{Z}/l^{m+1})^2$
-extension. By [Reference Neukirch, Schmidt and WingbergNSW08, Proposition 7.5.9], this implies that the residue field of F contains
$(\mathbb{Z}/l^{m+1})^2$
-extension. By [Reference Neukirch, Schmidt and WingbergNSW08, Proposition 7.5.9], this implies that the residue field of F contains
![]() $\zeta_{l^{m+1}}$
. Since
$\zeta_{l^{m+1}}$
. Since
![]() $F/\mathbb{F}_q(\!(t)\!)$
is a Galois extension of p-power degree, its residue field is a p-power degree extension of
$F/\mathbb{F}_q(\!(t)\!)$
is a Galois extension of p-power degree, its residue field is a p-power degree extension of
![]() $\mathbb{F}_q$
. However,
$\mathbb{F}_q$
. However,
![]() $\zeta_{l^{m+1}}$
has degree divisible by l over
$\zeta_{l^{m+1}}$
has degree divisible by l over
![]() $\mathbb{F}_q$
by the choice of l. This contradiction shows that
$\mathbb{F}_q$
by the choice of l. This contradiction shows that
![]() $\zeta_{l^{m+1}} \not\in Lv$
. The degree of
$\zeta_{l^{m+1}} \not\in Lv$
. The degree of
![]() $\zeta_{l^{m+1}}$
over Lv is some power of l, since
$\zeta_{l^{m+1}}$
over Lv is some power of l, since
![]() $\zeta_{l^{m+1}}$
has l-power degree over
$\zeta_{l^{m+1}}$
has l-power degree over
![]() $\mathbb{F}_p(\zeta_l) \subseteq Lv$
.
$\mathbb{F}_p(\zeta_l) \subseteq Lv$
.
We now investigate the restriction of v to K. Observe that
![]() $\zeta_{l^{m+1}}$
generates an abelian extension of Kv whose degree is divisible by l since
$\zeta_{l^{m+1}}$
generates an abelian extension of Kv whose degree is divisible by l since
![]() $\zeta_{l^{m+1}}$
has degree divisible by l even over Lv, and therefore Kv is not l-closed. If
$\zeta_{l^{m+1}}$
has degree divisible by l even over Lv, and therefore Kv is not l-closed. If
![]() $v|_K$
is not p-henselian, then by Lemma 5.4 some finite abelian extension
$v|_K$
is not p-henselian, then by Lemma 5.4 some finite abelian extension
![]() $K'/K$
has a
$K'/K$
has a
![]() $(\mathbb{Z}/l)^{p+1}$
-extension. However, the extension of
$(\mathbb{Z}/l)^{p+1}$
-extension. However, the extension of
![]() $\mathbb{F}_q(\!(t)\!)$
corresponding to it under
$\mathbb{F}_q(\!(t)\!)$
corresponding to it under
![]() $\sigma$
(as indeed any finite extension of
$\sigma$
(as indeed any finite extension of
![]() $\mathbb{F}_q(\!(t)\!)$
) does not have a
$\mathbb{F}_q(\!(t)\!)$
) does not have a
![]() $(\mathbb{Z}/l)^{p+1}$
-extension [Reference Neukirch, Schmidt and WingbergNSW08, Proposition 7.5.9]. This contradiction shows the p-henselianity of
$(\mathbb{Z}/l)^{p+1}$
-extension [Reference Neukirch, Schmidt and WingbergNSW08, Proposition 7.5.9]. This contradiction shows the p-henselianity of
![]() $v|_K$
.
$v|_K$
.
Lastly, let us show that
![]() $\zeta_l \not\in Kv$
. Suppose for a contradiction that
$\zeta_l \not\in Kv$
. Suppose for a contradiction that
![]() $\zeta_l \in Kv$
, then also
$\zeta_l \in Kv$
, then also
![]() $\zeta_l \in K$
as
$\zeta_l \in K$
as
![]() $\zeta_l$
has p-power degree over
$\zeta_l$
has p-power degree over
![]() $\mathbb{F}_p$
and
$\mathbb{F}_p$
and
![]() $v|_K$
is p-henselian. Therefore K has a
$v|_K$
is p-henselian. Therefore K has a
![]() $(\mathbb{Z}/l)^2$
-extension, given by on the one hand adjoining an lth root of an element
$(\mathbb{Z}/l)^2$
-extension, given by on the one hand adjoining an lth root of an element
![]() $x \in K^\times$
with
$x \in K^\times$
with
![]() $v(x) \in vK$
not divisible by l, and on the other hand adjoining an lth power root of unity (since we know that
$v(x) \in vK$
not divisible by l, and on the other hand adjoining an lth power root of unity (since we know that
![]() $\zeta_{l^{m+1}}$
does not lie in Lv and therefore not in K). However,
$\zeta_{l^{m+1}}$
does not lie in Lv and therefore not in K). However,
![]() $\mathbb{F}_q(\!(t)\!)$
does not have a
$\mathbb{F}_q(\!(t)\!)$
does not have a
![]() $(\mathbb{Z}/l)^2$
-extension, so given the isomorphism
$(\mathbb{Z}/l)^2$
-extension, so given the isomorphism
![]() $\sigma$
we once more obtain a contradiction. Therefore
$\sigma$
we once more obtain a contradiction. Therefore
![]() $Kv(\zeta_l)/Kv$
is a non-trivial Galois extension which is of p-power degree by the choice of l. Thus Kv is not p-closed.
$Kv(\zeta_l)/Kv$
is a non-trivial Galois extension which is of p-power degree by the choice of l. Thus Kv is not p-closed.
Remark 5.6. Inspection of the proof shows that the valuation v is not only p-henselian, but in fact r-henselian for every prime number r, since Lemma 5.4 can be applied for primes other than the characteristic p.
We can now deduce the following strengthened version of Theorem 1.1.
Theorem 5.7. Let p be a prime number,
![]() $q = p^n$
for some
$q = p^n$
for some
![]() $n \geq 1$
. Let K be a field satisfying the following axioms:
$n \geq 1$
. Let K be a field satisfying the following axioms:
-
(Gal0) the maximal pro-
 $\mathfrak{C}$
quotients
$\mathfrak{C}$
quotients
 $\text{G}_K(\mathfrak{C})$
and
$\text{G}_K(\mathfrak{C})$
and
 $\text{G}_{\mathbb{F}_q(\!(t)\!)}(\mathfrak{C})$
are isomorphic, where
$\text{G}_{\mathbb{F}_q(\!(t)\!)}(\mathfrak{C})$
are isomorphic, where
 $\mathfrak{C}$
is (as above) the class of finite groups which are extensions of an abelian group by a nilpotent group of nilpotence class at most 2;
$\mathfrak{C}$
is (as above) the class of finite groups which are extensions of an abelian group by a nilpotent group of nilpotence class at most 2; -
(Imp) K has exponent of imperfection at most 1;
-
(Brau)
 $\text{Br}(K)[p] \cong \mathbb{Z}/p\mathbb{Z}$
; and
$\text{Br}(K)[p] \cong \mathbb{Z}/p\mathbb{Z}$
; and -
(Pair) the natural pairing
 $\text{Hom}(\text{G}_K, \mathbb{Z}/p) \times K^\times/p \to \text{Br}(K)[p]$
induces an isomorphism
$\text{Hom}(\text{G}_K, \mathbb{Z}/p) \times K^\times/p \to \text{Br}(K)[p]$
induces an isomorphism
 $K^\times/p \cong \text{Hom}(\text{Hom}(\text{G}_K, \mathbb{Z}/p), \text{Br}(K)[p])$
.
$K^\times/p \cong \text{Hom}(\text{Hom}(\text{G}_K, \mathbb{Z}/p), \text{Br}(K)[p])$
.
Then K is isomorphic to the local field
![]() $\mathbb{F}_q(\!(t)\!)$
.
$\mathbb{F}_q(\!(t)\!)$
.
Proof. By Corollary 5.2, K has characteristic p. By Proposition 5.3, K carries a non-trivial p-henselian valuation v whose residue field is not p-closed. Now Proposition 4.7 shows that K is isomorphic to
![]() $\mathbb{F}_{q'}(\!(t)\!)$
for some power q’ of p. If we had
$\mathbb{F}_{q'}(\!(t)\!)$
for some power q’ of p. If we had
![]() $q' \neq q$
, then
$q' \neq q$
, then
![]() $\text{G}_{\mathbb{F}_{q'}(\!(t)\!)}^{\mathrm{ab}} \not\cong \text{G}_{\mathbb{F}_q(\!(t)\!)}^{\mathrm{ab}}$
by [Reference Neukirch, Schmidt and WingbergNSW08, Proposition 7.5.9], and so in particular
$\text{G}_{\mathbb{F}_{q'}(\!(t)\!)}^{\mathrm{ab}} \not\cong \text{G}_{\mathbb{F}_q(\!(t)\!)}^{\mathrm{ab}}$
by [Reference Neukirch, Schmidt and WingbergNSW08, Proposition 7.5.9], and so in particular
![]() $\text{G}_{\mathbb{F}_{q'}(\!(t)\!)}(\mathfrak{C}) \not\cong \text{G}_{\mathbb{F}_q(\!(t)\!)}(\mathfrak{C})$
. Therefore
$\text{G}_{\mathbb{F}_{q'}(\!(t)\!)}(\mathfrak{C}) \not\cong \text{G}_{\mathbb{F}_q(\!(t)\!)}(\mathfrak{C})$
. Therefore
![]() $q' = q$
and
$q' = q$
and
![]() $K \cong \mathbb{F}_q(\!(t)\!)$
.
$K \cong \mathbb{F}_q(\!(t)\!)$
.
The choice of the class of groups
![]() $\mathfrak{C}$
is not quite optimal. It is already apparent from the proofs above that it could be shrunk by some amount, strengthening the statement of Theorem 5.7. However, this would yield a class less easy to describe than
$\mathfrak{C}$
is not quite optimal. It is already apparent from the proofs above that it could be shrunk by some amount, strengthening the statement of Theorem 5.7. However, this would yield a class less easy to describe than
![]() $\mathfrak{C}$
.
$\mathfrak{C}$
.
Acknowledgements
I would like to thank the anonymous referee for a very careful reading of the manuscript and a number of helpful suggestions, which helped improve the presentation.
Conflicts of interest
None.
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.