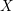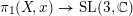Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Langer, Adrian
2021.
On Smooth Projective D-Affine Varieties.
International Mathematics Research Notices,
Vol. 2021,
Issue. 15,
p.
11889.
Budur, Nero
Lerer, Leonardo A.
and
Wang, Haopeng
2023.
Absolute sets of rigid local systems.
Annales de l'Institut Fourier,
Vol. 73,
Issue. 2,
p.
829.
He, Siqi
and
Liu, Jie
2024.
On the spectral variety for rank two Higgs bundles.
Proceedings of the London Mathematical Society,
Vol. 129,
Issue. 5,
Langer, Adrian
2024.
On algebraic Chern classes of flat vector bundles.
manuscripta mathematica,
Vol. 174,
Issue. 1-2,
p.
1.