Hostname: page-component-7dd5485656-zklqj Total loading time: 0 Render date: 2025-10-31T15:27:59.406Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectre et géométrie conforme des variétés compactes à bord

Part of: Partial differential equations on manifolds; differential operators Spectral theory and eigenvalue problems

Published online by Cambridge University Press:  28 October 2014

Pierre Jammes
Pierre Jammes*
Affiliation:
Laboratoire J.-A. Dieudonné, Université Nice Sophia Antipolis — CNRS (UMR 7351), Parc Valrose, 06108 Nice Cedex 02, France email pjammes@unice.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that on any compact manifold 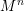$M^{n}$ with boundary, there exists a conformal class 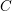$C$ such that for any Riemannian metric 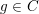$g\in C$ of unit volume, the first positive eigenvalue of the Neumann Laplacian satisfies 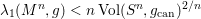${\it\lambda}_{1}(M^{n},g)<n\,\text{Vol}(S^{n},g_{\text{can}})^{2/n}$. We also prove a similar inequality for the first positive Steklov eigenvalue. The proof relies on a handle decomposition of the manifold. We also prove that the conformal volume of 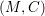$(M,C)$ is 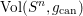$\text{Vol}(S^{n},g_{\text{can}})$, and that the Friedlander–Nadirashvili invariant and the Möbius volume of 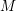$M$ are equal to those of the sphere. If 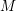$M$ is a domain in a space form, 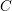$C$ is the conformal class of the canonical metric.

Keywords

first Neumann and Steklov eigenvalueconformal volume

MSC classification

Primary: 35P15: Estimation of eigenvalues, upper and lower bounds 58J50: Spectral problems; spectral geometry; scattering theory

Information

Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 12 , December 2014 , pp. 2112 - 2126
Copyright
© The Author 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ashbaugh, M. and Benguria, R., Sharp upper bound to the first nonzero Neumann eigenvalue for bounded domains in spaces of constant curvature, J. Lond. Math. Soc. (2) 52 (1995), 402–416.Google Scholar
Ammann, B. and Bär, C., Dirac eigenvalues and total scalar curvature, J. Geom. Phys. 33 (2000), 229–234.Google Scholar
Ammann, B. and Jammes, P., The supremum of first eigenvalues of conformally covariant operators in a conformal class, in Variational problems in differential geometry, London Mathematical Society Lecture Note Series, vol. 394 (Cambridge University Press, Cambridge, 2012), 1–23.Google Scholar
Bandle, C., Isoperimetric inequalities and applications, Monographs and Studies in Mathematics, vol. 7 (Pitman, London, 1980).Google Scholar
Beardon, A., The geometry of discrete groups (Springer, New York, 1983).CrossRefGoogle Scholar
Brooks, R. and Makover, E., Riemann surfaces with large first eigenvalue, J. Anal. Math. 83 (2001), 243–258.CrossRefGoogle Scholar
Buser, P., On the bipartition of graphs, Discrete Appl. Math. 9 (1984), 105–109.CrossRefGoogle Scholar
Colbois, B. and Dodziuk, J., Riemannian metrics with large 𝜆1, Proc. Amer. Math. Soc. 122 (1994), 905–906.Google Scholar
Colbois, B. and El Soufi, A., Extremal eigenvalues of the Laplacian in a conformal class of metrics : the ‘conformal spectrum’, Ann. Global Anal. Geom. 23 (2003), 337–349.Google Scholar
Colbois, B. and El Soufi, A., Eigenvalues of the Laplacian acting on p-forms and metric conformal deformations, Proc. Amer. Math. Soc. 134 (2006), 715–721.Google Scholar
Colbois, B., El Soufi, A. and Girouard, A., Isoperimetric control of the Steklov spectrum, J. Funct. Anal. 261 (2011), 1384–1399.Google Scholar
Dodziuk, J., Eigenvalues of the Laplacian on forms, Proc. Amer. Math. Soc. 85 (1982), 438–443.Google Scholar
El Soufi, A., Giacomini, H. and Jazar, M., A unique extremal metric for the least eigenvalue of the Laplacian on the Klein bottle, Duke Math. J. 135 (2006), 181–202.Google Scholar
El Soufi, A. and Ilias, S., Immersions minimales, première valeur propre du laplacien et volume conforme, Math. Ann. 275 (1986), 257–267.CrossRefGoogle Scholar
El Soufi, A. and Ilias, S., Majoration de la seconde valeur propre d’un opérateur de Schrödinger sur une variété compacte et applications, J. Funct. Anal. 103 (1992), 294–316.CrossRefGoogle Scholar
Friedlander, L. and Nadirashvili, N., A differential invariant related to the first eigenvalue of the Laplacian, Int. Math. Res. Not. IMRN 17 (1999), 939–952.Google Scholar
Fraser, A. and Schoen, R., The first Steklov eigenvalue, conformal geometry, and minimal surfaces, Adv. Math. 226 (2011), 4011–4030.Google Scholar
Girouard, A., Fundamental tone, concentration of density to points and conformal degeneration on surfaces, Canad. J. Math. 61 (2009), 548–565.Google Scholar
Gentile, G. and Pagliara, V., Riemannian metrics with large first eigenvalue on forms of degree p, Proc. Amer. Math. Soc. 123 (1995), 3855–3858.Google Scholar
Hassannezhad, A., Conformal upper bounds for the eigenvalues of the Laplacian and Steklov problem, J. Funct. Anal. 261 (2011), 3419–3436.Google Scholar
Hersch, J., Quatre propriétés isopérimétriques de membranes sphériques homogènes, C. R. Acad. Sci. Paris Sér. A–B 270 (1970), A1645–A1648.Google Scholar
Hirsch, M. W., Differential topology, Graduate Texts in Mathematics, vol. 33 (Springer, 1994).Google Scholar
Jammes, P., Première valeur propre du laplacien, volume conforme et chirurgies, Geom. Dedicata 135 (2008), 29–37.Google Scholar
Jakobson, D., Levitin, M., Nadirashvili, N., Nigam, N. and Polterovich, I., How large can the first eigenvalue be on a surface of genus two?, Int. Math. Res. Not. IMRN 63 (2005), 3967–3985.Google Scholar
Jakobson, D., Nadirashvili, N. and Polterovich, I., Extremal metric for the first eigenvalue on a Klein bottle, Canad. J. Math. 58 (2006), 381–400.Google Scholar
Kokarev, G. and Nadirashvili, N., On first Neumann eigenvalue bounds for conformal metrics, Around the research of Vladimir Maz’ya. II, International Mathematics Series (NY), vol. 12 (Springer, New York, 2010), 229–238.Google Scholar
Kosinski, A., Differential manifolds (Academic Press, New York, 1993).Google Scholar
Li, P. and Yau, S.T., A new conformal invariant and its applications to the Willmore conjecture and the first eigenvalue of compact surfaces, Invent. Math. 69 (1982), 269–291.CrossRefGoogle Scholar
McGowan, J., The p-spectrum of the Laplacian on compact hyperbolic three manifolds, Math. Ann. 297 (1993), 725–745.CrossRefGoogle Scholar
Mutô, H., The first eigenvalue of the Laplacian on even-dimensional spheres, Tôhoku Math. J. (2) 32 (1980), 427–432.Google Scholar
Nadirashvili, N., Berger’s isoperimetric problem and minimal immersions of surfaces, Geom. Funct. Anal. 6 (1996), 877–897.CrossRefGoogle Scholar
Petrides, R., On a rigidity result for the first conformal eigenvalue of the Laplacian, prépublication (2013), arXiv:1310.4698.Google Scholar
Petrides, R., Existence and regularity of maximal metrics for the first Laplace eigenvalue on surfaces, Geom. Funct. Anal. 24 (2014), 1336–1376.Google Scholar
Ranicki, A., Algebraic and geometric surgery (Oxford University Press, Oxford, 2002).Google Scholar
Stekloff, W., Sur l’existence des fonctions fondamentales, C. R. Acad. Sci. Paris 128 (1899), 808–810.Google Scholar
Stekloff, W., Sur les problèmes fondamentaux de la physique mathématique (suite et fin), Ann. Sci. Éc. Norm. Supér. (3) 19 (1902), 455–490.CrossRefGoogle Scholar
Tanno, S., The first eigenvalue of the Laplacian on spheres, Tôhoku Math. J. (2) 31 (1979), 179–185.CrossRefGoogle Scholar
Weinstock, R., Inequalities for a classical eigenvalue problem, J. Ration. Mech. Anal. 3 (1954), 745–753.Google Scholar