A contractualist approach to threshold deontology: the case of ex-post regulatory changes

Abstract

Common sense morality follows – in many cases – the prescriptions of threshold deontology. Governments, for example, are expected to follow their own rules, but in the face of an extreme price increase, public opinion has often supported changing the rules ex post to increase tax revenues. Such moral license in extreme situations is puzzling from a philosophical and an economic point of view. We present a simple contractualist solution to this puzzle using a game-theoretic model. We argue that allowing for deviations from the social contract in extreme circumstances is a necessary condition for the stability of any social contract.

1. Introduction

In the past two decades, mainly during 2000–2010 following significant developments in the oil and gas industries that led to major price changes, many western governments made ex post regulatory changes so as to increase their tax revenues. These changes often gave rise to heated public controversies and, in some cases, led the companies concerned to pursue legal action against those governments. Between 2001 and 2010 the number of arbitration cases for oil and gas were around 10 times greater than they had been during the previous decade (Mansour and Nakhle 2016).

While this phenomenon raises several interesting questions from a descriptive point of view, it also constitutes a real-world example – one with significant implications for public policy – of a well-known normative puzzle, namely the puzzle of threshold deontology.

The puzzle is as follows. Although common sense morality demands performing (or refraining from performing) certain actions even though an alternative course of action is superior from a purely consequentialist perspective, in some cases the demand to act this way becomes highly unintuitive when the stakes are high enough (i.e. when enough added value can be gained). However, there seems to be no non-arbitrary way to fix the threshold above which the consequentialist consideration becomes dominant. For instance, although most people judge killing one person in order to save the lives of two other people impermissible, they may judge killing one person in order to save the lives of a thousand people permissible or even mandatory. This raises the question as to where exactly the threshold for permissible killing ought to be set, and there seems to be no non-arbitrary way to answer it.

The puzzle manifests itself in the context of ex post regulatory changes: we usually expect governments to respect their commitments, even when by breaking them they could actually serve the public interest. On the other hand, in extreme cases where enough revenue can be gained by breaking a given commitment, we tend to criticize governments for not doing so. However, in the absence of an account of how to set the threshold above which ex post regulatory changes are permissible this pattern of judgements seems hard to justify.

In this paper we offer a solution to this normative puzzle. Our discussion focuses on the case of ex post regulatory changes, which is of imminent importance for public policy, as an example, but, as will become clear, can easily be extended to other contexts in which the puzzle arises (albeit possibly not to all such contexts). ¹ The solution takes the form of a moral justification for the pattern of judgements described above and an explanation for how the threshold is set in a non-arbitrary way. Although we believe that it may be possible to translate the argument from the moral domain to the legal domain and that it might also be possible to formulate it as an explanation for governments’ behaviour, we limit our attention to the moral question.

Our argument is formulated in, and is inspired by, the general normative-conceptual framework suggested by Ken Binmore (for example in his 1989, 1991, 2005 and 2010 studies). ² Specifically, it is based on two main assumptions:

1. (a) We assume a somewhat limited commitment (as explained in section 3) to a social contract approach with respect to some social norms.

2. (b) We assume that a necessary (but not sufficient) condition for a given social norm being part of the social contract is that it is supported by an equilibrium (subgame-perfect Nash) in the infinitely repeated game that captures the relevant social dynamic.

We do not aim to justify these two assumptions. However, we believe that, by showing how in relying on them we achieve a solution to the threshold deontology puzzle, we provide an indirect argument for them.

We use a game-theoretic model of an infinitely repeated game with chance moves that describes the interaction between different agents in a given society. In our example, the relevant agents are the government, on the one hand, and the oil and gas companies, on the other. It is shown that under certain conditions, which it is natural to assume hold in the relevant class of cases, there cannot exist a stable social contract (i.e. one that is supported by a subgame-perfect Nash equilibrium) in which the government never breaks its commitments. However, there can be an equilibrium in which the government deviates from its commitments in extreme situations but respects them in all other cases. Importantly, in such an equilibrium, the other player (which represents the private sector) cooperates both before and after the government’s deviation. Thus, our account applies not only to deontological justifications for the demand that governments keep their commitments; it also applies to consequentialist justifications, which usually concentrate on the advantages in the long run of regulatory stability and of trust between the government and the private sector.

On an intuitive level, the argument is that it is permissible for governments to break their explicit promises when the stakes are high because these promises were originally understood (or could only be understood by any rational player) as including an implicit qualification for non-extreme cases. Without such a qualification it would be irrational for the government to make the commitment in the first place.

According to our account, what qualifies as an “extreme case” (or what determines where the threshold is set) is endogenously constrained by the strategic considerations of both the government and the private sector. Specifically, the threshold is constrained by the utilities and uncertainty that the players face and the discount factor that the government uses when considering the long run. ³

As noted above, a similar strategy may be employed in other cases (but probably not in all cases) in which the threshold deontology puzzle arises. To the extent that the relevant normative rule (the one that intuitively should be respected as long as respecting it does not cost too much in consequentialist terms) can be seen as supported by a subgame-perfect Nash equilibrium in an infinitely repeated game with chance moves that describe the relevant social dynamic, a justification for threshold deontology, along similar lines, can probably be presented, Of course, the specific game we use to model the interaction between the relevant agents in our example cannot capture all social interactions that might lead to the emergence of threshold deontology social norms. However, the main argumentative move can be easily replicated in the context of other types of social dynamics.

The remainder of the paper is organized as follows:

1. – In section 2 we cover some background necessary for understanding our example. We explain the importance of regulatory stability and present evidence for the existence and scale of the phenomenon of ex-post regulatory changes.

2. – In section 3 we present the normative puzzle we aim to solve and explain how our model constitutes a solution to it.

3. – In section 4 we present the model itself, state the mathematical propositions needed for our argument to apply, and explain in a semi-formal way the model’s proof. We also demonstrate how our account can lead to the recommendation to adopt specific policy tools in cases where the government has the ability to influence market norms.

4. – Section 5 concludes.

The formal proofs are set out in the Appendix.

2. Deviations from Equilibrium and Threshold Deontology in Public Policy

Over the past two decades, as fiscal policy and budget deficits became more pressing issues in many well-developed countries and public discussion of questions regarding tax equality became more prominent, many governments began putting significant effort into increasing the public benefits from natural resources. As a result, regulatory stability in the context of natural resources has been repeatedly challenged. These changes typically occur when an exogenous shock causes a dramatic change in the public sector’s share in profits. When a strong deviation occurs from what the government or the public perceive as a ‘fair’ share of benefits, we can expect to see a major change in regulation. These changes are sometimes enacted retroactively – with emphasis on existing projects, which determine the government’s monetary gains in the short term.

According to Stevens et al. (2013), more than 30 countries revised their petroleum contracts or entire fiscal regimes between 2000 and 2010, a period that witnessed major oil prices changes (from $20 a barrel in 1999 to more than $100 in 2008, inflation-adjusted). All around the world, ‘the rules of the game’ in the oil and gas sector changed. Pursuing their own initiative in some cases and following public pressure in others, governments found legislative justifications to make major adjustments to raise the public share. The change in prices shifted the global power balance away from companies to host governments and the risk of unilateral action by host governments remains as significant for investors today as ever (Cameron 2016). Figure 1 describes the policy changes and the increase in the government take.

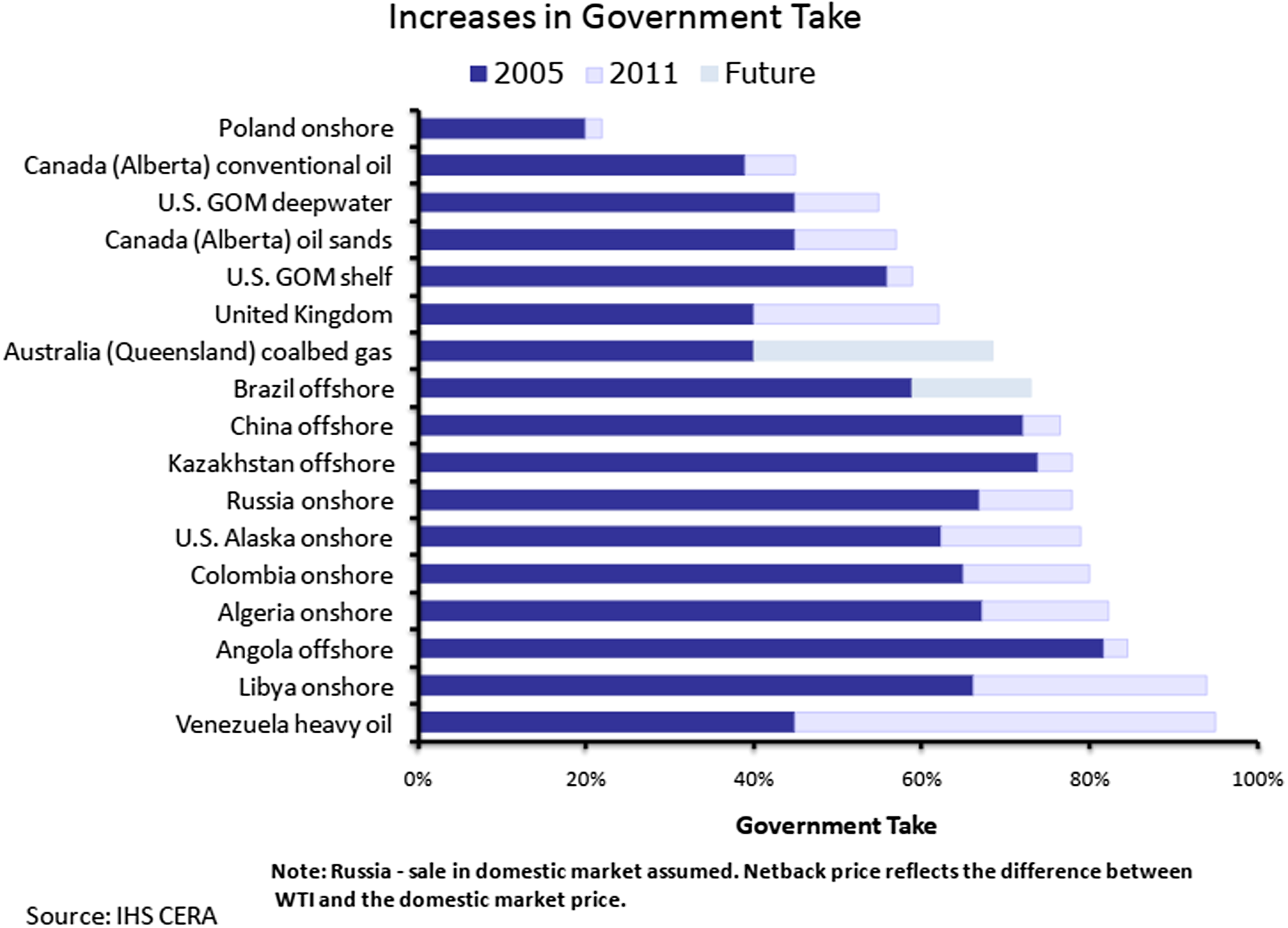
Figure 1. Increases in Government take 2005–2011.

The public discussion surrounding the fiscal regime changes around the world has focused on whether retroactive tax changes (i.e. changing the rules of the game while the game is being played) are justified, given the extreme market price changes and the dramatic decline in government share in the oil and gas sector. Although these acts were accompanied by public and legal struggles, in many developed countries changes in the fiscal regime in the oil and gas sector were made with an eye on existing projects. The public debate raised the importance of investors’ trust in the fiscal regimes’ stability. To maintain this trust, it is crucial to understand whether the governmental action is to be perceived as part of an equilibrium, or a deviation from it.

A short discussion of two examples of changing the fiscal regime in the oil and gas sector can shed light on the dynamics of the perceived equilibrium between the government (representing the public share) and the private sector. In 2006, the UK government increased the supplementary charge tax (SCT) from 10% to 20% and then to 32%. The declared objective of this change was “to obtain a fair share of the net income from these resources for the nation, primarily through taxation” (HM Treasury 2014). When oil prices increased sharply and the perception of a fair government share eroded, the equilibrium became unstable and the change occurred.

The changes in the fiscal regulation of the natural gas sector in Israel in the past decade are another example of changing the rules during the game in extreme cases. Following more than half a century of minor natural gas reservoir discoveries, a relatively big and profitable reservoir was discovered in 2009. In 2010 a government committee (the Sheshinski Committee) recommended a completely new fiscal regime in order to balance the fair profits of the private partnership (local and international companies) and the government’s revenues (Sheshinski 2011). ⁴ After a long public hearing, legislation was enacted that more than doubled the total government take.

Nobel laureate in economics Robert Aumann publicly objected to the so-called “retroactive change”, stating in an interview: “You can’t change the rules during the game. When you do so, you don’t signal the right incentive. It damages trust in the system and it is not moral” (Aumann 2011). As Aumann’s statement demonstrates, the practice of ex post regulatory changes raises two related but distinct objections. First, it is argued that this practice is inefficient in the long run (even if leading to sharp increases in government revenues in the short term). Second, it is argued that, irrespective of the question of efficiency, it is unfair.

As we explain in the next section, our proposed solution answers both of these objections (in the type of cases to which it applies).

However, clearly Aumann had a point. The importance of securing property rights and protecting the accumulation of wealth for economic growth is widely discussed in the literature. Economists since Montesquieu (1748) and Adam Smith (1776) have identified the protection of property rights as essential for growth and prosperity. These basic principles have always shaped the evolution of social institutions. For economic growth to occur the sovereign or government must not merely establish the relevant set of rights, but must also make a credible commitment to them. The ability of a government to commit to private rights is thus an essential condition for economic growth. Credible commitment by the government to honour its financial agreements is part of the larger commitment to securing property rights. The likelier it is that the sovereign will alter property rights for its own benefit, the lower the expected returns from investment and hence the lower the incentive to invest (North and Weingast 1989).

Thus, many governments perceive fiscal stability as a foundation stone of the tax system. Governments try to signal stability in regulation related to property rights and wealth accumulation. Changes in tax regulations, when they occur, are widely made on a gradual basis to signal tax stability and thereby not deter investors.

Yet, as we can see even in well-developed countries, extreme cases (i.e. where the stakes are high enough) often lead to major changes.

The investors and the business sector players (especially large international firms) cope with a deviation from the existing equilibrium in several ways, but in many cases, after failed attempts to influence the new regulation, they tend to accept the changes in fiscal regulation, and continue their activity, including making new investments.

A good example is ExxonMobil (a large oil company) which, like many other oil companies, includes in its yearly financial report the following statement: “Regulatory and litigation risks: Even in countries with well-developed legal systems where ExxonMobil does business, we remain exposed to changes in law (including changes that result from international treaties and accords) that could adversely affect our results, such as increase in taxes or government royalty rates (including retroactive claims)” (ExxonMobil 2009).

Similarly, in the Israeli case, the private companies tried unsuccessfully to fight the government’s move both in the political and the public arenas but eventually accepted the changes. As the local CEO of Noble Energy stated in an interview: “After the Sheshinski [Committee’s] recommendations, we clarified that we accept the ruling” (Zomer 2015). This acceptance was realized by refraining from initiating arbitration procedures in the international arbitration court, completing the investment, and even entering a new large investment project.

The important question from a public policy perspective is, of course, which exogenous shocks justify, a deviation from an existing fiscal regime. Surely, not all shocks do that. Below we try to shed light on this question, by adopting a contractualist approach and representing the dynamic between governments and oil and gas companies in a game-theoretic model.

3. A Contractualist Approach to Threshold Deontology

The phenomenon described in the previous section, i.e. the sharp increase in the number and extent of retroactive changes in the regulation of the oil and gas industries, constitutes not only a challenge for regulators but also an instance of a general normative puzzle, namely the puzzle of threshold deontology (for some discussions see Alexander 2000; Smilansky 2003; Zamir and Medina 2008, 2011; Cook 2017; Rosenthal 2018; Johnson 2020).

According to threshold deontology, there are some normative principles that must be respected even when doing so leads to outcomes that are overall worse than the outcomes that could have been achieved by violating the principles. However, this demand is limited to cases in which the overall loss (in terms of whatever benefits are at stake) is not extreme. Despite threshold deontology being very intuitive, it is usually taken to be hard to defend. The main problem associated with it is that there seems to be no non-arbitrary ways to fix the threshold above which violations of a given deontological principle are required (or even merely permissible). This problem can easily be translated into several counterintuitive examples (see, for example, Alexander 2000). Here we suggest a non-arbitrary way to determine the threshold in the context of the phenomenon described in the previous section.

As our starting point we assume that it is generally a bad thing for governments not to keep their promises, even if by doing so they can increase overall social welfare. While this assumption can plausibly be taken to be deontological in nature, one can also accept it on purely consequentialist grounds. As explained in the previous section, the most straightforward way to do so (adopted by most economists writing on the subject) is to argue that, while it is always the state’s obligation to maximize social welfare, governments typically have a reason to keep their promises because such a policy is the most efficient in the long run.

For those who adopt such a purely consequentialist position, the normative challenge presented above (i.e. finding a non-arbitrary way to determine the threshold) changes its nature, but still holds. The problem, from a purely consequentialist point of view, is not the arbitrariness of the threshold, as according to such an approach the threshold is determined in a straightforward utilitarian way. It’s rather that the way the threshold is determined seems to be sensitive to the wrong types of variables.

First, there seem to be many cases in which a government can easily increase social welfare by violating basic rights, while hiding its wrongdoings. Thus, the government prevents the bad consequentialist side effects of the basic rights violations. Still, in these cases we intuitively judge the violation of rights to be morally wrong. Second, and more importantly for our purposes here, the social-welfare-maximization-in-the-long-term approach does not distinguish between cases that involve the same expected payoffs with different probability distributions over possible prizes.

Compare:

A. An investor who makes a low-risk investment with an expected value of W (say, the probability of winning W+a is equal to the probability of winning W−a, both being 0.5).

B. An investor who makes a high-risk investment with the same expected payoff (say, the probability of winning W+1000a is equal to the probability of winning W−1000a, both being 0.5).

On the face of it, both types of investment enjoy the same expected payoff and thus the damage to future investments done by the government changing taxation laws regarding these two types of investment are equal.

Moreover, if, as governments often do (as seen in section 1), the government changes taxation laws only in cases of type B but not in cases of type A, the investor in cases of type B can justifiably (so it seems) complain of unequal treatment. This is because she and the type-A investor face the same expected payoff.

We suggest that from a contractualist point of view, these two cases are different in an important sense. Thus, our suggestion solves the normative puzzle both for threshold deontologists and for pure consequentialists.

As noted in the Introduction, our approach is inspired by the general conceptual-normative contractualist framework suggested by Ken Binmore for understating justice norms. However, our commitment to contractualism is quite limited (much more so than Binmore’s, we suspect). In order to articulate this commitment and to locate it in the relevant literature, it will be useful to use Shelly Kagan’s (1992) distinction between factorial and foundational moral inquiry (which Zamir and Medina (2011) also utilize in their influential discussion of threshold deontology). ⁵

A factorial moral inquiry aims to identify the different moral factors operating in a given context (i.e. the variables that determine the overall moral status of the possible acts available to the moral agent in a context of choice). It also aims at explaining how these factors interact and to identify the mechanisms through which their interaction determines the overall moral status of the possible acts available for choice.

A foundational moral inquiry aims to explain what makes these factors the relevant moral factors and – similarly – what makes the mechanisms through which they interact, the mechanism that determines the overall moral status of the possible acts.

Kagan (1992: 225) mentions contractualism as an example of a foundational moral theory (or a group of foundational moral theories). Roughly it is the theory according to which what makes a feature of the world a moral factor is the agreement of rational agents to let it play a certain action-guiding role. Zamir and Medina (2011) take threshold deontology to be an example of a group of factorial moral theories. Roughly it is the group of theories according to which obeying certain rules is one moral factor, advancing some consequentialist value is another moral factor, and these factors interact in the following way: an act is mandatory iff it either 1. dictated by one of the rules and choosing it does not lead to a loss of the consequentialist value, greater than a given threshold or 2. It prevents a loss of the consequentialist value, greater than the given threshold.

Both Kagan and Zamir and Medina emphasise that a given theoretical commitment on the factorial level can be supported by different theoretical commitments on the foundational level. However, Kagan also recognizes that “Ideally, an adequate foundational theory would … illuminate how the various factors interact in determining the moral status of an act, explaining which factors outweigh the others in cases of conflict, and why” (Kagan 1992: 226). Although this ideal is almost never fully satisfied by actual foundational moral theories, surely, the ability of a foundational moral theory (or of a theoretical commitment on the foundational level) to predict and explain intuitive claims about the factorial level is an advantage. This is so both epistemically and practically. Epistemically, it is an indication that the theory (or the theoretical commitment) is true. Practically, it enables the theory to be action-guiding (or, at least, to shed light on what the theory’s prescriptions in actual cases are).

This is exactly the case, we believe, when it comes to our claims here. Our suggestion works on the foundational level (although it falls short of being a complete foundational theory), but it vindicates the factorial commitments of threshold deontology, which are highly intuitive. Moreover, and as we demonstrate in the next two next sections, it also sheds light on the question as to which variables determine the threshold and how, thus supplying general guidelines for applying the theory in actual cases.

As noted, we do not need to assume that the normative foundations of all moral factors are contractualist in nature. Some moral factors – such as the moral rule according to which one ought not physically harm another human being for mere pleasure – might be true independently of the existence of an implicit contract among the members of society.

Similarly, we do not need to deny that the normative significance of some consequentialist values is independent of an underlying social contract. For example, we do not need to deny that increasing well-being is good in itself.

In other words, in order to support our account it is enough to adopt a pluralist approach on the foundational level (i.e. one according to which, deontological, consequentialist, contractualist and other principles play a foundational role) with only a minimal commitment to contractualism (however, of course, everything we say in the paper is consistent with a fully contractualist foundational moral theory. It is just that we do not have to make such a strong commitment on the foundational level, in order for our claims in the paper to go through).

Our commitment to contractualism, on the foundational level, can be limited to cases of two types. First, in some cases people face decision problems in which, no matter how they choose, there will be a violation of at least one moral rule (that operates on the foundational level). Second, in some cases in which in order to choose the way that best serves a given consequentialist value (e.g. maximizing social welfare) people must make interpersonal comparisons of the given value and, in some of these cases, there are good reasons to deny that such comparisons are possible (for an excellent review and discussion see Greaves and Lederman 2016).

In cases where interpersonal value comparisons are impossible or different deontological rules conflict, a decision must nevertheless be made but consequentialist (in cases of the former type) or deontological (in cases of the latter type) commitments on the foundational level do not have the resource to explain how the moral status of the acts is determined. We assume (following Binmore) that the moral status of the acts is determined in these cases by the implicit social contract (if such a contract exists). By ‘implicit social contract’ we refer to a set of norms in a society that determines how such cases ought to be handled.

We do not argue that such a set of norms always exists. However, in many cases there are norms that cover a wide range of distributional problems. When such norms do exist, their normative significance is rooted in the mutual agreement of all people in the given society to comply with them.

There might be several normative restrictions one would want to impose on the set of normatively permissible possible social contracts that can ground a given moral principle in a society. Nonetheless, the set of restrictions that we have to impose in order for our argument to hold is very limited. The only constraint imposed on this set is that it will only contain actual norms, i.e. norms that most members of society are actually willing to comply with. We understand this restriction in terms of the given norm being a (subgame-perfect) Nash equilibrium in the infinitely repeated game that best describes the relevant social dynamic.

The term ‘best describes’ is obviously vague. However, to the extent that game-theoretic models are able to represent the strategic nature of certain social dynamics (and we assume that they sometimes do), it seems theoretically kosher to assign to features of such models (such as the set of equilibria in a given model) a normative role that applies to the social reality that is the target phenomenon of the model. To be sure, a model is never a fully accurate representation of the target phenomenon, which, for instance, is why we demand only that most people in society comply with the norm. Be that as it may, this does not mean that the model inaccurately represents the features of reality it is designed to represent.

Our (and Binmore’s) approach clearly allows for different moral norms to apply in different societies (because infinitely repeated games usually have multiple Nash equilibria). However, in allowing this we do not deny that some moral rules are objective (in the sense that they apply in the same way in all societies). Our claim is modest: in some cases where there are conflicts of interest with no deontological or consequentialist way to resolve them, the conflicts should be (and are) resolved by mutual agreement.

As modest as is this endorsement of contractualism, it is surely non-trivial. Our aim in this paper is not to present a comprehensive defence of Binmore’s framework. Our aim, rather, is to point to one advantage it has, i.e. its ability to provide an explanation for the determination of the threshold in cases in which threshold deontology intuitions arise. We achieve this by introducing an element of uncertainty into the game played by the relevant agents in cases where the intuitions arise. In the next section we show how, by doing so, we can get the result that in some cases a threshold deontology norm, i.e. a norm of the form ‘always obey rule R, unless by breaking it you can achieve a value that exceeds threshold T, and in this case break R’ arises as a subgame-perfect Nash equilibrium in an infinitely repeated game. Importantly, in our model, and unlike the case in all alternative accounts of threshold deontology we are aware of (see the list of references at the beginning of this section), constraints on the threshold, T, are determined endogenously. This is a clear advantage of our account.

We demonstrate by considering a simple game that represents the interaction between the government and oil and gas companies. This leads us to show that in the infinitely repeated version of this game, there exists a subgame-perfect equilibrium that supports a threshold deontology norm in which the government keeps its promises as long as breaking its promises is not very beneficial, and there exists no equilibrium in which the government never breaks its promises.

This result constitutes a contractualist justification for threshold deontology in an interesting family of cases and the threshold it points to is not arbitrary but rather determined by strategic considerations. According to our account, the government’s justification for breaking its promises is that it was not a ‘real’ promise to begin with: there was no Nash equilibrium in which this promise is always kept. In other words, the firm already knew (if it was rational) that if enough oil/gas were to be discovered, tax laws would be changed.

As our results hold only when the probability distribution over the possible values of X is wide enough, it also nicely explains the difference between the low-risk investor and the high-risk investor presented above.

4. Mathematical Model and Analysis

4.1. Starting Point: A Repeated Game between a Government and a Firm

Our starting point is the well-known distinction between a one-shot game and a repeated play of this game (see e.g. Osborne and Rubinstein 1994). In many cases, most famously that of the prisoner’s dilemma, in a single-shot game the strategic considerations of the players force non-cooperation between them, leading to a socially inferior ‘Pareto-dominated’ outcome in every equilibrium of the game. By contrast, when the same game is played repeatedly, players can punish and reward each other over the long term, incentivizing cooperation, which leads to an outcome that benefits all. It turns out that there are typically many possible equilibria of the repeated game, each one of them corresponding to certain ‘rules’ of long-term play. The well-known ‘folk theorem’ characterizes the possible outcomes of these possible equilibria in a precise way. One may view the set of rules that lead to a Pareto-efficient equilibrium as a superior social contract.

Consider the following simple model of the interaction between two players, the government and a firm, in cases of the type discussed in section 1: the government can choose between levying low taxes L and high taxes H , while the firm may choose between exerting effort E (e.g. searching for oil) or shirking S (i.e. putting only an insignificant effort into oil exploration). ⁶ The utilities of the game are listed in Table 1. The game is set in a way that if the government decides on choosing low taxes then the firm will prefer exerting effort, leading to high utilities for both the firm and the government. If, on the other hand, the government insists on high taxes then the firm will prefer shirking effort, leading to low utilities for both. The catch is that levying high taxes ( H ) is a dominant strategy for the government.

Table 1. The basic government-firm game

In game-theoretic terms, the game is solvable by repeated elimination of strictly dominated strategies and the only Nash equilibrium point is ( H,S ). In a one-shot play of this game, the government will just levy high taxes ( H is dominant for the government) and, expecting that, the firm will shirk effort ( S is the best reply of the firm to the government’s H ), leading to an inferior, Pareto-dominated, outcome for both.

The folk theorem tells us that in an infinitely repeated play of this game there is a Nash equilibrium in which the efficient outcome ( L,E ) is played in every turn. Any equilibrium of this sort must be supported by a profile of strategies in which the firm punishes the government for any deviation from the equilibrium (as in the absence of a punishment the government has no incentive to play the dominated act).

The formal setting assumes that players are risk-neutral and aim to optimize their discounted sum of utilities, $\mathop \sum \nolimits_{t = 0}^\infty {\delta ^t}{u_t}$ , where 0<δ<1 is the discount factor, and u _t is the utility they get at time t. As long as the discount factor is not too small (i.e. as long as players care enough about the future) the desired ( L,E ) outcome is obtained using (for example) the following ‘grim-trigger’ strategies that are in equilibrium (formally they are in a subgame-perfect Nash equilibrium):

Grim-Trigger Strategies. Initially the government levies low taxes (plays L ) and the firm exerts effort (plays E ). Both of them continue to do so unless at any point one (or both) of them deviate from this ( L,E ) play. If such a deviation occurs, then from that point on the government will always play H and the firm will always play S .

A plausible (and quite common) interpretation of this phenomenon is to view it as a reduction of (or an explanation of the emergence of) a deontological principle (‘player 2 should not betray the trust of player 1’) to (by) a consequentialist one (‘player 2 must maximize utility in the long run’).

Let us now go over the standard analysis of this specific game, showing that these grim-trigger strategies are in a subgame-perfect equilibrium. The basic argument goes as follows: at any given stage, the government may deviate to H to get a utility of 4 at this stage, and then, since the firm is playing grim-trigger, it will start shirking and continue playing S forever. Now the best that the government can do is play H and win 1 in all subsequent stages for a total discounted (to this time point) utility of $\left( {4 + {\delta \over {1 - \delta }}} \right)$ . On the other hand, continuing to cooperate will give the government a utility of $\left( {3 + {{3\delta } \over {1 - \delta }}} \right)$ , and therefore deviation is not profitable as long as the former utility is not greater than the latter, $\left( {4 + {\delta \over {1 - \delta }}} \right)\; \le \;\left( {3 + {{3\delta } \over {1 - \delta }}} \right)$ , i.e. when δ≥1/3. For the firm things are even simpler since it is already making the most that it can in every stage of the game.

4.2. Stochastic Stakes

We now introduce the crucial feature of our model: before every stage in which the basic game is played, a move by nature occurs. Nature randomly chooses the size of the ‘stakes’ in this round and all values in the game in this stage are scaled by this random number (as deonstrated in Table 2). Specifically, in each stage t of the repeated game, nature chooses the stake x _t according to the fixed commonly known distribution F . Then the players need to play their actions (a _t ,b _t ), which may depend on the entire history of play a _i , b _i , x _i for all i<t as well as on the current stakes x _t . The utilities of the players in stage t are linear in x=x _t and are given by the following table, which is just a scaling of the previous game by the stochastically chosen stakes x .

Table 2. The government-firm game with stochastic stakes

We continue assuming the standard model in which players are risk-neutral and aim to optimize their discounted sum of utilities, $\mathop \sum \nolimits_{t = 0}^\infty {\delta ^t}{u_i}\left( {{a_t},{b_t}} \right)$ , where 0<δ<1 is the discount factor. Our analysis will not be sensitive to the exact notion of equilibrium considered and in fact all our statements hold equally well for subgame-perfect Nash equilibria and arbitrary Nash equilibria.

Our results and conceptual conclusions in this model can be summarized by the following three points:

1. (1) If the distribution F is ‘mild’ enough (i.e., has no ‘extreme values’) then the previous cooperation achieved through the grim-trigger strategies is maintained. Conceptually, the emergence of the deontological principle of ‘trust’ (the government must not betray the trust of the firm by levying high taxes) occurs even in this stochastic setting.

2. (2) If the distribution F may take extreme values, then, in every equilibrium, the government levies high taxes whenever the stakes x _t are sufficiently high. Conceptually, there is no way that the deontological principle of trust can emerge and be maintained in equilibrium since no rational government will be able to resist levying high taxes in extreme situations.

3. (3) However, even when the distribution can take also extreme values, there is an equilibrium in which the cooperation is maintained in all stages, except those with an extreme value of x _t . The threshold for being considered ‘extreme’ depends on the utilities of the game and on the discount factor. There is a range of possible thresholds that can support equilibrium, each leading to a different equilibrium. Conceptually, this explains the emergence of a threshold deontology in which the government does not betray the firm, except in extreme situations. Crucially, as the firm expects the government to ‘defect’ in extreme situations, it does not punish the government for doing so and continues to cooperate in later stages. While this threshold deontology (‘maintain trust except in extreme cases’) achieves lower utilities than full cooperation (which as we showed cannot be achieved), it can get very close to it, always achieving higher utilities than defection.

4.3. Detailed Analysis ⁷

Our first observation is that the analysis showing that the equilibrium set by grim-trigger strategies continues to hold even when x is coming from a sufficiently mild distribution F . This implies that the cooperative social norms continue to hold even when the stakes are stochastic, but not extremely so.

Let us denote the expected value of the distribution F by μ=E _x∼F [x].

Theorem 1. If the support of F is contained in $\left[0,\;{{2\delta \mu } \over {1 - \delta }}\right]$ then the grim-trigger strategies described above are in a subgame-perfect Nash equilibrium.

The proof, together with all other proofs in this paper, appears in the Appendix.

We will use, as a running example, a discount factor of a ‘10% interest rate’, i.e. δ=0.9. With this discount factor, we see that as long as the highest possible value coming from the distribution is at most 18 times the expected value of the distribution, then we maintain the cooperative outcome ( L,E ) using the same grim-trigger strategies.

For the rest of this analysis, we will use, as a running example, a distribution F that is not supported on this subrange. Specifically, we will consider the exponential distribution $F\left( x \right) = 1 - {{\rm{e}}^{ - x}}$ (for x>0, with density function $\;f\left( x \right) = {e^{ - x}}$ ), so the expected value is μ=E[x]=1. The exponential distribution obviously has infinite support and so does not satisfy the assumptions of the lemma, which leads us to the following analysis.

We now get our first simple yet interesting observation: it is impossible to maintain cooperation for extreme values of x _t ’s! Let us start by looking at the equilibrium studied above and see why these grim-trigger strategies are no longer in equilibrium: assume that at some stage we have x=x _t >>μ and now the government has to choose an action for this stage. As before, continuing to cooperate yields a utility of $3x + {{3\delta \mu } \over {1 - \delta }}\;$ (discounted to that time step) but deviation would achieve a utility of $4x + {{\delta \mu } \over {1 - \delta }};$ this is strictly higher whenever $x \gt \;{{2\delta \mu } \over {1 - \delta }}$ , which implies that the grim-trigger strategies are not in equilibrium if ${\rm{Pr}}[\;x \gt {{2\delta \mu } \over {1 - \delta }}] \gt 0$ , which is indeed the case in our distribution. It turns out that this is not due to a deficiency of the grim-trigger strategies, but rather to the fact that no fully cooperative Nash equilibrium exists when F’s support includes sufficiently high values.

Theorem 2. In any pair of strategies that are in a Nash equilibrium, at any time (that has a non-zero probability of being reached) when ${x_t} \! \gt \;{{3\delta \mu } \over {1 - \delta }}\;$ , the government plays H.

Returning to our running example with δ=0.9 and the exponential distribution (with expectation μ=1), the government will always levy high taxes whenever nature chooses an extreme value of x _t >27 and, in particular, full cooperation is not possible.

We now move on to establish the possibility of partial cooperation, i.e. the emergence of threshold deontology. Specifically, we will show that it is possible to cooperate on ‘regular’ values of x while allowing, without punishing, deviations for ‘high’ values of x.

Definition. The θ-threshold grim-trigger strategies for the government and the firm are as follows:

1. (I) When x _t >θ, the government plays H and the firm plays S .

2. (II) If, previously, the government always played L and the firm always played E when x _j ≤θ, $j \lt t$ , then the government plays L and the firm plays E when x _t ≤θ.

3. (III) If anytime in a previous round when x _j ≤θ, $j \lt t$ , either the government did not play L or the firm did not play E , then the government plays H and the firm plays S .

In other words, the participants play ( H,S ) when x _t >θ and play grim-trigger strategies when x _t ≤θ, without punishing any behaviour taken when x _t >θ.

We will show that such strategies are in equilibrium. The threshold θ is not totally arbitrary, and to define sufficient conditions for it we will require the following definition.

Definition: For a distribution F and a real value θ, define the θ-trimmed expected value as ${\mu _\theta } = {\mu _\theta }\left( F \right) = {E_{x\sim F}}\left[ {x \cdot {1_{x \le \theta }}} \right] = F\left( \theta \right) \cdot {E_{x\sim F}}[x|x\; \le \theta ]$ .

Clearly, by definition, ${\mu _\theta }\;$ is (weakly) increasing in θ, approaching the expected value of F as θ approaches infinity (or equalling it if θ exceeds the upper bound on the support of F).

Theorem 3. Assume ${\theta \over {{\mu _\theta }}} \le {{2\delta } \over {1 - \delta }}\;$ ; then the θ-threshold grim-trigger strategies for the government and the firm are in a subgame-perfect Nash equilibrium.

Let us consider our running example of δ=0.9 and the exponential distribution $F\left( x \right) = 1 - {{\rm{e}}^{ - x}}$ with density function $\;f\left( x \right) = {e^{ - x}}$ and expectation μ=1. One may calculate ${\mu _\theta } = \;\mathop \int \nolimits_0^\theta x\;{e^{ - x}}dx\; = \;1 - \left( {1 + \theta } \right){e^{ - \theta }}$ , and so this lemma states that we get cooperation when ${\theta \over {1 - \left( {1 + \theta } \right){e^{ - \theta }}}} \le {{2\delta } \over {1 - \delta }}$ . The function of θ on the LHS is unimodal: decreasing for small values and then increasing. For our running example with δ=0.9 the condition is satisfied when 0.12… ≤θ ≤17.99…. Indeed, when θ is too small, small enough values of x that require cooperation happen so rarely that punishment by the firm is not effective. When θ is too large, we have seen already that the government must levy high taxes.

The utilities achieved by these threshold grim-trigger strategies are (x,x) when x _t > θ and (3x,3x) when x _t ≤ θ. Thus, the expected utility of each of the two players in every stage is given by $\mu + 2{\mu _\theta }$ . In particular, taking the highest possible threshold θ≈ 17.99 yields a utility of 2.9999…, very close to 3, which is what would have been achieved by perfect cooperation. Taking the lowest possible threshold θ≈0.12 would only yield a utility of 1.013…, very close to 1, which is what would have been achieved by defection.

As we can see from this example, if we can influence the choice of the equilibrium, then choosing a higher defection threshold is preferable from a social welfare point of view as it brings us as close to possible to the scenario of full cooperation. While we do not claim that this must be the case for every game and every distribution on the stakes, it does seem to be the typical case. From this point of view, one might draw a general rule of thumb that recommends that governments and societies choose norms (‘equilibria’) that are as close as possible to deontological even when adopting fully deontological norms is impossible.

5. Conclusion

We have shown that in a family of games that can plausibly be viewed as representing the basic dynamic between the government and the private sector, in the relevant class of cases there exists an equilibrium that supports a threshold deontology norm, i.e. an equilibrium in which the government keeps its promises as long as breaking them is not beneficial ‘enough’, but breaks them in extreme cases. However, there exists no equilibrium that supports a norm in which the government never breaks its promises.

We have also shown that in some such ‘threshold deontology equilibria’, the government and the private sector continue cooperating, following the government’s deviation. Thus, at least in the type of case that our model captures, the threat of long-term economic damage from lack of regulatory stability is not credible. We have argued that, by adopting a contractualist point of view, this mathematical phenomenon can be seen as supplying solid foundations for threshold deontology.

As demonstrated at the end of the previous section, in some cases our account also shows which market norms are more beneficial from a social point of view. Thus, in cases in which governments have the ability to influence social norms our account can provide (qualitative) guidance for how to do so.

Although in this paper we have concentrated on the cases of ex post regulatory changes, the general structure of the argument can be used to support threshold deontology norms in other contexts. One obvious context that comes to mind is that of taxation of so-called ‘Unicorns’. The exponential growth in the earnings and market value of the big tech companies is challenging the fiscal regime in a way that is similar in many respects to the effect of discoveries of large oil and gas resources. The market value of the top big 5 (Apple, Amazon, Google, Microsoft and Facebook) is almost 25% of the total S&P 500, with market value similar to the GDP of Britain, Germany and France combined. The discussion on the public ‘fair’ share in those huge profits that partly depend on public resources is still ongoing. We anticipate that the huge and growing ‘stakes’ on the table may be perceived as an extreme case in an analogous way to large oil and gas discoveries. Our model could assist in determining the main factors that should be considered when thinking about what is the most efficient and the fair way to handle these cases.