Hostname: page-component-5b777bbd6c-7sgmh Total loading time: 0 Render date: 2025-06-19T15:03:40.841Z Has data issue: false hasContentIssue false
  • English
  • Français

Phragmén–Lindelöf principles and Julia limiting directions of quasiregular mappings

Part of: Other generalizations Geometric function theory

Published online by Cambridge University Press:  11 June 2025

ALASTAIR N. FLETCHER Open the ORCID record for ALASTAIR N. FLETCHER [Opens in a new window]  and
JULIE M. STERANKA
ALASTAIR N. FLETCHER*
Affiliation:
Department of Mathematical Sciences, https://ror.org/012wxa772Northern Illinois University, DeKalb, IL 60115, USA
JULIE M. STERANKA
Affiliation:
Department of Mathematics, https://ror.org/020f3ap87The University of Tennessee, Knoxville, TN 37966, USA (e-mail: jsterank@utk.edu)
*
e-mail: afletcher@niu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the set of Julia limiting directions of a transcendental-type K-quasiregular mapping 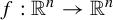$f:\mathbb {R}^n\to \mathbb {R}^n$ must contain a component of a certain size, depending on the dimension n, the maximal dilatation K, and the order of growth of f. In particular, we show that if the order of growth is small enough, then every direction is a Julia limiting direction. We also show that if every component of the set of Julia limiting directions is a point, then f has infinite order. The main tool in proving these results is a new version of a Phragmén–Lindelöf principle for sub-F-extremals in sectors, where we allow for boundary growth of the form 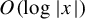$O( \log |x| )$ instead of the previously considered 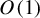$O(1)$ bound.

Keywords

Julia limiting directionsquasiregular mappingsPhragmén–Lindelöf principle

MSC classification

Secondary: 30C65: Quasiconformal mappings in $^n$, other generalizations 31C45: Other generalizations (nonlinear potential theory, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , First View , pp. 1 - 19
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Baker, I. N.. The domains of normality of an entire function. Ann. Acad. Sci. Fenn. Ser. A I Math. 1 (1975), 277–283.10.5186/aasfm.1975.0101CrossRefGoogle Scholar
Bergweiler, W.. Fixed points of composite entire and quasiregular maps. Ann. Acad. Sci. Fenn. Math. 31 (2006), 523–540.Google Scholar
Bergweiler, W.. Fatou–Julia theory for non-uniformly quasiregular maps. Ergod. Th. & Dynam. Sys. 33 (2013), 1–23.10.1017/S0143385711000915CrossRefGoogle Scholar
Bergweiler, W. and Nicks, D. A.. Foundations for an iteration theory of entire quasiregular maps. Israel J. Math. 201(1) (2014), 147–184.10.1007/s11856-014-1081-4CrossRefGoogle Scholar
Botvinnik, V. and Miklyukov, V. M.. A theorem of Phragmén–Lindelöf-type for $n$ -dimensional mappings with bounded distortion. Sib. Mat. Zh. 21(2) (1980), 232–235, 240.Google Scholar
Bredon, G. E.. Topology and Geometry. Springer-Verlag, New York, 1997.Google Scholar
Essén, M.. A generalization of the M. Riesz theorem on conjugate functions and the Zygmund $L\;\log\;L$ -theorem to ${\mathbb{R}}^d$ , $d\ge 2$ . Ann. Acad. Sci. Fenn. Ser. A I Math. 15(1) (1990), 83–105.10.5186/aasfm.1990.1509CrossRefGoogle Scholar
Fletcher, A. N.. On Julia limiting directions in higher dimensions. Comput. Methods Funct. Theory 21 (2021), 587–603.10.1007/s40315-021-00381-wCrossRefGoogle Scholar
Gentili, G., Stoppato, C. and Struppa, D. C.. A Phragmén–Lindelöf principle for slice regular functions. Bull. Belg. Math. Soc. Simon Stevin, 18(4) (2011), 749–759.CrossRefGoogle Scholar
Granlund, S., Lindqvist, P. and Martio, O.. Conformally invariant variational integrals. Trans. Amer. Math. Soc. 277 (1983), 43–73.CrossRefGoogle Scholar
Granlund, S., Lindqvist, P. and Martio, O.. Phragmén–Lindelöf’s and Lindelöf’s theorems. Ark. Mat. 23(1) (1985), 103–128.10.1007/BF02384420CrossRefGoogle Scholar
Granlund, S., Lindqvist, P. and Martio, O.. Note on the PWB-method in the nonlinear case. Pacific J. Math. 125 (1986), 381–395.10.2140/pjm.1986.125.381CrossRefGoogle Scholar
Heinonen, J., Kipeläinen, T. and Martio, O.. Nonlinear Potential Theory of Degenerate Elliptic Equations. Oxford University Press, New York, 1993.Google Scholar
Kuroda, T.. On the uniform meromorphic functions with the set of capacity zero of essential singularities. Tohoku Math. J. (2) 3 (1951), 257–269.10.2748/tmj/1178245478CrossRefGoogle Scholar
Martio, O., Miklyukov, V. and Vuorinen, M.. Estimates for the energy integral of quasiregular mappings on Riemannian manifolds and isoperimetry. Czechoslovak Math. J. 51(126)(3) (2001), 585–608.10.1023/A:1013788107061CrossRefGoogle Scholar
Momm, S.. A Phragmén–Lindelöf theorem for plurisubharmonic functions on cones in ${\mathbb{C}}^n$ . Indiana Univ. Math. J. 41(3) (1992), 861–867.10.1512/iumj.1992.41.41046CrossRefGoogle Scholar
Nicks, D. A. and Sixsmith, D. J.. Periodic domains of quasiregular maps. Ergod. Th. & Dynam. Sys. 38(6) (2018), 2321–2344.10.1017/etds.2016.116CrossRefGoogle Scholar
Qiao, J.. On limiting directions of Julia sets. Ann. Acad. Sci. Fenn. Math. 26(2) (2001), 391–399.Google Scholar
Qiu, L. and Wu, S.. Radial distributions of Julia sets of meromorphic functions. J. Aust. Math. Soc. 81(3) (2006), 363–368.10.1017/S1446788700014361CrossRefGoogle Scholar
Rickman, S.. Quasiregular Mappings (Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge / A Series of Modern Surveys in Mathematics, 26). Springer-Verlag, Heidelberg, 1993.10.1007/978-3-642-78201-5CrossRefGoogle Scholar
Rickman, S. and Vuorinen, M.. On the order of quasiregular mappings. Ann. Acad. Sci. Fenn. Ser. A I Math. 7 (1982), 221–231.10.5186/aasfm.1982.0727CrossRefGoogle Scholar
Wang, J. and Chen, Z.. Limiting directions of Julia sets of entire solutions to complex differential equations. Acta Math. Sci. Ser. B (Engl. Ed.) 37(1) (2017), 97–107.Google Scholar
Wang, J. and Yao, X.. On Julia limiting directions of meromorphic functions. Israel J. Math. 238 (2020), 405–430.10.1007/s11856-020-2037-5CrossRefGoogle Scholar
Wang, S.. On radial distribution of Julia sets of meromorphic functions. Taiwanese J. Math. 11 (2007), 1301–1313.Google Scholar
Yoshida, H.. On subharmonic functions dominated by certain functions. Israel J. Math. 54 (1986), 366–380.10.1007/BF02764964CrossRefGoogle Scholar
Yoshida, H.. Harmonic majorization of a subharmonic function on a cone or on a cylinder. Pacific J. Math. 148(2) (1991), 369–395.10.2140/pjm.1991.148.369CrossRefGoogle Scholar
Zheng, J.-H., Wang, S. and Huang, Z.-G.. Some properties of Fatou and Julia sets of transcendental meromorphic functions. Bull. Aust. Math. Soc. 66(1) (2002), 1–8.Google Scholar