On the reduction of a random basis

Abstract

For p ≤ n, let b₁⁽ⁿ⁾,...,b_p⁽ⁿ⁾ be independent random vectors in $\mathbb{R}^n$ with the same distribution invariant by rotation and without mass at the origin. Almost surely these vectors form a basis for the Euclidean lattice they generate. The topic of this paper is the property of reduction of this random basis in the sense of Lenstra-Lenstra-Lovász (LLL). If $\widehat b_{1}^{(n)},\ldots, \widehat b_p^{(n)}$ is the basis obtained from b₁⁽ⁿ⁾,...,b_p⁽ⁿ⁾ by Gram-Schmidt orthogonalization, the quality of the reduction depends upon the sequence of ratios of squared lengths of consecutive vectors $r_j^{(n)} = \Vert \widehat b^{(n)}_{n-j+1}\Vert^2 / \Vert \widehat b^{(n)}_{n-j} \Vert^2$ 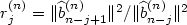, j = 1,...,p - 1. We show that as n → +∡ the process $(r_j^{(n)}-1,j\geq 1)$ 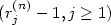tends in distribution in some sense to an explicit process $({\mathcal R}_j -1,j\geq 1)$ 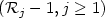; some properties of the latter are provided. The probability that a random random basis is s-LLL-reduced is then showed to converge for p = n - g, and g fixed, or g = g(n) → +∞.