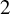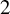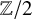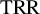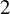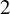Introduction
Let k be a field. Let us recall that Milnor conjectured, in [Reference MilnorMil71], [Reference MilnorMil70], that a certain canonical map of graded rings
should be an isomorphism. Here,
![]() ${\mathrm {K}}^M_\ast (k)$
is the Milnor K-theory of k, and
${\mathrm {K}}^M_\ast (k)$
is the Milnor K-theory of k, and
![]() $I:=\ker (rk\colon {\mathrm {W}}^s(k)\to \mathbb {Z}/2)$
is the augmentation ideal of the Witt group
$I:=\ker (rk\colon {\mathrm {W}}^s(k)\to \mathbb {Z}/2)$
is the augmentation ideal of the Witt group
![]() ${\mathrm {W}}^s(k)$
of symmetric forms over k. This conjecture was proved in [Reference KatoKat82] when k has characteristic
${\mathrm {W}}^s(k)$
of symmetric forms over k. This conjecture was proved in [Reference KatoKat82] when k has characteristic
![]() $2$
, and subsequently in [Reference Orlov, Vishik and VoevodskyOVV07, Reference VoevodskyVoe03, Reference MorelMor05] in characteristic different from
$2$
, and subsequently in [Reference Orlov, Vishik and VoevodskyOVV07, Reference VoevodskyVoe03, Reference MorelMor05] in characteristic different from
![]() $2$
.
$2$
.
The starting point of our paper is the following, somewhat overloaded observation. On one side of this isomorphism, we have a ‘symbolic version’
![]() ${\mathrm {K}}^M_\ast (k)$
of the algebraic K-theory spectrum
${\mathrm {K}}^M_\ast (k)$
of the algebraic K-theory spectrum
![]() ${\mathrm {K}}(k)$
of k. On the other side, we have the Witt group
${\mathrm {K}}(k)$
of k. On the other side, we have the Witt group
![]() ${\mathrm {W}}^s(k)$
, which is
${\mathrm {W}}^s(k)$
, which is
![]() $\pi _0$
of the
$\pi _0$
of the
![]() $\mathbb {Z}/2$
-geometric fixed-points spectrum of a certain canonical
$\mathbb {Z}/2$
-geometric fixed-points spectrum of a certain canonical
![]() $\mathbb {Z}/2$
-equivariant refinement
$\mathbb {Z}/2$
-equivariant refinement
![]() ${\mathrm {KR}}(k)$
of
${\mathrm {KR}}(k)$
of
![]() ${\mathrm {K}}(k)$
(see [CDH+20a, CDH+20b]). One may then wonder if a similar relationship holds for other functors closely related to algebraic K-theory. One does not need to look far for another such example, which is already provided in Kato’s proof of Milnor’s conjecture in characteristic
${\mathrm {K}}(k)$
(see [CDH+20a, CDH+20b]). One may then wonder if a similar relationship holds for other functors closely related to algebraic K-theory. One does not need to look far for another such example, which is already provided in Kato’s proof of Milnor’s conjecture in characteristic
![]() $2$
: The de Rham complex
$2$
: The de Rham complex
![]() $\Omega ^\ast _k$
is a ‘symbolic version’ of the topological Hochschild homology spectrum
$\Omega ^\ast _k$
is a ‘symbolic version’ of the topological Hochschild homology spectrum
![]() ${\mathrm {THH}}(k)$
, and
${\mathrm {THH}}(k)$
, and
![]() ${\mathrm {THH}}(k)$
also admits a canonical
${\mathrm {THH}}(k)$
also admits a canonical
![]() $\mathbb {Z}/2$
-equivariant refinement
$\mathbb {Z}/2$
-equivariant refinement
![]() ${\mathrm {THR}}(k)$
. The calculation of [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Corollary 5.2] provides an isomorphism between
${\mathrm {THR}}(k)$
. The calculation of [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Corollary 5.2] provides an isomorphism between
![]() $\pi _0$
of the
$\pi _0$
of the
![]() $\mathbb {Z}/2$
-geometric fixed points of this spectrum and
$\mathbb {Z}/2$
-geometric fixed points of this spectrum and
![]() $(k\otimes _S k)/2$
, where
$(k\otimes _S k)/2$
, where
![]() $S\leq k$
is the subfield generated by the squares. The result analogous to Milnor’s conjecture is then an isomorphism
$S\leq k$
is the subfield generated by the squares. The result analogous to Milnor’s conjecture is then an isomorphism
where J is the kernel of the multiplication map
![]() $\mu \colon (k\otimes _S k)/2\to k/2$
. Let us point out that if
$\mu \colon (k\otimes _S k)/2\to k/2$
. Let us point out that if
![]() $2$
is a unit in k, the source and target of this map are clearly zero, so that this statement has content only when the characteristic of k is
$2$
is a unit in k, the source and target of this map are clearly zero, so that this statement has content only when the characteristic of k is
![]() $2$
. It seems to be a standard result that this map is an isomorphism, and it plays an important role in the proof of [Reference KatoKat82, Lemma 7(3)] (see [Reference ArasonAra20] for a proof, which we recast in Lemma 3.6). The main goal of our paper is to establish an analogous result for topological restriction homology, whose ‘symbolic version’ is the de Rham-Witt complex of Bloch, Deligne and Illusie [Reference IllusieIll79].
$2$
. It seems to be a standard result that this map is an isomorphism, and it plays an important role in the proof of [Reference KatoKat82, Lemma 7(3)] (see [Reference ArasonAra20] for a proof, which we recast in Lemma 3.6). The main goal of our paper is to establish an analogous result for topological restriction homology, whose ‘symbolic version’ is the de Rham-Witt complex of Bloch, Deligne and Illusie [Reference IllusieIll79].
Let
![]() ${\mathrm {W}}_{\langle 2^\bullet \rangle }\Omega ^\ast _k$
be the
${\mathrm {W}}_{\langle 2^\bullet \rangle }\Omega ^\ast _k$
be the
![]() $2$
-typical de Rham-Witt complex of k. We will take the definition of [Reference CosteanuCos08] as the initial object in the category of
$2$
-typical de Rham-Witt complex of k. We will take the definition of [Reference CosteanuCos08] as the initial object in the category of
![]() $2$
-typical Witt complexes over k (see also [Reference Hesselholt and MadsenHM04]). For all integers
$2$
-typical Witt complexes over k (see also [Reference Hesselholt and MadsenHM04]). For all integers
![]() $n\geq 0$
, let
$n\geq 0$
, let
![]() ${\mathrm {TR}}^{n+1}(k;2)$
be the
${\mathrm {TR}}^{n+1}(k;2)$
be the
![]() $2$
-typical
$2$
-typical
![]() $(n+1)$
-truncated topological restriction homology of [Reference Bökstedt, Hsiang and MadsenBHM93] (see also [Reference Antieau and NikolausAN21]). Similarly to the relation between Milnor K-theory and algebraic K-theory,
$(n+1)$
-truncated topological restriction homology of [Reference Bökstedt, Hsiang and MadsenBHM93] (see also [Reference Antieau and NikolausAN21]). Similarly to the relation between Milnor K-theory and algebraic K-theory,
![]() ${\mathrm {W}}_{\langle 2^\bullet \rangle }\Omega ^\ast _k$
and the homotopy groups of
${\mathrm {W}}_{\langle 2^\bullet \rangle }\Omega ^\ast _k$
and the homotopy groups of
![]() ${\mathrm {TR}}^{n+1}(k;2)$
agree in low degrees, and the former should be consider the symbolic version of the latter (see [Reference HesselholtHes04] and [Reference Geisser and HesselholtGH99, §4]). We recall that the spectrum
${\mathrm {TR}}^{n+1}(k;2)$
agree in low degrees, and the former should be consider the symbolic version of the latter (see [Reference HesselholtHes04] and [Reference Geisser and HesselholtGH99, §4]). We recall that the spectrum
![]() ${\mathrm {TR}}^{n+1}(k;2)$
is defined as the
${\mathrm {TR}}^{n+1}(k;2)$
is defined as the
![]() $C_{2^n}$
-fixed points of a
$C_{2^n}$
-fixed points of a
![]() $C_{2^n}$
-equivariant structure on
$C_{2^n}$
-equivariant structure on
![]() ${\mathrm {THH}}(k)$
, where
${\mathrm {THH}}(k)$
, where
![]() $C_{2^n}$
is the cyclic group of order
$C_{2^n}$
is the cyclic group of order
![]() $2^n$
. This admits a
$2^n$
. This admits a
![]() $\mathbb {Z}/2$
-equivariant refinement
$\mathbb {Z}/2$
-equivariant refinement
![]() ${\mathrm {TRR}}^{n+1}(k;2)$
, constructed by extending the
${\mathrm {TRR}}^{n+1}(k;2)$
, constructed by extending the
![]() $C_{2^n}$
-equivariant structure on
$C_{2^n}$
-equivariant structure on
![]() ${\mathrm {THH}}(k)$
to an equivariant spectrum
${\mathrm {THH}}(k)$
to an equivariant spectrum
![]() ${\mathrm {THR}}(k)$
for the dihedral group
${\mathrm {THR}}(k)$
for the dihedral group
![]() $D_{2^n}$
of order
$D_{2^n}$
of order
![]() $2^{n+1}$
. The fixed-point spectrum
$2^{n+1}$
. The fixed-point spectrum
then inherits the structure of a
![]() $\mathbb {Z}/2$
-spectrum since
$\mathbb {Z}/2$
-spectrum since
![]() $\mathbb {Z}/2$
is the Weyl group of
$\mathbb {Z}/2$
is the Weyl group of
![]() $C_{2^n}$
in
$C_{2^n}$
in
![]() $D_{2^n}$
. This construction is carried out in [Reference HøgenhavenHøg16] and [Reference Dotto, Moi and PatchkoriaDMP24, §1], and we review it in §1. There is then a canonical ring homomorphism
$D_{2^n}$
. This construction is carried out in [Reference HøgenhavenHøg16] and [Reference Dotto, Moi and PatchkoriaDMP24, §1], and we review it in §1. There is then a canonical ring homomorphism
where
![]() $(-)^{\phi \mathbb {Z}/2}$
denotes the geometric fixed-points functor, and we let
$(-)^{\phi \mathbb {Z}/2}$
denotes the geometric fixed-points functor, and we let
![]() $J_{\langle 2^n \rangle }$
be its kernel. There are operators between these spectra
$J_{\langle 2^n \rangle }$
be its kernel. There are operators between these spectra
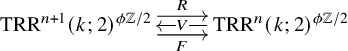
which correspond to the usual respective maps R, V and F on
![]() ${\mathrm {TR}}^{n+1}(k;2)$
under the restriction map above. There is also a map
${\mathrm {TR}}^{n+1}(k;2)$
under the restriction map above. There is also a map
of order
![]() $2$
, which is induced by the action of the Weyl group of
$2$
, which is induced by the action of the Weyl group of
![]() $\mathbb {Z}/2$
in the quotient
$\mathbb {Z}/2$
in the quotient
![]() $D_{2^{n+1}}/C_{2^n}$
. It is easy to see that all these maps restrict to maps between the kernels
$D_{2^{n+1}}/C_{2^n}$
. It is easy to see that all these maps restrict to maps between the kernels
![]() $J_{\langle 2^n \rangle }$
. The main result of the paper is the following analogue of Milnor’s conjecture.
$J_{\langle 2^n \rangle }$
. The main result of the paper is the following analogue of Milnor’s conjecture.
Theorem 1. Let k be a field of characteristic
![]() $2$
. The maps
$2$
. The maps
![]() $R,F,V$
and
$R,F,V$
and
![]() $d:=1+\sigma $
endow the sequence
$d:=1+\sigma $
endow the sequence
![]() $J_{\langle 2^\bullet \rangle }^\ast /J_{\langle 2^\bullet \rangle }^{\ast +1}$
with the structure of a
$J_{\langle 2^\bullet \rangle }^\ast /J_{\langle 2^\bullet \rangle }^{\ast +1}$
with the structure of a
![]() $2$
-typical Witt complex over k, and the unique map of
$2$
-typical Witt complex over k, and the unique map of
![]() $2$
-typical Witt complexes over k
$2$
-typical Witt complexes over k
is a strict isomorphism.
Let us remark on some special cases of this theorem:
-
i) For
 $\ast =0$
, the isomorphism of Theorem 1 identifies with the modulo
$\ast =0$
, the isomorphism of Theorem 1 identifies with the modulo
 $2$
reduction of the isomorphism
$2$
reduction of the isomorphism
 ${\mathrm {W}}_{\langle 2^n\rangle }(k)\cong \pi _0{\mathrm {TR}}^{n+1}(k;2)$
of [Reference Hesselholt and MadsenHM97, Theorem F], where
${\mathrm {W}}_{\langle 2^n\rangle }(k)\cong \pi _0{\mathrm {TR}}^{n+1}(k;2)$
of [Reference Hesselholt and MadsenHM97, Theorem F], where
 ${\mathrm {W}}_{\langle 2^n\rangle }(k)$
is the ring of
${\mathrm {W}}_{\langle 2^n\rangle }(k)$
is the ring of
 $(n+1)$
-truncated
$(n+1)$
-truncated
 $2$
-typical Witt vectors of k.
$2$
-typical Witt vectors of k. -
ii) For
 $\bullet =0$
, the isomorphism of Theorem 1 is the isomorphism
$\bullet =0$
, the isomorphism of Theorem 1 is the isomorphism
 $\Omega ^\ast _k\cong J^\ast /J^{\ast +1}$
discussed above.
$\Omega ^\ast _k\cong J^\ast /J^{\ast +1}$
discussed above. -
iii) If k has characteristic different from
 $2$
, then both
$2$
, then both
 $({\mathrm {W}}_{\langle 2^\bullet \rangle }\Omega ^\ast _k)/2$
and
$({\mathrm {W}}_{\langle 2^\bullet \rangle }\Omega ^\ast _k)/2$
and
 ${\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
vanish, so Theorem 1 in fact holds in all characteristics.
${\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
vanish, so Theorem 1 in fact holds in all characteristics. -
iv) If k is perfect of characteristic
 $2$
, then
$2$
, then
 $({\mathrm {W}}_{\langle 2^\bullet \rangle }\Omega ^\ast _k)/2=0$
for
$({\mathrm {W}}_{\langle 2^\bullet \rangle }\Omega ^\ast _k)/2=0$
for
 $\ast>0$
, and
$\ast>0$
, and  $$\begin{align*}({\mathrm{W}}_{\langle2^\bullet\rangle}\Omega^0_k)/2={\mathrm{W}}_{\langle2^\bullet\rangle}(k)/2\cong k.\end{align*}$$
$$\begin{align*}({\mathrm{W}}_{\langle2^\bullet\rangle}\Omega^0_k)/2={\mathrm{W}}_{\langle2^\bullet\rangle}(k)/2\cong k.\end{align*}$$
Similarly, in the case of perfect fields,
 $\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}\cong k$
and
$\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}\cong k$
and
 $J_{\langle 2^\bullet \rangle }=0$
(see [Reference Dotto, Moi and PatchkoriaDMP24, Theorem 4.7]). Thus, Theorem 1 has nontrivial content only for non-perfect fields of characteristic
$J_{\langle 2^\bullet \rangle }=0$
(see [Reference Dotto, Moi and PatchkoriaDMP24, Theorem 4.7]). Thus, Theorem 1 has nontrivial content only for non-perfect fields of characteristic
 $2$
.
$2$
.
We prove the theorem by first explicitly calculating the homotopy groups of
![]() ${\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
in §2.1 (even though we really only need
${\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
in §2.1 (even though we really only need
![]() $\pi _0$
), extending the calculations for perfect fields of [Reference Dotto, Moi and PatchkoriaDMP24, §4.2]. We then use our calculation to provide generators for
$\pi _0$
), extending the calculations for perfect fields of [Reference Dotto, Moi and PatchkoriaDMP24, §4.2]. We then use our calculation to provide generators for
![]() $\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
and
$\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
and
![]() $J_{\langle 2^\bullet \rangle }$
, analogous to the canonical generators
$J_{\langle 2^\bullet \rangle }$
, analogous to the canonical generators
![]() $V^{n-i}\tau _i(a)$
of the Witt vectors (see Propositions 2.9 and 2.16). This allows us to define a Witt-complex structure on
$V^{n-i}\tau _i(a)$
of the Witt vectors (see Propositions 2.9 and 2.16). This allows us to define a Witt-complex structure on
![]() $J_{\langle 2^\bullet \rangle }^\ast /J_{\langle 2^\bullet \rangle }^{\ast +1}$
, and to prove Theorem 1 by induction on
$J_{\langle 2^\bullet \rangle }^\ast /J_{\langle 2^\bullet \rangle }^{\ast +1}$
, and to prove Theorem 1 by induction on
![]() $\bullet $
, using the exact sequences of [Reference CosteanuCos08, Lemma 3.5], in §3.2.
$\bullet $
, using the exact sequences of [Reference CosteanuCos08, Lemma 3.5], in §3.2.
The description of the homotopy groups of
![]() ${\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
is in Theorem 2.7, and it is proved using the pullbacks of [Reference Dotto, Moi and PatchkoriaDMP24, Theorem 2.7]. It is somewhat technical, and we will not state it here, but it is completely explicit. There is, however, a closely related calculation which is more straightforward to state. Let
${\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
is in Theorem 2.7, and it is proved using the pullbacks of [Reference Dotto, Moi and PatchkoriaDMP24, Theorem 2.7]. It is somewhat technical, and we will not state it here, but it is completely explicit. There is, however, a closely related calculation which is more straightforward to state. Let
![]() ${\mathrm {TCR}}(k;2)$
be the
${\mathrm {TCR}}(k;2)$
be the
![]() $2$
-typical real topological cyclic homology spectrum of k, which we may define as the equaliser
$2$
-typical real topological cyclic homology spectrum of k, which we may define as the equaliser
where
![]() ${\mathrm {TRR}}(k;2)$
is the limit of
${\mathrm {TRR}}(k;2)$
is the limit of
![]() ${\mathrm {TRR}}^{n+1}(k;2)$
over the maps R. Let us point out that, by [Reference Dotto, Moi and PatchkoriaDMP24, Theorem A], if
${\mathrm {TRR}}^{n+1}(k;2)$
over the maps R. Let us point out that, by [Reference Dotto, Moi and PatchkoriaDMP24, Theorem A], if
![]() $2$
is a unit in k, then
$2$
is a unit in k, then
![]() ${\mathrm {TCR}}(k;p)^{\phi \mathbb {Z}/2}=0$
for every prime p, so that we may assume that k has characteristic
${\mathrm {TCR}}(k;p)^{\phi \mathbb {Z}/2}=0$
for every prime p, so that we may assume that k has characteristic
![]() $2$
. Let
$2$
. Let
![]() $C_2$
act on
$C_2$
act on
![]() $k\otimes _Sk$
by swapping the two tensor factors, where
$k\otimes _Sk$
by swapping the two tensor factors, where
![]() $S\leq k$
is the subfield of squares. Let us denote by w the generator of
$S\leq k$
is the subfield of squares. Let us denote by w the generator of
![]() $C_2$
. The following is proved in Corollary 2.5.
$C_2$
. The following is proved in Corollary 2.5.
Theorem 2. Let k be a field of characteristic
![]() $2$
. For every integer
$2$
. For every integer
![]() $l\geq 0$
, there is an exact sequence
$l\geq 0$
, there is an exact sequence
where
![]() $\pi $
is the quotient map, and
$\pi $
is the quotient map, and
![]() $\phi $
is the ring homomorphism defined by
$\phi $
is the ring homomorphism defined by
![]() $\phi (a\otimes b)=ba^2\otimes b$
.
$\phi (a\otimes b)=ba^2\otimes b$
.
The map
![]() $\phi $
in fact determines an isomorphism
$\phi $
in fact determines an isomorphism
![]() $\phi \colon k\otimes _S k\to (k\otimes _S k)^{C_2}/Im(1+w)$
and is in a sense a replacement of the Frobenius of k when k is not perfect (see Lemma 2.1). It plays a crucial role in the calculations of §2.1 and in the description of
$\phi \colon k\otimes _S k\to (k\otimes _S k)^{C_2}/Im(1+w)$
and is in a sense a replacement of the Frobenius of k when k is not perfect (see Lemma 2.1). It plays a crucial role in the calculations of §2.1 and in the description of
![]() $J_{\langle 2^\bullet \rangle }$
.
$J_{\langle 2^\bullet \rangle }$
.
In [Reference KatoKat82, Theorem (1)], Kato exhibits a closely related exact sequence, involving the symmetric and quadratic Witt groups
![]() ${\mathrm {W}}^s(k)$
and
${\mathrm {W}}^s(k)$
and
![]() ${\mathrm {W}}^q(k)$
. Combined with Theorem 2, it gives isomorphisms
${\mathrm {W}}^q(k)$
. Combined with Theorem 2, it gives isomorphisms
for every
![]() $l\geq 0$
. In fact, this identifies the homotopy groups of
$l\geq 0$
. In fact, this identifies the homotopy groups of
![]() ${\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
with the genuine normal L-groups of k, as conjectured by Nikolaus, proved in great generality in [Reference Harpaz, Nikolaus and ShahHNS21], and verified in [Reference Dotto, Moi and PatchkoriaDMP24] in the case of perfect fields (see Remark 2.6).
${\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
with the genuine normal L-groups of k, as conjectured by Nikolaus, proved in great generality in [Reference Harpaz, Nikolaus and ShahHNS21], and verified in [Reference Dotto, Moi and PatchkoriaDMP24] in the case of perfect fields (see Remark 2.6).
From Theorem 2, we can also deduce a version of the Milnor conjecture for
![]() ${\mathrm {TC}}$
. Let us choose the respective equaliser and coequaliser
${\mathrm {TC}}$
. Let us choose the respective equaliser and coequaliser
as possible symbolic versions of topological cyclic homology modulo
![]() $2$
, where
$2$
, where
![]() ${\mathrm {W}}_{\langle 2^{\infty }\rangle }\Omega ^\ast _k$
is the limit over the map R of
${\mathrm {W}}_{\langle 2^{\infty }\rangle }\Omega ^\ast _k$
is the limit over the map R of
![]() ${\mathrm {W}}_{\langle 2^{\bullet }\rangle }\Omega ^\ast _k$
(and we are intentionally quotienting out
${\mathrm {W}}_{\langle 2^{\bullet }\rangle }\Omega ^\ast _k$
(and we are intentionally quotienting out
![]() $2$
before taking the equaliser). Now let
$2$
before taking the equaliser). Now let
be the kernel of the restriction map, where w is the involution on
![]() $\pi _0{\mathrm {TC}}(k;2)$
induced from the
$\pi _0{\mathrm {TC}}(k;2)$
induced from the
![]() $\mathbb {Z}/2$
-action on
$\mathbb {Z}/2$
-action on
![]() ${\mathrm {TCR}}(k;2)$
. Let us also denote
${\mathrm {TCR}}(k;2)$
. Let us also denote
![]() $T_{-1}:=\pi _{-1}{\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
, which we consider as a
$T_{-1}:=\pi _{-1}{\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
, which we consider as a
![]() $\pi _0{\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
-module. The following is a
$\pi _0{\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
-module. The following is a
![]() ${\mathrm {TC}}$
analogue of [Reference KatoKat82, Theorem (2)].
${\mathrm {TC}}$
analogue of [Reference KatoKat82, Theorem (2)].
Corollary 3. For every field k of characteristic
![]() $2$
, there is an isomorphism of graded rings
$2$
, there is an isomorphism of graded rings
and an isomorphism of graded
![]() $K^\ast /K^{\ast +1}$
-modules
$K^\ast /K^{\ast +1}$
-modules
We prove this result in §3.3. Our argument is fairly straightforward, but it relies on the Milnor conjecture at the prime
![]() $2$
and on the identification from [Reference Clausen, Mathew and MorrowCMM21, Proposition 2.26] of
$2$
and on the identification from [Reference Clausen, Mathew and MorrowCMM21, Proposition 2.26] of
![]() $\nu _{dRW/2}^\ast (k;2)$
and
$\nu _{dRW/2}^\ast (k;2)$
and
![]() $\epsilon _{dRW/2}^\ast (k;2)$
with the respective equaliser and coequaliser
$\epsilon _{dRW/2}^\ast (k;2)$
with the respective equaliser and coequaliser
of the projection
![]() $\pi $
and the inverse Cartier operator
$\pi $
and the inverse Cartier operator
![]() $C^{-1}$
. We then use Theorem 2 to compare K with the augmentation ideal I of the Witt group
$C^{-1}$
. We then use Theorem 2 to compare K with the augmentation ideal I of the Witt group
![]() ${\mathrm {W}}^s(k)$
. In order to carry out this last step, we need to understand the restriction map of
${\mathrm {W}}^s(k)$
. In order to carry out this last step, we need to understand the restriction map of
![]() $\pi _0{\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
. We are unable to do this directly, and we need to employ the existence of a trace map of
$\pi _0{\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
. We are unable to do this directly, and we need to employ the existence of a trace map of
![]() $\mathbb {Z}/2$
-equivariant spectra from the real algebraic K-theory spectrum
$\mathbb {Z}/2$
-equivariant spectra from the real algebraic K-theory spectrum
![]() ${\mathrm {tr}}\colon {\mathrm {KR}}(k)\to {\mathrm {TCR}}(k;2)$
, which lifts the K-theoretic trace of [Reference Bökstedt, Hsiang and MadsenBHM93] and which has a certain effect on
${\mathrm {tr}}\colon {\mathrm {KR}}(k)\to {\mathrm {TCR}}(k;2)$
, which lifts the K-theoretic trace of [Reference Bökstedt, Hsiang and MadsenBHM93] and which has a certain effect on
![]() $\pi _0$
. This map will appear in forthcoming work of Harpaz-Nikolaus-Shah [Reference Harpaz, Nikolaus and ShahHNS21] in the framework of real K-theory of Poincaré
$\pi _0$
. This map will appear in forthcoming work of Harpaz-Nikolaus-Shah [Reference Harpaz, Nikolaus and ShahHNS21] in the framework of real K-theory of Poincaré
![]() $\infty $
-categories. For completeness, we will give a construction in Appendix §A for rings with involution A by lifting the trace map of [Reference Dotto and OgleDO19] from
$\infty $
-categories. For completeness, we will give a construction in Appendix §A for rings with involution A by lifting the trace map of [Reference Dotto and OgleDO19] from
![]() ${\mathrm {THR}}(A)$
to
${\mathrm {THR}}(A)$
to
![]() ${\mathrm {TCR}}(A;p)$
.
${\mathrm {TCR}}(A;p)$
.
Theorem 4. Let A be a ring with involution. For every prime p, there is a map of
![]() $\mathbb {Z}/2$
-spectra
$\mathbb {Z}/2$
-spectra
![]() ${\mathrm {tr}}\colon {\mathrm {KR}}(A)\to {\mathrm {TCR}}(A;p)$
which forgets to the K-theoretic trace map of [Reference Bökstedt, Hsiang and MadsenBHM93]. The composite
${\mathrm {tr}}\colon {\mathrm {KR}}(A)\to {\mathrm {TCR}}(A;p)$
which forgets to the K-theoretic trace map of [Reference Bökstedt, Hsiang and MadsenBHM93]. The composite
sends the element of the Grothendieck-Witt group
![]() ${\mathrm {GW}}^s(A)$
represented by a symmetric form x on the free module
${\mathrm {GW}}^s(A)$
represented by a symmetric form x on the free module
![]() $A^{\oplus n}$
to
$A^{\oplus n}$
to
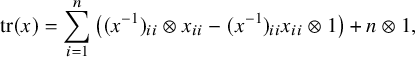 $$\begin{align*}{\mathrm{tr}}(x)=\sum_{i=1}^n\big((x^{-1})_{ii}\otimes x_{ii}-(x^{-1})_{ii}x_{ii}\otimes 1\big)+n\otimes 1, \end{align*}$$
$$\begin{align*}{\mathrm{tr}}(x)=\sum_{i=1}^n\big((x^{-1})_{ii}\otimes x_{ii}-(x^{-1})_{ii}x_{ii}\otimes 1\big)+n\otimes 1, \end{align*}$$
where
![]() $x_{ii}$
are the diagonal entries of the matrix of x for the standard basis of
$x_{ii}$
are the diagonal entries of the matrix of x for the standard basis of
![]() $A^{\oplus n}$
, and
$A^{\oplus n}$
, and
![]() $x^{-1}$
denotes the inverse matrix. Here, the isomorphism describing
$x^{-1}$
denotes the inverse matrix. Here, the isomorphism describing
![]() $\pi _0({\mathrm {THR}}(A)^{\mathbb {Z}/2})$
is from [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 5.1].
$\pi _0({\mathrm {THR}}(A)^{\mathbb {Z}/2})$
is from [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 5.1].
1 Preliminaries on real topological Hochschild homology
Here, we recall the basic definitions surrounding real topological cyclic homology. In order to streamline this section, we recast the definitions in the special case where the input is a discrete commutative ring A with the trivial involution (which in the next sections of the paper will be a field k of characteristic
![]() $2$
). We refer the details of these constructions to [Reference Dotto, Moi, Patchkoria and ReehDMPR21] and [Reference Dotto, Moi and PatchkoriaDMP24], and we will freely use the language of stable equivariant homotopy theory.
$2$
). We refer the details of these constructions to [Reference Dotto, Moi, Patchkoria and ReehDMPR21] and [Reference Dotto, Moi and PatchkoriaDMP24], and we will freely use the language of stable equivariant homotopy theory.
Let
![]() $O(2)$
be the infinite dihedral group that we identify with the semi-direct product
$O(2)$
be the infinite dihedral group that we identify with the semi-direct product
![]() $\mathbb {Z}/2\rtimes S^1$
by choosing the reflection across the real axis as the generator for
$\mathbb {Z}/2\rtimes S^1$
by choosing the reflection across the real axis as the generator for
![]() $\mathbb {Z}/2$
. The real topological Hochschild homology of A is a ring
$\mathbb {Z}/2$
. The real topological Hochschild homology of A is a ring
![]() $O(2)$
-spectrum
$O(2)$
-spectrum
![]() ${\mathrm {THR}}(A)$
, whose underlying ring
${\mathrm {THR}}(A)$
, whose underlying ring
![]() $S^1$
-spectrum is the topological Hochschild homology spectrum
$S^1$
-spectrum is the topological Hochschild homology spectrum
![]() ${\mathrm {THH}}(A)$
, originally defined in [Reference BökstedtBök86] (see also [Reference Bökstedt, Hsiang and MadsenBHM93] and [Reference Nikolaus and ScholzeNS18]). It can be constructed, as an
${\mathrm {THH}}(A)$
, originally defined in [Reference BökstedtBök86] (see also [Reference Bökstedt, Hsiang and MadsenBHM93] and [Reference Nikolaus and ScholzeNS18]). It can be constructed, as an
![]() $O(2)$
-equivariant ring orthogonal spectrum, as the geometric realisation of the dihedral bar construction
$O(2)$
-equivariant ring orthogonal spectrum, as the geometric realisation of the dihedral bar construction
where
![]() ${\mathrm {H}} A$
is (a flat model for) the Eilenberg-MacLane ring orthogonal
${\mathrm {H}} A$
is (a flat model for) the Eilenberg-MacLane ring orthogonal
![]() $\mathbb {Z}/2$
-spectrum of A, and
$\mathbb {Z}/2$
-spectrum of A, and
![]() $\otimes $
denotes the smash product of spectra (see [Reference Dotto, Moi, Patchkoria and ReehDMPR21]). The action of
$\otimes $
denotes the smash product of spectra (see [Reference Dotto, Moi, Patchkoria and ReehDMPR21]). The action of
![]() $O(2)$
is defined from the structure of a dihedral object in the sense of [Reference Fiedorowicz and LodayFL91, S 1.5, Example 5] and [Reference LodayLod87], where the cyclic group
$O(2)$
is defined from the structure of a dihedral object in the sense of [Reference Fiedorowicz and LodayFL91, S 1.5, Example 5] and [Reference LodayLod87], where the cyclic group
![]() $C_{n+1}$
acts in simplicial degree n by rotating the
$C_{n+1}$
acts in simplicial degree n by rotating the
![]() $n+1$
smash factors, and the reflection acts in degree n by reversing the order of the last n smash factors.
$n+1$
smash factors, and the reflection acts in degree n by reversing the order of the last n smash factors.
Now let p be a prime,
![]() $n\geq 0$
an integer, and
$n\geq 0$
an integer, and
![]() $D_{p^n}=\mathbb {Z}/2\rtimes C_{p^n}$
the finite dihedral subgroup of
$D_{p^n}=\mathbb {Z}/2\rtimes C_{p^n}$
the finite dihedral subgroup of
![]() $O(2)$
of order
$O(2)$
of order
![]() $2p^n$
. Since the Weyl group of
$2p^n$
. Since the Weyl group of
![]() $C_{p^n}$
inside
$C_{p^n}$
inside
![]() $D_{p^n}$
is
$D_{p^n}$
is
![]() $\mathbb {Z}/2$
, the (genuine) fixed-points ring spectrum
$\mathbb {Z}/2$
, the (genuine) fixed-points ring spectrum
![]() ${\mathrm {THR}}(A)^{C_{p^n}}$
is canonically a ring
${\mathrm {THR}}(A)^{C_{p^n}}$
is canonically a ring
![]() $\mathbb {Z}/2$
-spectrum. The inclusion of subgroups
$\mathbb {Z}/2$
-spectrum. The inclusion of subgroups
![]() $C_{p^{n-1}}\leq C_{p^n}$
induces a restriction map F, also called Frobenius, and a transfer map V, also called Verschiebung, which are maps of
$C_{p^{n-1}}\leq C_{p^n}$
induces a restriction map F, also called Frobenius, and a transfer map V, also called Verschiebung, which are maps of
![]() $\mathbb {Z}/2$
-spectra
$\mathbb {Z}/2$
-spectra
There is a further map R of
![]() $\mathbb {Z}/2$
-spectra, sometimes called restriction or truncation
$\mathbb {Z}/2$
-spectra, sometimes called restriction or truncation
which is defined from the real cyclotomic structure of
![]() ${\mathrm {THR}}(A)$
(see [Reference Dotto, Patchkoria and Jonsson MoiDPM22, Definition 3.9]). The maps R and F are moreover maps of ring spectra (see [Reference Dotto, Patchkoria and Jonsson MoiDPM22, Remark 3.10]). On underlying spectra, these are the maps
${\mathrm {THR}}(A)$
(see [Reference Dotto, Patchkoria and Jonsson MoiDPM22, Definition 3.9]). The maps R and F are moreover maps of ring spectra (see [Reference Dotto, Patchkoria and Jonsson MoiDPM22, Remark 3.10]). On underlying spectra, these are the maps
![]() $F, V$
and R of
$F, V$
and R of
![]() ${\mathrm {THH}}(A)$
, which after applying
${\mathrm {THH}}(A)$
, which after applying
![]() $\pi _0$
correspond to the operators on the ring of Witt vectors with the same name; see [Reference Hesselholt and MadsenHM97, Theorem 3.3].
$\pi _0$
correspond to the operators on the ring of Witt vectors with the same name; see [Reference Hesselholt and MadsenHM97, Theorem 3.3].
Definition 1.1. Let A be a commutative ring, and p a prime. The p-typical truncated real topological restriction homology, real topological restriction homology and real topological cyclic homology of A are the ring
![]() $\mathbb {Z}/2$
-spectra defined respectively as
$\mathbb {Z}/2$
-spectra defined respectively as

where the map F in the equaliser is induced by the Frobenius maps above, since R and F commute.
The
![]() $\mathbb {Z}/2$
-geometric fixed points of these spectra are characterised in [Reference Dotto, Moi and PatchkoriaDMP24], as we now recall. These results will be used in §2.1 below, and we encourage the reader, at least for the purpose of the present paper, to take them as definitions of these objects.
$\mathbb {Z}/2$
-geometric fixed points of these spectra are characterised in [Reference Dotto, Moi and PatchkoriaDMP24], as we now recall. These results will be used in §2.1 below, and we encourage the reader, at least for the purpose of the present paper, to take them as definitions of these objects.
In [Reference Dotto, Moi and PatchkoriaDMP24, §1.2], we give a canonical equivalence of ring spectra
where
![]() ${\mathrm {H}} {\underline {A}}$
is the Eilenberg MacLane spectrum of the
${\mathrm {H}} {\underline {A}}$
is the Eilenberg MacLane spectrum of the
![]() $\mathbb {Z}/2$
Mackey functor (or Tambara functor) with constant value A and transfer map
$\mathbb {Z}/2$
Mackey functor (or Tambara functor) with constant value A and transfer map
![]() $2$
. Its geometric fixed-points spectrum is then regarded as an
$2$
. Its geometric fixed-points spectrum is then regarded as an
![]() ${\mathrm {H}} A$
-module via the map of ring spectra
${\mathrm {H}} A$
-module via the map of ring spectra
where
![]() $N^{\mathbb {Z}/2}_e{\mathrm {H}} A$
is the Hill-Hopkins-Ravenel norm construction of the ring spectrum
$N^{\mathbb {Z}/2}_e{\mathrm {H}} A$
is the Hill-Hopkins-Ravenel norm construction of the ring spectrum
![]() ${\mathrm {H}} A$
of [Reference Hill, Hopkins and RavenelHHR16] and [Sto11], and
${\mathrm {H}} A$
of [Reference Hill, Hopkins and RavenelHHR16] and [Sto11], and
![]() $\epsilon $
is the counit of the free-forgetful adjunction between commutative ring
$\epsilon $
is the counit of the free-forgetful adjunction between commutative ring
![]() $\mathbb {Z}/2$
-spectra and commutative ring spectra. We will call this the Frobenius module structure of
$\mathbb {Z}/2$
-spectra and commutative ring spectra. We will call this the Frobenius module structure of
![]() $({\mathrm {H}} {\underline {A}})^{\phi \mathbb {Z}/2}$
, and refer to [Reference Dotto, Moi, Patchkoria and ReehDMPR21, §2.5] for the details of its construction. The Weyl group of
$({\mathrm {H}} {\underline {A}})^{\phi \mathbb {Z}/2}$
, and refer to [Reference Dotto, Moi, Patchkoria and ReehDMPR21, §2.5] for the details of its construction. The Weyl group of
![]() $\mathbb {Z}/2$
in
$\mathbb {Z}/2$
in
![]() $D_{2}=\mathbb {Z}/2\times C_2$
is
$D_{2}=\mathbb {Z}/2\times C_2$
is
![]() $C_2$
, and therefore,
$C_2$
, and therefore,
![]() ${\mathrm {THR}}(A)^{\phi \mathbb {Z}/2}$
is canonically a ring
${\mathrm {THR}}(A)^{\phi \mathbb {Z}/2}$
is canonically a ring
![]() $C_2$
-spectrum. In [Reference Dotto, Moi and PatchkoriaDMP24, Lemma 1.2], we lift the equivalence above to an equivalence of ring
$C_2$
-spectrum. In [Reference Dotto, Moi and PatchkoriaDMP24, Lemma 1.2], we lift the equivalence above to an equivalence of ring
![]() $C_2$
-spectra
$C_2$
-spectra
where the right factor is a module by applying the norm to the map
![]() ${\mathrm {H}} A\to ({\mathrm {H}} {\underline {A}})^{\phi \mathbb {Z}/2}$
, and the left factor is now regarded as a
${\mathrm {H}} A\to ({\mathrm {H}} {\underline {A}})^{\phi \mathbb {Z}/2}$
, and the left factor is now regarded as a
![]() $C_2$
-spectrum.
$C_2$
-spectrum.
This
![]() $C_2$
-equivariant homotopy type will help us characterise the
$C_2$
-equivariant homotopy type will help us characterise the
![]() $\mathbb {Z}/2$
-geometric fixed points of
$\mathbb {Z}/2$
-geometric fixed points of
![]() ${\mathrm {TRR}}^{n+1}(A;p)$
, inductively on n. For every
${\mathrm {TRR}}^{n+1}(A;p)$
, inductively on n. For every
![]() $n\geq 1$
, the
$n\geq 1$
, the
![]() $\mathbb {Z}/2$
-geometric fixed points of
$\mathbb {Z}/2$
-geometric fixed points of
![]() ${\mathrm {TRR}}^{n+1}(A;p)$
is equivalent to the product of
${\mathrm {TRR}}^{n+1}(A;p)$
is equivalent to the product of
![]() $(n+1)$
-copies of
$(n+1)$
-copies of
![]() ${\mathrm {THR}}(A)^{\phi \mathbb {Z}/2}$
if p is odd; see [Reference Dotto, Moi and PatchkoriaDMP24, Theorem 2.1]. For
${\mathrm {THR}}(A)^{\phi \mathbb {Z}/2}$
if p is odd; see [Reference Dotto, Moi and PatchkoriaDMP24, Theorem 2.1]. For
![]() $p=2$
, they are given by a pullback of ring spectra
$p=2$
, they are given by a pullback of ring spectra

see [Reference Dotto, Moi and PatchkoriaDMP24, Theorem 2.7]. Here,
![]() $\sigma _{n}$
is the generator of the Weyl group of
$\sigma _{n}$
is the generator of the Weyl group of
![]() $\mathbb {Z}/2$
inside the quotient
$\mathbb {Z}/2$
inside the quotient
![]() $D_{2^n}/C_{2^{n-1}}$
, which is also of order
$D_{2^n}/C_{2^{n-1}}$
, which is also of order
![]() $2$
. The map
$2$
. The map
is a certain canonical map, and r is the canonical map to the
![]() $C_2$
-geometric fixed points followed by the equivalence given by the cyclotomic structure (see above [Reference Dotto, Moi and PatchkoriaDMP24, Theorem 2.7] for the definitions).
$C_2$
-geometric fixed points followed by the equivalence given by the cyclotomic structure (see above [Reference Dotto, Moi and PatchkoriaDMP24, Theorem 2.7] for the definitions).
In [Reference Dotto, Moi and PatchkoriaDMP24, Theorem A], we also characterise the real topological cyclic homology of A by providing an equivalence of ring spectra
where f is the forgetful map.
Finally, we will need to briefly use the existence of norm maps on
![]() ${\mathrm {THR}}(A)$
in order calculate a certain restriction map, in Propositions 2.12 and 2.14. To establish their existence, we simply observe that the dihedral bar construction employed above to define
${\mathrm {THR}}(A)$
in order calculate a certain restriction map, in Propositions 2.12 and 2.14. To establish their existence, we simply observe that the dihedral bar construction employed above to define
![]() ${\mathrm {THR}}$
has a canonical symmetric monoidal structure, and therefore,
${\mathrm {THR}}$
has a canonical symmetric monoidal structure, and therefore,
![]() ${\mathrm {THR}}(A)$
is a strictly commutative
${\mathrm {THR}}(A)$
is a strictly commutative
![]() $O(2)$
-equivariant ring spectrum (provided we choose a strictly commutative and flat model for the Eilenberg-MacLane ring
$O(2)$
-equivariant ring spectrum (provided we choose a strictly commutative and flat model for the Eilenberg-MacLane ring
![]() $C_2$
-spectrum
$C_2$
-spectrum
![]() ${\mathrm {H}} {\underline {A}}$
, which we can achieve by a cofibrant replacement in the flat model structure of [Sto11, Reference Brun, Dundas and StolzBDS16]). Thus, we obtain non-additive norm maps
${\mathrm {H}} {\underline {A}}$
, which we can achieve by a cofibrant replacement in the flat model structure of [Sto11, Reference Brun, Dundas and StolzBDS16]). Thus, we obtain non-additive norm maps
for every pair of finite subgroups
![]() $H\leq G\leq O(2)$
, which, when composed with a restriction map, satisfy the multiplicative double-coset formula.
$H\leq G\leq O(2)$
, which, when composed with a restriction map, satisfy the multiplicative double-coset formula.
2 Real TR and real TC of fields of characteristic
 $2$
$2$
2.1 The geometric fixed points of TRR and TCR for fields of characteristic
 $2$
$2$
Let k be a field of characteristic
![]() $2$
, and
$2$
, and
![]() $S\leq k$
the subfield of squares. We regard k as an S-vector space and endow the abelian group
$S\leq k$
the subfield of squares. We regard k as an S-vector space and endow the abelian group
![]() $k\otimes _Sk$
with the involution w which flips the two tensor factors.
$k\otimes _Sk$
with the involution w which flips the two tensor factors.
The homotopy groups of
![]() ${\mathrm {TRR}}(k)^{\phi \mathbb {Z}/2}$
have been computed in [Reference Dotto, Moi and PatchkoriaDMP24, Theorem 4.7, Corollary 4.8] when the field k is perfect, as a sum of copies of k. In this section, we give an analogous description of these homotopy groups for a general field of characteristic
${\mathrm {TRR}}(k)^{\phi \mathbb {Z}/2}$
have been computed in [Reference Dotto, Moi and PatchkoriaDMP24, Theorem 4.7, Corollary 4.8] when the field k is perfect, as a sum of copies of k. In this section, we give an analogous description of these homotopy groups for a general field of characteristic
![]() $2$
(and an analogous proof), where some of the copies of k appearing in the calculation for perfect fields are replaced by expressions involving
$2$
(and an analogous proof), where some of the copies of k appearing in the calculation for perfect fields are replaced by expressions involving
![]() $k\otimes _S k$
(which is isomorphic to k if k is perfect). This is Theorem 2.7 below, and its statement and proof will be the content of §2.1.
$k\otimes _S k$
(which is isomorphic to k if k is perfect). This is Theorem 2.7 below, and its statement and proof will be the content of §2.1.
The key algebraic input for extending the calculation to non-perfect fields lies in the following Lemma, which we will use several times throughout the paper. For every elementary tensor
![]() $a\otimes b\in k\otimes _Sk$
, let us define
$a\otimes b\in k\otimes _Sk$
, let us define
where the
![]() $C_2$
-invariants on the right are with respect to the involution w. We note that this map does not obviously extend to
$C_2$
-invariants on the right are with respect to the involution w. We note that this map does not obviously extend to
![]() $k\otimes _Sk$
, as it is unclear how to define it on a sum of elementary tensors. It will serve as a replacement of the Frobenius of k and will be related to the cyclotomic structure of
$k\otimes _Sk$
, as it is unclear how to define it on a sum of elementary tensors. It will serve as a replacement of the Frobenius of k and will be related to the cyclotomic structure of
![]() ${\mathrm {THR}}(k)$
by Proposition 2.4 and to the fibre sequence of [Reference KatoKat82, Theorem (1)] describing the Witt groups of k in Remark 2.6.
${\mathrm {THR}}(k)$
by Proposition 2.4 and to the fibre sequence of [Reference KatoKat82, Theorem (1)] describing the Witt groups of k in Remark 2.6.
Lemma 2.1. The assignment
![]() $\phi $
induces a well-defined additive isomorphism
$\phi $
induces a well-defined additive isomorphism
![]() $k\otimes _Sk\xrightarrow {\cong }(k\otimes _Sk)^{C_2}/Im(1+w)$
. This isomorphism moreover fits into a commutative diagram
$k\otimes _Sk\xrightarrow {\cong }(k\otimes _Sk)^{C_2}/Im(1+w)$
. This isomorphism moreover fits into a commutative diagram
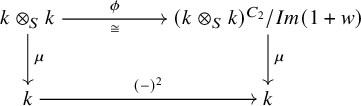
where the map
![]() $\mu $
is the multiplication map, which is an isomorphism if and only if k is perfect.
$\mu $
is the multiplication map, which is an isomorphism if and only if k is perfect.
Proof. It is easy to see that
![]() $\phi $
extends to a well-defined additive map after we quotient the image of
$\phi $
extends to a well-defined additive map after we quotient the image of
![]() $1+w$
in the target. To see that it is an isomorphism, choose a basis
$1+w$
in the target. To see that it is an isomorphism, choose a basis
![]() $k\cong \oplus _XS$
of k as an S-vector space. This induces an isomorphism of
$k\cong \oplus _XS$
of k as an S-vector space. This induces an isomorphism of
![]() $C_2$
-equivariant abelian groups
$C_2$
-equivariant abelian groups
where the involution on the right-hand side sends a basis element
![]() $(x, y)$
of
$(x, y)$
of
![]() $X\times X$
to
$X\times X$
to
![]() $(y, x)$
. Under this isomorphism, the map
$(y, x)$
. Under this isomorphism, the map
![]() $\phi $
corresponds to the map
$\phi $
corresponds to the map
where the second isomorphism is the sum over X of the isomorphism
![]() $k\cong \oplus _XS$
, and the last isomorphism sends the summand x to the summand
$k\cong \oplus _XS$
, and the last isomorphism sends the summand x to the summand
![]() $(x, x)$
via the square map
$(x, x)$
via the square map
![]() $(-)^2\colon k\xrightarrow {\cong }S$
.
$(-)^2\colon k\xrightarrow {\cong }S$
.
We calculate the homotopy groups of
![]() ${\mathrm {TRR}}(k;2)^{\phi \mathbb {Z}/2}$
using the iterated pullback description of [Reference Dotto, Moi and PatchkoriaDMP24, Theorem 2.7], reviewed in §1. This description relies on the
${\mathrm {TRR}}(k;2)^{\phi \mathbb {Z}/2}$
using the iterated pullback description of [Reference Dotto, Moi and PatchkoriaDMP24, Theorem 2.7], reviewed in §1. This description relies on the
![]() $C_2$
-equivariant homotopy type of
$C_2$
-equivariant homotopy type of
![]() ${\mathrm {THR}}(k)^{{\phi \mathbb {Z}/2}}$
, which we calculate in Proposition 2.3 below using Lemma 2.1 and the following decomposition of the geometric fixed points
${\mathrm {THR}}(k)^{{\phi \mathbb {Z}/2}}$
, which we calculate in Proposition 2.3 below using Lemma 2.1 and the following decomposition of the geometric fixed points
![]() ${\mathrm {H}} \underline {k}^{\phi \mathbb {Z}/2}$
.
${\mathrm {H}} \underline {k}^{\phi \mathbb {Z}/2}$
.
Lemma 2.2. Let k be a field of characteristic
![]() $2$
, and let us equip
$2$
, and let us equip
![]() ${\mathrm {H}} \underline {k}^{\phi \mathbb {Z}/2}$
with the Frobenius module structure of §1. Then there is a natural splitting of k-modules
${\mathrm {H}} \underline {k}^{\phi \mathbb {Z}/2}$
with the Frobenius module structure of §1. Then there is a natural splitting of k-modules
where
![]() $\varphi =(-)^2\colon k\to k$
denotes the Frobenius homomorphism of k.
$\varphi =(-)^2\colon k\to k$
denotes the Frobenius homomorphism of k.
Proof. Since k is a field, the Frobenius module structure on
![]() $\underline {k}^{{\phi \mathbb {Z}/2}}$
provides an equivalence of k-modules
$\underline {k}^{{\phi \mathbb {Z}/2}}$
provides an equivalence of k-modules
Since the Frobenius module structure on
![]() ${\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}$
comes from a k-algebra
${\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}$
comes from a k-algebra
![]() ${\mathrm {H}} k\to {\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}$
, the action of k on
${\mathrm {H}} k\to {\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}$
, the action of k on
![]() $\pi _n({\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}})$
is obtained by restricting, along the ring map
$\pi _n({\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}})$
is obtained by restricting, along the ring map
![]() $k=\pi _0{\mathrm {H}} k\to \pi _0({\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}})$
, the action of
$k=\pi _0{\mathrm {H}} k\to \pi _0({\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}})$
, the action of
![]() $\pi _0({\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}})$
on
$\pi _0({\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}})$
on
![]() $\pi _n({\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}})$
induced by the ring structure of
$\pi _n({\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}})$
induced by the ring structure of
![]() ${\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}$
. The
${\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}$
. The
![]() $\pi _0({\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}})$
-module
$\pi _0({\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}})$
-module
![]() $\pi _n({\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}})$
can be computed from the isotropy separation sequence as follows. The canonical ring homomorphism
$\pi _n({\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}})$
can be computed from the isotropy separation sequence as follows. The canonical ring homomorphism
![]() ${\mathrm {H}} k={\mathrm {H}}\underline {k}^{\mathbb {Z}/2}\to {\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}$
induces a long exact sequence of k-modules
${\mathrm {H}} k={\mathrm {H}}\underline {k}^{\mathbb {Z}/2}\to {\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}$
induces a long exact sequence of k-modules
Since
![]() $\pi _n{\mathrm {H}} k=0$
for
$\pi _n{\mathrm {H}} k=0$
for
![]() $n>0$
and since the transfer map
$n>0$
and since the transfer map
![]() $k=k_{\mathbb {Z}/2}\cong \pi _{0}{\mathrm {H}} k_{h \mathbb {Z}/2}\to \pi _{0}{\mathrm {H}} k=k$
is multiplication by
$k=k_{\mathbb {Z}/2}\cong \pi _{0}{\mathrm {H}} k_{h \mathbb {Z}/2}\to \pi _{0}{\mathrm {H}} k=k$
is multiplication by
![]() $2$
and hence also zero, all the connecting homomorphisms are isomorphisms of k-modules
$2$
and hence also zero, all the connecting homomorphisms are isomorphisms of k-modules
![]() $\pi _n {\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}\cong \pi _{n-1}{\mathrm {H}} k_{h \mathbb {Z}/2}$
for
$\pi _n {\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}\cong \pi _{n-1}{\mathrm {H}} k_{h \mathbb {Z}/2}$
for
![]() $n>0$
. The homotopy groups of the homotopy-orbit spectra are equivalent to group-cohomology, and since k is of characteristic
$n>0$
. The homotopy groups of the homotopy-orbit spectra are equivalent to group-cohomology, and since k is of characteristic
![]() $2$
, the standard resolution
$2$
, the standard resolution
gives an isomorphism of k-modules
![]() $\pi _{n-1}{\mathrm {H}} k_{h \mathbb {Z}/2}\cong H^{n-1}(\mathbb {Z}/2;k)\cong k$
for every
$\pi _{n-1}{\mathrm {H}} k_{h \mathbb {Z}/2}\cong H^{n-1}(\mathbb {Z}/2;k)\cong k$
for every
![]() $n>0$
. Moreover, again because the transfer map is zero, the canonical map
$n>0$
. Moreover, again because the transfer map is zero, the canonical map
![]() $k=\pi _0 {\mathrm {H}} k\to \pi _0 {\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}$
is an isomorphism of rings. Thus, we have completely identified the
$k=\pi _0 {\mathrm {H}} k\to \pi _0 {\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}$
is an isomorphism of rings. Thus, we have completely identified the
![]() $\pi _0 {\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}$
-module structure of
$\pi _0 {\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}$
-module structure of
![]() $\pi _n {\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}$
.
$\pi _n {\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}$
.
It finally remains to show that under the isomorphism
![]() $k\cong \pi _0 {\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}$
above, the ring map
$k\cong \pi _0 {\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}$
above, the ring map
![]() ${{\mathrm {H}} k\to {\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}}$
defining the Frobenius module structure induces the Frobenius
${{\mathrm {H}} k\to {\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}}$
defining the Frobenius module structure induces the Frobenius
![]() $\varphi $
in
$\varphi $
in
![]() $\pi _0$
. This follows either from identifying this map with the Tate-valued Frobenius (see [Reference Nikolaus and ScholzeNS18, Example IV.1.2. (i)]) or by the following direct calculation. The counit
$\pi _0$
. This follows either from identifying this map with the Tate-valued Frobenius (see [Reference Nikolaus and ScholzeNS18, Example IV.1.2. (i)]) or by the following direct calculation. The counit
![]() $\epsilon \colon N^{\mathbb {Z}/2}_e({\mathrm {H}} k)\to {\mathrm {H}}\underline {k}$
induces a map on isotropy separation sequences
$\epsilon \colon N^{\mathbb {Z}/2}_e({\mathrm {H}} k)\to {\mathrm {H}}\underline {k}$
induces a map on isotropy separation sequences
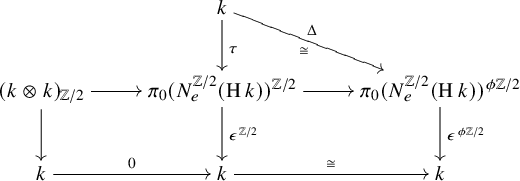
where the map
![]() $\tau $
is the external norm map. We need to identify the composite
$\tau $
is the external norm map. We need to identify the composite
![]() $\epsilon ^{\mathbb {Z}/2}\tau $
of the two vertical maps in the middle column. This is the norm of the constant Tambara functor
$\epsilon ^{\mathbb {Z}/2}\tau $
of the two vertical maps in the middle column. This is the norm of the constant Tambara functor
![]() $\underline {k}$
associated to the commutative ring k, and it is therefore the Frobenius
$\underline {k}$
associated to the commutative ring k, and it is therefore the Frobenius
![]() $\varphi $
(see also [Reference Dotto, Krause, Nikolaus and PatchkoriaDKNP23, Example 2.18] for an explicit identification of the target of
$\varphi $
(see also [Reference Dotto, Krause, Nikolaus and PatchkoriaDKNP23, Example 2.18] for an explicit identification of the target of
![]() $\tau $
).
$\tau $
).
We denote by
![]() ${\mathrm {H}}(k\otimes _Sk, w)$
the
${\mathrm {H}}(k\otimes _Sk, w)$
the
![]() $C_2$
-equivariant Eilenberg-MacLane spectrum of the abelian group
$C_2$
-equivariant Eilenberg-MacLane spectrum of the abelian group
![]() $k\otimes _Sk$
with
$k\otimes _Sk$
with
![]() $C_2$
-action w which switches the tensor factors.
$C_2$
-action w which switches the tensor factors.
Proposition 2.3. Let k be a field of characteristic
![]() $2$
. Then there is a natural equivalence of
$2$
. Then there is a natural equivalence of
![]() $C_2$
-equivariant spectra
$C_2$
-equivariant spectra
 $$\begin{align*}{{\mathrm{THR}}(k)}^{{\phi \mathbb{Z}/2}}\simeq \bigoplus_{n \geq 0} \Sigma^{n\rho} {\mathrm{H}}(k\otimes_Sk, w) \oplus \bigoplus_{ \begin{smallmatrix} (n, m) \\ 0 \leq n < m \end{smallmatrix}} \Sigma^{n+m} {C_2}_{+} \otimes {\mathrm{H}}(k\otimes_Sk), \end{align*}$$
$$\begin{align*}{{\mathrm{THR}}(k)}^{{\phi \mathbb{Z}/2}}\simeq \bigoplus_{n \geq 0} \Sigma^{n\rho} {\mathrm{H}}(k\otimes_Sk, w) \oplus \bigoplus_{ \begin{smallmatrix} (n, m) \\ 0 \leq n < m \end{smallmatrix}} \Sigma^{n+m} {C_2}_{+} \otimes {\mathrm{H}}(k\otimes_Sk), \end{align*}$$
where
![]() $\rho $
is the regular representation of
$\rho $
is the regular representation of
![]() $C_2$
. It follows that there is a natural equivalence of spectra
$C_2$
. It follows that there is a natural equivalence of spectra
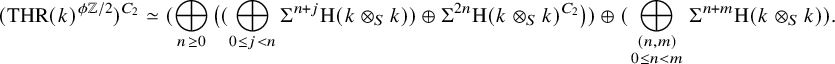 $$\begin{align*}({{\mathrm{THR}}(k)}^{{\phi \mathbb{Z}/2}})^{C_2}\simeq (\bigoplus_{n \geq 0} \big((\bigoplus_{0 \leq j < n} \Sigma^{n+j} {\mathrm{H}}(k\otimes_S k))\oplus \Sigma^{2n} {\mathrm{H}}(k\otimes_Sk)^{C_2}\big)) \oplus (\bigoplus_{\begin{smallmatrix} (n, m) \\ 0 \leq n < m \end{smallmatrix}} \Sigma^{n+m} {\mathrm{H}}(k\otimes_Sk)). \end{align*}$$
$$\begin{align*}({{\mathrm{THR}}(k)}^{{\phi \mathbb{Z}/2}})^{C_2}\simeq (\bigoplus_{n \geq 0} \big((\bigoplus_{0 \leq j < n} \Sigma^{n+j} {\mathrm{H}}(k\otimes_S k))\oplus \Sigma^{2n} {\mathrm{H}}(k\otimes_Sk)^{C_2}\big)) \oplus (\bigoplus_{\begin{smallmatrix} (n, m) \\ 0 \leq n < m \end{smallmatrix}} \Sigma^{n+m} {\mathrm{H}}(k\otimes_Sk)). \end{align*}$$
Proof. Let
![]() ${\mathrm {H}}\underline {k}$
be the Eilenberg MacLane
${\mathrm {H}}\underline {k}$
be the Eilenberg MacLane
![]() $C_2$
-spectrum of the ring with trivial involution k. Using the splitting of Lemma 2.2, we obtain from [Reference Dotto, Moi and PatchkoriaDMP24, Lemma 4.3] an equivalence of
$C_2$
-spectrum of the ring with trivial involution k. Using the splitting of Lemma 2.2, we obtain from [Reference Dotto, Moi and PatchkoriaDMP24, Lemma 4.3] an equivalence of
![]() $C_2$
-spectra
$C_2$
-spectra
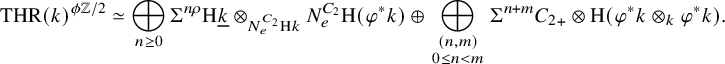 $$\begin{align*}{{\mathrm{THR}}(k)}^{{\phi \mathbb{Z}/2}}\simeq \bigoplus_{n \geq 0} \Sigma^{n\rho} {\mathrm{H}}\underline{k}\otimes_{N_{e}^{C_2}{\mathrm{H}} k}N_{e}^{C_2}{\mathrm{H}}(\varphi^\ast k) \oplus \bigoplus_{ \begin{smallmatrix} (n, m) \\ 0 \leq n < m \end{smallmatrix}} \Sigma^{n+m} {C_2}_{+} \otimes {\mathrm{H}}(\varphi^\ast k\otimes_k\varphi^\ast k).\end{align*}$$
$$\begin{align*}{{\mathrm{THR}}(k)}^{{\phi \mathbb{Z}/2}}\simeq \bigoplus_{n \geq 0} \Sigma^{n\rho} {\mathrm{H}}\underline{k}\otimes_{N_{e}^{C_2}{\mathrm{H}} k}N_{e}^{C_2}{\mathrm{H}}(\varphi^\ast k) \oplus \bigoplus_{ \begin{smallmatrix} (n, m) \\ 0 \leq n < m \end{smallmatrix}} \Sigma^{n+m} {C_2}_{+} \otimes {\mathrm{H}}(\varphi^\ast k\otimes_k\varphi^\ast k).\end{align*}$$
This equivalence is moreover natural in k since the decomposition of
![]() ${\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}$
of Lemma 2.2 is natural. Clearly,
${\mathrm {H}}\underline {k}^{{\phi \mathbb {Z}/2}}$
of Lemma 2.2 is natural. Clearly,
![]() $\varphi ^\ast k\otimes _k\varphi ^\ast k=k\otimes _S k$
, and therefore, to obtain the first decomposition of the proposition, it is sufficient to show that the canonical map
$\varphi ^\ast k\otimes _k\varphi ^\ast k=k\otimes _S k$
, and therefore, to obtain the first decomposition of the proposition, it is sufficient to show that the canonical map
is an equivalence, where the middle term is
![]() $\pi _0$
of the underlying spectrum of the left term, with the induced involution.
$\pi _0$
of the underlying spectrum of the left term, with the induced involution.
Let us choose a basis of the k-vector space
![]() $\varphi ^\ast k$
; that is, we write
$\varphi ^\ast k$
; that is, we write
![]() $\varphi ^\ast k$
as a direct sum
$\varphi ^\ast k$
as a direct sum
over some set X. Since the norm commutes with direct sums, we obtain an equivalence of
![]() $C_2$
-spectra
$C_2$
-spectra
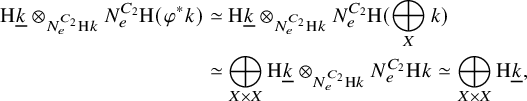 $$ \begin{align*} {\mathrm{H}}\underline{k}\otimes_{N_{e}^{C_2}{\mathrm{H}} k}N_{e}^{C_2}{\mathrm{H}}(\varphi^\ast k)&\simeq {\mathrm{H}}\underline{k}\otimes_{N_{e}^{C_2}{\mathrm{H}} k}N_{e}^{C_2}{\mathrm{H}}(\bigoplus_{X}k) \\&\simeq \bigoplus_{X\times X} {\mathrm{H}}\underline{k}\otimes_{N_{e}^{C_2}{\mathrm{H}} k}N_{e}^{C_2}{\mathrm{H}} k\simeq \bigoplus_{X\times X} {\mathrm{H}}\underline{k}, \end{align*} $$
$$ \begin{align*} {\mathrm{H}}\underline{k}\otimes_{N_{e}^{C_2}{\mathrm{H}} k}N_{e}^{C_2}{\mathrm{H}}(\varphi^\ast k)&\simeq {\mathrm{H}}\underline{k}\otimes_{N_{e}^{C_2}{\mathrm{H}} k}N_{e}^{C_2}{\mathrm{H}}(\bigoplus_{X}k) \\&\simeq \bigoplus_{X\times X} {\mathrm{H}}\underline{k}\otimes_{N_{e}^{C_2}{\mathrm{H}} k}N_{e}^{C_2}{\mathrm{H}} k\simeq \bigoplus_{X\times X} {\mathrm{H}}\underline{k}, \end{align*} $$
where the last term is the indexed sum of
![]() ${\mathrm {H}}\underline {k}$
with the involution on
${\mathrm {H}}\underline {k}$
with the involution on
![]() $X\times X$
that swaps the product factors. Under this equivalence, the canonical map above corresponds to the equivalence
$X\times X$
that swaps the product factors. Under this equivalence, the canonical map above corresponds to the equivalence
where the middle equivalence is the tensor product of two copies of the choice of basis above.
Now let us identify the
![]() $C_2$
-fixed points of
$C_2$
-fixed points of
![]() ${{\mathrm {THR}}(k)}^{{\phi \mathbb {Z}/2}}$
. Notice that
${{\mathrm {THR}}(k)}^{{\phi \mathbb {Z}/2}}$
. Notice that
![]() ${\mathrm {H}}(k\otimes _Sk, w) $
is a module over
${\mathrm {H}}(k\otimes _Sk, w) $
is a module over
![]() ${\mathrm {H}}\underline {k}$
(via the ring map
${\mathrm {H}}\underline {k}$
(via the ring map
![]() $k\to k\otimes _Sk$
that sends a to
$k\to k\otimes _Sk$
that sends a to
![]() $a^2\otimes 1$
), and therefore, its
$a^2\otimes 1$
), and therefore, its
![]() $C_2$
-fixed-points spectrum is an
$C_2$
-fixed-points spectrum is an
![]() ${\mathrm {H}} k$
-module. Therefore, it decomposes canonically as a wedge of Eilenberg-MacLane spectra. Its homotopy groups are isomorphic to the Bredon homology groups
${\mathrm {H}} k$
-module. Therefore, it decomposes canonically as a wedge of Eilenberg-MacLane spectra. Its homotopy groups are isomorphic to the Bredon homology groups
which in turn are the homology groups of the chain complex
where the first nonzero group on the left is in degree n and the last nonzero group on the right is in degree
![]() $2n$
(notice that all the signs on the arrows are
$2n$
(notice that all the signs on the arrows are
![]() $+$
since k has characteristic
$+$
since k has characteristic
![]() $2$
). It follows that all the groups below n and above
$2$
). It follows that all the groups below n and above
![]() $2n$
vanish, that
$2n$
vanish, that
and that
for every
![]() $n\leq i<2n$
, where the left-pointing isomorphism is the map
$n\leq i<2n$
, where the left-pointing isomorphism is the map
![]() $\phi $
from Lemma 2.1.
$\phi $
from Lemma 2.1.
In order to calculate the homotopy groups of
![]() ${\mathrm {TRR}}(k;2)^{\phi \mathbb {Z}/2}$
and
${\mathrm {TRR}}(k;2)^{\phi \mathbb {Z}/2}$
and
![]() ${\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
, we also need to determine the maps r and f (see §1), under the equivalences of Proposition 2.3. In the following proposition, the summands are arranged exactly as in Proposition 2.3. In particular, the summands indexed on
${\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
, we also need to determine the maps r and f (see §1), under the equivalences of Proposition 2.3. In the following proposition, the summands are arranged exactly as in Proposition 2.3. In particular, the summands indexed on
![]() $(n, m)$
with
$(n, m)$
with
![]() $n<m$
in the source, and those indexed on
$n<m$
in the source, and those indexed on
![]() $(n, m)$
with
$(n, m)$
with
![]() $n \neq m$
in the target, correspond to the induced summands.
$n \neq m$
in the target, correspond to the induced summands.
Proposition 2.4. For any field k of characteristic
![]() $2$
, the maps
$2$
, the maps
![]() $r, f \colon {({{\mathrm {THR}}(k)}^{{\phi \mathbb {Z}/2}})}^{C_2} \to {{\mathrm {THR}}(k)}^{{\phi \mathbb {Z}/2}}$
induce on
$r, f \colon {({{\mathrm {THR}}(k)}^{{\phi \mathbb {Z}/2}})}^{C_2} \to {{\mathrm {THR}}(k)}^{{\phi \mathbb {Z}/2}}$
induce on
![]() $\pi _\ast $
the maps
$\pi _\ast $
the maps
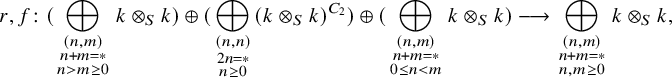 $$\begin{align*}r, f\colon (\bigoplus_{ \begin{smallmatrix}(n, m) \\ n+m=\ast \\ n>m\geq 0 \end{smallmatrix}} k\otimes_S k ) \oplus (\bigoplus_{\begin{smallmatrix} (n, n)\\ 2n=\ast \\ n \geq 0 \end{smallmatrix}} (k\otimes_S k )^{C_2} ) \oplus (\bigoplus_{\begin{smallmatrix}(n, m) \\ n+m=\ast \\ 0\leq n<m \end{smallmatrix}} k\otimes_S k ) \longrightarrow \bigoplus_{\begin{smallmatrix}(n, m)\\ n+m=\ast\\ n, m \geq 0\end{smallmatrix}} k\otimes_S k, \end{align*}$$
$$\begin{align*}r, f\colon (\bigoplus_{ \begin{smallmatrix}(n, m) \\ n+m=\ast \\ n>m\geq 0 \end{smallmatrix}} k\otimes_S k ) \oplus (\bigoplus_{\begin{smallmatrix} (n, n)\\ 2n=\ast \\ n \geq 0 \end{smallmatrix}} (k\otimes_S k )^{C_2} ) \oplus (\bigoplus_{\begin{smallmatrix}(n, m) \\ n+m=\ast \\ 0\leq n<m \end{smallmatrix}} k\otimes_S k ) \longrightarrow \bigoplus_{\begin{smallmatrix}(n, m)\\ n+m=\ast\\ n, m \geq 0\end{smallmatrix}} k\otimes_S k, \end{align*}$$
where r kills the
![]() $(n, m)$
-summands with
$(n, m)$
-summands with
![]() $n<m$
, maps the
$n<m$
, maps the
![]() $(n, m)$
-summands with
$(n, m)$
-summands with
![]() $n>m$
to the
$n>m$
to the
![]() $(n, m)$
-summand via the identity, and maps the
$(n, m)$
-summand via the identity, and maps the
![]() $(n, n)$
-summand to the
$(n, n)$
-summand to the
![]() $(n, n)$
-summand via the composite
$(n, n)$
-summand via the composite
of the quotient map and the isomorphism of Lemma 2.1. The map f kills the
![]() $(n, m)$
-summands with
$(n, m)$
-summands with
![]() $n>m$
, is the fixed-points inclusion on the summand
$n>m$
, is the fixed-points inclusion on the summand
![]() $(n, n)$
, and embeds diagonally the
$(n, n)$
, and embeds diagonally the
![]() $(n, m)$
-summands with
$(n, m)$
-summands with
![]() $n<m$
into the sum of the summands
$n<m$
into the sum of the summands
![]() $(n, m)$
and
$(n, m)$
and
![]() $(m, n)$
.
$(m, n)$
.
Proof. By [Reference Dotto, Moi and PatchkoriaDMP24, Lemma 4.3], the map r vanishes on the summands
![]() $(n, m)$
with
$(n, m)$
with
![]() $n<m$
. By the same lemma, under the identification of Proposition 2.3, it is given on the other summands, for a fixed
$n<m$
. By the same lemma, under the identification of Proposition 2.3, it is given on the other summands, for a fixed
![]() $n\geq 0$
, by the outer composite of the maps in the diagram
$n\geq 0$
, by the outer composite of the maps in the diagram
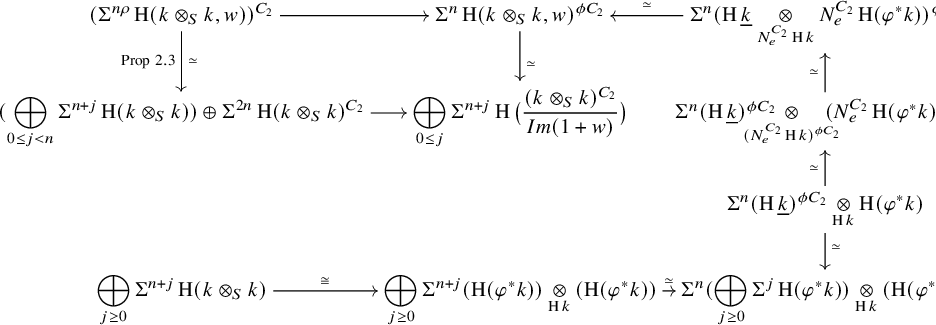
Here, the left map on the top row is the canonical map, and the right map on the top row is the equivalence of the proof of Proposition 2.3. In the right column, the top vertical map is the monoidality of the geometric fixed points, the second map is the diagonal equivalence, and the third one is the splitting induced by the Frobenius module structure. The two bottom horizontal maps are the canonical equivalences.
Let us now consider the top left square. Its right vertical equivalence is given by splitting
![]() ${\mathrm {H}}(k\otimes _Sk, w)^{\phi C_2}$
as the sum of its homotopy groups using the
${\mathrm {H}}(k\otimes _Sk, w)^{\phi C_2}$
as the sum of its homotopy groups using the
![]() ${\mathrm {H}} k$
-module induced by the map
${\mathrm {H}} k$
-module induced by the map
![]() $k\to k\otimes _Sk$
as we did in Proposition 2.3 for
$k\to k\otimes _Sk$
as we did in Proposition 2.3 for
![]() ${\mathrm {H}}(k\otimes _Sk, w)^{C_2}$
, and then by identifying these homotopy groups with the homology of the chain complex
${\mathrm {H}}(k\otimes _Sk, w)^{C_2}$
, and then by identifying these homotopy groups with the homology of the chain complex
where the first nonzero group on the left is in degree zero. The horizontal map on the second row sends the summand
![]() $j<n$
to the summand j via
$j<n$
to the summand j via
![]() $\phi $
, and it maps the last summand to the summand
$\phi $
, and it maps the last summand to the summand
![]() $j=2n$
via the projection map (here,
$j=2n$
via the projection map (here,
![]() $\phi $
appears because we used it to identify the homotopy groups of the source of the map in the proof of Proposition 2.3). The square commutes by the naturality of the canonical map from fixed points to geometric fixed points.
$\phi $
appears because we used it to identify the homotopy groups of the source of the map in the proof of Proposition 2.3). The square commutes by the naturality of the canonical map from fixed points to geometric fixed points.
Thus, the identification of the map r follows once we prove that the equivalence from the bottom left corner of the diagram to the second entry of the second row is the map
![]() $\phi $
on homotopy groups. Let
$\phi $
on homotopy groups. Let
![]() $a, b\colon \mathbb {S}\to {\mathrm {H}} k$
, so that the suspension of
$a, b\colon \mathbb {S}\to {\mathrm {H}} k$
, so that the suspension of
![]() $a\otimes b\colon \mathbb {S}\to {\mathrm {H}}(k\otimes _S k)$
is a generator of a homotopy group of the bottom left entry of the diagram. The composite of the equivalences up to the top right corner of the diagram sends
$a\otimes b\colon \mathbb {S}\to {\mathrm {H}}(k\otimes _S k)$
is a generator of a homotopy group of the bottom left entry of the diagram. The composite of the equivalences up to the top right corner of the diagram sends
![]() $a\otimes b$
to the element of the homotopy group represented by
$a\otimes b$
to the element of the homotopy group represented by
![]() $a\otimes N_e^{C_2}(b)$
. The remaining two equivalences send this to the element represented by
$a\otimes N_e^{C_2}(b)$
. The remaining two equivalences send this to the element represented by
![]() $b\cdot a\otimes b$
, where the multiplication is with respect to the k-module action on
$b\cdot a\otimes b$
, where the multiplication is with respect to the k-module action on
![]() $\varphi ^\ast k$
, and this is precisely
$\varphi ^\ast k$
, and this is precisely
![]() $ba^2\otimes b=\phi (a\otimes b)$
.
$ba^2\otimes b=\phi (a\otimes b)$
.
The identification of f is simpler: by [Reference Dotto, Moi and PatchkoriaDMP24, Lemma 4.3], it is the diagonal on the summands
![]() $(n, m)$
with
$(n, m)$
with
![]() $n<m$
. The identification on the other summands follows from the fact that the restriction map
$n<m$
. The identification on the other summands follows from the fact that the restriction map
is the inclusion of fixed points in degree
![]() $*=2n$
, and zero otherwise.
$*=2n$
, and zero otherwise.
Corollary 2.5. For every field k of characteristic
![]() $2$
, and every integer
$2$
, and every integer
![]() $l\geq 0$
, there is an exact sequence
$l\geq 0$
, there is an exact sequence
where
![]() $\pi $
quotients the image of
$\pi $
quotients the image of
![]() $1+w$
, and
$1+w$
, and
![]() $\phi $
is the isomorphism of Lemma 2.1 restricted to the fixed points. By Kato’s calculation [Reference KatoKat82, Theorem (1)], this identifies
$\phi $
is the isomorphism of Lemma 2.1 restricted to the fixed points. By Kato’s calculation [Reference KatoKat82, Theorem (1)], this identifies
![]() $\pi _{2l} {\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
with the symmetric Witt group of k, and
$\pi _{2l} {\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
with the symmetric Witt group of k, and
![]() $\pi _{2l-1} {\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
with the quadratic Witt group of k.
$\pi _{2l-1} {\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
with the quadratic Witt group of k.
Proof. By Proposition 2.4, the map
![]() $r-f$
is an isomorphism in
$r-f$
is an isomorphism in
![]() $\pi _\ast $
when restricted and corestricted to the summands
$\pi _\ast $
when restricted and corestricted to the summands
![]() $(n, m)$
with
$(n, m)$
with
![]() $n\neq m$
. It is therefore an isomorphism in odd degrees, and its long exact sequence decomposes into exact sequences
$n\neq m$
. It is therefore an isomorphism in odd degrees, and its long exact sequence decomposes into exact sequences
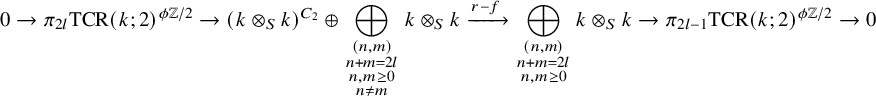 $$\begin{align*}0\to\pi_{2l} {\mathrm{TCR}}(k;2)^{\phi\mathbb{Z}/2}\to (k\otimes_S k)^{C_2}\oplus\bigoplus_{\begin{smallmatrix}(n, m)\\ n+m=2l \\ n, m \geq 0\\ n\neq m\end{smallmatrix}} k\otimes_S k\xrightarrow{r-f} \bigoplus_{\begin{smallmatrix}(n, m)\\ n+m=2l\\ n, m \geq 0\end{smallmatrix}} k\otimes_S k\to \pi_{2l-1} {\mathrm{TCR}}(k;2)^{\phi\mathbb{Z}/2}\to 0 \end{align*}$$
$$\begin{align*}0\to\pi_{2l} {\mathrm{TCR}}(k;2)^{\phi\mathbb{Z}/2}\to (k\otimes_S k)^{C_2}\oplus\bigoplus_{\begin{smallmatrix}(n, m)\\ n+m=2l \\ n, m \geq 0\\ n\neq m\end{smallmatrix}} k\otimes_S k\xrightarrow{r-f} \bigoplus_{\begin{smallmatrix}(n, m)\\ n+m=2l\\ n, m \geq 0\end{smallmatrix}} k\otimes_S k\to \pi_{2l-1} {\mathrm{TCR}}(k;2)^{\phi\mathbb{Z}/2}\to 0 \end{align*}$$
for every
![]() $l\geq 0$
. Again by Proposition 2.4, the kernel and cokernel of
$l\geq 0$
. Again by Proposition 2.4, the kernel and cokernel of
![]() $r-f$
are the same as those of
$r-f$
are the same as those of
where
![]() $\iota $
is the fixed-points inclusion. These are respectively isomorphic to the kernel and cokernel of
$\iota $
is the fixed-points inclusion. These are respectively isomorphic to the kernel and cokernel of
![]() $\pi -\phi $
, by applying the isomorphism
$\pi -\phi $
, by applying the isomorphism
![]() $\phi $
of Lemma 2.1 to the target.
$\phi $
of Lemma 2.1 to the target.
In [Reference KatoKat82], Kato exhibits an exact sequence
where
![]() ${\mathrm {W}}^s(k)$
and
${\mathrm {W}}^s(k)$
and
![]() ${\mathrm {W}}^q(k)$
are respectively the symmetric and quadratic Witt groups of k. It is easy to see that the kernel and cokernel of
${\mathrm {W}}^q(k)$
are respectively the symmetric and quadratic Witt groups of k. It is easy to see that the kernel and cokernel of
![]() $\pi -\phi $
agree with those above, by restricting and corestricting the maps to the fixed points.
$\pi -\phi $
agree with those above, by restricting and corestricting the maps to the fixed points.
Remark 2.6. Corollary 2.5 in particular shows that the homotopy groups of the spectrum
![]() ${\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
agree with the homotopy groups of the cofibre
${\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
agree with the homotopy groups of the cofibre
![]() ${\mathrm {L}}^n(k)$
of the canonical map
${\mathrm {L}}^n(k)$
of the canonical map
induced by the symmetrisation map from the quadratic to the genuine Poincaré structure, as defined in [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and SteimleCDH+23, Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and SteimleCDH+20a, Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and SteimleCDH+20b]. This confirms a conjecture of Nikolaus, proved in [Reference Harpaz, Nikolaus and ShahHNS21], in the case of fields. This is because the even and odd homotopy groups of
![]() ${\mathrm {L}}^n(k)$
, in degrees greater or equal to
${\mathrm {L}}^n(k)$
, in degrees greater or equal to
![]() $-1$
, are respectively the Witt groups of symmetric and quadratic forms of k, as explained in [Reference Dotto, Moi and PatchkoriaDMP24, Remark 4.6].
$-1$
, are respectively the Witt groups of symmetric and quadratic forms of k, as explained in [Reference Dotto, Moi and PatchkoriaDMP24, Remark 4.6].
Let us denote by
![]() $\pi \colon (k\otimes _Sk)^{C_2}\to (k\otimes _Sk)^{C_2}/Im(1+w)$
the projection map, so that for every
$\pi \colon (k\otimes _Sk)^{C_2}\to (k\otimes _Sk)^{C_2}/Im(1+w)$
the projection map, so that for every
![]() $x\in (k\otimes _Sk)^{C_2}$
, we can consider the element
$x\in (k\otimes _Sk)^{C_2}$
, we can consider the element
![]() $(\phi ^{-1}\pi )(x)$
of
$(\phi ^{-1}\pi )(x)$
of
![]() $k\otimes _S k$
. For every
$k\otimes _S k$
. For every
![]() $n\geq 0$
, we define a subgroup of
$n\geq 0$
, we define a subgroup of
![]() $(k\otimes _S k)^{C_2}$
by
$(k\otimes _S k)^{C_2}$
by
where by convention,
![]() $\phi ^{0}((k\otimes _S k)^{C_2})=(k\otimes _S k)^{C_2}$
. Thus, by construction, there is a well-defined map
$\phi ^{0}((k\otimes _S k)^{C_2})=(k\otimes _S k)^{C_2}$
. Thus, by construction, there is a well-defined map
for every
![]() $n\geq 1$
, and a map
$n\geq 1$
, and a map
![]() $ (\phi ^{-1}\pi )^{n+1}\colon \phi ^{n}\big ((k\otimes _S k)^{C_2}\big )\to k\otimes _S k$
. Let us consider the pullback
$ (\phi ^{-1}\pi )^{n+1}\colon \phi ^{n}\big ((k\otimes _S k)^{C_2}\big )\to k\otimes _S k$
. Let us consider the pullback
where we keep in mind that one of the two maps which we pull back is composed with the involution w of
![]() $k\otimes _S k$
.
$k\otimes _S k$
.
Theorem 2.7. Let k be a field of characteristic
![]() $2$
. For any
$2$
. For any
![]() $l \geq 1$
, there is an isomorphism
$l \geq 1$
, there is an isomorphism
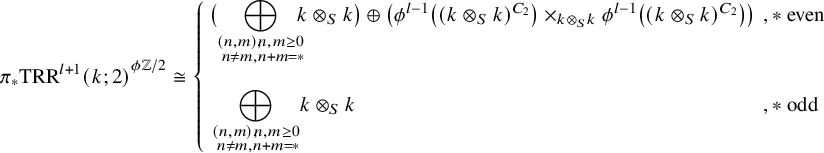 $$\begin{align*}\pi_\ast {{\mathrm{TRR}}^{l+1}(k;2)}^{{\phi \mathbb{Z}/2}} \cong \left\{ \begin{array}{ll}\displaystyle \big(\!\!\bigoplus_{\begin{smallmatrix} (n, m), &\!\!\!\!n, m \geq 0 \\ n\neq m, &\!\!\!\! n+m=\ast \end{smallmatrix}}\!\!\!\! k\otimes_S k\big)\oplus \big( \phi^{l-1}\big((k\otimes_S k)^{C_2}\big)\times_{k\otimes_S k}\phi^{l-1}\big((k\otimes_S k)^{C_2}\big) \big) &, \ast\ \mbox{even} \\ \\ \displaystyle \bigoplus_{\begin{smallmatrix} (n, m), &\!\!\!\!n, m \geq 0 \\ n\neq m, &\!\!\!\! n+m=\ast \end{smallmatrix}}\!\! k\otimes_S k &, \ast\ \mbox{odd} \end{array} \right. \end{align*}$$
$$\begin{align*}\pi_\ast {{\mathrm{TRR}}^{l+1}(k;2)}^{{\phi \mathbb{Z}/2}} \cong \left\{ \begin{array}{ll}\displaystyle \big(\!\!\bigoplus_{\begin{smallmatrix} (n, m), &\!\!\!\!n, m \geq 0 \\ n\neq m, &\!\!\!\! n+m=\ast \end{smallmatrix}}\!\!\!\! k\otimes_S k\big)\oplus \big( \phi^{l-1}\big((k\otimes_S k)^{C_2}\big)\times_{k\otimes_S k}\phi^{l-1}\big((k\otimes_S k)^{C_2}\big) \big) &, \ast\ \mbox{even} \\ \\ \displaystyle \bigoplus_{\begin{smallmatrix} (n, m), &\!\!\!\!n, m \geq 0 \\ n\neq m, &\!\!\!\! n+m=\ast \end{smallmatrix}}\!\! k\otimes_S k &, \ast\ \mbox{odd} \end{array} \right. \end{align*}$$
In particular, in degree zero, we obtain a ring isomorphism
The maps
![]() $R, F \colon {{\mathrm {TRR}}^{l+1}(k;2)}^{{\phi \mathbb {Z}/2}} \to {{\mathrm {TRR}}^{l}(k;2)}^{{\phi \mathbb {Z}/2}}$
and the Weyl action are described on homotopy groups as follows.
$R, F \colon {{\mathrm {TRR}}^{l+1}(k;2)}^{{\phi \mathbb {Z}/2}} \to {{\mathrm {TRR}}^{l}(k;2)}^{{\phi \mathbb {Z}/2}}$
and the Weyl action are described on homotopy groups as follows.
The map R kills the
![]() $(n, m)$
-summands with
$(n, m)$
-summands with
![]() $n \neq m$
, and in even degrees, it sends an element
$n \neq m$
, and in even degrees, it sends an element
![]() $(x, y)$
of the right-hand pullback to
$(x, y)$
of the right-hand pullback to
![]() $(\phi ^{-1}\pi (x), \phi ^{-1}\pi (y))$
.
$(\phi ^{-1}\pi (x), \phi ^{-1}\pi (y))$
.
The map F kills the
![]() $(n, m)$
-summands with
$(n, m)$
-summands with
![]() $m<n$
, embeds the
$m<n$
, embeds the
![]() $(n, m)$
-summands with
$(n, m)$
-summands with
![]() $n<m$
diagonally into the sum of the
$n<m$
diagonally into the sum of the
![]() $(n, m)$
and
$(n, m)$
and
![]() $(m, n)$
-summands, and in even degrees, it sends an element
$(m, n)$
-summands, and in even degrees, it sends an element
![]() $(x, y)$
of the right-hand pullback to
$(x, y)$
of the right-hand pullback to
![]() $(x, x)$
.
$(x, x)$
.
The Weyl action swaps the
![]() $(n, m)$
-summand and the
$(n, m)$
-summand and the
![]() $(m, n)$
-summand for all
$(m, n)$
-summand for all
![]() $n\neq m$
, and in even degrees takes an element
$n\neq m$
, and in even degrees takes an element
![]() $(x, y)$
in the pullback to
$(x, y)$
in the pullback to
![]() $(y, x)$
.
$(y, x)$
.
Proof. By [Reference Dotto, Moi and PatchkoriaDMP24, Theorem 2.7] and §1, for every
![]() $l\geq 1$
, there is a pullback square of ring spectra
$l\geq 1$
, there is a pullback square of ring spectra

where
![]() $\sigma _l$
denotes the action of the generator of the Weyl group of
$\sigma _l$
denotes the action of the generator of the Weyl group of
![]() $\mathbb {Z}/2$
in
$\mathbb {Z}/2$
in
![]() $D_{2^{l}}/C_{2^{l-1}}$
, which is of order
$D_{2^{l}}/C_{2^{l-1}}$
, which is of order
![]() $2$
. We prove, by induction on l, that the connecting homomorphism in the Mayer-Vietoris long exact sequence of this pullback square vanish, and therefore that the square gives a pullback square of homotopy groups. One can see, again by induction, that these pullbacks of homotopy groups indeed match the description of the homotopy groups of the Theorem. However, we will need to prove the vanishing of the connecting maps and the explicit description of the pullback in the same induction step.
$2$
. We prove, by induction on l, that the connecting homomorphism in the Mayer-Vietoris long exact sequence of this pullback square vanish, and therefore that the square gives a pullback square of homotopy groups. One can see, again by induction, that these pullbacks of homotopy groups indeed match the description of the homotopy groups of the Theorem. However, we will need to prove the vanishing of the connecting maps and the explicit description of the pullback in the same induction step.
For
![]() $l=1$
, the pullback above describing
$l=1$
, the pullback above describing
![]() ${{\mathrm {TRR}}^2(k;2)}^{{\phi \mathbb {Z}/2}}$
is equivalent to the pullback
${{\mathrm {TRR}}^2(k;2)}^{{\phi \mathbb {Z}/2}}$
is equivalent to the pullback
along the maps r and
![]() $\sigma _1 r$
(since the right vertical map in the square above is the diagonal for
$\sigma _1 r$
(since the right vertical map in the square above is the diagonal for
![]() $l=1$
). By the characterisation of r of Proposition 2.4, the map
$l=1$
). By the characterisation of r of Proposition 2.4, the map
![]() $r-\sigma _1r$
in the corresponding Mayer-Vietoris sequence is surjective in every degree. Therefore, there is a pullback
$r-\sigma _1r$
in the corresponding Mayer-Vietoris sequence is surjective in every degree. Therefore, there is a pullback
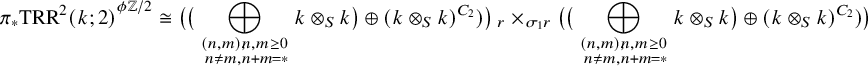 $$\begin{align*}\pi_\ast {{\mathrm{TRR}}^2(k;2)}^{{\phi \mathbb{Z}/2}}\cong \big(\big(\bigoplus_{\begin{smallmatrix} (n, m), &\!\!\!\!n, m \geq 0 \\ n\neq m, &\!\!\!\! n+m=\ast \end{smallmatrix}} k\otimes_S k\big)\oplus (k\otimes_S k)^{C_2})\big) \ {}_{r}\times_{\sigma_1 r} \big(\big(\bigoplus_{\begin{smallmatrix} (n, m), &\!\!\!\!n, m \geq 0 \\ n\neq m, &\!\!\!\! n+m=\ast \end{smallmatrix}} k\otimes_S k\big)\oplus (k\otimes_S k)^{C_2})\big) \end{align*}$$
$$\begin{align*}\pi_\ast {{\mathrm{TRR}}^2(k;2)}^{{\phi \mathbb{Z}/2}}\cong \big(\big(\bigoplus_{\begin{smallmatrix} (n, m), &\!\!\!\!n, m \geq 0 \\ n\neq m, &\!\!\!\! n+m=\ast \end{smallmatrix}} k\otimes_S k\big)\oplus (k\otimes_S k)^{C_2})\big) \ {}_{r}\times_{\sigma_1 r} \big(\big(\bigoplus_{\begin{smallmatrix} (n, m), &\!\!\!\!n, m \geq 0 \\ n\neq m, &\!\!\!\! n+m=\ast \end{smallmatrix}} k\otimes_S k\big)\oplus (k\otimes_S k)^{C_2})\big) \end{align*}$$
in even degrees and an analogous pullback without the summands
![]() $(k\otimes _S k)^{C_2}$
in odd degrees. Here, the subscripts of the product indicate which maps we are pulling back along. By the description of r from Proposition 2.4, this is isomorphic to the pullback of the statement of the Theorem. The characterisation of the maps
$(k\otimes _S k)^{C_2}$
in odd degrees. Here, the subscripts of the product indicate which maps we are pulling back along. By the description of r from Proposition 2.4, this is isomorphic to the pullback of the statement of the Theorem. The characterisation of the maps
![]() $R, F$
and of the Weyl action follows by the description of the corresponding maps of [Reference Dotto, Moi and PatchkoriaDMP24, Theorem 2.7].
$R, F$
and of the Weyl action follows by the description of the corresponding maps of [Reference Dotto, Moi and PatchkoriaDMP24, Theorem 2.7].
Now let
![]() $l \geq 2$
, and suppose that the decomposition above holds for
$l \geq 2$
, and suppose that the decomposition above holds for
![]() $\pi _\ast {{\mathrm {TRR}}^h(k;2)}^{{\phi \mathbb {Z}/2}}$
for all
$\pi _\ast {{\mathrm {TRR}}^h(k;2)}^{{\phi \mathbb {Z}/2}}$
for all
![]() $h \leq l$
, and that the maps
$h \leq l$
, and that the maps
![]() $R, F\colon {{\mathrm {TRR}}^{h}(k;2)}^{{\phi \mathbb {Z}/2}}\to {{\mathrm {TRR}}^{h-1}(k;2)}^{{\phi \mathbb {Z}/2}}$
and
$R, F\colon {{\mathrm {TRR}}^{h}(k;2)}^{{\phi \mathbb {Z}/2}}\to {{\mathrm {TRR}}^{h-1}(k;2)}^{{\phi \mathbb {Z}/2}}$
and
![]() $\sigma _h$
are given in homotopy groups by the formulas of the Theorem. We will show that the same holds for
$\sigma _h$
are given in homotopy groups by the formulas of the Theorem. We will show that the same holds for
![]() $l+1$
. The Mayer-Vietoris sequence of the pullback square above is then (we recall that
$l+1$
. The Mayer-Vietoris sequence of the pullback square above is then (we recall that
![]() $\sigma _1F =F$
)
$\sigma _1F =F$
)

for
![]() $\ast $
even, and a similar expression without the fixed points terms for
$\ast $
even, and a similar expression without the fixed points terms for
![]() $\ast $
odd. An argument completely analogous to that of the proof of [Reference Dotto, Moi and PatchkoriaDMP24, Theorem 4.7] shows that the bottom vertical map is surjective and identifies its kernel with the formula of the Theorem. The description of the maps R and F also follows by a similar argument.
$\ast $
odd. An argument completely analogous to that of the proof of [Reference Dotto, Moi and PatchkoriaDMP24, Theorem 4.7] shows that the bottom vertical map is surjective and identifies its kernel with the formula of the Theorem. The description of the maps R and F also follows by a similar argument.
Remark 2.8. From the proof of Theorem 2.7, we see that the isomorphism for the
![]() $0$
-th homotopy group is explicitly given by the map
$0$
-th homotopy group is explicitly given by the map
where we implicitly identify the target
![]() $\pi _0 {{\mathrm {THR}}(k;2)}^{{\phi \mathbb {Z}/2}}$
of
$\pi _0 {{\mathrm {THR}}(k;2)}^{{\phi \mathbb {Z}/2}}$
of
![]() $F^l$
with
$F^l$
with
![]() $k\otimes _Sk$
, and
$k\otimes _Sk$
, and
![]() $\sigma :=\sigma _l$
denotes the Weyl action on the source of this map. We can see this directly as follows. Let us express the source of this map as the iterated pullback
$\sigma :=\sigma _l$
denotes the Weyl action on the source of this map. We can see this directly as follows. Let us express the source of this map as the iterated pullback
as in [Reference Dotto, Moi and PatchkoriaDMP24, Remark 2.8], where the pullback has
![]() $2l$
factors, and the isomorphism is given by the map
$2l$
factors, and the isomorphism is given by the map
![]() $(F^l, F^{l-1}R, F^{l-2}R^2, \dots , F R^{l-1}, F\sigma R^{l-1}, \dots , F^{l-2}\sigma R^2, F^{l-1}\sigma R, F^{l}\sigma )$
. We still have a pullback after applying
$(F^l, F^{l-1}R, F^{l-2}R^2, \dots , F R^{l-1}, F\sigma R^{l-1}, \dots , F^{l-2}\sigma R^2, F^{l-1}\sigma R, F^{l}\sigma )$
. We still have a pullback after applying
![]() $\pi _0$
because the connecting maps of the Mayer-Vietoris sequences vanish as seen in the proof of Theorem 2.7. By Proposition 2.4,
$\pi _0$
because the connecting maps of the Mayer-Vietoris sequences vanish as seen in the proof of Theorem 2.7. By Proposition 2.4,
![]() $r=\phi ^{-1}\pi $
and f is the fixed points inclusion
$r=\phi ^{-1}\pi $
and f is the fixed points inclusion
![]() $(k\otimes _S k)^{C_2}\to k\otimes _S k$
. Since f is injective, the projection onto the first and last factors defines an isomorphism between this pullback and
$(k\otimes _S k)^{C_2}\to k\otimes _S k$
. Since f is injective, the projection onto the first and last factors defines an isomorphism between this pullback and
![]() $\phi ^{l-1}\big ((k\otimes _S k)^{C_2}\big )\times _{k\otimes _S k}\phi ^{l-1}\big ((k\otimes _S k)^{C_2}\big )$
, and the composite map is indeed
$\phi ^{l-1}\big ((k\otimes _S k)^{C_2}\big )\times _{k\otimes _S k}\phi ^{l-1}\big ((k\otimes _S k)^{C_2}\big )$
, and the composite map is indeed
![]() $(F^l, F^l\sigma )$
.
$(F^l, F^l\sigma )$
.
2.2 The canonical generators of TRR
We recall that for every commutative ring R, the ring of
![]() $2$
-typical
$2$
-typical
![]() $(n+1)$
-truncated Witt vectors
$(n+1)$
-truncated Witt vectors
![]() ${\mathrm {W}}_{\langle 2^{n}\rangle }(R)$
is the set
${\mathrm {W}}_{\langle 2^{n}\rangle }(R)$
is the set
![]() $R^{\times n+1}$
equipped with the unique functorial ring structure which makes the Witt polynomials into ring homomorphisms (see, for example, [Reference HesselholtHes15, §1]). Additively, it is generated by the elements
$R^{\times n+1}$
equipped with the unique functorial ring structure which makes the Witt polynomials into ring homomorphisms (see, for example, [Reference HesselholtHes15, §1]). Additively, it is generated by the elements
where the entry a is in the
![]() $(n-i+1)$
-st component, a ranges through the elements of R and
$(n-i+1)$
-st component, a ranges through the elements of R and
![]() $i=0, \dots , n$
.
$i=0, \dots , n$
.
The goal of this section is to define canonical generators for the pullback of Theorem 2.7, analogous to the generators
![]() $V^{n-i}\tau _i(a)$
of the
$V^{n-i}\tau _i(a)$
of the
![]() $(n+1)$
-truncated Witt vectors, thus providing generators for
$(n+1)$
-truncated Witt vectors, thus providing generators for
![]() $\pi _0 {{\mathrm {TRR}}^{n+1}(k;2)}^{\phi \mathbb {Z}/2}$
analogous to those of
$\pi _0 {{\mathrm {TRR}}^{n+1}(k;2)}^{\phi \mathbb {Z}/2}$
analogous to those of
![]() ${\mathrm {W}}_{\langle 2^{n}\rangle }(k)$
.
${\mathrm {W}}_{\langle 2^{n}\rangle }(k)$
.
Recall that for every elementary tensor
![]() $a\otimes b\in k\otimes _S k$
, we have defined
$a\otimes b\in k\otimes _S k$
, we have defined
(see Lemma 2.1). Similarly, for any elementary tensor
![]() $a\otimes b\in k\otimes _S k$
and
$a\otimes b\in k\otimes _S k$
and
![]() $n\geq 0$
, let us iterate this construction and define
$n\geq 0$
, let us iterate this construction and define
as well as
![]() $\tau _0(a\otimes b):=a\otimes b\in k\otimes _S k$
. We will show in Proposition 2.9 that
$\tau _0(a\otimes b):=a\otimes b\in k\otimes _S k$
. We will show in Proposition 2.9 that
![]() $\phi ^n(a\otimes b)$
indeed belongs to
$\phi ^n(a\otimes b)$
indeed belongs to
![]() $\phi ^{n-1}\big ((k\otimes _S k)^{C_2}\big )$
, and as a consequence, the pairs defined by
$\phi ^{n-1}\big ((k\otimes _S k)^{C_2}\big )$
, and as a consequence, the pairs defined by
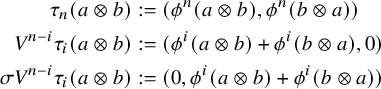 $$ \begin{align*} \tau_n(a\otimes b)&:=(\phi^n(a\otimes b), \phi^n(b\otimes a)) \\ V^{n-i}\tau_i(a\otimes b)&:=(\phi^i(a\otimes b)+\phi^i(b\otimes a), 0)\\ \sigma V^{n-i}\tau_i(a\otimes b)&:=(0, \phi^i(a\otimes b)+\phi^i(b\otimes a)) \end{align*} $$
$$ \begin{align*} \tau_n(a\otimes b)&:=(\phi^n(a\otimes b), \phi^n(b\otimes a)) \\ V^{n-i}\tau_i(a\otimes b)&:=(\phi^i(a\otimes b)+\phi^i(b\otimes a), 0)\\ \sigma V^{n-i}\tau_i(a\otimes b)&:=(0, \phi^i(a\otimes b)+\phi^i(b\otimes a)) \end{align*} $$
for every
![]() $0\leq i<n$
belong to the pullback
$0\leq i<n$
belong to the pullback
![]() $\phi ^{n-1}((k\otimes _S k)^{C_2})\underset {k\otimes _S k}{\times }\phi ^{n-1}((k\otimes _S k)^{C_2})$
. Here, we recall that the pullback is taken with respect to the maps
$\phi ^{n-1}((k\otimes _S k)^{C_2})\underset {k\otimes _S k}{\times }\phi ^{n-1}((k\otimes _S k)^{C_2})$
. Here, we recall that the pullback is taken with respect to the maps
![]() $(\phi ^{-1}\pi )^n$
and
$(\phi ^{-1}\pi )^n$
and
![]() $w(\phi ^{-1}\pi )^n$
(see the diagram above Theorem 2.7), and
$w(\phi ^{-1}\pi )^n$
(see the diagram above Theorem 2.7), and
![]() $\sigma $
is the Weyl action which switches the two pullback components.
$\sigma $
is the Weyl action which switches the two pullback components.
Proposition 2.9. Let k be a field of characteristic
![]() $2$
. For every
$2$
. For every
![]() $n\geq 0$
, the subgroup
$n\geq 0$
, the subgroup
![]() $\phi ^{n}\big ((k\otimes _S k)^{C_2}\big )$
of
$\phi ^{n}\big ((k\otimes _S k)^{C_2}\big )$
of
![]() $k\otimes _Sk$
is generated by elements of the form
$k\otimes _Sk$
is generated by elements of the form
![]() $\phi ^{n+1}(a\otimes b)$
and
$\phi ^{n+1}(a\otimes b)$
and
![]() $\phi ^{i}(a\otimes b)+\phi ^i(b\otimes a)$
, for
$\phi ^{i}(a\otimes b)+\phi ^i(b\otimes a)$
, for
![]() $0\leq i\leq n$
and
$0\leq i\leq n$
and
![]() $a\otimes b\in k\otimes _S k$
.
$a\otimes b\in k\otimes _S k$
.
It follows that, for every
![]() $n\geq 1$
,
$n\geq 1$
,
is generated by the elements
![]() $\tau _n(a\otimes b)$
,
$\tau _n(a\otimes b)$
,
![]() $V^{n-i}\tau _i(a\otimes b)$
and
$V^{n-i}\tau _i(a\otimes b)$
and
![]() $\sigma V^{n-i}\tau _i(a\otimes b)$
, for
$\sigma V^{n-i}\tau _i(a\otimes b)$
, for
![]() $0\leq i\leq n-1$
and
$0\leq i\leq n-1$
and
![]() $a\otimes b\in k\otimes _Sk$
.
$a\otimes b\in k\otimes _Sk$
.
Proof. Let us first show that the proposed generators belong to
![]() $\phi ^{n}\big ((k\otimes _S k)^{C_2}\big )$
. For the first, we see that for every
$\phi ^{n}\big ((k\otimes _S k)^{C_2}\big )$
. For the first, we see that for every
![]() $1\leq j\leq n$
, we have that
$1\leq j\leq n$
, we have that
which belongs to
![]() $(k\otimes _S k)^{C_2}$
since
$(k\otimes _S k)^{C_2}$
since
![]() $n+1-j\geq 1$
. However, for all
$n+1-j\geq 1$
. However, for all
![]() $0\leq i\leq n-1$
, we have that
$0\leq i\leq n-1$
, we have that
if
![]() $0\leq j\leq i$
, which is a fixed point, and for
$0\leq j\leq i$
, which is a fixed point, and for
![]() $i<j\leq n$
, this is
$i<j\leq n$
, this is
since
![]() $\pi $
quotients off the image of
$\pi $
quotients off the image of
![]() $1+w$
.
$1+w$
.
The proof that these elements generate
![]() $\phi ^{n}\big ((k\otimes _S k)^{C_2}\big )$
is by induction on n. For
$\phi ^{n}\big ((k\otimes _S k)^{C_2}\big )$
is by induction on n. For
![]() $n=0$
, consider the exact sequence
$n=0$
, consider the exact sequence
By Lemma 2.1, the right term is generated by the equivalence classes of the elements of the form
![]() $\phi (a\otimes b)$
, and the image of
$\phi (a\otimes b)$
, and the image of
![]() $1+w$
is generated by the elements of the form
$1+w$
is generated by the elements of the form
![]() $a\otimes b+b\otimes a$
, which proves the claim.
$a\otimes b+b\otimes a$
, which proves the claim.
Now suppose that the claim holds for
![]() $n-1$
, and consider the exact sequence
$n-1$
, and consider the exact sequence
By an argument analogous to the proof of Lemma 2.1,
![]() $\phi $
defines an isomorphism between
$\phi $
defines an isomorphism between
![]() $\phi ^{n-1}((k\otimes _S k)^{C_2})$
and
$\phi ^{n-1}((k\otimes _S k)^{C_2})$
and
![]() $\phi ^{n}((k\otimes _S k)^{C_2})/Im(1+w)$
. Thus, by the inductive assumption, the classes of
$\phi ^{n}((k\otimes _S k)^{C_2})/Im(1+w)$
. Thus, by the inductive assumption, the classes of
![]() $\phi ^{n+1}(a\otimes b)$
and
$\phi ^{n+1}(a\otimes b)$
and
![]() $\phi ^{i}(a\otimes b)+\phi ^i(b\otimes a)$
, for
$\phi ^{i}(a\otimes b)+\phi ^i(b\otimes a)$
, for
![]() $1\leq i\leq n$
and
$1\leq i\leq n$
and
![]() $a\otimes b\in k\otimes _S k$
, generate the quotient. The image of
$a\otimes b\in k\otimes _S k$
, generate the quotient. The image of
![]() $1+w$
is generated by the elements of the form
$1+w$
is generated by the elements of the form
![]() $a\otimes b+b\otimes a$
, which concludes the induction.
$a\otimes b+b\otimes a$
, which concludes the induction.
The proof for
![]() $\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
is completely analogous, by induction on the exact sequences
$\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
is completely analogous, by induction on the exact sequences
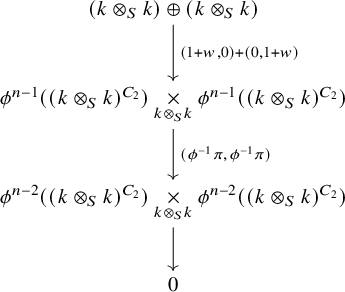
Next, we want to understand the effect of the transfer and norm maps of
![]() ${\mathrm {TRR}}(k)$
under the isomorphism of Theorem 2.7, and their relation to the generators of Proposition 2.9. For every
${\mathrm {TRR}}(k)$
under the isomorphism of Theorem 2.7, and their relation to the generators of Proposition 2.9. For every
![]() $0\leq h<l$
, let
$0\leq h<l$
, let
be the transfer map associated to the subgroup inclusion
![]() $D_{2^h}\leq D_{2^{l}}$
.
$D_{2^h}\leq D_{2^{l}}$
.
Proposition 2.10. For every
![]() $0< h<l$
, the map
$0< h<l$
, the map
![]() ${\mathrm {tran}}^{D_{2^l}}_{D_{2^{h}}}$
corresponds, under the isomorphism of Theorem 2.7, to the group homomorphism
${\mathrm {tran}}^{D_{2^l}}_{D_{2^{h}}}$
corresponds, under the isomorphism of Theorem 2.7, to the group homomorphism
which sends
![]() $(x, y)$
to
$(x, y)$
to
![]() $(x+y, 0)$
. For
$(x+y, 0)$
. For
![]() $h=0$
, it corresponds to the group homomorphism
$h=0$
, it corresponds to the group homomorphism
which sends
![]() $a\otimes b$
to
$a\otimes b$
to
![]() $(a\otimes b+b\otimes a, 0)$
.
$(a\otimes b+b\otimes a, 0)$
.
Proof. Let us first suppose
![]() $h>0$
. We need to show that the unique map in the bottom row of the commutative square
$h>0$
. We need to show that the unique map in the bottom row of the commutative square
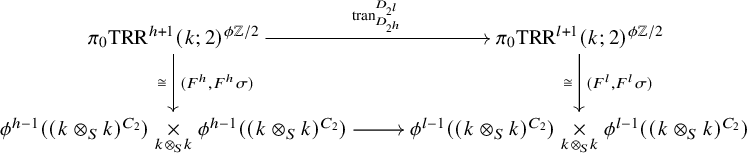
agrees with
![]() $V^{l-h}$
, where the vertical maps are the isomorphisms of Theorem 2.7 and Remark 2.8. By the double coset formula of the
$V^{l-h}$
, where the vertical maps are the isomorphisms of Theorem 2.7 and Remark 2.8. By the double coset formula of the
![]() $D_{2^l}$
-Mackey functor
$D_{2^l}$
-Mackey functor
![]() $\underline {\pi }_0{\mathrm {THR}}(k)$
, the upper composite has first component
$\underline {\pi }_0{\mathrm {THR}}(k)$
, the upper composite has first component
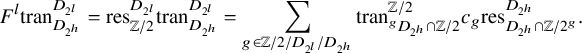 $$ \begin{align*} F^l{\mathrm{tran}}^{D_{2^l}}_{D_{2^{h}}}&={\mathrm{res}}^{D_{2^l}}_{\mathbb{Z}/2}{\mathrm{tran}}^{D_{2^l}}_{D_{2^{h}}}=\sum_{g\in \mathbb{Z}/2/D_{2^l}/D_{2^h}}{\mathrm{tran}}^{\mathbb{Z}/2}_{^gD_{2^{h}}\cap \mathbb{Z}/2} c_g{\mathrm{res}}^{D_{2^{h}}}_{D_{2^{h}}\cap \mathbb{Z}/2^g}. \end{align*} $$
$$ \begin{align*} F^l{\mathrm{tran}}^{D_{2^l}}_{D_{2^{h}}}&={\mathrm{res}}^{D_{2^l}}_{\mathbb{Z}/2}{\mathrm{tran}}^{D_{2^l}}_{D_{2^{h}}}=\sum_{g\in \mathbb{Z}/2/D_{2^l}/D_{2^h}}{\mathrm{tran}}^{\mathbb{Z}/2}_{^gD_{2^{h}}\cap \mathbb{Z}/2} c_g{\mathrm{res}}^{D_{2^{h}}}_{D_{2^{h}}\cap \mathbb{Z}/2^g}. \end{align*} $$
The double coset
![]() $\mathbb {Z}/2/D_{2^l}/D_{2^h}$
is the quotient of the cyclic group
$\mathbb {Z}/2/D_{2^l}/D_{2^h}$
is the quotient of the cyclic group
![]() $C_{2^{l-h}}$
by the involution which acts by inversion. It therefore consists of two fixed points (the unit and the rotation
$C_{2^{l-h}}$
by the involution which acts by inversion. It therefore consists of two fixed points (the unit and the rotation
![]() $g_0$
of order
$g_0$
of order
![]() $2$
in
$2$
in
![]() $D_l$
) which conjugate
$D_l$
) which conjugate
![]() $\mathbb {Z}/2$
to itself, and
$\mathbb {Z}/2$
to itself, and
![]() $(2^{l-h}-2)/2$
points whose corresponding intersection
$(2^{l-h}-2)/2$
points whose corresponding intersection
![]() $D_{2^{h}}\cap \mathbb {Z}/2^g$
is trivial. Thus,
$D_{2^{h}}\cap \mathbb {Z}/2^g$
is trivial. Thus,
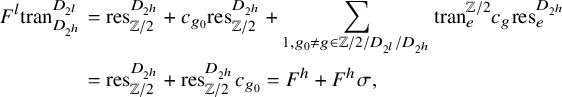 $$ \begin{align*} F^l{\mathrm{tran}}^{D_{2^l}}_{D_{2^{h}}}&={\mathrm{res}}^{D_{2^{h}}}_{\mathbb{Z}/2}+c_{g_0} {\mathrm{res}}^{D_{2^{h}}}_{\mathbb{Z}/2}+\sum_{1, g_0\neq g\in \mathbb{Z}/2/D_{2^l}/D_{2^h}}{\mathrm{tran}}^{\mathbb{Z}/2}_{e} c_g{\mathrm{res}}^{D_{2^{h}}}_{e} \\&={\mathrm{res}}^{D_{2^{h}}}_{\mathbb{Z}/2}+{\mathrm{res}}^{D_{2^{h}}}_{\mathbb{Z}/2}c_{g_0} =F^h+ F^h\sigma, \end{align*} $$
$$ \begin{align*} F^l{\mathrm{tran}}^{D_{2^l}}_{D_{2^{h}}}&={\mathrm{res}}^{D_{2^{h}}}_{\mathbb{Z}/2}+c_{g_0} {\mathrm{res}}^{D_{2^{h}}}_{\mathbb{Z}/2}+\sum_{1, g_0\neq g\in \mathbb{Z}/2/D_{2^l}/D_{2^h}}{\mathrm{tran}}^{\mathbb{Z}/2}_{e} c_g{\mathrm{res}}^{D_{2^{h}}}_{e} \\&={\mathrm{res}}^{D_{2^{h}}}_{\mathbb{Z}/2}+{\mathrm{res}}^{D_{2^{h}}}_{\mathbb{Z}/2}c_{g_0} =F^h+ F^h\sigma, \end{align*} $$
where the transfer
![]() ${\mathrm {tran}}^{\mathbb {Z}/2}_{e}$
is zero since k has characteristic
${\mathrm {tran}}^{\mathbb {Z}/2}_{e}$
is zero since k has characteristic
![]() $2$
(see [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 5.1]),
$2$
(see [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 5.1]),
![]() $\sigma $
is the action of the Weyl group of
$\sigma $
is the action of the Weyl group of
![]() $D_h$
in
$D_h$
in
![]() $D_l$
, and the equality is regarded as elements of
$D_l$
, and the equality is regarded as elements of
![]() $k\otimes _S k$
. The map
$k\otimes _S k$
. The map
![]() $F^h$
is determined in Theorem 2.7: it sends an element in the upper left corner of the square, corresponding to
$F^h$
is determined in Theorem 2.7: it sends an element in the upper left corner of the square, corresponding to
![]() $(x, y)$
in the bottom left corner, to x. Thus, the unique bottom horizontal map in the square above sends
$(x, y)$
in the bottom left corner, to x. Thus, the unique bottom horizontal map in the square above sends
![]() $(x, y)$
to the pair with first component
$(x, y)$
to the pair with first component
![]() $x+y$
.
$x+y$
.
Now let
![]() $\mathbb {Z}/2^{\prime }$
be the subgroup of
$\mathbb {Z}/2^{\prime }$
be the subgroup of
![]() $D_{l}$
generated by a reflection non-conjugate to
$D_{l}$
generated by a reflection non-conjugate to
![]() $\mathbb {Z}/2$
. Similarly to the calculation above, the second component of the top composite is
$\mathbb {Z}/2$
. Similarly to the calculation above, the second component of the top composite is
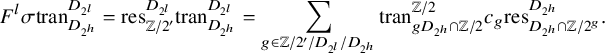 $$ \begin{align*} F^l\sigma{\mathrm{tran}}^{D_{2^l}}_{D_{2^{h}}}&={\mathrm{res}}^{D_{2^l}}_{\mathbb{Z}/2^{\prime}}{\mathrm{tran}}^{D_{2^l}}_{D_{2^{h}}}=\sum_{g\in \mathbb{Z}/2^{\prime}/D_{2^l}/D_{2^h}}{\mathrm{tran}}^{\mathbb{Z}/2}_{gD_{2^{h}}\cap \mathbb{Z}/2} c_g{\mathrm{res}}^{D_{2^{h}}}_{D_{2^{h}}\cap \mathbb{Z}/2^g}. \end{align*} $$
$$ \begin{align*} F^l\sigma{\mathrm{tran}}^{D_{2^l}}_{D_{2^{h}}}&={\mathrm{res}}^{D_{2^l}}_{\mathbb{Z}/2^{\prime}}{\mathrm{tran}}^{D_{2^l}}_{D_{2^{h}}}=\sum_{g\in \mathbb{Z}/2^{\prime}/D_{2^l}/D_{2^h}}{\mathrm{tran}}^{\mathbb{Z}/2}_{gD_{2^{h}}\cap \mathbb{Z}/2} c_g{\mathrm{res}}^{D_{2^{h}}}_{D_{2^{h}}\cap \mathbb{Z}/2^g}. \end{align*} $$
Now the double coset
![]() $\mathbb {Z}/2^{\prime }/D_{2^l}/D_{2^h}$
is the quotient of the cyclic group
$\mathbb {Z}/2^{\prime }/D_{2^l}/D_{2^h}$
is the quotient of the cyclic group
![]() $C_{2^{l-h}}$
by the free involution, and none of the conjugates of
$C_{2^{l-h}}$
by the free involution, and none of the conjugates of
![]() $\mathbb {Z}/2$
is contained in
$\mathbb {Z}/2$
is contained in
![]() $D_{2^h}$
. Thus,
$D_{2^h}$
. Thus,
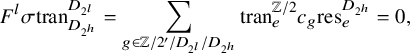 $$ \begin{align*} F^l\sigma{\mathrm{tran}}^{D_{2^l}}_{D_{2^{h}}}&=\sum_{g\in \mathbb{Z}/2^{\prime}/D_{2^l}/D_{2^h}}{\mathrm{tran}}^{\mathbb{Z}/2}_{e} c_g{\mathrm{res}}^{D_{2^{h}}}_{e}=0, \end{align*} $$
$$ \begin{align*} F^l\sigma{\mathrm{tran}}^{D_{2^l}}_{D_{2^{h}}}&=\sum_{g\in \mathbb{Z}/2^{\prime}/D_{2^l}/D_{2^h}}{\mathrm{tran}}^{\mathbb{Z}/2}_{e} c_g{\mathrm{res}}^{D_{2^{h}}}_{e}=0, \end{align*} $$
again since
![]() ${\mathrm {tran}}^{\mathbb {Z}/2}_{e}=0$
. Thus, the second component of the bottom horizontal map is null as claimed.
${\mathrm {tran}}^{\mathbb {Z}/2}_{e}=0$
. Thus, the second component of the bottom horizontal map is null as claimed.
The proof of the case
![]() $h=0$
is similar, by calculating the upper composite of the diagram
$h=0$
is similar, by calculating the upper composite of the diagram
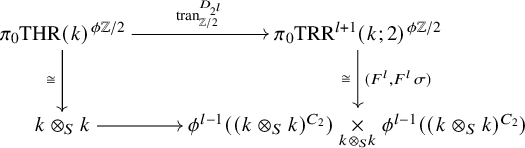
where the left vertical map is the isomorphism of [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 5.1].
Remark 2.11. The notation used in Proposition 2.10 for the transfer map is consistent with our notation for the generators of Proposition 2.9, since
The generators
![]() $\tau _n(a\otimes b)$
also have a somewhat topological interpretation, as we now explain. As seen at the end of §1, the there is a non-additive norm map
$\tau _n(a\otimes b)$
also have a somewhat topological interpretation, as we now explain. As seen at the end of §1, the there is a non-additive norm map
Moreover, since k is of characteristic
![]() $2$
, the canonical map
$2$
, the canonical map
![]() $\pi _0{\mathrm {THR}}(k)^{\mathbb {Z}/2}\to \pi _0{\mathrm {THR}}(k)^{\phi \mathbb {Z}/2}$
is an isomorphism (since the transfer from the trivial subgroup to
$\pi _0{\mathrm {THR}}(k)^{\mathbb {Z}/2}\to \pi _0{\mathrm {THR}}(k)^{\phi \mathbb {Z}/2}$
is an isomorphism (since the transfer from the trivial subgroup to
![]() $\mathbb {Z}/2$
is zero by [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 5.1]), and therefore, by post-composing with the canonical projection, we also obtain a non-additive map
$\mathbb {Z}/2$
is zero by [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 5.1]), and therefore, by post-composing with the canonical projection, we also obtain a non-additive map
on geometric fixed points, which we still denote by
![]() $N_{\mathbb {Z}/2}^{D_{2^n}}$
.
$N_{\mathbb {Z}/2}^{D_{2^n}}$
.
Proposition 2.12. Under the isomorphism of Theorem 2.7, the map
![]() $N_{\mathbb {Z}/2}^{D_{2^n}}$
corresponds to the map
$N_{\mathbb {Z}/2}^{D_{2^n}}$
corresponds to the map
![]() $N^n\colon k\otimes _S k \to \phi ^{n-1}((k\otimes _S k)^{C_2})\times _{k\otimes _S k}\phi ^{n-1}((k\otimes _S k)^{C_2})$
that sends an elementary tensor
$N^n\colon k\otimes _S k \to \phi ^{n-1}((k\otimes _S k)^{C_2})\times _{k\otimes _S k}\phi ^{n-1}((k\otimes _S k)^{C_2})$
that sends an elementary tensor
![]() $a\otimes b$
to
$a\otimes b$
to
In particular, we find that
Proof. The identification of
![]() $N^n(a\otimes b)$
is similar to the proof of Proposition 2.10. It is sufficient to show that the unique map in the bottom row of the commutative square
$N^n(a\otimes b)$
is similar to the proof of Proposition 2.10. It is sufficient to show that the unique map in the bottom row of the commutative square
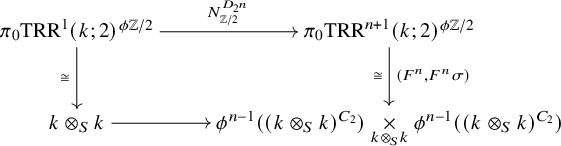
agrees with
![]() $N^n$
on the elementary tensors
$N^n$
on the elementary tensors
![]() $a\otimes b$
. Indeed, the value on a general element in the tensor product is determined by iterations of the relation
$a\otimes b$
. Indeed, the value on a general element in the tensor product is determined by iterations of the relation
By the multiplicative double coset formula of the
![]() $D_{2^l}$
-Tambara functor
$D_{2^l}$
-Tambara functor
![]() $\underline {\pi }_0{\mathrm {THR}}(k)$
, the upper composite has first component
$\underline {\pi }_0{\mathrm {THR}}(k)$
, the upper composite has first component
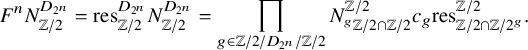 $$ \begin{align*} F^nN^{D_{2^n}}_{\mathbb{Z}/2}&={\mathrm{res}}^{D_{2^n}}_{\mathbb{Z}/2}N^{D_{2^n}}_{\mathbb{Z}/2}=\prod_{g\in \mathbb{Z}/2/D_{2^n}/\mathbb{Z}/2}N^{\mathbb{Z}/2}_{^g\mathbb{Z}/2\cap \mathbb{Z}/2} c_g{\mathrm{res}}^{\mathbb{Z}/2}_{\mathbb{Z}/2\cap \mathbb{Z}/2^g}. \end{align*} $$
$$ \begin{align*} F^nN^{D_{2^n}}_{\mathbb{Z}/2}&={\mathrm{res}}^{D_{2^n}}_{\mathbb{Z}/2}N^{D_{2^n}}_{\mathbb{Z}/2}=\prod_{g\in \mathbb{Z}/2/D_{2^n}/\mathbb{Z}/2}N^{\mathbb{Z}/2}_{^g\mathbb{Z}/2\cap \mathbb{Z}/2} c_g{\mathrm{res}}^{\mathbb{Z}/2}_{\mathbb{Z}/2\cap \mathbb{Z}/2^g}. \end{align*} $$
The double coset
![]() $\mathbb {Z}/2/D_{2^n}/\mathbb {Z}/2$
is the quotient of the cyclic group
$\mathbb {Z}/2/D_{2^n}/\mathbb {Z}/2$
is the quotient of the cyclic group
![]() $C_{2^{n}}$
by the involution which acts by inversion, and consists of two fixed points (the unit and the rotation
$C_{2^{n}}$
by the involution which acts by inversion, and consists of two fixed points (the unit and the rotation
![]() $g_0$
of order
$g_0$
of order
![]() $2$
in
$2$
in
![]() $D_n$
) which conjugate
$D_n$
) which conjugate
![]() $\mathbb {Z}/2$
to itself, and
$\mathbb {Z}/2$
to itself, and
![]() $(2^{n}-2)/2$
points whose corresponding intersection
$(2^{n}-2)/2$
points whose corresponding intersection
![]() $\mathbb {Z}/2\cap \mathbb {Z}/2^g$
is trivial. Moreover, since the cyclic group acts trivially on
$\mathbb {Z}/2\cap \mathbb {Z}/2^g$
is trivial. Moreover, since the cyclic group acts trivially on
![]() $\pi _0{\mathrm {THH}}(k)=k$
, the conjugation
$\pi _0{\mathrm {THH}}(k)=k$
, the conjugation
![]() $c_g$
is trivial except for
$c_g$
is trivial except for
![]() $g=g_0$
. Thus,
$g=g_0$
. Thus,
Since the restriction map
![]() ${\mathrm {res}}^{\mathbb {Z}/2}_e$
corresponds to the multiplication map
${\mathrm {res}}^{\mathbb {Z}/2}_e$
corresponds to the multiplication map
![]() $\mu \colon k\otimes _S k\to k$
and
$\mu \colon k\otimes _S k\to k$
and
![]() $N^{\mathbb {Z}/2}_{e}$
to the map
$N^{\mathbb {Z}/2}_{e}$
to the map
![]() $k\to k\otimes _Sk$
which sends a to
$k\to k\otimes _Sk$
which sends a to
![]() $a^2\otimes 1$
(see [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Corollary 5.2]), this sends
$a^2\otimes 1$
(see [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Corollary 5.2]), this sends
![]() $a\otimes b$
to
$a\otimes b$
to
Similarly, by letting
![]() $\mathbb {Z}/2^{\prime }$
be the subgroup of
$\mathbb {Z}/2^{\prime }$
be the subgroup of
![]() $D_{n}$
generated by a reflection non-conjugate to
$D_{n}$
generated by a reflection non-conjugate to
![]() $\mathbb {Z}/2$
, the second component of the upper composite in the square above is
$\mathbb {Z}/2$
, the second component of the upper composite in the square above is
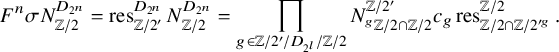
Now the double coset
![]() $\mathbb {Z}/2^{\prime }/D_{2^n}/\mathbb {Z}/2$
is the quotient of the cyclic group
$\mathbb {Z}/2^{\prime }/D_{2^n}/\mathbb {Z}/2$
is the quotient of the cyclic group
![]() $C_{2^{n}}$
by the free involution, and since
$C_{2^{n}}$
by the free involution, and since
![]() $\mathbb {Z}/2$
and
$\mathbb {Z}/2$
and
![]() $\mathbb {Z}/2^{\prime }$
are not conjugate,
$\mathbb {Z}/2^{\prime }$
are not conjugate,
Thus, the second component of the bottom horizontal map of the square sends
![]() $a\otimes b$
to
$a\otimes b$
to
This identifies the map
![]() $N^n$
as claimed. Finally, observe that
$N^n$
as claimed. Finally, observe that
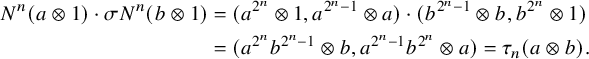 $$ \begin{align*} N^n(a\otimes 1)\cdot \sigma N^n(b\otimes 1)&=(a^{2^{n}}\otimes 1, a^{2^{n}-1}\otimes a)\cdot (b^{2^{n}-1}\otimes b, b^{2^{n}}\otimes 1) \\&=(a^{2^{n}}b^{2^{n}-1}\otimes b, a^{2^{n}-1}b^{2^{n}}\otimes a)=\tau_n(a\otimes b).\\[-42pt] \end{align*} $$
$$ \begin{align*} N^n(a\otimes 1)\cdot \sigma N^n(b\otimes 1)&=(a^{2^{n}}\otimes 1, a^{2^{n}-1}\otimes a)\cdot (b^{2^{n}-1}\otimes b, b^{2^{n}}\otimes 1) \\&=(a^{2^{n}}b^{2^{n}-1}\otimes b, a^{2^{n}-1}b^{2^{n}}\otimes a)=\tau_n(a\otimes b).\\[-42pt] \end{align*} $$
Remark 2.13. For the usual Witt vectors, the elements
![]() $\tau _n(a)=(a, 0, \dots , 0)$
assemble into a (non-additive) multiplicative map
$\tau _n(a)=(a, 0, \dots , 0)$
assemble into a (non-additive) multiplicative map
![]() $\tau _n\colon R\to W_{\langle 2^n\rangle }(R)$
, which is a section for the truncation map R. We do not think that this is the case for
$\tau _n\colon R\to W_{\langle 2^n\rangle }(R)$
, which is a section for the truncation map R. We do not think that this is the case for
![]() $\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
since there seems to be no way of extending
$\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
since there seems to be no way of extending
![]() $\tau _n(a\otimes b)$
to a sum of elementary tensors. Even without a canonical splitting for the truncation map
$\tau _n(a\otimes b)$
to a sum of elementary tensors. Even without a canonical splitting for the truncation map
![]() $R\colon \pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}\to \pi _0\ {\mathrm {TRR}}^{1}(k;2)^{\phi \mathbb {Z}/2}$
at hand, having a set of generators for
$R\colon \pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}\to \pi _0\ {\mathrm {TRR}}^{1}(k;2)^{\phi \mathbb {Z}/2}$
at hand, having a set of generators for
![]() $\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
defined from the
$\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
defined from the
![]() $\tau _i(a\otimes b)$
will suffice for our purposes.
$\tau _i(a\otimes b)$
will suffice for our purposes.
2.3 The fundamental ideal of TRR
The components of the geometric fixed points of any connective
![]() $\mathbb {Z}/2$
-spectrum X admit a restriction map, defined as the canonical map of cokernels
$\mathbb {Z}/2$
-spectrum X admit a restriction map, defined as the canonical map of cokernels
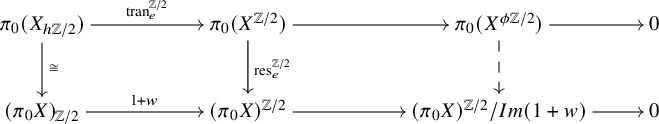
where w is the action of the generator of
![]() $\mathbb {Z}/2$
on
$\mathbb {Z}/2$
on
![]() $\pi _0X$
. This map is moreover a monoidal natural transformation. By applying this construction to the
$\pi _0X$
. This map is moreover a monoidal natural transformation. By applying this construction to the
![]() $\mathbb {Z}/2$
-spectrum
$\mathbb {Z}/2$
-spectrum
![]() ${\mathrm {TRR}}^{n+1}(k;2)$
, we obtain a ring homomorphism which we denote by
${\mathrm {TRR}}^{n+1}(k;2)$
, we obtain a ring homomorphism which we denote by
Here,
![]() ${\mathrm {W}}_{\langle 2^{n}\rangle }(k)$
is the ring of
${\mathrm {W}}_{\langle 2^{n}\rangle }(k)$
is the ring of
![]() $(n+1)$
-truncated
$(n+1)$
-truncated
![]() $2$
-typical Witt vectors of k, and the isomorphism is from [Reference Hesselholt and MadsenHM97, Theorem F]. Here, we use that the isomorphism of [Reference Hesselholt and MadsenHM97, Theorem F] is
$2$
-typical Witt vectors of k, and the isomorphism is from [Reference Hesselholt and MadsenHM97, Theorem F]. Here, we use that the isomorphism of [Reference Hesselholt and MadsenHM97, Theorem F] is
![]() $\mathbb {Z}/2$
-equivariant, where the
$\mathbb {Z}/2$
-equivariant, where the
![]() $\mathbb {Z}/2$
-action on
$\mathbb {Z}/2$
-action on
![]() ${\mathrm {W}}_{\langle 2^{n}\rangle }(k)$
is trivial (see the proof of [Reference Dotto, Patchkoria and Jonsson MoiDPM22, Theorem 3.7], where the first paragraph of page 522 holds also for
${\mathrm {W}}_{\langle 2^{n}\rangle }(k)$
is trivial (see the proof of [Reference Dotto, Patchkoria and Jonsson MoiDPM22, Theorem 3.7], where the first paragraph of page 522 holds also for
![]() $p=2$
. This can more generally be applied to the case where k has a nontrivial involution, in which case the involution on
$p=2$
. This can more generally be applied to the case where k has a nontrivial involution, in which case the involution on
![]() $\pi _0{\mathrm {TR}}^{n+1}(k;2)$
corresponds to the map induced on
$\pi _0{\mathrm {TR}}^{n+1}(k;2)$
corresponds to the map induced on
![]() ${\mathrm {W}}_{\langle 2^{n}\rangle }(k)$
by the involution on k under the functoriality of the Witt vectors).
${\mathrm {W}}_{\langle 2^{n}\rangle }(k)$
by the involution on k under the functoriality of the Witt vectors).
The goal of this section is to describe explicitly the map
![]() ${\mathrm {res}}^{D_{2^n}}_{C_{2^n}}$
under the isomorphism of Theorem 2.7, and provide generators for its kernel. We recall that for every commutative ring R, as a set,
${\mathrm {res}}^{D_{2^n}}_{C_{2^n}}$
under the isomorphism of Theorem 2.7, and provide generators for its kernel. We recall that for every commutative ring R, as a set,
![]() ${\mathrm {W}}_{\langle 2^{n}\rangle }(R)=R^{\times n+1}$
, with the unique functorial ring structure which makes the Witt polynomials into ring homomorphisms. For any
${\mathrm {W}}_{\langle 2^{n}\rangle }(R)=R^{\times n+1}$
, with the unique functorial ring structure which makes the Witt polynomials into ring homomorphisms. For any
![]() ${\mathbb {F}}_2$
-algebra R, we moreover have that as a set
${\mathbb {F}}_2$
-algebra R, we moreover have that as a set
We denote by
![]() $V^{n-i}\tau _i(a)=(0, \dots , 0, a, 0, \dots , 0)$
the canonical additive generators of
$V^{n-i}\tau _i(a)=(0, \dots , 0, a, 0, \dots , 0)$
the canonical additive generators of
![]() ${\mathrm {W}}_{\langle 2^{n}\rangle }(R)$
, for
${\mathrm {W}}_{\langle 2^{n}\rangle }(R)$
, for
![]() $a\in R$
.
$a\in R$
.
Proposition 2.14. Let k be a field of characteristic
![]() $2$
, and
$2$
, and
![]() $n\geq 1$
. Under the isomorphisms of Theorem 2.7 and [Reference Hesselholt and MadsenHM97, Theorem F], the restriction map corresponds to the unique ring homomorphism
$n\geq 1$
. Under the isomorphisms of Theorem 2.7 and [Reference Hesselholt and MadsenHM97, Theorem F], the restriction map corresponds to the unique ring homomorphism
which sends the respective generators of Proposition 2.9 to
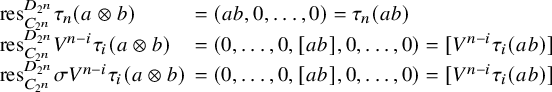 $$\begin{align*}\begin{array}{ll} {\mathrm{res}}^{D_{2^n}}_{C_{2^n}}\tau_n(a\otimes b)&=(ab, 0, \dots, 0)=\tau_n(ab) \\ {\mathrm{res}}^{D_{2^n}}_{C_{2^n}}V^{n-i}\tau_i(a\otimes b)&=(0, \dots, 0, [ab], 0, \dots, 0)=[V^{n-i}\tau_{i}(ab)] \\ {\mathrm{res}}^{D_{2^n}}_{C_{2^n}}\sigma V^{n-i}\tau_i(a\otimes b)&=(0, \dots, 0, [ab], 0, \dots, 0)=[V^{n-i}\tau_{i}(ab)] \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{ll} {\mathrm{res}}^{D_{2^n}}_{C_{2^n}}\tau_n(a\otimes b)&=(ab, 0, \dots, 0)=\tau_n(ab) \\ {\mathrm{res}}^{D_{2^n}}_{C_{2^n}}V^{n-i}\tau_i(a\otimes b)&=(0, \dots, 0, [ab], 0, \dots, 0)=[V^{n-i}\tau_{i}(ab)] \\ {\mathrm{res}}^{D_{2^n}}_{C_{2^n}}\sigma V^{n-i}\tau_i(a\otimes b)&=(0, \dots, 0, [ab], 0, \dots, 0)=[V^{n-i}\tau_{i}(ab)] \end{array} \end{align*}$$
for all
![]() $0\leq i\leq n-1$
, where the mod
$0\leq i\leq n-1$
, where the mod
![]() $k^2$
reduction
$k^2$
reduction
![]() $[ab]$
of
$[ab]$
of
![]() $ab$
sits in the
$ab$
sits in the
![]() $(n-i+1)$
-st component.
$(n-i+1)$
-st component.
Proof. Since
![]() $\underline {\pi _0}\ {\mathrm {THR}}(k)$
is a
$\underline {\pi _0}\ {\mathrm {THR}}(k)$
is a
![]() $D_{2^n}$
-Tambara functor, the restriction
$D_{2^n}$
-Tambara functor, the restriction
![]() ${\mathrm {res}}^{D_{2^n}}_{C_{2^n}}$
is a ring homomorphism, and by the double-coset formulas, it commutes with norms and transfers, and with the Weyl action. The operators
${\mathrm {res}}^{D_{2^n}}_{C_{2^n}}$
is a ring homomorphism, and by the double-coset formulas, it commutes with norms and transfers, and with the Weyl action. The operators
![]() $V^{n-i}$
and
$V^{n-i}$
and
![]() $\tau _i$
are described in terms of norms and transfers by Propositions 2.10 and 2.12, and by [Reference Hesselholt and MadsenHM97, Theorem 3.3] for the usual Witt vectors. It therefore follows that
$\tau _i$
are described in terms of norms and transfers by Propositions 2.10 and 2.12, and by [Reference Hesselholt and MadsenHM97, Theorem 3.3] for the usual Witt vectors. It therefore follows that
where
![]() ${\mathrm {res}}^{\mathbb {Z}/2}_{e}$
is the multiplication map of
${\mathrm {res}}^{\mathbb {Z}/2}_{e}$
is the multiplication map of
![]() $k\otimes _S k$
by [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 5.1]. The proof for the other generators is similar.
$k\otimes _S k$
by [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 5.1]. The proof for the other generators is similar.
Definition 2.15. The fundamental ideal
![]() $J_{\langle 2^n\rangle }$
of
$J_{\langle 2^n\rangle }$
of
![]() $\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
is the kernel of the ring homomorphism
$\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
is the kernel of the ring homomorphism
from Proposition 2.14, for
![]() $n\geq 1$
, and for
$n\geq 1$
, and for
![]() $n=0$
, it is the kernel of the multiplication map
$n=0$
, it is the kernel of the multiplication map
Proposition 2.16. For every
![]() $n\geq 0$
,
$n\geq 0$
,
![]() $J_{\langle 2^n\rangle }$
is the subgroup of
$J_{\langle 2^n\rangle }$
is the subgroup of
![]() $\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
generated by the elements
$\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
generated by the elements
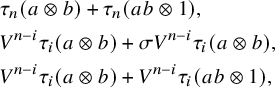 $$ \begin{align*} &\tau_n(a\otimes b)+\tau_n(ab\otimes 1), \\ &V^{n-i}\tau_i(a\otimes b)+\sigma V^{n-i}\tau_i(a\otimes b), \\ &V^{n-i}\tau_i(a\otimes b)+V^{n-i}\tau_i(ab\otimes 1), \end{align*} $$
$$ \begin{align*} &\tau_n(a\otimes b)+\tau_n(ab\otimes 1), \\ &V^{n-i}\tau_i(a\otimes b)+\sigma V^{n-i}\tau_i(a\otimes b), \\ &V^{n-i}\tau_i(a\otimes b)+V^{n-i}\tau_i(ab\otimes 1), \end{align*} $$
for all
![]() $0\leq i\leq n-1$
and
$0\leq i\leq n-1$
and
![]() $a\otimes b\in k\otimes _S k$
.
$a\otimes b\in k\otimes _S k$
.
Proof. The proof is by induction on n. For
![]() $n=0$
, this is the claim that the kernel of the multiplication map
$n=0$
, this is the claim that the kernel of the multiplication map
is generated by
![]() $a\otimes b+ab\otimes 1$
for
$a\otimes b+ab\otimes 1$
for
![]() $a\otimes b\in k\otimes _S k$
, which is clear.
$a\otimes b\in k\otimes _S k$
, which is clear.
Now suppose the claim holds for n, and consider the commutative diagram with exact rows
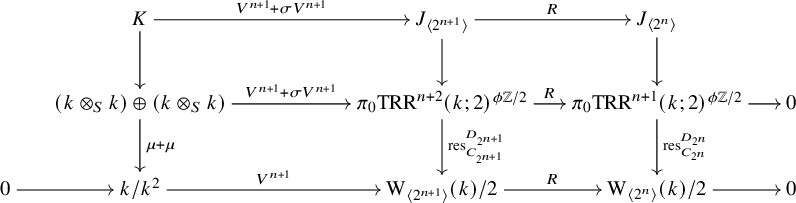
where the vertical maps from the top row to the middle row are kernel inclusions. The middle row is exact by [Reference Dotto, Moi and PatchkoriaDMP24, Proof of Theorem 4.9], or by the explicit calculation of Theorem 2.7 and Proposition 2.10. Thus, if we find a set of generators for K and show that the map R in the first row is surjective, then
![]() $J_{\langle 2^{n+1}\rangle }$
is generated by the image by
$J_{\langle 2^{n+1}\rangle }$
is generated by the image by
![]() $V^{n+1}+\sigma V^{n+1}$
of the generators of K, and by a choice of lifts of the generators of
$V^{n+1}+\sigma V^{n+1}$
of the generators of K, and by a choice of lifts of the generators of
![]() $J_{\langle 2^{n}\rangle }$
given by the inductive assumption. The kernel K consists of those elements
$J_{\langle 2^{n}\rangle }$
given by the inductive assumption. The kernel K consists of those elements
![]() $(x, y)$
such that
$(x, y)$
such that
![]() $\mu (x)+\mu (y)$
is a square in k. Since every square
$\mu (x)+\mu (y)$
is a square in k. Since every square
![]() $c^2$
in k is hit by
$c^2$
in k is hit by
![]() $c\otimes c$
under
$c\otimes c$
under
![]() $\mu $
, K is the subgroup of elements of the form
$\mu $
, K is the subgroup of elements of the form
![]() $(x, y)$
, where
$(x, y)$
, where
for some
![]() $c\in k$
and
$c\in k$
and
![]() $z\in \ker (\mu )$
. Since the kernel of
$z\in \ker (\mu )$
. Since the kernel of
![]() $\mu $
is generated by elements of the form
$\mu $
is generated by elements of the form
![]() $a\otimes b+ab\otimes 1$
, we conclude that K is generated by elements of the form
$a\otimes b+ab\otimes 1$
, we conclude that K is generated by elements of the form
![]() $(a\otimes b, a\otimes b)$
, and elements of the form
$(a\otimes b, a\otimes b)$
, and elements of the form
![]() $(a\otimes b+ab\otimes 1+c\otimes c, 0)$
. The images of these generators by
$(a\otimes b+ab\otimes 1+c\otimes c, 0)$
. The images of these generators by
![]() $V^{n+1}+\sigma V^{n+1}$
are respectively of the form
$V^{n+1}+\sigma V^{n+1}$
are respectively of the form
and
where
![]() $V^{n+1}(c\otimes c)=0$
by Proposition 2.10. It therefore remains to show that by applying R to the elements
$V^{n+1}(c\otimes c)=0$
by Proposition 2.10. It therefore remains to show that by applying R to the elements
![]() $\tau _{n+1}(a\otimes b)+\tau _{n+1}(ab\otimes 1)$
,
$\tau _{n+1}(a\otimes b)+\tau _{n+1}(ab\otimes 1)$
,
![]() $V^{n+1-i}\tau _i(a\otimes b)+\sigma V^{n+1-i}\tau _i(a\otimes b)$
and
$V^{n+1-i}\tau _i(a\otimes b)+\sigma V^{n+1-i}\tau _i(a\otimes b)$
and
![]() $V^{n+1-i}\tau _i(a\otimes b)+V^{n+1-i}\tau _i(ab\otimes 1)$
, for
$V^{n+1-i}\tau _i(a\otimes b)+V^{n+1-i}\tau _i(ab\otimes 1)$
, for
![]() $1\leq i\leq n$
, we hit all the generators of
$1\leq i\leq n$
, we hit all the generators of
![]() $J_{\langle 2^{n}\rangle }$
given by the inductive assumption. This is the case since
$J_{\langle 2^{n}\rangle }$
given by the inductive assumption. This is the case since
![]() $R\tau _{i+1}=\tau _i$
,
$R\tau _{i+1}=\tau _i$
,
![]() $RV^{n+1-i}=V^{n-i}R$
, and
$RV^{n+1-i}=V^{n-i}R$
, and
![]() $R\sigma =\sigma R$
, by Theorem 2.7 and Proposition 2.10.
$R\sigma =\sigma R$
, by Theorem 2.7 and Proposition 2.10.
Corollary 2.17. For every
![]() $n\geq 0$
, the ideal
$n\geq 0$
, the ideal
![]() $J_{\langle 2^n\rangle }$
is generated, as a
$J_{\langle 2^n\rangle }$
is generated, as a
![]() $\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
-module, by the elements of the form
$\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
-module, by the elements of the form
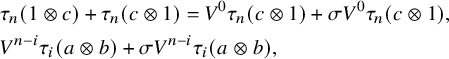 $$ \begin{align*} &\tau_n(1\otimes c)+\tau_n(c\otimes 1)=V^{0}\tau_n(c\otimes 1)+\sigma V^{0}\tau_n(c\otimes 1), \\ &V^{n-i}\tau_i(a\otimes b)+\sigma V^{n-i}\tau_i(a\otimes b), \end{align*} $$
$$ \begin{align*} &\tau_n(1\otimes c)+\tau_n(c\otimes 1)=V^{0}\tau_n(c\otimes 1)+\sigma V^{0}\tau_n(c\otimes 1), \\ &V^{n-i}\tau_i(a\otimes b)+\sigma V^{n-i}\tau_i(a\otimes b), \end{align*} $$
for all
![]() $0\leq i\leq n-1$
,
$0\leq i\leq n-1$
,
![]() $a\otimes b\in k\otimes _S k$
and
$a\otimes b\in k\otimes _S k$
and
![]() $c\in k$
. In particular,
$c\in k$
. In particular,
![]() $J_{\langle 2^n\rangle }$
is generated, as a
$J_{\langle 2^n\rangle }$
is generated, as a
![]() $\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
-module, by fixed points for the involution
$\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
-module, by fixed points for the involution
![]() $\sigma $
.
$\sigma $
.
Proof. By Proposition 2.16, the corollary follows from the identities
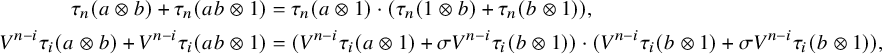 $$ \begin{align*} \tau_n(a\otimes b)+\tau_n(ab\otimes 1)&=\tau_{n}(a\otimes 1)\cdot(\tau_n(1\otimes b)+\tau_n(b\otimes 1)), \\ V^{n-i}\tau_i(a\otimes b)+V^{n-i}\tau_i(ab\otimes 1)&=(V^{n-i}\tau_i(a\otimes 1)+\sigma V^{n-i}\tau_i(b\otimes 1))\cdot (V^{n-i}\tau_i(b\otimes 1)+\sigma V^{n-i}\tau_i(b\otimes 1)), \end{align*} $$
$$ \begin{align*} \tau_n(a\otimes b)+\tau_n(ab\otimes 1)&=\tau_{n}(a\otimes 1)\cdot(\tau_n(1\otimes b)+\tau_n(b\otimes 1)), \\ V^{n-i}\tau_i(a\otimes b)+V^{n-i}\tau_i(ab\otimes 1)&=(V^{n-i}\tau_i(a\otimes 1)+\sigma V^{n-i}\tau_i(b\otimes 1))\cdot (V^{n-i}\tau_i(b\otimes 1)+\sigma V^{n-i}\tau_i(b\otimes 1)), \end{align*} $$
which can be easily verified from the definitions.
3 Real TR and the de Rham-Witt complex
3.1 The Witt complex associated to TRR
Since the operators
![]() $F, V, \sigma $
and R of Theorem 2.7 and Proposition 2.10 commute with the restriction map to the Witt vectors modulo
$F, V, \sigma $
and R of Theorem 2.7 and Proposition 2.10 commute with the restriction map to the Witt vectors modulo
![]() $2$
, they induce maps on the fundamental ideals
$2$
, they induce maps on the fundamental ideals
for all
![]() $n\geq 0$
.
$n\geq 0$
.
Proposition 3.1. For every integer
![]() $q\geq 2$
, the maps
$q\geq 2$
, the maps
![]() $F, R, V, \sigma $
above restrict to maps
$F, R, V, \sigma $
above restrict to maps
Moreover,
![]() $1+\sigma $
induces a well-defined map
$1+\sigma $
induces a well-defined map
which satisfies
![]() $(1+\sigma )^2=0$
.
$(1+\sigma )^2=0$
.
Proof. The claim about
![]() $R, F$
and
$R, F$
and
![]() $\sigma $
are clear since these maps are multiplicative. For the map V, we employ Corollary 2.17. First suppose that
$\sigma $
are clear since these maps are multiplicative. For the map V, we employ Corollary 2.17. First suppose that
![]() $n\geq 1$
, so that the power
$n\geq 1$
, so that the power
![]() $J_{\langle 2^{n}\rangle }^q$
is additively generated by elements of the form
$J_{\langle 2^{n}\rangle }^q$
is additively generated by elements of the form
where
![]() $(x, y)$
is a generator of
$(x, y)$
is a generator of
![]() $\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
from Proposition 2.9, and
$\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
from Proposition 2.9, and
![]() $(x_l, x_l)$
is a generator of
$(x_l, x_l)$
is a generator of
![]() $J_{\langle 2^{n}\rangle }$
from Corollary 2.17, which is diagonal since they are invariant by the Weyl action
$J_{\langle 2^{n}\rangle }$
from Corollary 2.17, which is diagonal since they are invariant by the Weyl action
![]() $\sigma $
. Since V is additive, it is sufficient to show that V sends these elements to
$\sigma $
. Since V is additive, it is sufficient to show that V sends these elements to
![]() $J_{\langle 2^{n+1}\rangle }^q $
. Now by Proposition 2.10, we have that
$J_{\langle 2^{n+1}\rangle }^q $
. Now by Proposition 2.10, we have that
 $$ \begin{align*} V(xx_1\dots x_q, yx_1\dots x_q)&=((x+y)x_1\dots x_q, 0) \\&=(x+y, x+y)\cdot (x_1, x_1)\cdot\dots\cdot (x_{q-2}, x_{q-2})\cdot (x_{q-1}, x_{q-1})\cdot(x_q, 0). \end{align*} $$
$$ \begin{align*} V(xx_1\dots x_q, yx_1\dots x_q)&=((x+y)x_1\dots x_q, 0) \\&=(x+y, x+y)\cdot (x_1, x_1)\cdot\dots\cdot (x_{q-2}, x_{q-2})\cdot (x_{q-1}, x_{q-1})\cdot(x_q, 0). \end{align*} $$
The first factor is
which belongs to
![]() $J_{\langle 2^{n+1}\rangle }$
since it is sent to zero by the restriction map by Proposition 2.14. By Corollary 2.17, each of the factors
$J_{\langle 2^{n+1}\rangle }$
since it is sent to zero by the restriction map by Proposition 2.14. By Corollary 2.17, each of the factors
![]() $(x_1, x_1), \dots , (x_{q-1}, x_{q-1})$
is of the form
$(x_1, x_1), \dots , (x_{q-1}, x_{q-1})$
is of the form
for some
![]() $0\leq i\leq n$
, which as an element of
$0\leq i\leq n$
, which as an element of
![]() $\pi _0\ {\mathrm {TRR}}^{n+2}(k;2)^{\phi \mathbb {Z}/2}$
is of the form
$\pi _0\ {\mathrm {TRR}}^{n+2}(k;2)^{\phi \mathbb {Z}/2}$
is of the form
for
![]() $0\leq i\leq n$
, and therefore belongs to
$0\leq i\leq n$
, and therefore belongs to
![]() $J_{\langle 2^{n+1}\rangle }$
. Thus, it suffices to show that
$J_{\langle 2^{n+1}\rangle }$
. Thus, it suffices to show that
![]() $(x_{q-1}, x_{q-1})\cdot (x_q, 0)$
is also in
$(x_{q-1}, x_{q-1})\cdot (x_q, 0)$
is also in
![]() $J_{\langle 2^{n+1}\rangle }$
. But since
$J_{\langle 2^{n+1}\rangle }$
. But since
![]() $(x_q, x_q)$
is of the form
$(x_q, x_q)$
is of the form
![]() $V^{n-i}\tau _i(a\otimes b)+\sigma V^{n-i}\tau _i(a\otimes b)$
, we have that
$V^{n-i}\tau _i(a\otimes b)+\sigma V^{n-i}\tau _i(a\otimes b)$
, we have that
![]() $(x_q, 0)$
is a well-defined element of
$(x_q, 0)$
is a well-defined element of
![]() $\pi _0\ {\mathrm {TRR}}^{n+2}(k;2)^{\phi \mathbb {Z}/2}$
, and since
$\pi _0\ {\mathrm {TRR}}^{n+2}(k;2)^{\phi \mathbb {Z}/2}$
, and since
![]() $J_{\langle 2^{n+1}\rangle }$
is an ideal,
$J_{\langle 2^{n+1}\rangle }$
is an ideal,
![]() $ (x_{q-1}, x_{q-1})\cdot (x_q, 0)$
indeed belongs to
$ (x_{q-1}, x_{q-1})\cdot (x_q, 0)$
indeed belongs to
![]() $J_{\langle 2^{n+1}\rangle }$
.
$J_{\langle 2^{n+1}\rangle }$
.
If
![]() $n=0$
, the ideal
$n=0$
, the ideal
![]() $J_{\langle 1\rangle }^q$
of
$J_{\langle 1\rangle }^q$
of
![]() $k\otimes _Sk$
is additively generated by elements of the form
$k\otimes _Sk$
is additively generated by elements of the form
![]() $xx_1\dots x_q$
with
$xx_1\dots x_q$
with
![]() $x\in k\otimes _S k$
and
$x\in k\otimes _S k$
and
![]() $x_1, \dots , x_q$
fixed by the involution w. Then by Proposition 2.10,
$x_1, \dots , x_q$
fixed by the involution w. Then by Proposition 2.10,
and one can repeat the argument used in the case
![]() $n\geq 1$
.
$n\geq 1$
.
Finally, let us show that
![]() $1+\sigma $
sends
$1+\sigma $
sends
![]() $J_{\langle 2^{n}\rangle }^q$
to
$J_{\langle 2^{n}\rangle }^q$
to
![]() $J_{\langle 2^{n}\rangle }^{q+1}$
. By Corollary 2.17, every element of
$J_{\langle 2^{n}\rangle }^{q+1}$
. By Corollary 2.17, every element of
![]() $J_{\langle 2^{n}\rangle }^q $
is a sum of elements of the form
$J_{\langle 2^{n}\rangle }^q $
is a sum of elements of the form
![]() $z\cdot g_1\cdot \dots \cdot g_q$
with
$z\cdot g_1\cdot \dots \cdot g_q$
with
![]() $z\in \pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
and each
$z\in \pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
and each
![]() $g_i\in J_{\langle 2^{n}\rangle }$
fixed by
$g_i\in J_{\langle 2^{n}\rangle }$
fixed by
![]() $\sigma $
. Since
$\sigma $
. Since
![]() $1+\sigma $
is additive, we only need to show that these elements are sent to
$1+\sigma $
is additive, we only need to show that these elements are sent to
![]() $J_{\langle 2^{n}\rangle }^{q+1}$
. Since
$J_{\langle 2^{n}\rangle }^{q+1}$
. Since
![]() $\sigma $
is multiplicative, we have that
$\sigma $
is multiplicative, we have that
It therefore suffices to show that
![]() $z+\sigma (z)$
belongs to
$z+\sigma (z)$
belongs to
![]() $J_{\langle 2^{n}\rangle }$
, which is the case since the restriction map to the Witt vectors modulo
$J_{\langle 2^{n}\rangle }$
, which is the case since the restriction map to the Witt vectors modulo
![]() $2$
is invariant under the action of
$2$
is invariant under the action of
![]() $\sigma $
. Clearly, since
$\sigma $
. Clearly, since
![]() $\sigma ^2$
is the identity, we have that
$\sigma ^2$
is the identity, we have that
![]() $(1+\sigma )^2=0$
.
$(1+\sigma )^2=0$
.
For every
![]() $n\geq 0$
, let us denote by
$n\geq 0$
, let us denote by
![]() $J_{\langle 2^{n}\rangle }^\ast /J_{\langle 2^{n}\rangle }^{\ast +1}$
the graded ring defined by the quotients
$J_{\langle 2^{n}\rangle }^\ast /J_{\langle 2^{n}\rangle }^{\ast +1}$
the graded ring defined by the quotients
![]() $J_{\langle 2^{n}\rangle }^q/J_{\langle 2^{n}\rangle }^{q+1}$
for
$J_{\langle 2^{n}\rangle }^q/J_{\langle 2^{n}\rangle }^{q+1}$
for
![]() $q\geq 0$
, and by the multiplication of
$q\geq 0$
, and by the multiplication of
![]() $J_{\langle 2^{n}\rangle }$
. We will show that the sequence of graded rings
$J_{\langle 2^{n}\rangle }$
. We will show that the sequence of graded rings
![]() $J_{\langle 2^{n}\rangle }^\ast /J_{\langle 2^{n}\rangle }^{\ast +1}$
where
$J_{\langle 2^{n}\rangle }^\ast /J_{\langle 2^{n}\rangle }^{\ast +1}$
where
![]() $n\geq 0$
, equipped with the operators
$n\geq 0$
, equipped with the operators
![]() $R, F, V$
and
$R, F, V$
and
![]() $d:=(1+\sigma )$
, define the structure of a
$d:=(1+\sigma )$
, define the structure of a
![]() $2$
-typical Witt complex. We recall its definition, from [Reference CosteanuCos08], in the special case where the base ring has characteristic
$2$
-typical Witt complex. We recall its definition, from [Reference CosteanuCos08], in the special case where the base ring has characteristic
![]() $2$
. In this case, item v) simplifies since
$2$
. In this case, item v) simplifies since
![]() $d\log [-1]=0$
, and the definition agrees to the one for odd primes from [Reference Hesselholt and MadsenHM04].
$d\log [-1]=0$
, and the definition agrees to the one for odd primes from [Reference Hesselholt and MadsenHM04].
Definition 3.2 [Reference CosteanuCos08]
A
![]() $2$
-typical Witt complex over an
$2$
-typical Witt complex over an
![]() ${\mathbb {F}}_2$
-algebra A consists of
${\mathbb {F}}_2$
-algebra A consists of
-
i) a graded-commutative pro-graded ring
 $\{E^{\ast }_n, R\colon E^{\ast }_{n+1}\to E^{\ast }_n\}_{n\geq 0}$
,
$\{E^{\ast }_n, R\colon E^{\ast }_{n+1}\to E^{\ast }_n\}_{n\geq 0}$
, -
ii) a strict map of pro-rings
 $\lambda \colon {\mathrm {W}}_{\langle 2^{\bullet }\rangle }(A)\to E^{0}_\bullet $
from the pro-ring of
$\lambda \colon {\mathrm {W}}_{\langle 2^{\bullet }\rangle }(A)\to E^{0}_\bullet $
from the pro-ring of
 $2$
-typical Witt vectors of A,
$2$
-typical Witt vectors of A, -
iii) a strict map of pro-graded rings
 $F\colon E^{\ast }_{\bullet +1}\longrightarrow E^{\ast }_\bullet $
such that
$F\colon E^{\ast }_{\bullet +1}\longrightarrow E^{\ast }_\bullet $
such that
 $\lambda F=F\lambda $
,
$\lambda F=F\lambda $
, -
iv) a strict map of pro-graded
 $E^{\ast }_\bullet $
-modules
$E^{\ast }_\bullet $
-modules
 $V\colon F^{\ast }E^{\ast }_\bullet \longrightarrow E^{\ast }_{\bullet +1}$
such that
$V\colon F^{\ast }E^{\ast }_\bullet \longrightarrow E^{\ast }_{\bullet +1}$
such that
 $\lambda V=V\lambda $
and
$\lambda V=V\lambda $
and
 $FV=2$
. The linearity of V means that
$FV=2$
. The linearity of V means that
 $V (x)y = V (xF (y))$
for all
$V (x)y = V (xF (y))$
for all
 $x\in E^{\ast }_n$
and
$x\in E^{\ast }_n$
and
 $y\in E^{\ast }_{n+1}$
,
$y\in E^{\ast }_{n+1}$
, -
v) a strict map of pro-graded abelian groups
 $d\colon E^{\ast }_\bullet \to E^{\ast +1}_\bullet $
, which is a derivation, in the sense that for all
$d\colon E^{\ast }_\bullet \to E^{\ast +1}_\bullet $
, which is a derivation, in the sense that for all $$\begin{align*}d(xy)=d(x)y+(-1)^{|x|}xd(y)\end{align*}$$
$$\begin{align*}d(xy)=d(x)y+(-1)^{|x|}xd(y)\end{align*}$$
 $x, y\in E^{\ast }_n$
, and which satisfies the relations where
$x, y\in E^{\ast }_n$
, and which satisfies the relations where $$ \begin{align*} FdV&=d \\ dd&=0 \\ Fd\lambda\tau_n&=(\lambda\tau_{n-1})\cdot (d\lambda\tau_{n-1}), \end{align*} $$
$$ \begin{align*} FdV&=d \\ dd&=0 \\ Fd\lambda\tau_n&=(\lambda\tau_{n-1})\cdot (d\lambda\tau_{n-1}), \end{align*} $$
 $\tau _n\colon A\to {\mathrm {W}}_{\langle 2^{n}\rangle }(A)$
is the Teichmüller map sending a to
$\tau _n\colon A\to {\mathrm {W}}_{\langle 2^{n}\rangle }(A)$
is the Teichmüller map sending a to
 $(a, 0, \dots , 0)$
.
$(a, 0, \dots , 0)$
.
Before showing that the graded ring defined by the ideals
![]() $J_{\langle 2^{n}\rangle }$
admits the structure of a Witt-complex, let us point out that since the map
$J_{\langle 2^{n}\rangle }$
admits the structure of a Witt-complex, let us point out that since the map
![]() ${\mathrm {res}}^{D_{2^n}}_{C_{2^n}}$
is surjective by Propositions 2.14, it induces an isomorphism
${\mathrm {res}}^{D_{2^n}}_{C_{2^n}}$
is surjective by Propositions 2.14, it induces an isomorphism
where the last isomorphism is from [Reference Hesselholt and MadsenHM97, Theorem F].
Proposition 3.3. The sequence of graded rings
![]() $\{J_{\langle 2^{n}\rangle }^\ast /J_{\langle 2^{n}\rangle }^{\ast +1}\}_{n\geq 0}$
equipped with the operators
$\{J_{\langle 2^{n}\rangle }^\ast /J_{\langle 2^{n}\rangle }^{\ast +1}\}_{n\geq 0}$
equipped with the operators
![]() $R, F, V$
and
$R, F, V$
and
![]() $ d:=(1+\sigma )$
from Proposition 3.1, and the quotient maps
$ d:=(1+\sigma )$
from Proposition 3.1, and the quotient maps
defines a
![]() $2$
-typical Witt complex over the field k of characteristic
$2$
-typical Witt complex over the field k of characteristic
![]() $2$
.
$2$
.
Proof. First of all, the maps
![]() $R, F, V$
and
$R, F, V$
and
![]() $ d:=(1+\sigma )$
are well defined on the quotients of the powers of the ideals by Proposition 3.1. Axioms i)–iv) of Definition 3.2 follow immediately from either the fact that
$ d:=(1+\sigma )$
are well defined on the quotients of the powers of the ideals by Proposition 3.1. Axioms i)–iv) of Definition 3.2 follow immediately from either the fact that
![]() $F, V$
and
$F, V$
and
![]() ${\mathrm {res}}^{D_{2^n}}_{C_{2^n}}$
are induced from the maps of a Mackey functor, or from their explicit formulas from Theorem 2.7 and Propositions 2.10 and 2.14. This is except from the identity
${\mathrm {res}}^{D_{2^n}}_{C_{2^n}}$
are induced from the maps of a Mackey functor, or from their explicit formulas from Theorem 2.7 and Propositions 2.10 and 2.14. This is except from the identity
![]() $FV=2$
(which in our case is zero), since by these arguments, we only know that
$FV=2$
(which in our case is zero), since by these arguments, we only know that
![]() $FV=1+\sigma $
. However, for every
$FV=1+\sigma $
. However, for every
![]() $x\in J_{\langle 2^{n}\rangle }^q$
, we have that
$x\in J_{\langle 2^{n}\rangle }^q$
, we have that
belongs to
![]() $J_{\langle 2^{n}\rangle }^{q+1}$
by Proposition 3.1, and it is therefore indeed zero in
$J_{\langle 2^{n}\rangle }^{q+1}$
by Proposition 3.1, and it is therefore indeed zero in
![]() $J_{\langle 2^{n}\rangle }^q/J_{\langle 2^{n}\rangle }^{q+1}$
.
$J_{\langle 2^{n}\rangle }^q/J_{\langle 2^{n}\rangle }^{q+1}$
.
Let us show axiom v). To see that d satisfies the Leibniz rule, let
![]() $x\in J_{\langle 2^{n}\rangle }^q/J_{\langle 2^{n}\rangle }^{q+1}$
and
$x\in J_{\langle 2^{n}\rangle }^q/J_{\langle 2^{n}\rangle }^{q+1}$
and
![]() $y\in J_{\langle 2^{n}\rangle }^{q^{\prime }}/J_{\langle 2^{n}\rangle }^{q^{\prime }+1}$
, and let us calculate
$y\in J_{\langle 2^{n}\rangle }^{q^{\prime }}/J_{\langle 2^{n}\rangle }^{q^{\prime }+1}$
, and let us calculate
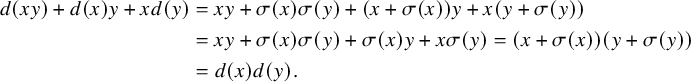 $$ \begin{align*} d(xy)+d(x) y+xd(y)&=xy+\sigma(x)\sigma(y)+(x+\sigma(x)) y+x(y+\sigma(y))\\ &=xy+\sigma(x)\sigma(y)+\sigma(x)y+x\sigma(y)=(x+\sigma(x)) (y+\sigma(y))\\ &=d(x)d(y). \end{align*} $$
$$ \begin{align*} d(xy)+d(x) y+xd(y)&=xy+\sigma(x)\sigma(y)+(x+\sigma(x)) y+x(y+\sigma(y))\\ &=xy+\sigma(x)\sigma(y)+\sigma(x)y+x\sigma(y)=(x+\sigma(x)) (y+\sigma(y))\\ &=d(x)d(y). \end{align*} $$
Since
![]() $d(x)$
belongs to
$d(x)$
belongs to
![]() $J_{\langle 2^{n}\rangle }^{q+1}$
and
$J_{\langle 2^{n}\rangle }^{q+1}$
and
![]() $d(y)$
to
$d(y)$
to
![]() $J_{\langle 2^{n}\rangle }^{q^{\prime }+1}$
by Proposition 3.1, we have that
$J_{\langle 2^{n}\rangle }^{q^{\prime }+1}$
by Proposition 3.1, we have that
![]() $d(x)d(y)$
belongs to
$d(x)d(y)$
belongs to
![]() $J_{\langle 2^{n}\rangle }^{q+q^{\prime }+2}$
, and therefore it vanishes in
$J_{\langle 2^{n}\rangle }^{q+q^{\prime }+2}$
, and therefore it vanishes in
![]() $J_{\langle 2^{n}\rangle }^{q+q^{\prime }+1}/J_{\langle 2^{n}\rangle }^{q+q^{\prime }+2}$
.
$J_{\langle 2^{n}\rangle }^{q+q^{\prime }+1}/J_{\langle 2^{n}\rangle }^{q+q^{\prime }+2}$
.
Let us now verify the last three identities involving d in axiom v). For the first one, let
![]() $x\in J_{\langle 2^{n}\rangle }^q/J_{\langle 2^{n}\rangle }^{q+1}$
. Then
$x\in J_{\langle 2^{n}\rangle }^q/J_{\langle 2^{n}\rangle }^{q+1}$
. Then
in
![]() $J_{\langle 2^{n}\rangle }^{q+1}/J_{\langle 2^{n}\rangle }^{q+2}$
, where
$J_{\langle 2^{n}\rangle }^{q+1}/J_{\langle 2^{n}\rangle }^{q+2}$
, where
![]() $F\sigma V(x)=0$
by the double coset formula (or by direct calculation). For the second identity, we have that
$F\sigma V(x)=0$
by the double coset formula (or by direct calculation). For the second identity, we have that
since
![]() $\sigma $
has order
$\sigma $
has order
![]() $2$
. Finally, for the third one, let
$2$
. Finally, for the third one, let
![]() $a\in k={\mathrm {W}}_{\langle 1\rangle }(k)$
. On the one hand, by Proposition 2.14,
$a\in k={\mathrm {W}}_{\langle 1\rangle }(k)$
. On the one hand, by Proposition 2.14,
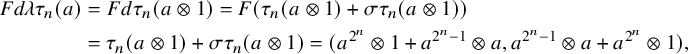 $$ \begin{align*} Fd\lambda\tau_n(a)&=Fd\tau_n(a\otimes 1)=F(\tau_n(a\otimes 1)+\sigma \tau_n(a\otimes 1)) \\&=\tau_n(a\otimes 1)+\sigma \tau_n(a\otimes 1)=(a^{2^{n}}\otimes 1+a^{2^{n}-1}\otimes a, a^{2^{n}-1}\otimes a+a^{2^{n}}\otimes 1), \end{align*} $$
$$ \begin{align*} Fd\lambda\tau_n(a)&=Fd\tau_n(a\otimes 1)=F(\tau_n(a\otimes 1)+\sigma \tau_n(a\otimes 1)) \\&=\tau_n(a\otimes 1)+\sigma \tau_n(a\otimes 1)=(a^{2^{n}}\otimes 1+a^{2^{n}-1}\otimes a, a^{2^{n}-1}\otimes a+a^{2^{n}}\otimes 1), \end{align*} $$
where the third equality holds by the formula for F of Theorem 2.7. On the other hand,
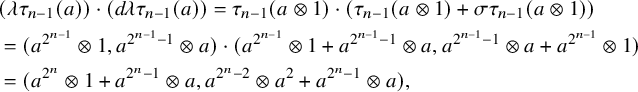 $$ \begin{align*} &(\lambda\tau_{n-1}(a))\cdot (d\lambda\tau_{n-1}(a))=\tau_{n-1}(a\otimes 1)\cdot (\tau_{n-1}(a\otimes 1)+\sigma\tau_{n-1}(a\otimes 1)) \\&=(a^{2^{n-1}}\otimes 1, a^{2^{n-1}-1}\otimes a)\cdot (a^{2^{n-1}}\otimes 1+a^{2^{n-1}-1}\otimes a, a^{2^{n-1}-1}\otimes a+a^{2^{n-1}}\otimes 1) \\&=(a^{2^{n}}\otimes 1+a^{2^{n}-1}\otimes a, a^{2^{n}-2}\otimes a^2+a^{2^{n}-1}\otimes a), \end{align*} $$
$$ \begin{align*} &(\lambda\tau_{n-1}(a))\cdot (d\lambda\tau_{n-1}(a))=\tau_{n-1}(a\otimes 1)\cdot (\tau_{n-1}(a\otimes 1)+\sigma\tau_{n-1}(a\otimes 1)) \\&=(a^{2^{n-1}}\otimes 1, a^{2^{n-1}-1}\otimes a)\cdot (a^{2^{n-1}}\otimes 1+a^{2^{n-1}-1}\otimes a, a^{2^{n-1}-1}\otimes a+a^{2^{n-1}}\otimes 1) \\&=(a^{2^{n}}\otimes 1+a^{2^{n}-1}\otimes a, a^{2^{n}-2}\otimes a^2+a^{2^{n}-1}\otimes a), \end{align*} $$
and these are equal since we are tensoring over S.
3.2 The Milnor conjecture for the de Rham-Witt complex
Let us endow the sequence
![]() $J_{\langle 2^\bullet \rangle }^\ast /J_{\langle 2^\bullet \rangle }^{\ast +1}$
with the structure of a
$J_{\langle 2^\bullet \rangle }^\ast /J_{\langle 2^\bullet \rangle }^{\ast +1}$
with the structure of a
![]() $2$
-typical Witt complex of Proposition 3.3. We recall that, by definition, the
$2$
-typical Witt complex of Proposition 3.3. We recall that, by definition, the
![]() $2$
-typical de Rham-Witt complex
$2$
-typical de Rham-Witt complex
![]() ${\mathrm {W}}_{\langle 2^\bullet \rangle }\Omega ^\ast _k$
of k is the initial object in the category of
${\mathrm {W}}_{\langle 2^\bullet \rangle }\Omega ^\ast _k$
of k is the initial object in the category of
![]() $2$
-typical Witt complexes over k (see [Reference CosteanuCos08] and [Reference Hesselholt and MadsenHM04]). Thus, there is a unique map of
$2$
-typical Witt complexes over k (see [Reference CosteanuCos08] and [Reference Hesselholt and MadsenHM04]). Thus, there is a unique map of
![]() $2$
-typical Witt complexes
$2$
-typical Witt complexes
Let us denote by
![]() ${\mathrm {W}}_{\langle 2^\bullet \rangle }\Omega ^\ast _k/2$
the degreewise cokernel of the multiplication by
${\mathrm {W}}_{\langle 2^\bullet \rangle }\Omega ^\ast _k/2$
the degreewise cokernel of the multiplication by
![]() $2$
map. Since all the maps defining the structure of a Witt complex are additive, this is again a Witt-complex, where the map
$2$
map. Since all the maps defining the structure of a Witt complex are additive, this is again a Witt-complex, where the map
is the quotient map. Since
![]() $2$
vanishes in
$2$
vanishes in
![]() $J_{\langle 2^\bullet \rangle }^\ast /J_{\langle 2^\bullet \rangle }^{\ast +1}$
, the unique map above descends to a unique map of Witt-complexes
$J_{\langle 2^\bullet \rangle }^\ast /J_{\langle 2^\bullet \rangle }^{\ast +1}$
, the unique map above descends to a unique map of Witt-complexes
Theorem 3.4. The unique map of Witt-complexes
![]() $u\colon {\mathrm {W}}_{\langle 2^\bullet \rangle }\Omega ^\ast _k/2\to J_{\langle 2^\bullet \rangle }^\ast /J_{\langle 2^\bullet \rangle }^{\ast +1}$
is an isomorphism.
$u\colon {\mathrm {W}}_{\langle 2^\bullet \rangle }\Omega ^\ast _k/2\to J_{\langle 2^\bullet \rangle }^\ast /J_{\langle 2^\bullet \rangle }^{\ast +1}$
is an isomorphism.
Remark 3.5. Let us discuss a few special cases of this theorem. For
![]() $\ast =0$
, the unique map u is by construction the isomorphism
$\ast =0$
, the unique map u is by construction the isomorphism
where the arrow is the isomorphism of [Reference Hesselholt and MadsenHM97, Theorem F].
However, for
![]() $\bullet =0$
, the map u is the unique map of commutative differential graded algebras
$\bullet =0$
, the map u is the unique map of commutative differential graded algebras
This is well known to be an isomorphism, as claimed in [Reference KatoKat82] (see, for example, [Reference ArasonAra20] for a proof, which is also recasted in Lemma 3.6 below). In particular, for
![]() $\ast =1$
, this is equivalent to the fact that since k has characteristic
$\ast =1$
, this is equivalent to the fact that since k has characteristic
![]() $2$
, a
$2$
, a
![]() $\mathbb {Z}$
-linear derivation out of k is automatically S-linear (where we recall that
$\mathbb {Z}$
-linear derivation out of k is automatically S-linear (where we recall that
![]() $S\leq k$
is the subfield of squares).
$S\leq k$
is the subfield of squares).
The rest of the section is dedicated to the proof of Theorem 3.4. The proof is by induction on n, by means of the exact sequences
from [Reference CosteanuCos08, Lemma 3.5], where
![]() $n, q\geq 1$
.
$n, q\geq 1$
.
The base case for the induction
![]() $n=1$
seems to be well known to the experts and is used without proof in [Reference KatoKat82]. We recall the argument from [Reference ArasonAra20, Fact 1] for the reader’s convenience, and to introduce some notation that we will use in the proof of the induction step.
$n=1$
seems to be well known to the experts and is used without proof in [Reference KatoKat82]. We recall the argument from [Reference ArasonAra20, Fact 1] for the reader’s convenience, and to introduce some notation that we will use in the proof of the induction step.
Lemma 3.6 [Reference ArasonAra20]
The unique map
![]() $u\colon \Omega ^\ast _k\longrightarrow J_{\langle 1\rangle }^\ast /J_{\langle 1\rangle }^{\ast +1}$
of commutative differential graded algebras is an isomorphism.
$u\colon \Omega ^\ast _k\longrightarrow J_{\langle 1\rangle }^\ast /J_{\langle 1\rangle }^{\ast +1}$
of commutative differential graded algebras is an isomorphism.
Proof. For every
![]() $a\in k$
, let us denote
$a\in k$
, let us denote
![]() $\Delta (a):=1\otimes a+a\otimes 1\in k\otimes _S k$
. We note that the map u is necessarily given by the formula
$\Delta (a):=1\otimes a+a\otimes 1\in k\otimes _S k$
. We note that the map u is necessarily given by the formula
In order to show that this is an isomorphism, we choose suitable bases of the source and target as k-vector spaces. Let
![]() $\{x_{i}\}_{i\in I}$
be a
$\{x_{i}\}_{i\in I}$
be a
![]() $2$
-basis of k. We recall that this is a set of elements of k whose differentials
$2$
-basis of k. We recall that this is a set of elements of k whose differentials
![]() $\{dx_i\}_{i\in I}$
form a basis of the k-vector space
$\{dx_i\}_{i\in I}$
form a basis of the k-vector space
![]() $\Omega ^1_k$
or, equivalently, such that the elements
$\Omega ^1_k$
or, equivalently, such that the elements
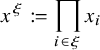 $$\begin{align*}x^\xi:=\prod_{i\in \xi}x_i \end{align*}$$
$$\begin{align*}x^\xi:=\prod_{i\in \xi}x_i \end{align*}$$
form a basis of k as an S-vector space, where
![]() $\xi $
ranges through the finite subsets of I (see [Reference GrothendieckGro67, Chapter 0, §21.4]). Here, we use the convention that
$\xi $
ranges through the finite subsets of I (see [Reference GrothendieckGro67, Chapter 0, §21.4]). Here, we use the convention that
![]() $x^\emptyset =1$
, and we will write
$x^\emptyset =1$
, and we will write
![]() $\xi \subset ^f \! I$
if
$\xi \subset ^f \! I$
if
![]() $\xi $
is a finite subset of I. It is easy to see that the set
$\xi $
is a finite subset of I. It is easy to see that the set
![]() $\{1\otimes x^\xi \}_{\xi \subset ^f I}$
is a basis of
$\{1\otimes x^\xi \}_{\xi \subset ^f I}$
is a basis of
![]() $k\otimes _S k$
as a k-vector space, where k acts by multiplication on the left tensor factor. Now let us denote
$k\otimes _S k$
as a k-vector space, where k acts by multiplication on the left tensor factor. Now let us denote
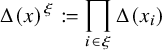 $$\begin{align*}\Delta(x)^{\xi}:=\prod_{i\in \xi}\Delta(x_i) \end{align*}$$
$$\begin{align*}\Delta(x)^{\xi}:=\prod_{i\in \xi}\Delta(x_i) \end{align*}$$
for every
![]() $\xi \subset ^f\! I$
(with the convention that
$\xi \subset ^f\! I$
(with the convention that
![]() $\Delta (x)^{\emptyset }=1\otimes 1$
). These elements satisfy the identities
$\Delta (x)^{\emptyset }=1\otimes 1$
). These elements satisfy the identities
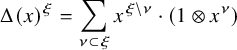 $$ \begin{align} \Delta(x)^{\xi}&=\sum_{\nu\subset\xi}x^{\xi\setminus\nu}\cdot(1\otimes x^\nu) \end{align} $$
$$ \begin{align} \Delta(x)^{\xi}&=\sum_{\nu\subset\xi}x^{\xi\setminus\nu}\cdot(1\otimes x^\nu) \end{align} $$
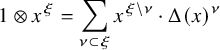 $$ \begin{align} 1\otimes x^{\xi}&=\sum_{\nu\subset\xi}x^{\xi\setminus\nu}\cdot\Delta(x)^{\nu} \end{align} $$
$$ \begin{align} 1\otimes x^{\xi}&=\sum_{\nu\subset\xi}x^{\xi\setminus\nu}\cdot\Delta(x)^{\nu} \end{align} $$
for every finite subset
![]() $\xi $
of I. It follows that
$\xi $
of I. It follows that
![]() $\{\Delta (x)^{\xi }\}_{\xi \subset ^f I}$
is also a basis of
$\{\Delta (x)^{\xi }\}_{\xi \subset ^f I}$
is also a basis of
![]() $k\otimes _S k$
. Since the multiplication map sends
$k\otimes _S k$
. Since the multiplication map sends
![]() $\Delta (x)^{\xi }$
to a nonzero element of k if and only if
$\Delta (x)^{\xi }$
to a nonzero element of k if and only if
![]() $\xi =\emptyset $
, it follows that
$\xi =\emptyset $
, it follows that
![]() $\{\Delta (x)^{\xi }\}_{\emptyset \neq \xi \subset ^f I}$
is a basis for
$\{\Delta (x)^{\xi }\}_{\emptyset \neq \xi \subset ^f I}$
is a basis for
![]() $J_{\langle 1\rangle }$
as a k-vector space with respect to multiplication on the left factor. It then readily follows that the elements
$J_{\langle 1\rangle }$
as a k-vector space with respect to multiplication on the left factor. It then readily follows that the elements
![]() $\Delta (x)^{\xi }$
with
$\Delta (x)^{\xi }$
with
![]() $|\xi |\geq q$
form a basis of
$|\xi |\geq q$
form a basis of
![]() $J_{\langle 1\rangle }^q$
, and that the elements
$J_{\langle 1\rangle }^q$
, and that the elements
![]() $\Delta (x)^{\xi }$
with
$\Delta (x)^{\xi }$
with
![]() $|\xi |= q$
form a basis of
$|\xi |= q$
form a basis of
![]() $J_{\langle 1\rangle }^q/J_{\langle 1\rangle }^{q+1}$
. Since for every
$J_{\langle 1\rangle }^q/J_{\langle 1\rangle }^{q+1}$
. Since for every
![]() $\xi \subset I$
with
$\xi \subset I$
with
![]() $|\xi |=q$
, the map u sends a basis element
$|\xi |=q$
, the map u sends a basis element
![]() $(dx)^\xi :=\prod _{i\in \xi }dx_i$
of
$(dx)^\xi :=\prod _{i\in \xi }dx_i$
of
![]() $\Omega ^q_k$
to
$\Omega ^q_k$
to
![]() $\Delta (x)^{\xi }$
, the claim follows.
$\Delta (x)^{\xi }$
, the claim follows.
The induction step for proving Theorem 3.4 will rely on the following two key technical Lemmas. Let us choose a
![]() $2$
-basis
$2$
-basis
![]() $\{x_{i}\}_{i\in I}$
of k as in the proof of Lemma 3.6.
$\{x_{i}\}_{i\in I}$
of k as in the proof of Lemma 3.6.
Lemma 3.7. Let
![]() $q\geq 1$
, and let
$q\geq 1$
, and let
![]() $\mu _\nu \in k$
for every subset
$\mu _\nu \in k$
for every subset
![]() $\nu \subset I$
with
$\nu \subset I$
with
![]() $|\nu |=q-1$
. Suppose that
$|\nu |=q-1$
. Suppose that
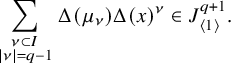 $$\begin{align*}\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} }\Delta(\mu_\nu)\Delta(x)^{\nu} \in J_{\langle 1 \rangle}^{q+1}.\end{align*}$$
$$\begin{align*}\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} }\Delta(\mu_\nu)\Delta(x)^{\nu} \in J_{\langle 1 \rangle}^{q+1}.\end{align*}$$
Then
![]() $\sum _{\nu \subset I, |\nu |=q-1}V(\mu _\nu (dx)^\nu )$
is divisible by
$\sum _{\nu \subset I, |\nu |=q-1}V(\mu _\nu (dx)^\nu )$
is divisible by
![]() $2$
in
$2$
in
![]() ${\mathrm {W}}_{\langle 2\rangle }\Omega ^{q-1}_k$
.
${\mathrm {W}}_{\langle 2\rangle }\Omega ^{q-1}_k$
.
Proof. Let us write
![]() $\mu _\nu \in k$
uniquely as a linear combination
$\mu _\nu \in k$
uniquely as a linear combination
![]() $\mu _\nu =\sum _{\delta \subset ^f I}s_{\nu , \delta }^2x^\delta $
with respect to the basis
$\mu _\nu =\sum _{\delta \subset ^f I}s_{\nu , \delta }^2x^\delta $
with respect to the basis
![]() $\{x^\delta \}_{\delta \subset ^f I}$
of k as an S-vector space. Let us notice that, since we are tensoring over S, the map
$\{x^\delta \}_{\delta \subset ^f I}$
of k as an S-vector space. Let us notice that, since we are tensoring over S, the map
![]() $\Delta \colon k\to k\otimes _Sk$
is S-linear. Then by applying formula (3.2),
$\Delta \colon k\to k\otimes _Sk$
is S-linear. Then by applying formula (3.2),
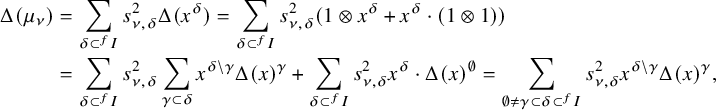 $$ \begin{align*} \Delta(\mu_\nu)&=\sum_{\delta\subset^f I}s_{\nu, \delta}^2\Delta(x^\delta)=\sum_{\delta\subset^f I}s_{\nu, \delta}^2(1\otimes x^\delta+x^{\delta}\cdot (1\otimes 1)) \\ &=\sum_{\delta\subset^f I}s_{\nu, \delta}^2\sum_{\gamma\subset\delta}x^{\delta\setminus \gamma}\Delta(x)^\gamma+\sum_{\delta\subset^f I}s_{\nu, \delta}^2x^{\delta}\cdot \Delta(x)^{\emptyset} =\sum_{\emptyset\neq \gamma\subset\delta\subset^f I}s_{\nu, \delta}^2x^{\delta\setminus \gamma}\Delta(x)^\gamma, \end{align*} $$
$$ \begin{align*} \Delta(\mu_\nu)&=\sum_{\delta\subset^f I}s_{\nu, \delta}^2\Delta(x^\delta)=\sum_{\delta\subset^f I}s_{\nu, \delta}^2(1\otimes x^\delta+x^{\delta}\cdot (1\otimes 1)) \\ &=\sum_{\delta\subset^f I}s_{\nu, \delta}^2\sum_{\gamma\subset\delta}x^{\delta\setminus \gamma}\Delta(x)^\gamma+\sum_{\delta\subset^f I}s_{\nu, \delta}^2x^{\delta}\cdot \Delta(x)^{\emptyset} =\sum_{\emptyset\neq \gamma\subset\delta\subset^f I}s_{\nu, \delta}^2x^{\delta\setminus \gamma}\Delta(x)^\gamma, \end{align*} $$
where the last equality holds since the sum
![]() $\sum _{\delta \subset ^f I}s_{\nu , \delta }^2x^{\delta }\cdot \Delta (x)^{\emptyset }$
is equal to the term
$\sum _{\delta \subset ^f I}s_{\nu , \delta }^2x^{\delta }\cdot \Delta (x)^{\emptyset }$
is equal to the term
![]() $\gamma =\emptyset $
in the previous sum. It follows that
$\gamma =\emptyset $
in the previous sum. It follows that
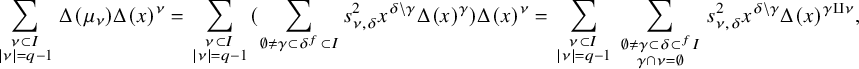 $$ \begin{align*} \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} }\Delta(\mu_\nu)\Delta(x)^{\nu} &=\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } (\sum_{\emptyset\neq \gamma\subset\delta^f\subset I}s_{\nu, \delta}^2x^{\delta\setminus \gamma}\Delta(x)^\gamma)\Delta(x)^{\nu} =\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } \sum_{ \begin{smallmatrix} \emptyset\neq \gamma\subset\delta\subset^f I \\ \gamma\cap\nu=\emptyset \end{smallmatrix} }s_{\nu, \delta}^2x^{\delta\setminus \gamma}\Delta(x)^{\gamma\amalg\nu}, \end{align*} $$
$$ \begin{align*} \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} }\Delta(\mu_\nu)\Delta(x)^{\nu} &=\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } (\sum_{\emptyset\neq \gamma\subset\delta^f\subset I}s_{\nu, \delta}^2x^{\delta\setminus \gamma}\Delta(x)^\gamma)\Delta(x)^{\nu} =\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } \sum_{ \begin{smallmatrix} \emptyset\neq \gamma\subset\delta\subset^f I \\ \gamma\cap\nu=\emptyset \end{smallmatrix} }s_{\nu, \delta}^2x^{\delta\setminus \gamma}\Delta(x)^{\gamma\amalg\nu}, \end{align*} $$
where in the last sum
![]() $\gamma $
and
$\gamma $
and
![]() $\nu $
are disjoint, since
$\nu $
are disjoint, since
![]() $\Delta (a)\Delta (a)=0$
in
$\Delta (a)\Delta (a)=0$
in
![]() $k\otimes _Sk$
for all
$k\otimes _Sk$
for all
![]() $a\in k$
. Since, by assumption, this element belongs to
$a\in k$
. Since, by assumption, this element belongs to
![]() $J_{\langle 1 \rangle }^{q+1}$
, and the
$J_{\langle 1 \rangle }^{q+1}$
, and the
![]() $\Delta (x)^\xi $
with
$\Delta (x)^\xi $
with
![]() $|\xi |=q+1$
are a basis for
$|\xi |=q+1$
are a basis for
![]() $ J_{\langle 1 \rangle }^{q+1}$
, we must have that, for every
$ J_{\langle 1 \rangle }^{q+1}$
, we must have that, for every
![]() $\nu \subset I$
with
$\nu \subset I$
with
![]() $|\nu |=q-1$
and every
$|\nu |=q-1$
and every
![]() $j\in I\setminus \nu $
(corresponding to the terms
$j\in I\setminus \nu $
(corresponding to the terms
![]() $\gamma =\{j\}$
in the sum above),
$\gamma =\{j\}$
in the sum above),
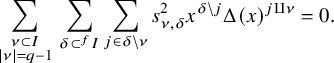 $$\begin{align*}\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } \sum_{\delta\subset^f I}\sum_{ j\in \delta\setminus\nu } s_{\nu, \delta}^2x^{\delta\setminus j}\Delta(x)^{j\amalg\nu} =0. \end{align*}$$
$$\begin{align*}\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } \sum_{\delta\subset^f I}\sum_{ j\in \delta\setminus\nu } s_{\nu, \delta}^2x^{\delta\setminus j}\Delta(x)^{j\amalg\nu} =0. \end{align*}$$
Since the
![]() $\Delta (x)^{\xi }$
are linearly independent, we have that, for every subset
$\Delta (x)^{\xi }$
are linearly independent, we have that, for every subset
![]() $\xi \subset I$
with
$\xi \subset I$
with
![]() $|\xi |=q$
(corresponding to the terms
$|\xi |=q$
(corresponding to the terms
![]() $\epsilon =j\amalg \nu $
), the coefficient of
$\epsilon =j\amalg \nu $
), the coefficient of
![]() $\Delta (x)^{\xi }$
must vanish – that is, that
$\Delta (x)^{\xi }$
must vanish – that is, that
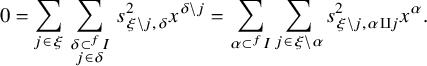 $$\begin{align*}0=\sum_{j\in \xi} \sum_{ \begin{smallmatrix} \delta\subset^f I \\ j\in \delta \end{smallmatrix} } s_{\xi\setminus j, \delta}^2x^{\delta\setminus j} = \sum_{\alpha\subset^f I} \sum_{ j\in \xi\setminus \alpha } s_{\xi\setminus j, \alpha\amalg j}^2x^{\alpha}. \end{align*}$$
$$\begin{align*}0=\sum_{j\in \xi} \sum_{ \begin{smallmatrix} \delta\subset^f I \\ j\in \delta \end{smallmatrix} } s_{\xi\setminus j, \delta}^2x^{\delta\setminus j} = \sum_{\alpha\subset^f I} \sum_{ j\in \xi\setminus \alpha } s_{\xi\setminus j, \alpha\amalg j}^2x^{\alpha}. \end{align*}$$
Since the
![]() $x^{\alpha }$
form a basis of k as an S-vector space, we find that for every finite
$x^{\alpha }$
form a basis of k as an S-vector space, we find that for every finite
![]() $\alpha \subset I$
and
$\alpha \subset I$
and
![]() $\xi \subset I$
with
$\xi \subset I$
with
![]() $|\xi |=q$
, the corresponding coefficient must vanish:
$|\xi |=q$
, the corresponding coefficient must vanish:
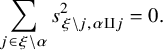 $$ \begin{align} \sum_{ j\in \xi\setminus \alpha } s_{\xi\setminus j, \alpha\amalg j}^2=0. \end{align} $$
$$ \begin{align} \sum_{ j\in \xi\setminus \alpha } s_{\xi\setminus j, \alpha\amalg j}^2=0. \end{align} $$
We now show that these relations among the coefficients
![]() $s_{\nu , \delta }$
imply that
$s_{\nu , \delta }$
imply that
![]() $V(\sum _{\nu \subset I, |\nu |=q-1}\mu _\nu (dx)^\nu )$
is divisible by
$V(\sum _{\nu \subset I, |\nu |=q-1}\mu _\nu (dx)^\nu )$
is divisible by
![]() $2$
in
$2$
in
![]() ${\mathrm {W}}_{\langle 2\rangle }\Omega ^{q-1}_k$
. We do this by showing that the sum
${\mathrm {W}}_{\langle 2\rangle }\Omega ^{q-1}_k$
. We do this by showing that the sum
![]() $\sum _{\nu \subset I, |\nu |=q-1}\mu _\nu (dx)^\nu $
is in the image of the Frobenius map. The claim will then follow since, by the linearity of V of axiom iv) of Definition 3.2,
$\sum _{\nu \subset I, |\nu |=q-1}\mu _\nu (dx)^\nu $
is in the image of the Frobenius map. The claim will then follow since, by the linearity of V of axiom iv) of Definition 3.2,
for every
![]() $z\in {\mathrm {W}}_{\langle 2\rangle }\Omega ^{q-1}_k$
, and
$z\in {\mathrm {W}}_{\langle 2\rangle }\Omega ^{q-1}_k$
, and
![]() $V(1)=2\in {\mathrm {W}}_{\langle 2\rangle }(k)$
since k has characteristic
$V(1)=2\in {\mathrm {W}}_{\langle 2\rangle }(k)$
since k has characteristic
![]() $2$
.
$2$
.
By rearranging the terms and grouping pairs
![]() $(\nu , \delta )$
with the same intersection
$(\nu , \delta )$
with the same intersection
![]() $\beta $
, we can write
$\beta $
, we can write
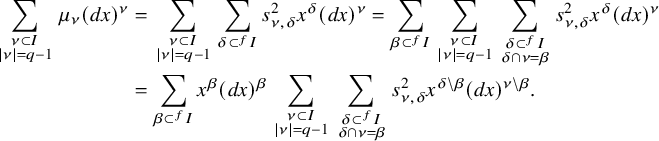 $$ \begin{align} \begin{split} \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } \mu_\nu (dx)^\nu &= \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } \sum_{\delta\subset^f I}s^2_{\nu, \delta}x^{\delta} (dx)^\nu = \sum_{\beta\subset^f I} \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } \sum_{ \begin{smallmatrix} \delta\subset^f I \\ \delta\cap\nu=\beta \end{smallmatrix} } s^2_{\nu, \delta}x^{\delta} (dx)^\nu \\&= \sum_{\beta\subset^f I} x^{\beta} (dx)^\beta \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } \sum_{ \begin{smallmatrix} \delta\subset^f I \\ \delta\cap\nu=\beta \end{smallmatrix} } s^2_{\nu, \delta}x^{\delta\setminus\beta} (dx)^{\nu\setminus\beta}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } \mu_\nu (dx)^\nu &= \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } \sum_{\delta\subset^f I}s^2_{\nu, \delta}x^{\delta} (dx)^\nu = \sum_{\beta\subset^f I} \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } \sum_{ \begin{smallmatrix} \delta\subset^f I \\ \delta\cap\nu=\beta \end{smallmatrix} } s^2_{\nu, \delta}x^{\delta} (dx)^\nu \\&= \sum_{\beta\subset^f I} x^{\beta} (dx)^\beta \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } \sum_{ \begin{smallmatrix} \delta\subset^f I \\ \delta\cap\nu=\beta \end{smallmatrix} } s^2_{\nu, \delta}x^{\delta\setminus\beta} (dx)^{\nu\setminus\beta}. \end{split} \end{align} $$
Each term
![]() $x^{\beta } (dx)^\beta $
is in the image of the Frobenius, since by axiom v) of Definition 3.2 (we recall that in the de Rham-Witt complex the map
$x^{\beta } (dx)^\beta $
is in the image of the Frobenius, since by axiom v) of Definition 3.2 (we recall that in the de Rham-Witt complex the map
![]() $\lambda $
is the identity),
$\lambda $
is the identity),
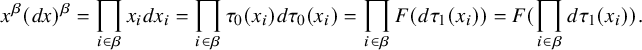 $$ \begin{align*} x^\beta(dx)^\beta&=\prod_{i\in\beta}x_idx_i=\prod_{i\in\beta}\tau_0(x_i)d\tau_0(x_i)=\prod_{i\in\beta}F(d\tau_1(x_i))=F(\prod_{i\in\beta}d\tau_1(x_i)). \end{align*} $$
$$ \begin{align*} x^\beta(dx)^\beta&=\prod_{i\in\beta}x_idx_i=\prod_{i\in\beta}\tau_0(x_i)d\tau_0(x_i)=\prod_{i\in\beta}F(d\tau_1(x_i))=F(\prod_{i\in\beta}d\tau_1(x_i)). \end{align*} $$
It is therefore sufficient to show that for every fixed
![]() $\beta \subset I$
, the double sum in equation (3.4) is in the image of the Frobenius. Let us now group those terms by the union
$\beta \subset I$
, the double sum in equation (3.4) is in the image of the Frobenius. Let us now group those terms by the union
![]() $\lambda $
of
$\lambda $
of
![]() $\nu $
and
$\nu $
and
![]() $\delta $
, and write
$\delta $
, and write
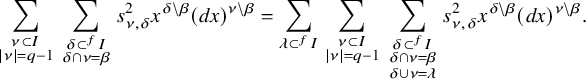 $$ \begin{align} \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } \sum_{ \begin{smallmatrix} \delta\subset^f I \\ \delta\cap\nu=\beta \end{smallmatrix} } s^2_{\nu, \delta}x^{\delta\setminus\beta} (dx)^{\nu\setminus\beta} &= \sum_{\lambda\subset^f I} \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } \sum_{ \begin{smallmatrix} \delta\subset^f I \\ \delta\cap\nu=\beta \\ \delta\cup \nu=\lambda \end{smallmatrix} } s^2_{\nu, \delta}x^{\delta\setminus\beta} (dx)^{\nu\setminus\beta}. \end{align} $$
$$ \begin{align} \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } \sum_{ \begin{smallmatrix} \delta\subset^f I \\ \delta\cap\nu=\beta \end{smallmatrix} } s^2_{\nu, \delta}x^{\delta\setminus\beta} (dx)^{\nu\setminus\beta} &= \sum_{\lambda\subset^f I} \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } \sum_{ \begin{smallmatrix} \delta\subset^f I \\ \delta\cap\nu=\beta \\ \delta\cup \nu=\lambda \end{smallmatrix} } s^2_{\nu, \delta}x^{\delta\setminus\beta} (dx)^{\nu\setminus\beta}. \end{align} $$
We now show that for every fixed
![]() $\beta , \lambda \subset ^f I$
, the inner double sum in (3.5) is in the image of the Frobenius. Notice that, after fixing
$\beta , \lambda \subset ^f I$
, the inner double sum in (3.5) is in the image of the Frobenius. Notice that, after fixing
![]() $\beta $
and
$\beta $
and
![]() $\lambda $
, the subset
$\lambda $
, the subset
![]() $\delta $
is determined by
$\delta $
is determined by
![]() $\nu $
, and let us write
$\nu $
, and let us write
![]() $\delta _\nu :=(\lambda \setminus \nu )\amalg \beta $
. That is, we show that
$\delta _\nu :=(\lambda \setminus \nu )\amalg \beta $
. That is, we show that
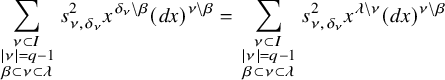 $$ \begin{align} \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \end{smallmatrix} } s^2_{\nu, \delta_\nu}x^{\delta_\nu\setminus\beta} (dx)^{\nu\setminus\beta}=\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \end{smallmatrix} } s^2_{\nu, \delta_\nu}x^{\lambda\setminus \nu} (dx)^{\nu\setminus\beta} \end{align} $$
$$ \begin{align} \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \end{smallmatrix} } s^2_{\nu, \delta_\nu}x^{\delta_\nu\setminus\beta} (dx)^{\nu\setminus\beta}=\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \end{smallmatrix} } s^2_{\nu, \delta_\nu}x^{\lambda\setminus \nu} (dx)^{\nu\setminus\beta} \end{align} $$
is in the image of the Frobenius. Let us first treat the case where
![]() $\beta =\lambda $
(with
$\beta =\lambda $
(with
![]() $q-1$
elements, otherwise the sum is trivially zero). In this case, the sum is just
$q-1$
elements, otherwise the sum is trivially zero). In this case, the sum is just
![]() $s^2_{\beta , \beta }$
, and every square of k is in the image of the Frobenius since
$s^2_{\beta , \beta }$
, and every square of k is in the image of the Frobenius since
![]() $s^2=F(\tau _1(s))$
. Thus, suppose that
$s^2=F(\tau _1(s))$
. Thus, suppose that
![]() $\beta $
is a proper subset of
$\beta $
is a proper subset of
![]() $\lambda $
, and choose an element
$\lambda $
, and choose an element
![]() $j_0\in \lambda \setminus \beta $
. We claim that (3.6) is equal to
$j_0\in \lambda \setminus \beta $
. We claim that (3.6) is equal to
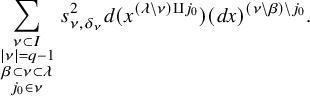 $$\begin{align*}\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \\ j_0\in\nu \end{smallmatrix} } s^2_{\nu, \delta_\nu}d(x^{(\lambda\setminus \nu)\amalg j_0})(dx)^{(\nu\setminus\beta)\setminus j_0}. \end{align*}$$
$$\begin{align*}\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \\ j_0\in\nu \end{smallmatrix} } s^2_{\nu, \delta_\nu}d(x^{(\lambda\setminus \nu)\amalg j_0})(dx)^{(\nu\setminus\beta)\setminus j_0}. \end{align*}$$
This will conclude the proof, since any square is in the image of the Frobenius by the argument above, and so is each differential by the relation
![]() $d=FdV$
of axiom v) (observe that
$d=FdV$
of axiom v) (observe that
![]() $\lambda \setminus \nu $
and
$\lambda \setminus \nu $
and
![]() $\nu \setminus \beta $
are disjoint, with union
$\nu \setminus \beta $
are disjoint, with union
![]() $\lambda \setminus \beta $
, so that no summands contain the square of a differential). To see that the last claim holds, let us notice that by iterating the Leibniz rule,
$\lambda \setminus \beta $
, so that no summands contain the square of a differential). To see that the last claim holds, let us notice that by iterating the Leibniz rule,
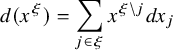 $$\begin{align*}d(x^{\xi})=\sum_{j\in\xi}x^{\xi\setminus j}dx_j \end{align*}$$
$$\begin{align*}d(x^{\xi})=\sum_{j\in\xi}x^{\xi\setminus j}dx_j \end{align*}$$
for every finite subset
![]() $\xi \subset I$
, and therefore
$\xi \subset I$
, and therefore
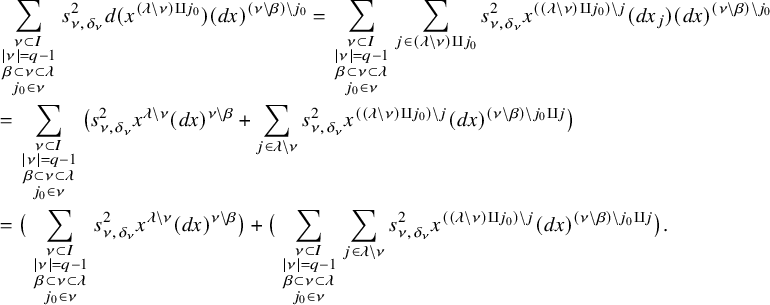 $$ \begin{align*} &\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \\ j_0\in\nu \end{smallmatrix} } s^2_{\nu, \delta_\nu}d(x^{(\lambda\setminus \nu)\amalg j_0})(dx)^{(\nu\setminus\beta)\setminus j_0} = \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \\ j_0\in\nu \end{smallmatrix} } \sum_{j\in (\lambda\setminus \nu)\amalg j_0} s^2_{\nu, \delta_\nu}x^{((\lambda\setminus \nu)\amalg j_0)\setminus j}(dx_{j})(dx)^{(\nu\setminus\beta)\setminus j_0} \\ &= \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \\ j_0\in\nu \end{smallmatrix} } \big( s^2_{\nu, \delta_\nu}x^{\lambda\setminus \nu}(dx)^{\nu\setminus\beta} + \sum_{j\in \lambda\setminus \nu} s^2_{\nu, \delta_\nu}x^{((\lambda\setminus \nu)\amalg j_0)\setminus j}(dx)^{(\nu\setminus\beta)\setminus j_0\amalg j} \big) \\ &= \big(\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \\ j_0\in\nu \end{smallmatrix} } s^2_{\nu, \delta_\nu}x^{\lambda\setminus \nu}(dx)^{\nu\setminus\beta} \big) + \big(\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \\ j_0\in\nu \end{smallmatrix} } \sum_{j\in \lambda\setminus \nu} s^2_{\nu, \delta_\nu}x^{((\lambda\setminus \nu)\amalg j_0)\setminus j}(dx)^{(\nu\setminus\beta)\setminus j_0\amalg j} \big). \end{align*} $$
$$ \begin{align*} &\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \\ j_0\in\nu \end{smallmatrix} } s^2_{\nu, \delta_\nu}d(x^{(\lambda\setminus \nu)\amalg j_0})(dx)^{(\nu\setminus\beta)\setminus j_0} = \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \\ j_0\in\nu \end{smallmatrix} } \sum_{j\in (\lambda\setminus \nu)\amalg j_0} s^2_{\nu, \delta_\nu}x^{((\lambda\setminus \nu)\amalg j_0)\setminus j}(dx_{j})(dx)^{(\nu\setminus\beta)\setminus j_0} \\ &= \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \\ j_0\in\nu \end{smallmatrix} } \big( s^2_{\nu, \delta_\nu}x^{\lambda\setminus \nu}(dx)^{\nu\setminus\beta} + \sum_{j\in \lambda\setminus \nu} s^2_{\nu, \delta_\nu}x^{((\lambda\setminus \nu)\amalg j_0)\setminus j}(dx)^{(\nu\setminus\beta)\setminus j_0\amalg j} \big) \\ &= \big(\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \\ j_0\in\nu \end{smallmatrix} } s^2_{\nu, \delta_\nu}x^{\lambda\setminus \nu}(dx)^{\nu\setminus\beta} \big) + \big(\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \\ j_0\in\nu \end{smallmatrix} } \sum_{j\in \lambda\setminus \nu} s^2_{\nu, \delta_\nu}x^{((\lambda\setminus \nu)\amalg j_0)\setminus j}(dx)^{(\nu\setminus\beta)\setminus j_0\amalg j} \big). \end{align*} $$
By setting
![]() $\zeta =(\nu \setminus j_0)\amalg j$
in the second sum, and observing that
$\zeta =(\nu \setminus j_0)\amalg j$
in the second sum, and observing that
![]() $\delta _\nu =(\delta _{\zeta }\setminus j_0)\amalg j$
, we find that this is equal to
$\delta _\nu =(\delta _{\zeta }\setminus j_0)\amalg j$
, we find that this is equal to
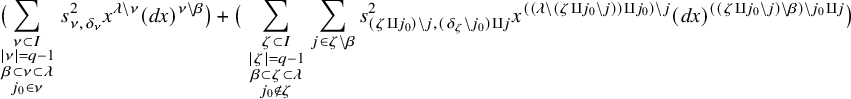 $$ \begin{align} &\big(\!\!\!\!\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \\ j_0\in\nu \end{smallmatrix} } s^2_{\nu, \delta_\nu}x^{\lambda\setminus \nu}(dx)^{\nu\setminus\beta} \big) + \big(\sum_{ \begin{smallmatrix} \zeta\subset I \\ |\zeta|=q-1 \\ \beta\subset\zeta\subset\lambda \\ j_0\notin\zeta \end{smallmatrix} } \sum_{j\in \zeta\setminus\beta} s^2_{(\zeta\amalg j_0)\setminus j, (\delta_{\zeta}\setminus j_0)\amalg j}x^{((\lambda\setminus (\zeta\amalg j_0\setminus j))\amalg j_0)\setminus j}(dx)^{((\zeta\amalg j_0\setminus j)\setminus\beta)\setminus j_0\amalg j} \big) \end{align} $$
$$ \begin{align} &\big(\!\!\!\!\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \\ j_0\in\nu \end{smallmatrix} } s^2_{\nu, \delta_\nu}x^{\lambda\setminus \nu}(dx)^{\nu\setminus\beta} \big) + \big(\sum_{ \begin{smallmatrix} \zeta\subset I \\ |\zeta|=q-1 \\ \beta\subset\zeta\subset\lambda \\ j_0\notin\zeta \end{smallmatrix} } \sum_{j\in \zeta\setminus\beta} s^2_{(\zeta\amalg j_0)\setminus j, (\delta_{\zeta}\setminus j_0)\amalg j}x^{((\lambda\setminus (\zeta\amalg j_0\setminus j))\amalg j_0)\setminus j}(dx)^{((\zeta\amalg j_0\setminus j)\setminus\beta)\setminus j_0\amalg j} \big) \end{align} $$
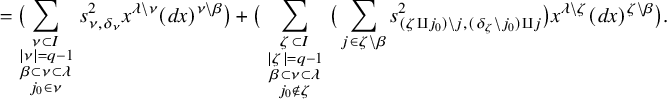 $$ \begin{align} &= \big(\!\!\!\!\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \\ j_0\in\nu \end{smallmatrix} } s^2_{\nu, \delta_\nu}x^{\lambda\setminus \nu}(dx)^{\nu\setminus\beta} \big) + \big(\sum_{ \begin{smallmatrix} \zeta\subset I \\ |\zeta|=q-1 \\ \beta\subset\nu\subset\lambda \\ j_0\notin\zeta \end{smallmatrix} } \big( \sum_{j\in \zeta\setminus\beta} s^2_{(\zeta\amalg j_0)\setminus j, (\delta_{\zeta}\setminus j_0)\amalg j}\big)x^{\lambda\setminus \zeta}(dx)^{\zeta\setminus\beta} \big). \end{align} $$
$$ \begin{align} &= \big(\!\!\!\!\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \\ \beta\subset\nu\subset\lambda \\ j_0\in\nu \end{smallmatrix} } s^2_{\nu, \delta_\nu}x^{\lambda\setminus \nu}(dx)^{\nu\setminus\beta} \big) + \big(\sum_{ \begin{smallmatrix} \zeta\subset I \\ |\zeta|=q-1 \\ \beta\subset\nu\subset\lambda \\ j_0\notin\zeta \end{smallmatrix} } \big( \sum_{j\in \zeta\setminus\beta} s^2_{(\zeta\amalg j_0)\setminus j, (\delta_{\zeta}\setminus j_0)\amalg j}\big)x^{\lambda\setminus \zeta}(dx)^{\zeta\setminus\beta} \big). \end{align} $$
Finally, by applying the relation (3.3) for
![]() $\xi =\zeta \amalg j_0$
and
$\xi =\zeta \amalg j_0$
and
![]() $\alpha =\delta _{\zeta }\setminus j_0$
, so that
$\alpha =\delta _{\zeta }\setminus j_0$
, so that
![]() $\xi \setminus \alpha =(\zeta \setminus \beta )\amalg j_0$
, we find that
$\xi \setminus \alpha =(\zeta \setminus \beta )\amalg j_0$
, we find that
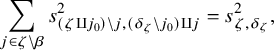 $$\begin{align*}\sum_{j\in \zeta\setminus\beta} s^2_{(\zeta\amalg j_0)\setminus j, (\delta_{\zeta}\setminus j_0)\amalg j}=s^2_{\zeta, \delta_\zeta}, \end{align*}$$
$$\begin{align*}\sum_{j\in \zeta\setminus\beta} s^2_{(\zeta\amalg j_0)\setminus j, (\delta_{\zeta}\setminus j_0)\amalg j}=s^2_{\zeta, \delta_\zeta}, \end{align*}$$
Let us remark that if
![]() $(x, y)$
is one of the generators of
$(x, y)$
is one of the generators of
![]() $J_{\langle 2^{n} \rangle }$
of Proposition 2.16, then x and y, when regarded as elements of
$J_{\langle 2^{n} \rangle }$
of Proposition 2.16, then x and y, when regarded as elements of
![]() $k\otimes _S k$
, belong to
$k\otimes _S k$
, belong to
![]() $J_{\langle 1 \rangle }$
. Thus, if an element
$J_{\langle 1 \rangle }$
. Thus, if an element
![]() $(z, w)$
of
$(z, w)$
of
![]() $\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
belongs to
$\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
belongs to
![]() $J_{\langle 2^{n} \rangle }^{q+1}$
for some
$J_{\langle 2^{n} \rangle }^{q+1}$
for some
![]() $q\geq 0$
, then z and w belong to
$q\geq 0$
, then z and w belong to
![]() $J_{\langle 1 \rangle }^{q+1}$
. The following lemma strengthens this property when the second component w is zero.
$J_{\langle 1 \rangle }^{q+1}$
. The following lemma strengthens this property when the second component w is zero.
Lemma 3.8. Let
![]() $z\in (k\otimes _S k)^{C_2}$
be such that
$z\in (k\otimes _S k)^{C_2}$
be such that
![]() $(z, 0)$
belongs to
$(z, 0)$
belongs to
![]() $J_{\langle 2^{n} \rangle }^{q+1}$
for some
$J_{\langle 2^{n} \rangle }^{q+1}$
for some
![]() $q\geq 0$
. Then z belongs to
$q\geq 0$
. Then z belongs to
![]() $J_{\langle 1 \rangle }^{q+2}$
.
$J_{\langle 1 \rangle }^{q+2}$
.
Proof. By the characterisation of
![]() $J_{\langle 2^{n} \rangle }$
of Proposition 2.16, we see that
$J_{\langle 2^{n} \rangle }$
of Proposition 2.16, we see that
![]() $(x, 0)$
can be expressed as a sum of elements
$(x, 0)$
can be expressed as a sum of elements
![]() $u_1\dots u_{q+1}$
, with
$u_1\dots u_{q+1}$
, with
![]() $u_j\in J_{\langle 2^{n} \rangle }$
, of three types:
$u_j\in J_{\langle 2^{n} \rangle }$
, of three types:
-
i) At least one of the
 $u_j$
is of the form
$u_j$
is of the form
 $V^{n-i}\tau _i(a\otimes b)+V^{n-i}\tau _i(ab\otimes 1)$
for
$V^{n-i}\tau _i(a\otimes b)+V^{n-i}\tau _i(ab\otimes 1)$
for
 $a, b\in k$
and
$a, b\in k$
and
 $0\leq i\leq n-1$
. We can then write this generator in components as where
$0\leq i\leq n-1$
. We can then write this generator in components as where $$\begin{align*}u_1\dots u_{q+1}=(w_1+w_1^{\prime}, 0)u_2\dots u_{q+1}, \end{align*}$$
$$\begin{align*}u_1\dots u_{q+1}=(w_1+w_1^{\prime}, 0)u_2\dots u_{q+1}, \end{align*}$$
 $w_1$
is the first component of
$w_1$
is the first component of
 $V^{n-i}\tau _i(a\otimes b)$
and
$V^{n-i}\tau _i(a\otimes b)$
and
 $w_1^{\prime }$
the first component of
$w_1^{\prime }$
the first component of
 $V^{n-i}\tau _i(ab\otimes 1)$
.
$V^{n-i}\tau _i(ab\otimes 1)$
.
-
ii) All of the
 $u_j$
are of the form
$u_j$
are of the form
 $V^{n-i}\tau _i(a\otimes b)+\sigma V^{n-i}\tau _i(a\otimes b)$
for
$V^{n-i}\tau _i(a\otimes b)+\sigma V^{n-i}\tau _i(a\otimes b)$
for
 $a, b\in k$
and
$a, b\in k$
and
 $0\leq i\leq n-1$
. Then each factor is diagonal; that is,
$0\leq i\leq n-1$
. Then each factor is diagonal; that is,
 $u_j=(v_j, v_j)$
where
$u_j=(v_j, v_j)$
where
 $v_j$
is in
$v_j$
is in
 $J_{\langle 1\rangle }$
, and
$J_{\langle 1\rangle }$
, and  $$\begin{align*}u_1\dots u_{q+1}=(v_1\dots v_{q+1}, v_1\dots v_{q+1}). \end{align*}$$
$$\begin{align*}u_1\dots u_{q+1}=(v_1\dots v_{q+1}, v_1\dots v_{q+1}). \end{align*}$$
-
iii) It is not of the first two types. In this case, at least one of the
 $u_j$
is of the form
$u_j$
is of the form
 $\tau _n(a\otimes b)+\tau _n(ab\otimes 1)$
and the other factors are diagonal. We can then write such a generator as for some
$\tau _n(a\otimes b)+\tau _n(ab\otimes 1)$
and the other factors are diagonal. We can then write such a generator as for some $$ \begin{align*} u_1\dots u_{q+1}&=(t_1, t_1^{\prime})\dots (t_l, t_l^{\prime})(s_{l+1}, s_{l+1})\dots (s_{q+1}, s_{q+1}) \\&=(t_1\dots t_ls_{l+1}\dots s_{q+1}, t_1^{\prime}\dots t_l^{\prime}s_{l+1}\dots s_{q+1}) \end{align*} $$
$$ \begin{align*} u_1\dots u_{q+1}&=(t_1, t_1^{\prime})\dots (t_l, t_l^{\prime})(s_{l+1}, s_{l+1})\dots (s_{q+1}, s_{q+1}) \\&=(t_1\dots t_ls_{l+1}\dots s_{q+1}, t_1^{\prime}\dots t_l^{\prime}s_{l+1}\dots s_{q+1}) \end{align*} $$
 $1\leq l\leq q+1$
, where
$1\leq l\leq q+1$
, where
 $t_j=\phi _n(a_j\otimes b_j)+\phi _n(a_jb_j\otimes 1)$
,
$t_j=\phi _n(a_j\otimes b_j)+\phi _n(a_jb_j\otimes 1)$
,
 $t_j^{\prime }=\phi _n(b_j\otimes a_j)+\phi _n(1\otimes a_jb_j)$
, and
$t_j^{\prime }=\phi _n(b_j\otimes a_j)+\phi _n(1\otimes a_jb_j)$
, and
 $s_j$
is in
$s_j$
is in
 $J_{\langle 1\rangle }$
.
$J_{\langle 1\rangle }$
.
Thus, let us write
![]() $(z, 0)$
as a sum of these types of generators, where we omit the indexing from the sums to make this expression more digestible:
$(z, 0)$
as a sum of these types of generators, where we omit the indexing from the sums to make this expression more digestible:
 $$\begin{align*}(z, 0)&=\sum (w_1+w_1^{\prime}, 0)u_2\dots u_{q+1} +\sum(v_1\dots v_{q+1}, v_1\dots v_{q+1}) \\&\quad+\sum (t_1\dots t_ls_{l+1}\dots s_{q+1}, t_1^{\prime}\dots t_l^{\prime}s_{l+1}\dots s_{q+1}). \end{align*}$$
$$\begin{align*}(z, 0)&=\sum (w_1+w_1^{\prime}, 0)u_2\dots u_{q+1} +\sum(v_1\dots v_{q+1}, v_1\dots v_{q+1}) \\&\quad+\sum (t_1\dots t_ls_{l+1}\dots s_{q+1}, t_1^{\prime}\dots t_l^{\prime}s_{l+1}\dots s_{q+1}). \end{align*}$$
Since the second component of
![]() $(z, 0)$
is null, we must have that
$(z, 0)$
is null, we must have that
By replacing the left-hand side in the first component above, we have that z is, by denoting
![]() $r_j$
the first component of
$r_j$
the first component of
![]() $u_j$
, of the form
$u_j$
, of the form
 $$ \begin{align*} z&=\sum (w_1+w_1^{\prime})r_2\dots r_{q+1}+\sum t_1^{\prime}\dots t_l^{\prime}s_{l+1}\dots s_{q+1}+\sum t_1\dots t_ls_{l+1}\dots s_{q+1} \\&=\sum(w_1+w_1^{\prime})r_2\dots r_{q+1}+\sum (t_1\dots t_l+t_1^{\prime}\dots t_l^{\prime})s_{l+1}\dots s_{q+1}. \end{align*} $$
$$ \begin{align*} z&=\sum (w_1+w_1^{\prime})r_2\dots r_{q+1}+\sum t_1^{\prime}\dots t_l^{\prime}s_{l+1}\dots s_{q+1}+\sum t_1\dots t_ls_{l+1}\dots s_{q+1} \\&=\sum(w_1+w_1^{\prime})r_2\dots r_{q+1}+\sum (t_1\dots t_l+t_1^{\prime}\dots t_l^{\prime})s_{l+1}\dots s_{q+1}. \end{align*} $$
Thus, since the
![]() $r_j$
and
$r_j$
and
![]() $s_j$
belong to
$s_j$
belong to
![]() $J_{\langle 1 \rangle }$
, to conclude the proof, it is sufficient to show that
$J_{\langle 1 \rangle }$
, to conclude the proof, it is sufficient to show that
![]() $w_1+w_1^{\prime }$
belongs to
$w_1+w_1^{\prime }$
belongs to
![]() $J_{\langle 1 \rangle }^2$
and that
$J_{\langle 1 \rangle }^2$
and that
![]() $(t_1\dots t_l+t_1^{\prime }\dots t_l^{\prime })$
belongs to
$(t_1\dots t_l+t_1^{\prime }\dots t_l^{\prime })$
belongs to
![]() $J_{\langle 1 \rangle }^{l+1}$
. For the first case, we have that
$J_{\langle 1 \rangle }^{l+1}$
. For the first case, we have that
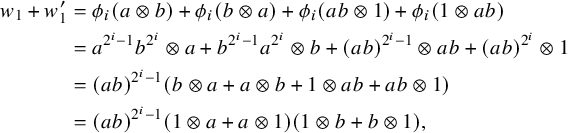 $$ \begin{align*} w_1+w_1^{\prime}&=\phi_i(a\otimes b)+\phi_i(b\otimes a)+\phi_i(ab\otimes 1)+\phi_i(1\otimes ab) \\&= a^{2^i-1}b^{2^i}\otimes a+b^{2^i-1}a^{2^i}\otimes b+(ab)^{2^i-1}\otimes ab+(ab)^{2^i}\otimes 1 \\&=(ab)^{2^i-1}(b\otimes a+a\otimes b+1\otimes ab+ab\otimes 1) \\&=(ab)^{2^i-1}(1\otimes a+a\otimes 1)(1\otimes b+b\otimes 1), \end{align*} $$
$$ \begin{align*} w_1+w_1^{\prime}&=\phi_i(a\otimes b)+\phi_i(b\otimes a)+\phi_i(ab\otimes 1)+\phi_i(1\otimes ab) \\&= a^{2^i-1}b^{2^i}\otimes a+b^{2^i-1}a^{2^i}\otimes b+(ab)^{2^i-1}\otimes ab+(ab)^{2^i}\otimes 1 \\&=(ab)^{2^i-1}(b\otimes a+a\otimes b+1\otimes ab+ab\otimes 1) \\&=(ab)^{2^i-1}(1\otimes a+a\otimes 1)(1\otimes b+b\otimes 1), \end{align*} $$
which indeed belongs to
![]() $J_{\langle 1 \rangle }^2$
. For the second case, we have that
$J_{\langle 1 \rangle }^2$
. For the second case, we have that
![]() $(t_1\dots t_l+t_1^{\prime }\dots t_l^{\prime })$
is equal to
$(t_1\dots t_l+t_1^{\prime }\dots t_l^{\prime })$
is equal to
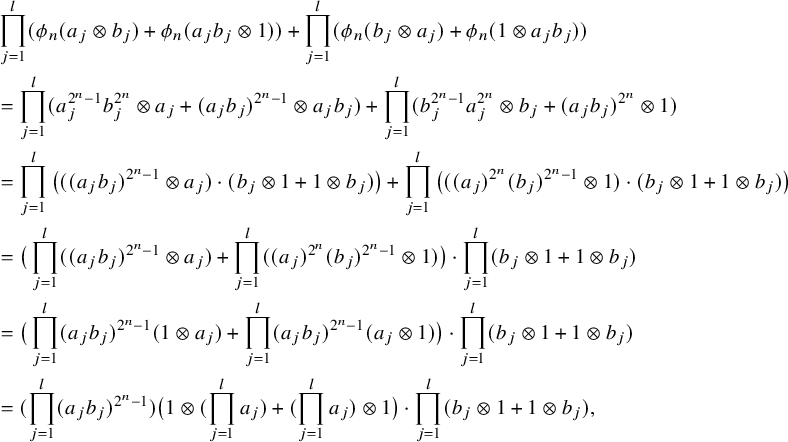 $$ \begin{align*} &\prod_{j=1}^l(\phi_n(a_j\otimes b_j)+\phi_n(a_jb_j\otimes 1))+\prod_{j=1}^l(\phi_n(b_j\otimes a_j)+\phi_n(1\otimes a_jb_j)) \\&=\prod_{j=1}^l(a_j^{2^n-1}b_j^{2^n}\otimes a_j+(a_jb_j)^{2^n-1}\otimes a_jb_j)+\prod_{j=1}^l(b_j^{2^n-1}a_j^{2^n}\otimes b_j+(a_jb_j)^{2^n}\otimes 1) \\& =\prod_{j=1}^l\big(((a_jb_j)^{2^n-1}\otimes a_j)\cdot (b_j\otimes 1+1\otimes b_j)\big) + \prod_{j=1}^l\big( ((a_j)^{2^n}(b_j)^{2^n-1}\otimes 1) \cdot (b_j\otimes 1+1\otimes b_j) \big) \\ &= \big(\prod_{j=1}^l((a_jb_j)^{2^n-1}\otimes a_j)+\prod_{j=1}^l((a_j)^{2^n}(b_j)^{2^n-1}\otimes 1)\big) \cdot \prod_{j=1}^l (b_j\otimes 1+1\otimes b_j) \\&= \big(\prod_{j=1}^l(a_jb_j)^{2^n-1}(1 \otimes a_j)+\prod_{j=1}^l(a_jb_j)^{2^n-1}(a_j\otimes 1)\big) \cdot \prod_{j=1}^l (b_j\otimes 1+1\otimes b_j) \\&= (\prod_{j=1}^l(a_jb_j)^{2^n-1})\big(1 \otimes (\prod_{j=1}^la_j)+(\prod_{j=1}^la_j)\otimes 1\big) \cdot \prod_{j=1}^l (b_j\otimes 1+1\otimes b_j), \end{align*} $$
$$ \begin{align*} &\prod_{j=1}^l(\phi_n(a_j\otimes b_j)+\phi_n(a_jb_j\otimes 1))+\prod_{j=1}^l(\phi_n(b_j\otimes a_j)+\phi_n(1\otimes a_jb_j)) \\&=\prod_{j=1}^l(a_j^{2^n-1}b_j^{2^n}\otimes a_j+(a_jb_j)^{2^n-1}\otimes a_jb_j)+\prod_{j=1}^l(b_j^{2^n-1}a_j^{2^n}\otimes b_j+(a_jb_j)^{2^n}\otimes 1) \\& =\prod_{j=1}^l\big(((a_jb_j)^{2^n-1}\otimes a_j)\cdot (b_j\otimes 1+1\otimes b_j)\big) + \prod_{j=1}^l\big( ((a_j)^{2^n}(b_j)^{2^n-1}\otimes 1) \cdot (b_j\otimes 1+1\otimes b_j) \big) \\ &= \big(\prod_{j=1}^l((a_jb_j)^{2^n-1}\otimes a_j)+\prod_{j=1}^l((a_j)^{2^n}(b_j)^{2^n-1}\otimes 1)\big) \cdot \prod_{j=1}^l (b_j\otimes 1+1\otimes b_j) \\&= \big(\prod_{j=1}^l(a_jb_j)^{2^n-1}(1 \otimes a_j)+\prod_{j=1}^l(a_jb_j)^{2^n-1}(a_j\otimes 1)\big) \cdot \prod_{j=1}^l (b_j\otimes 1+1\otimes b_j) \\&= (\prod_{j=1}^l(a_jb_j)^{2^n-1})\big(1 \otimes (\prod_{j=1}^la_j)+(\prod_{j=1}^la_j)\otimes 1\big) \cdot \prod_{j=1}^l (b_j\otimes 1+1\otimes b_j), \end{align*} $$
which belongs to
![]() $J_{\langle 1 \rangle }^{l+1}$
.
$J_{\langle 1 \rangle }^{l+1}$
.
Proof of Theorem 3.4
By Remark 3.5, in degree
![]() $q=0$
, the map
$q=0$
, the map
![]() $u_n$
is an isomorphism for all
$u_n$
is an isomorphism for all
![]() $n\geq 0$
. Thus, let
$n\geq 0$
. Thus, let
![]() $q\geq 1$
. By Lemma 3.6, the map
$q\geq 1$
. By Lemma 3.6, the map
![]() $u_0\colon \Omega ^q_k\longrightarrow J_{\langle 1\rangle }^q/J_{\langle 1\rangle }^{q+1}$
is an isomorphism for every
$u_0\colon \Omega ^q_k\longrightarrow J_{\langle 1\rangle }^q/J_{\langle 1\rangle }^{q+1}$
is an isomorphism for every
![]() $q\geq 1$
. Thus, let
$q\geq 1$
. Thus, let
![]() $n\geq 1$
, assume that
$n\geq 1$
, assume that
![]() $u_{n-1}$
is an isomorphism, and let us show that
$u_{n-1}$
is an isomorphism, and let us show that
![]() $u_{n}$
is an isomorphism. Since
$u_{n}$
is an isomorphism. Since
![]() $u_{n}$
is a map of Witt complexes, it clearly hits all the generators of
$u_{n}$
is a map of Witt complexes, it clearly hits all the generators of
![]() $J_{\langle 2^{n} \rangle }^q$
from Proposition 2.16, and it is therefore surjective. To see that it is injective, consider the commutative diagram with exact rows
$J_{\langle 2^{n} \rangle }^q$
from Proposition 2.16, and it is therefore surjective. To see that it is injective, consider the commutative diagram with exact rows

where the top row is exact by [Reference CosteanuCos08, Lemma 3.5]. It then suffices to show that
![]() $u_{n}$
is injective when restricted to the image of the top left horizontal map
$u_{n}$
is injective when restricted to the image of the top left horizontal map
![]() $V^n+dV^n$
. Thus, let
$V^n+dV^n$
. Thus, let
![]() $a\in \Omega ^q_k$
and
$a\in \Omega ^q_k$
and
![]() $b\in \Omega ^{q-1}_k$
, and suppose that
$b\in \Omega ^{q-1}_k$
, and suppose that
![]() $u_{n}(V^n(a)+dV^n(b))$
can be represented by an element of
$u_{n}(V^n(a)+dV^n(b))$
can be represented by an element of
![]() $J_{\langle 2^{n} \rangle }^{q+1}$
. We need to show that
$J_{\langle 2^{n} \rangle }^{q+1}$
. We need to show that
![]() $c:=V^n(a)+dV^n(b)$
is divisible by
$c:=V^n(a)+dV^n(b)$
is divisible by
![]() $2$
in
$2$
in
![]() ${\mathrm {W}}_{\langle 2^{n}\rangle }\Omega ^q_k$
. Let us explicitly calculate
${\mathrm {W}}_{\langle 2^{n}\rangle }\Omega ^q_k$
. Let us explicitly calculate
![]() $u_{n}(V^n(a)+dV^n(b))$
. Given a
$u_{n}(V^n(a)+dV^n(b))$
. Given a
![]() $2$
-basis
$2$
-basis
![]() $\{x_{i}\}_{i\in I}$
of k, let us write
$\{x_{i}\}_{i\in I}$
of k, let us write
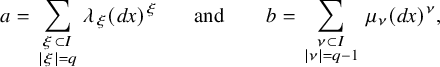 $$\begin{align*}a=\sum_{ \begin{smallmatrix} \xi\subset I \\ |\xi|=q \end{smallmatrix} }\lambda_\xi(dx)^\xi \ \ \ \ \ \ \ \mbox{and}\ \ \ \ \ \ \ \ b=\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} }\mu_\nu(dx)^\nu, \end{align*}$$
$$\begin{align*}a=\sum_{ \begin{smallmatrix} \xi\subset I \\ |\xi|=q \end{smallmatrix} }\lambda_\xi(dx)^\xi \ \ \ \ \ \ \ \mbox{and}\ \ \ \ \ \ \ \ b=\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} }\mu_\nu(dx)^\nu, \end{align*}$$
where
![]() $\lambda _\xi , \mu _\nu \in k$
and
$\lambda _\xi , \mu _\nu \in k$
and
![]() $(dx)^\xi =\prod _{i\in \xi }dx_i$
. Since u is a map of Witt complexes, we must have that
$(dx)^\xi =\prod _{i\in \xi }dx_i$
. Since u is a map of Witt complexes, we must have that
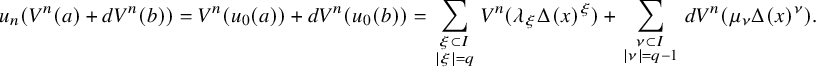 $$\begin{align*}u_{n}(V^n(a)+dV^n(b))=V^n(u_0(a))+dV^n(u_0(b))= \sum_{ \begin{smallmatrix} \xi\subset I \\ |\xi|=q \end{smallmatrix} }V^n(\lambda_\xi\Delta(x)^\xi) + \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } dV^n(\mu_\nu \Delta(x)^\nu). \end{align*}$$
$$\begin{align*}u_{n}(V^n(a)+dV^n(b))=V^n(u_0(a))+dV^n(u_0(b))= \sum_{ \begin{smallmatrix} \xi\subset I \\ |\xi|=q \end{smallmatrix} }V^n(\lambda_\xi\Delta(x)^\xi) + \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } dV^n(\mu_\nu \Delta(x)^\nu). \end{align*}$$
Recall from Proposition 2.10 that for every
![]() $x\otimes y\in k\otimes _S k$
, we have that
$x\otimes y\in k\otimes _S k$
, we have that
![]() $V^n(x\otimes y)$
is represented by
$V^n(x\otimes y)$
is represented by
![]() $({\mathrm {tran}}(x\otimes y), 0)$
in
$({\mathrm {tran}}(x\otimes y), 0)$
in
![]() $\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
, where
$\pi _0\ {\mathrm {TRR}}^{n+1}(k;2)^{\phi \mathbb {Z}/2}$
, where
![]() ${\mathrm {tran}}(x\otimes y)=x\otimes y+y\otimes x$
. Thus, since
${\mathrm {tran}}(x\otimes y)=x\otimes y+y\otimes x$
. Thus, since
![]() $d=1+\sigma $
, we have
$d=1+\sigma $
, we have
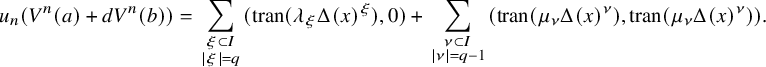 $$ \begin{align*} u_{n}(V^n(a)+dV^n(b))&= \sum_{ \begin{smallmatrix} \xi\subset I \\ |\xi|=q \end{smallmatrix} }({\mathrm{tran}}(\lambda_\xi\Delta(x)^\xi), 0) + \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } ({\mathrm{tran}}(\mu_\nu \Delta(x)^\nu), {\mathrm{tran}}(\mu_\nu \Delta(x)^\nu)). \end{align*} $$
$$ \begin{align*} u_{n}(V^n(a)+dV^n(b))&= \sum_{ \begin{smallmatrix} \xi\subset I \\ |\xi|=q \end{smallmatrix} }({\mathrm{tran}}(\lambda_\xi\Delta(x)^\xi), 0) + \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } ({\mathrm{tran}}(\mu_\nu \Delta(x)^\nu), {\mathrm{tran}}(\mu_\nu \Delta(x)^\nu)). \end{align*} $$
By choosing
![]() $i\in \xi $
, we can write
$i\in \xi $
, we can write
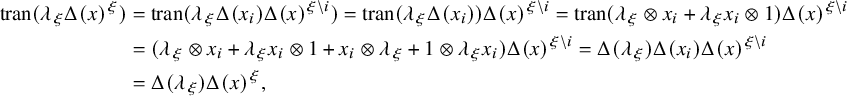 $$ \begin{align*} {\mathrm{tran}}(\lambda_\xi\Delta(x)^\xi)&={\mathrm{tran}}(\lambda_\xi\Delta(x_i)\Delta(x)^{\xi\setminus i})={\mathrm{tran}}(\lambda_\xi\Delta(x_i))\Delta(x)^{\xi\setminus i}={\mathrm{tran}}(\lambda_\xi\otimes x_i+\lambda_\xi x_i\otimes 1)\Delta(x)^{\xi\setminus i} \\&= (\lambda_\xi\otimes x_i+\lambda_\xi x_i\otimes 1+x_i\otimes \lambda_\xi+1\otimes \lambda_\xi x_i)\Delta(x)^{\xi\setminus i}=\Delta(\lambda_\xi)\Delta(x_i)\Delta(x)^{\xi\setminus i} \\&=\Delta(\lambda_\xi)\Delta(x)^{\xi}, \end{align*} $$
$$ \begin{align*} {\mathrm{tran}}(\lambda_\xi\Delta(x)^\xi)&={\mathrm{tran}}(\lambda_\xi\Delta(x_i)\Delta(x)^{\xi\setminus i})={\mathrm{tran}}(\lambda_\xi\Delta(x_i))\Delta(x)^{\xi\setminus i}={\mathrm{tran}}(\lambda_\xi\otimes x_i+\lambda_\xi x_i\otimes 1)\Delta(x)^{\xi\setminus i} \\&= (\lambda_\xi\otimes x_i+\lambda_\xi x_i\otimes 1+x_i\otimes \lambda_\xi+1\otimes \lambda_\xi x_i)\Delta(x)^{\xi\setminus i}=\Delta(\lambda_\xi)\Delta(x_i)\Delta(x)^{\xi\setminus i} \\&=\Delta(\lambda_\xi)\Delta(x)^{\xi}, \end{align*} $$
where the second equality holds since
![]() $\Delta (x)^{\xi \setminus i}$
is fixed by the involution. Similarly,
$\Delta (x)^{\xi \setminus i}$
is fixed by the involution. Similarly,
![]() ${\mathrm {tran}}(\mu _\nu \Delta (x)^\nu )=\Delta (\mu _\nu )\Delta (x)^{\nu }$
(which is obvious in the case where
${\mathrm {tran}}(\mu _\nu \Delta (x)^\nu )=\Delta (\mu _\nu )\Delta (x)^{\nu }$
(which is obvious in the case where
![]() $q=1$
and
$q=1$
and
![]() $\nu =\emptyset $
). Thus, we find that
$\nu =\emptyset $
). Thus, we find that
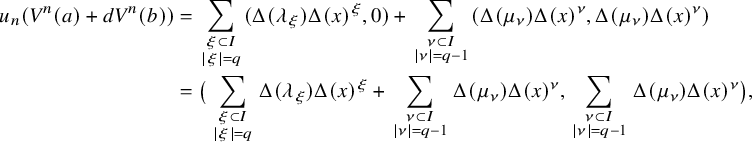 $$ \begin{align*} u_{n}(V^n(a)+dV^n(b))&= \sum_{ \begin{smallmatrix} \xi\subset I \\ |\xi|=q \end{smallmatrix} }(\Delta(\lambda_\xi)\Delta(x)^{\xi}, 0) + \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } (\Delta(\mu_\nu)\Delta(x)^{\nu}, \Delta(\mu_\nu)\Delta(x)^{\nu}) \\&= \big( \sum_{ \begin{smallmatrix} \xi\subset I \\ |\xi|=q \end{smallmatrix} }\Delta(\lambda_\xi)\Delta(x)^{\xi} + \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} }\Delta(\mu_\nu)\Delta(x)^{\nu} , \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} }\Delta(\mu_\nu)\Delta(x)^{\nu} \big), \end{align*} $$
$$ \begin{align*} u_{n}(V^n(a)+dV^n(b))&= \sum_{ \begin{smallmatrix} \xi\subset I \\ |\xi|=q \end{smallmatrix} }(\Delta(\lambda_\xi)\Delta(x)^{\xi}, 0) + \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} } (\Delta(\mu_\nu)\Delta(x)^{\nu}, \Delta(\mu_\nu)\Delta(x)^{\nu}) \\&= \big( \sum_{ \begin{smallmatrix} \xi\subset I \\ |\xi|=q \end{smallmatrix} }\Delta(\lambda_\xi)\Delta(x)^{\xi} + \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} }\Delta(\mu_\nu)\Delta(x)^{\nu} , \sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} }\Delta(\mu_\nu)\Delta(x)^{\nu} \big), \end{align*} $$
and this element is by assumption in
![]() $J_{\langle 2^{n} \rangle }^{q+1}$
. Let us analyse the two components separately, starting from the second one. As observed above Lemma 3.8, these components must in fact belong to
$J_{\langle 2^{n} \rangle }^{q+1}$
. Let us analyse the two components separately, starting from the second one. As observed above Lemma 3.8, these components must in fact belong to
![]() $J_{\langle 1 \rangle }^{q+1}$
, and therefore,
$J_{\langle 1 \rangle }^{q+1}$
, and therefore,
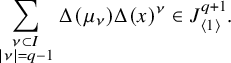 $$\begin{align*}\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} }\Delta(\mu_\nu)\Delta(x)^{\nu} \in J_{\langle 1 \rangle}^{q+1}. \end{align*}$$
$$\begin{align*}\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} }\Delta(\mu_\nu)\Delta(x)^{\nu} \in J_{\langle 1 \rangle}^{q+1}. \end{align*}$$
By Lemma 3.7,
![]() $V(\mu _\nu (dx)^\nu )$
vanishes in the de Rham Witt complex modulo
$V(\mu _\nu (dx)^\nu )$
vanishes in the de Rham Witt complex modulo
![]() $2$
, and therefore so does
$2$
, and therefore so does
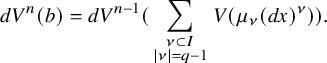 $$\begin{align*}dV^n(b)=dV^{n-1}(\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} }V(\mu_\nu (dx)^\nu)). \end{align*}$$
$$\begin{align*}dV^n(b)=dV^{n-1}(\sum_{ \begin{smallmatrix} \nu\subset I \\ |\nu|=q-1 \end{smallmatrix} }V(\mu_\nu (dx)^\nu)). \end{align*}$$
Our original element
![]() $c=V^n(a)+dV^n(b)$
is then equal to
$c=V^n(a)+dV^n(b)$
is then equal to
![]() $V^n(a)$
in the de Rham-Witt complex modulo
$V^n(a)$
in the de Rham-Witt complex modulo
![]() $2$
, and the map
$2$
, and the map
![]() $u_n$
sends this element to
$u_n$
sends this element to
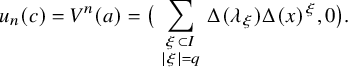 $$\begin{align*}u_n(c)=V^n(a)=\big( \sum_{ \begin{smallmatrix} \xi\subset I \\ |\xi|=q \end{smallmatrix} }\Delta(\lambda_\xi)\Delta(x)^{\xi} , 0 \big). \end{align*}$$
$$\begin{align*}u_n(c)=V^n(a)=\big( \sum_{ \begin{smallmatrix} \xi\subset I \\ |\xi|=q \end{smallmatrix} }\Delta(\lambda_\xi)\Delta(x)^{\xi} , 0 \big). \end{align*}$$
Moreover, this element is by assumption in
![]() $J_{\langle 2^{n} \rangle }^{q+1}$
. By applying Lemma 3.8, the first component
$J_{\langle 2^{n} \rangle }^{q+1}$
. By applying Lemma 3.8, the first component
![]() $\sum _{ \begin {smallmatrix} \xi \subset I \\ |\xi |=q \end {smallmatrix} }\Delta (\lambda _\xi )\Delta (x)^{\xi }$
in fact belongs to
$\sum _{ \begin {smallmatrix} \xi \subset I \\ |\xi |=q \end {smallmatrix} }\Delta (\lambda _\xi )\Delta (x)^{\xi }$
in fact belongs to
![]() $J_{\langle 1 \rangle }^{q+2}$
. Again by Lemma 3.7, we find that
$J_{\langle 1 \rangle }^{q+2}$
. Again by Lemma 3.7, we find that
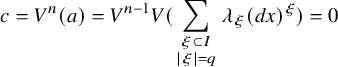 $$\begin{align*}c=V^n(a)=V^{n-1}V(\sum_{ \begin{smallmatrix} \xi\subset I \\ |\xi|=q \end{smallmatrix} }\lambda_\xi(dx)^{\xi})=0\end{align*}$$
$$\begin{align*}c=V^n(a)=V^{n-1}V(\sum_{ \begin{smallmatrix} \xi\subset I \\ |\xi|=q \end{smallmatrix} }\lambda_\xi(dx)^{\xi})=0\end{align*}$$
in
![]() $({\mathrm {W}}_{\langle 2^{n}\rangle }\Omega ^q_k)/2$
, proving that
$({\mathrm {W}}_{\langle 2^{n}\rangle }\Omega ^q_k)/2$
, proving that
![]() $u_n$
is injective.
$u_n$
is injective.
3.3 The Milnor conjecture and TCR
Let us recall that the
![]() $2$
-typical topological cyclic homology spectrum
$2$
-typical topological cyclic homology spectrum
![]() ${\mathrm {TC}}(k;2)$
of k can be defined as the equaliser
${\mathrm {TC}}(k;2)$
of k can be defined as the equaliser
of the identity and the Frobenius map of
![]() ${\mathrm {TR}}(k;2)$
. Let us denote
${\mathrm {TR}}(k;2)$
. Let us denote
![]() ${\mathrm {W}}_{\langle 2^{\infty }\rangle }\Omega ^\ast _k$
the limit of
${\mathrm {W}}_{\langle 2^{\infty }\rangle }\Omega ^\ast _k$
the limit of
![]() ${\mathrm {W}}_{\langle 2^{n}\rangle }\Omega ^\ast _k$
over the map R, and define
${\mathrm {W}}_{\langle 2^{n}\rangle }\Omega ^\ast _k$
over the map R, and define
![]() $\nu _\ast ^{dRW/2}(k;2)$
and
$\nu _\ast ^{dRW/2}(k;2)$
and
![]() $\epsilon _\ast ^{dRW/2}(k;2)$
respectively as the equaliser and coequaliser of the parallel group homomorphisms
$\epsilon _\ast ^{dRW/2}(k;2)$
respectively as the equaliser and coequaliser of the parallel group homomorphisms
Then, since the parallel arrows are ring homomorphisms,
![]() $\nu ^\ast _{dRW/2}(k;2)$
is a graded ring, and
$\nu ^\ast _{dRW/2}(k;2)$
is a graded ring, and
![]() $\epsilon ^\ast _{dRW/2}(k;2)$
is a graded
$\epsilon ^\ast _{dRW/2}(k;2)$
is a graded
![]() $\nu ^\ast _{dRW/2}(k;2)$
-module (where the action on the latter is defined via either of the maps
$\nu ^\ast _{dRW/2}(k;2)$
-module (where the action on the latter is defined via either of the maps
![]() ${\mathrm {id}}$
or F). We now prove a version of the Milnor conjecture for
${\mathrm {id}}$
or F). We now prove a version of the Milnor conjecture for
![]() $\nu ^\ast _{dRW/2}(k;2)$
and
$\nu ^\ast _{dRW/2}(k;2)$
and
![]() $\epsilon ^\ast _{dRW/2}(k;2)$
, which describes these in terms of the graded ring associated to the kernel of the restriction map
$\epsilon ^\ast _{dRW/2}(k;2)$
, which describes these in terms of the graded ring associated to the kernel of the restriction map
where the involution on
![]() $\pi _0{\mathrm {TC}}(k;2)$
is induced by the involution underlying the
$\pi _0{\mathrm {TC}}(k;2)$
is induced by the involution underlying the
![]() $\mathbb {Z}/2$
-spectrum
$\mathbb {Z}/2$
-spectrum
![]() ${\mathrm {TCR}}(k;2)$
. The restriction map is defined as we did at the beginning of §2.3. Let us also define the
${\mathrm {TCR}}(k;2)$
. The restriction map is defined as we did at the beginning of §2.3. Let us also define the
![]() $\pi _{0}{\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
-module
$\pi _{0}{\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
-module
so that the quotients
![]() $K^{\ast }T_{-1}/K^{\ast +1}T_{-1}$
form a graded
$K^{\ast }T_{-1}/K^{\ast +1}T_{-1}$
form a graded
![]() $K^{\ast }/K^{\ast +1}$
-module.
$K^{\ast }/K^{\ast +1}$
-module.
Theorem 3.9. Let k be a field of characteristic
![]() $2$
. There is an isomorphism of graded rings
$2$
. There is an isomorphism of graded rings
and an isomorphism of graded
![]() $K^\ast /K^{\ast +1}$
-modules
$K^\ast /K^{\ast +1}$
-modules
Proof. Let
![]() $\nu ^\ast (k)$
and be
$\nu ^\ast (k)$
and be
![]() $\epsilon ^\ast (k)$
be respectively the equaliser and coequaliser of the projection map and the inverse Cartier operator
$\epsilon ^\ast (k)$
be respectively the equaliser and coequaliser of the projection map and the inverse Cartier operator
The map R of the de Rham-Witt complex induces multiplicative maps
![]() $\nu _{dRW/2}^\ast (k;2)\to \nu ^\ast (k)$
and
$\nu _{dRW/2}^\ast (k;2)\to \nu ^\ast (k)$
and
![]() $\epsilon _{dRW/2}^\ast (k;2)\to \epsilon ^\ast (k)$
, which are isomorphisms by the proof of [Reference Clausen, Mathew and MorrowCMM21, Proposition 2.26]. Moreover, by [Reference KatoKat82, Theorem (2)], the graded ring associated to the fundamental ideal I of the symmetric Witt group is isomorphic to
$\epsilon _{dRW/2}^\ast (k;2)\to \epsilon ^\ast (k)$
, which are isomorphisms by the proof of [Reference Clausen, Mathew and MorrowCMM21, Proposition 2.26]. Moreover, by [Reference KatoKat82, Theorem (2)], the graded ring associated to the fundamental ideal I of the symmetric Witt group is isomorphic to
![]() $\nu ^\ast (k)$
, and the graded module
$\nu ^\ast (k)$
, and the graded module
![]() $I^\ast {\mathrm {W}}^q(k)/I^{\ast +1} {\mathrm {W}}^q(k)$
to
$I^\ast {\mathrm {W}}^q(k)/I^{\ast +1} {\mathrm {W}}^q(k)$
to
![]() $\epsilon ^\ast (k)$
. Thus, since [Reference KatoKat82, Theorem (1)] and Corollary 2.5 identify
$\epsilon ^\ast (k)$
. Thus, since [Reference KatoKat82, Theorem (1)] and Corollary 2.5 identify
![]() ${\mathrm {W}}^s(k)$
and
${\mathrm {W}}^s(k)$
and
![]() $\pi _0{\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
, as rings, with the equaliser of
$\pi _0{\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
, as rings, with the equaliser of
and
![]() ${\mathrm {W}}^q(k)$
and
${\mathrm {W}}^q(k)$
and
![]() $T_{-1}$
, as modules, with their coequaliser, it suffices to show that I and K correspond to the same ideal under these identifications.
$T_{-1}$
, as modules, with their coequaliser, it suffices to show that I and K correspond to the same ideal under these identifications.
For the symmetric Witt group, the isomorphism with the equaliser is given by the unique additive map that sends the rank
![]() $1$
form
$1$
form
![]() $\langle a\rangle $
, with
$\langle a\rangle $
, with
![]() $a\in k^\times $
, to
$a\in k^\times $
, to
![]() $a^{-1}\otimes a$
. For
$a^{-1}\otimes a$
. For
![]() $\pi _0{\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
, it is induced by the map
$\pi _0{\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
, it is induced by the map
followed by the identification of the target with
![]() $(k\otimes _S k)^{C_2}$
from Proposition 2.3. Let us note that, after including the fixed points into
$(k\otimes _S k)^{C_2}$
from Proposition 2.3. Let us note that, after including the fixed points into
![]() $k\otimes _Sk$
, this is the map
$k\otimes _Sk$
, this is the map
where the isomorphism is from [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 5.1] (there it is stated for the fixed points, but since the transfer map of k is zero, the isomorphism descends to the geometric fixed points). Thus, in order to compare I and K, it suffices to show that, under the isomorphism of Corollary 2.5, the restriction map from
![]() $\pi _0{\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
to
$\pi _0{\mathrm {TCR}}(k;2)^{\phi \mathbb {Z}/2}$
to
![]() $(\pi _0{\mathrm {TC}}(k;2))^{\mathbb {Z}/2}/Im(1+w)$
sends
$(\pi _0{\mathrm {TC}}(k;2))^{\mathbb {Z}/2}/Im(1+w)$
sends
![]() $a^{-1}\otimes a$
to
$a^{-1}\otimes a$
to
![]() $1$
. As we do not have a good handle of
$1$
. As we do not have a good handle of
![]() $\pi _0{\mathrm {TC}}(k;2)$
for a general field k, we found ourselves unable to prove this by direct calculation.
$\pi _0{\mathrm {TC}}(k;2)$
for a general field k, we found ourselves unable to prove this by direct calculation.
Instead, we can employ the existence of a trace map of
![]() $\mathbb {Z}/2$
-equivariant spectra
$\mathbb {Z}/2$
-equivariant spectra
![]() ${\mathrm {tr}}\colon {\mathrm {KR}}(k)\to {\mathrm {TCR}}(k;2)$
which lifts the trace map
${\mathrm {tr}}\colon {\mathrm {KR}}(k)\to {\mathrm {TCR}}(k;2)$
which lifts the trace map
![]() ${\mathrm {K}}(k)\to {\mathrm {TC}}(k;2)$
from [Reference Bökstedt, Hsiang and MadsenBHM93]. This trace map is constructed in the forthcoming paper [Reference Harpaz, Nikolaus and ShahHNS21] in the setting of Poincaré
${\mathrm {K}}(k)\to {\mathrm {TC}}(k;2)$
from [Reference Bökstedt, Hsiang and MadsenBHM93]. This trace map is constructed in the forthcoming paper [Reference Harpaz, Nikolaus and ShahHNS21] in the setting of Poincaré
![]() $\infty $
-categories. For the purpose of our paper, we content ourselves with giving a point-set construction of this trace map in the case of rings with involution, as carried out in Proposition A.1 below. In fact, we need very little from this trace map: since
$\infty $
-categories. For the purpose of our paper, we content ourselves with giving a point-set construction of this trace map in the case of rings with involution, as carried out in Proposition A.1 below. In fact, we need very little from this trace map: since
![]() ${\mathrm {tr}}\colon {\mathrm {KR}}(k)\to {\mathrm {TCR}}(k;2)$
is a map of
${\mathrm {tr}}\colon {\mathrm {KR}}(k)\to {\mathrm {TCR}}(k;2)$
is a map of
![]() $\mathbb {Z}/2$
-equivariant spectra and
$\mathbb {Z}/2$
-equivariant spectra and
![]() ${\mathrm {W}}^{s}(k)\cong \pi _0{\mathrm {KR}}(k)^{\phi \mathbb {Z}/2}$
, it induces a commutative square
${\mathrm {W}}^{s}(k)\cong \pi _0{\mathrm {KR}}(k)^{\phi \mathbb {Z}/2}$
, it induces a commutative square
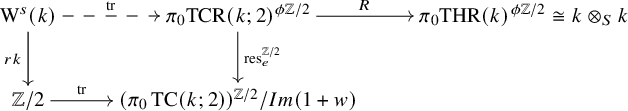
where the bottom map is induced by the usual trace map from [Reference Bökstedt, Hsiang and MadsenBHM93]. The composite on the top row sends the rank
![]() $1$
form
$1$
form
![]() $\langle a\rangle $
to
$\langle a\rangle $
to
![]() $a^{-1}\otimes a$
, as proved in Proposition A.1. It follows that the top trace map must be an isomorphism, and since the bottom map is a ring homomorphism and therefore injective, the respective vertical kernels I and K are then isomorphic.
$a^{-1}\otimes a$
, as proved in Proposition A.1. It follows that the top trace map must be an isomorphism, and since the bottom map is a ring homomorphism and therefore injective, the respective vertical kernels I and K are then isomorphic.
Remark 3.10. In the proof of Theorem 3.9, we are using the Milnor conjecture twice: once in order to identify
![]() $\nu ^\ast (k)$
with the graded ring of I, and then in order to identify I with the kernel of
$\nu ^\ast (k)$
with the graded ring of I, and then in order to identify I with the kernel of
![]() $\pi -\phi $
. It seems plausible that one could find a proof of the theorem which does not use Kato’s Theorems. Define W and T respectively as the equaliser and coequaliser of
$\pi -\phi $
. It seems plausible that one could find a proof of the theorem which does not use Kato’s Theorems. Define W and T respectively as the equaliser and coequaliser of
and K as the kernel of the multiplication map
![]() $\mu \colon W\to \mathbb {Z}/2$
. One can then try to directly show that the induced sequence
$\mu \colon W\to \mathbb {Z}/2$
. One can then try to directly show that the induced sequence
remains exact, where B is the subgroup of
![]() $k\otimes _Sk$
generated by the elements
$k\otimes _Sk$
generated by the elements
![]() $a\otimes b+b\otimes a$
. This would then prove Theorem 3.9 because, under the isomorphism
$a\otimes b+b\otimes a$
. This would then prove Theorem 3.9 because, under the isomorphism
![]() $\Omega ^\ast _k\cong J^\ast /J^{\ast +1}$
, the kernel of the middle map corresponds to
$\Omega ^\ast _k\cong J^\ast /J^{\ast +1}$
, the kernel of the middle map corresponds to
![]() $\nu ^\ast (k)$
, and the cokernel to
$\nu ^\ast (k)$
, and the cokernel to
![]() $\epsilon ^\ast (k)$
(see [Reference ArasonAra20, Fact 6]).
$\epsilon ^\ast (k)$
(see [Reference ArasonAra20, Fact 6]).
A The real trace map for rings with involution
Let us finish the paper with a construction of a
![]() $\mathbb {Z}/2$
-equivariant lift of the trace map
$\mathbb {Z}/2$
-equivariant lift of the trace map
![]() ${\mathrm {tr}}\colon {\mathrm {K}}\to {\mathrm {TC}}(-;p)$
, for every prime p. The trace was first constructed by Bökstedt-Hsiang-Madsen in [Reference Bökstedt, Hsiang and MadsenBHM93] as a natural transformation
${\mathrm {tr}}\colon {\mathrm {K}}\to {\mathrm {TC}}(-;p)$
, for every prime p. The trace was first constructed by Bökstedt-Hsiang-Madsen in [Reference Bökstedt, Hsiang and MadsenBHM93] as a natural transformation
![]() ${\mathrm {K}}\to {\mathrm {TC}}$
on the category of ring spectra. This construction has been extended to various settings, most notably as a natural transformation of functors from stable infinity categories; see, for example, [Reference Blumberg, Gepner and TabuadaBGT14].
${\mathrm {K}}\to {\mathrm {TC}}$
on the category of ring spectra. This construction has been extended to various settings, most notably as a natural transformation of functors from stable infinity categories; see, for example, [Reference Blumberg, Gepner and TabuadaBGT14].
A
![]() $\mathbb {Z}/2$
-equivariant extension of this map as a natural transformation
$\mathbb {Z}/2$
-equivariant extension of this map as a natural transformation
![]() ${\mathrm {KR}}\to {\mathrm {TCR}}$
of functors from Poincaré categories will appear in forthcoming work of Harpaz-Nikolaus-Shah [Reference Harpaz, Nikolaus and ShahHNS21]. For the purpose of this article, it will be more than sufficient to define the
${\mathrm {KR}}\to {\mathrm {TCR}}$
of functors from Poincaré categories will appear in forthcoming work of Harpaz-Nikolaus-Shah [Reference Harpaz, Nikolaus and ShahHNS21]. For the purpose of this article, it will be more than sufficient to define the
![]() $\mathbb {Z}/2$
-equivariant trace map on the category of discrete rings with involution. We will give a construction in line with the construction of the Dennis trace as carried out in [Reference MadsenMad94, §2.6]. After restricting down to
$\mathbb {Z}/2$
-equivariant trace map on the category of discrete rings with involution. We will give a construction in line with the construction of the Dennis trace as carried out in [Reference MadsenMad94, §2.6]. After restricting down to
![]() ${\mathrm {THR}}$
, this construction agrees with the one from [Reference Dotto and OgleDO19], which was defined for ring spectra with involution.
${\mathrm {THR}}$
, this construction agrees with the one from [Reference Dotto and OgleDO19], which was defined for ring spectra with involution.
Let A be a ring with involution
![]() $w\colon A^{op}\to A$
, and
$w\colon A^{op}\to A$
, and
![]() ${\mathrm {GL}}_n(A)$
the group of invertible
${\mathrm {GL}}_n(A)$
the group of invertible
![]() $n\times n$
-matrices with the involution that sends M to
$n\times n$
-matrices with the involution that sends M to
![]() $M^\ast :=w(M)^T$
, where
$M^\ast :=w(M)^T$
, where
![]() $(-)^T$
denotes the matrix transposition and w is applied to M entrywise. The set of fixed points of
$(-)^T$
denotes the matrix transposition and w is applied to M entrywise. The set of fixed points of
![]() ${\mathrm {GL}}_n(A)$
is the set of symmetric matrices
${\mathrm {GL}}_n(A)$
is the set of symmetric matrices
and
![]() ${\mathrm {GL}}_n(A)$
acts on it by
${\mathrm {GL}}_n(A)$
acts on it by
![]() $g\cdot M=gMg^\ast $
. We let
$g\cdot M=gMg^\ast $
. We let
![]() $B^\sigma {\mathrm {GL}}_n(A)$
be the classifying space
$B^\sigma {\mathrm {GL}}_n(A)$
be the classifying space
![]() $B{\mathrm {GL}}_n(A)$
with the involution of [Reference Burghelea and FiedorowiczBF84, Proposition 1.1.3]. Its
$B{\mathrm {GL}}_n(A)$
with the involution of [Reference Burghelea and FiedorowiczBF84, Proposition 1.1.3]. Its
![]() $\mathbb {Z}/2$
-fixed-points space is the bar construction of the action of
$\mathbb {Z}/2$
-fixed-points space is the bar construction of the action of
![]() ${\mathrm {GL}}_n(A)$
on
${\mathrm {GL}}_n(A)$
on
![]() ${\mathrm {GL}}_n(A)^{\mathbb {Z}/2}$
above (see also [Reference Dotto and OgleDO19, §2.1] for the details). For the purpose of this paper, we define
${\mathrm {GL}}_n(A)^{\mathbb {Z}/2}$
above (see also [Reference Dotto and OgleDO19, §2.1] for the details). For the purpose of this paper, we define
![]() ${\mathrm {KR}}(A)$
to be the
${\mathrm {KR}}(A)$
to be the
![]() $\mathbb {Z}/2$
-equivariant group-completion of the
$\mathbb {Z}/2$
-equivariant group-completion of the
![]() $\mathbb {Z}/2$
-equivariant
$\mathbb {Z}/2$
-equivariant
![]() $E_{\infty }$
-monoid with involution
$E_{\infty }$
-monoid with involution
where the monoid operation is induced by the direct sum of matrices. This is in fact the classifying space of the symmetric monoidal category with duality of finite dimensional free A-modules, and therefore indeed a
![]() $\mathbb {Z}/2$
-equivariant
$\mathbb {Z}/2$
-equivariant
![]() $E_{\infty }$
-monoid. By construction,
$E_{\infty }$
-monoid. By construction,
![]() $\pi _0({\mathrm {KR}}(A)^{\mathbb {Z}/2})$
is the group-completion of the commutative monoid
$\pi _0({\mathrm {KR}}(A)^{\mathbb {Z}/2})$
is the group-completion of the commutative monoid
which is the Grothendieck-Witt group
![]() ${\mathrm {GW}}^s(A)$
of symmetric forms of free A-modules. The transfer map is induced by the functor that sends a free module of rank n to the hyperbolic matrix of size
${\mathrm {GW}}^s(A)$
of symmetric forms of free A-modules. The transfer map is induced by the functor that sends a free module of rank n to the hyperbolic matrix of size
![]() $2n$
, and therefore,
$2n$
, and therefore,
![]() $\pi _0({\mathrm {KR}}(A)^{\phi \mathbb {Z}/2})$
is the symmetric Witt group
$\pi _0({\mathrm {KR}}(A)^{\phi \mathbb {Z}/2})$
is the symmetric Witt group
![]() $W^{s}(A)$
(again of free A-modules).
$W^{s}(A)$
(again of free A-modules).
Let us also recall from [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 5.1] that there is an isomorphism of abelian groups
where
![]() $A^{\mathbb {Z}/2}$
is the subgroup of fixed points of the involution w, and the quotient is by the subgroup T generated by the elements of the form (i) and (ii) from [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 5.1]. In particular, for
$A^{\mathbb {Z}/2}$
is the subgroup of fixed points of the involution w, and the quotient is by the subgroup T generated by the elements of the form (i) and (ii) from [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 5.1]. In particular, for
![]() $A=k$
a ring of characteristic
$A=k$
a ring of characteristic
![]() $2$
with trivial involution, this is
$2$
with trivial involution, this is
![]() $k\otimes _Sk$
, and since the transfer map
$k\otimes _Sk$
, and since the transfer map
![]() $(a+w(a))\otimes 1$
of [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 5.1] is in this case zero, we have as well that
$(a+w(a))\otimes 1$
of [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 5.1] is in this case zero, we have as well that
![]() $\pi _0({\mathrm {THR}}(k)^{\phi \mathbb {Z}/2})\cong k\otimes _Sk$
.
$\pi _0({\mathrm {THR}}(k)^{\phi \mathbb {Z}/2})\cong k\otimes _Sk$
.
Proposition A.1. Let A be a ring with involution. For every prime p, there is a map of
![]() $\mathbb {Z}/2$
-spectra
$\mathbb {Z}/2$
-spectra
![]() ${\mathrm {tr}}\colon {\mathrm {KR}}(A)\to {\mathrm {TCR}}(A;p)$
which forgets to the K-theoretic trace map of [Reference Bökstedt, Hsiang and MadsenBHM93]. The composite
${\mathrm {tr}}\colon {\mathrm {KR}}(A)\to {\mathrm {TCR}}(A;p)$
which forgets to the K-theoretic trace map of [Reference Bökstedt, Hsiang and MadsenBHM93]. The composite
sends the element of
![]() ${\mathrm {GW}}^s(A)$
represented by a symmetric form x on
${\mathrm {GW}}^s(A)$
represented by a symmetric form x on
![]() $A^{\oplus n}$
to
$A^{\oplus n}$
to
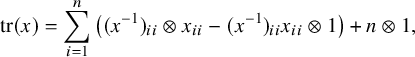 $$\begin{align*}{\mathrm{tr}}(x)=\sum_{i=1}^n\big((x^{-1})_{ii}\otimes x_{ii}-(x^{-1})_{ii}x_{ii}\otimes 1\big)+n\otimes 1, \end{align*}$$
$$\begin{align*}{\mathrm{tr}}(x)=\sum_{i=1}^n\big((x^{-1})_{ii}\otimes x_{ii}-(x^{-1})_{ii}x_{ii}\otimes 1\big)+n\otimes 1, \end{align*}$$
where
![]() $x_{ii}$
are the entries of the matrix of x for the standard basis of
$x_{ii}$
are the entries of the matrix of x for the standard basis of
![]() $A^{\oplus n}$
, and
$A^{\oplus n}$
, and
![]() $x^{-1}$
denotes the inverse matrix.
$x^{-1}$
denotes the inverse matrix.
Proof. We construct the trace by employing a construction completely analogous to the one from Dennis and Bökstedt-Hsiang-Madsen, as explained in [Reference MadsenMad94, §2.6]. Let
![]() $B^{di}{\mathrm {GL}}_n(A)$
be the dihedral bar construction of
$B^{di}{\mathrm {GL}}_n(A)$
be the dihedral bar construction of
![]() ${\mathrm {GL}}_n(A)$
, defined as the geometric realisation of the dihedral nerve
${\mathrm {GL}}_n(A)$
, defined as the geometric realisation of the dihedral nerve
![]() $N^{di}{\mathrm {GL}}_n(A)$
, which is the cyclic nerve of
$N^{di}{\mathrm {GL}}_n(A)$
, which is the cyclic nerve of
![]() ${\mathrm {GL}}_n(A)$
with the involution analogous to the one of
${\mathrm {GL}}_n(A)$
with the involution analogous to the one of
![]() ${\mathrm {THR}}(k)$
from §1. Its
${\mathrm {THR}}(k)$
from §1. Its
![]() $\mathbb {Z}/2$
-fixed-points space is the two-sided bar construction of the action of
$\mathbb {Z}/2$
-fixed-points space is the two-sided bar construction of the action of
![]() ${\mathrm {GL}}_n(A)$
on
${\mathrm {GL}}_n(A)$
on
![]() ${\mathrm {GL}}_n(A)^{\mathbb {Z}/2}$
, and we refer to [Reference Dotto and OgleDO19, §2.1] for the details.
${\mathrm {GL}}_n(A)^{\mathbb {Z}/2}$
, and we refer to [Reference Dotto and OgleDO19, §2.1] for the details.
We define the trace map from maps of
![]() $\mathbb {Z}/2$
-spaces
$\mathbb {Z}/2$
-spaces
for every
![]() $r\geq 1$
, by taking the disjoint union over
$r\geq 1$
, by taking the disjoint union over
![]() $n\geq 0$
and group-completing the source with respect to direct sums. The maps in this composite are defined as follows. The map s is the canonical section, which is defined on an n-simplex
$n\geq 0$
and group-completing the source with respect to direct sums. The maps in this composite are defined as follows. The map s is the canonical section, which is defined on an n-simplex
![]() $(g_1, \dots , g_n)$
by
$(g_1, \dots , g_n)$
by
The second map of (A.1) is the inclusion of invertible matrices into the monoid of all
![]() $(n\times n)$
-matrices
$(n\times n)$
-matrices
![]() ${\mathrm {M}}_n(A)$
, again with the transposition of matrices and entrywise w as involution. For the third map, we use that
${\mathrm {M}}_n(A)$
, again with the transposition of matrices and entrywise w as involution. For the third map, we use that
![]() $B^{di}{\mathrm {M}}_n(A)$
is the geometric realisation of the dihedral nerve
$B^{di}{\mathrm {M}}_n(A)$
is the geometric realisation of the dihedral nerve
![]() $N^{di}{\mathrm {M}}_n(A)$
, and therefore has an action of the dihedral group
$N^{di}{\mathrm {M}}_n(A)$
, and therefore has an action of the dihedral group
![]() $D_r$
of order
$D_r$
of order
![]() $2r$
, for every integer
$2r$
, for every integer
![]() $r\geq 1$
. The realisation of the r-subdivision
$r\geq 1$
. The realisation of the r-subdivision
![]() ${\mathrm {sd}}_r$
of [Reference Bökstedt, Hsiang and MadsenBHM93, §1] applied to the dihedral nerve
${\mathrm {sd}}_r$
of [Reference Bökstedt, Hsiang and MadsenBHM93, §1] applied to the dihedral nerve
![]() $N^{di}{\mathrm {M}}_n(A)$
has a
$N^{di}{\mathrm {M}}_n(A)$
has a
![]() $\mathbb {Z}/2$
-action, and its geometric realisation is
$\mathbb {Z}/2$
-action, and its geometric realisation is
![]() $D_r$
-equivariantly isomorphic to
$D_r$
-equivariantly isomorphic to
![]() $B^{di}{\mathrm {M}}_n(A)$
(see [Reference Dotto, Moi and PatchkoriaDMP24, §1.2] for a detailed discussion about subdivisions of dihedral objects). Thus, we obtain
$B^{di}{\mathrm {M}}_n(A)$
(see [Reference Dotto, Moi and PatchkoriaDMP24, §1.2] for a detailed discussion about subdivisions of dihedral objects). Thus, we obtain
![]() $\mathbb {Z}/2$
-equivariant isomorphisms
$\mathbb {Z}/2$
-equivariant isomorphisms
where the first map is induced by the diagonal map degreewise, and the second map is the canonical isomorphism
![]() $E_r\colon |{\mathrm {sd}}_rX|\to |X|$
for a dihedral set X, from [Reference Bökstedt, Hsiang and MadsenBHM93, Lemma 1.1] (which is denoted by
$E_r\colon |{\mathrm {sd}}_rX|\to |X|$
for a dihedral set X, from [Reference Bökstedt, Hsiang and MadsenBHM93, Lemma 1.1] (which is denoted by
![]() $D_r$
there). By denoting
$D_r$
there). By denoting
![]() $\Delta ^k$
the standard k-simplex space
$\Delta ^k$
the standard k-simplex space
the map
![]() $E_r$
sends the equivalence class of
$E_r$
sends the equivalence class of
![]() $(x;t)$
, with
$(x;t)$
, with
![]() $x\in ({\mathrm {sd}}_rX)_k=X_{r(k+1)-1}$
and
$x\in ({\mathrm {sd}}_rX)_k=X_{r(k+1)-1}$
and
![]() $t\in \Delta ^{k}$
, to the class of
$t\in \Delta ^{k}$
, to the class of
![]() $(x;\delta _r(t))$
, where
$(x;\delta _r(t))$
, where
![]() $\delta _r\colon \Delta ^{k}\to \Delta ^{r(k+1)-1}$
sends t to
$\delta _r\colon \Delta ^{k}\to \Delta ^{r(k+1)-1}$
sends t to
![]() $(t, \dots , t)/r$
(with r-many components). The third map of (A.1) is then defined to be the adjoint of the composite of the maps of
$(t, \dots , t)/r$
(with r-many components). The third map of (A.1) is then defined to be the adjoint of the composite of the maps of
![]() $\mathbb {Z}/2$
-spectra
$\mathbb {Z}/2$
-spectra
which are respectively
![]() $\Sigma ^\infty _+(E_r\Delta _r)$
, the tom Dieck splitting, the monoidality of the equivariant suspension spectrum functor, and the Hurewicz map. Finally, the last map of (A.1) is induced by the inclusion of A into
$\Sigma ^\infty _+(E_r\Delta _r)$
, the tom Dieck splitting, the monoidality of the equivariant suspension spectrum functor, and the Hurewicz map. Finally, the last map of (A.1) is induced by the inclusion of A into
![]() ${\mathrm {M}}_n(A)$
as
${\mathrm {M}}_n(A)$
as
![]() $(1, 1)$
-entry, and it is a
$(1, 1)$
-entry, and it is a
![]() $\mathbb {Z}/2$
-equivalence by [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 4.9] (which visibly restricts to
$\mathbb {Z}/2$
-equivalence by [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 4.9] (which visibly restricts to
![]() $C_r$
-fixed points).
$C_r$
-fixed points).
A direct verification shows that the map of (A.1) is compatible with the direct sum of matrices and with its symmetry isomorphism, and therefore by setting
![]() $r=p^{m-1}$
, we obtain a map of
$r=p^{m-1}$
, we obtain a map of
![]() $\mathbb {Z}/2$
-spectra
$\mathbb {Z}/2$
-spectra
for every integer
![]() $m\geq 1$
and prime p. To obtain a map to
$m\geq 1$
and prime p. To obtain a map to
![]() ${\mathrm {TCR}}(A;p)$
we need to show that the maps
${\mathrm {TCR}}(A;p)$
we need to show that the maps
![]() ${\mathrm {tr}}^m$
are compatible with the restriction and Frobenius
${\mathrm {tr}}^m$
are compatible with the restriction and Frobenius
![]() $R, F\colon {\mathrm {TRR}}^{m+1}(A;p)\to {\mathrm {TRR}}^{m}(A;p)$
. Unravelling the definitions, it is sufficient to provide
$R, F\colon {\mathrm {TRR}}^{m+1}(A;p)\to {\mathrm {TRR}}^{m}(A;p)$
. Unravelling the definitions, it is sufficient to provide
![]() $\mathbb {Z}/2$
-equivariant homotopies between the composites from the bottom left to the bottom right
$\mathbb {Z}/2$
-equivariant homotopies between the composites from the bottom left to the bottom right
![]() $\mathbb {Z}/2$
-spaces of the diagram
$\mathbb {Z}/2$
-spaces of the diagram
The vertical map R is defined by identifying the
![]() $C_p$
-fixed points of the
$C_p$
-fixed points of the
![]() $p^m$
-fold subdivision with the
$p^m$
-fold subdivision with the
![]() $p^{m-1}$
-fold subdivision, and then taking
$p^{m-1}$
-fold subdivision, and then taking
![]() $C_{p^{m-1}}$
-fixed points. It follows from [Reference Bökstedt, Hsiang and MadsenBHM93, (1.12)] that the inner most triangle commutes strictly. The vertical map F is the inclusion of fixed points. To see how the outer triangle commutes when restricted along s, we decompose the diagram as
$C_{p^{m-1}}$
-fixed points. It follows from [Reference Bökstedt, Hsiang and MadsenBHM93, (1.12)] that the inner most triangle commutes strictly. The vertical map F is the inclusion of fixed points. To see how the outer triangle commutes when restricted along s, we decompose the diagram as
where the unlabelled map is the inclusion of fixed points. The lower right triangle commutes by [Reference Bökstedt, Hsiang and MadsenBHM93, (1.12)], and the square above it by naturality of the inclusion of fixed points. We then need to define a
![]() $\mathbb {Z}/2$
-equivariant homotopy that makes the the triangle on the left commute when restricted along s. By factoring
$\mathbb {Z}/2$
-equivariant homotopy that makes the the triangle on the left commute when restricted along s. By factoring
![]() $\Delta _{p^{m}}=\Delta _{p^{m-1}}\circ \Delta _p$
, it is sufficient to treat the case where
$\Delta _{p^{m}}=\Delta _{p^{m-1}}\circ \Delta _p$
, it is sufficient to treat the case where
![]() $m=1$
. The homotopy provided in [Reference Bökstedt, Hsiang and MadsenBHM93, Proposition 2.5] is not quite
$m=1$
. The homotopy provided in [Reference Bökstedt, Hsiang and MadsenBHM93, Proposition 2.5] is not quite
![]() $\mathbb {Z}/2$
-equivariant, but we can use a small variation of it. Let us define
$\mathbb {Z}/2$
-equivariant, but we can use a small variation of it. Let us define
![]() $h_k\colon \Delta ^k\times [0, 1]\to \Delta ^{p(k+1)-1}$
for every
$h_k\colon \Delta ^k\times [0, 1]\to \Delta ^{p(k+1)-1}$
for every
![]() $k\geq 0$
, by
$k\geq 0$
, by
where the right-hand side has p components. If we apply the subdivision
![]() ${\mathrm {sd}}_e$
as in [Reference Dotto, Moi and PatchkoriaDMP24, §1.2] to make the
${\mathrm {sd}}_e$
as in [Reference Dotto, Moi and PatchkoriaDMP24, §1.2] to make the
![]() $\mathbb {Z}/2$
-actions on the spaces of the diagram simplicial, the upper composite sends the equivalence class of
$\mathbb {Z}/2$
-actions on the spaces of the diagram simplicial, the upper composite sends the equivalence class of
![]() $(g_1, \dots , g_{2k+1};t)$
, with
$(g_1, \dots , g_{2k+1};t)$
, with
![]() $(g_1, \dots , g_{2k+1})$
a k-simplex of
$(g_1, \dots , g_{2k+1})$
a k-simplex of
![]() ${\mathrm {sd}}_eN^{\sigma }{\mathrm {GL}}_n(A)$
and
${\mathrm {sd}}_eN^{\sigma }{\mathrm {GL}}_n(A)$
and
![]() $t\in \Delta ^k$
, to the equivalence class of
$t\in \Delta ^k$
, to the equivalence class of
The lower composite is simply the functor
![]() ${\mathrm {sd}}_e$
applied to the section s. Thus, by sending the same equivalence class to the class of
${\mathrm {sd}}_e$
applied to the section s. Thus, by sending the same equivalence class to the class of
![]() $(\Delta _{p}((g_1\dots g_{2k+1})^{-1}, g_1, \dots , g_{2k+1});h_k(s, t))$
, we obtain a
$(\Delta _{p}((g_1\dots g_{2k+1})^{-1}, g_1, \dots , g_{2k+1});h_k(s, t))$
, we obtain a
![]() $\mathbb {Z}/2$
-equivariant homotopy from the upper composite to
$\mathbb {Z}/2$
-equivariant homotopy from the upper composite to
where each
![]() $0$
on the left is the zero vertex of
$0$
on the left is the zero vertex of
![]() $\Delta ^k$
, and
$\Delta ^k$
, and
![]() $d_l$
is the last face map of
$d_l$
is the last face map of
![]() ${\mathrm {sd}}_eN^{di}{\mathrm {M}}_n(A)$
. Since this last face map multiplies the central three components
${\mathrm {sd}}_eN^{di}{\mathrm {M}}_n(A)$
. Since this last face map multiplies the central three components
![]() $a_q, a_{q+1}$
and
$a_q, a_{q+1}$
and
![]() $a_{q+2}$
of a q-simplex
$a_{q+2}$
of a q-simplex
![]() $(a_0, \dots , a_{2q+1})$
of
$(a_0, \dots , a_{2q+1})$
of
![]() ${\mathrm {sd}}_eN^{di}{\mathrm {M}}_n(A)$
, we find that, by denoting
${\mathrm {sd}}_eN^{di}{\mathrm {M}}_n(A)$
, we find that, by denoting
![]() $g_0:=(g_1\dots g_{2k+1})^{-1}$
,
$g_0:=(g_1\dots g_{2k+1})^{-1}$
,
The middle entry is equal to
![]() $g_{k+1}$
since
$g_{k+1}$
since
![]() $g_0=(g_1\dots g_{2k+1})^{-1}$
, and it follows that the end of the homotopy is indeed the subdivision of s. We can therefore lift
$g_0=(g_1\dots g_{2k+1})^{-1}$
, and it follows that the end of the homotopy is indeed the subdivision of s. We can therefore lift
![]() ${\mathrm {tr}}^m$
along R and F to obtain a map of
${\mathrm {tr}}^m$
along R and F to obtain a map of
![]() $\mathbb {Z}/2$
-spectra
$\mathbb {Z}/2$
-spectra
![]() ${\mathrm {tr}}\colon {\mathrm {KR}}(A)\to {\mathrm {TCR}}(A;p)$
, for every prime p.
${\mathrm {tr}}\colon {\mathrm {KR}}(A)\to {\mathrm {TCR}}(A;p)$
, for every prime p.
Let us now identify the effect of the trace in
![]() $\pi _0$
of the fixed points. By construction, if we compose
$\pi _0$
of the fixed points. By construction, if we compose
![]() ${\mathrm {tr}}$
with the map R all the way to
${\mathrm {tr}}$
with the map R all the way to
![]() ${\mathrm {THR}}(A)$
we recover the map
${\mathrm {THR}}(A)$
we recover the map
![]() ${\mathrm {tr}}^0\colon {\mathrm {KR}}(A)\to {\mathrm {THR}}(A)$
. Thus, for this calculation, we need to describe the map (A.1) for
${\mathrm {tr}}^0\colon {\mathrm {KR}}(A)\to {\mathrm {THR}}(A)$
. Thus, for this calculation, we need to describe the map (A.1) for
![]() $r=1$
. On fixed points, the map s is the map of bar constructions
$r=1$
. On fixed points, the map s is the map of bar constructions
which sends a k-simplex
![]() $(g_1, \dots , g_k, x)$
, with
$(g_1, \dots , g_k, x)$
, with
![]() $g_i\in {\mathrm {GL}}_n(A)$
and
$g_i\in {\mathrm {GL}}_n(A)$
and
![]() $x\in {\mathrm {GL}}_n(A)^{\mathbb {Z}/2}$
, to
$x\in {\mathrm {GL}}_n(A)^{\mathbb {Z}/2}$
, to
where
![]() $(-)^\ast $
denotes the involution on
$(-)^\ast $
denotes the involution on
![]() ${\mathrm {GL}}_n(A)$
. Thus, after applying
${\mathrm {GL}}_n(A)$
. Thus, after applying
![]() $\pi _0$
and identifying the components of
$\pi _0$
and identifying the components of
![]() ${\mathrm {THR}}$
using [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 5.1], the map of (A.1) becomes a map
${\mathrm {THR}}$
using [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 5.1], the map of (A.1) becomes a map
where the quotients on the two sets on the left are for the respective actions of
![]() ${\mathrm {GL}}_n(A)$
. By the calculation of s above, this map sends the isomorphism class of a form of rank n, represented by a matrix
${\mathrm {GL}}_n(A)$
. By the calculation of s above, this map sends the isomorphism class of a form of rank n, represented by a matrix
![]() $x\in {\mathrm {GL}}_n(A)^{\mathbb {Z}/2}$
, to
$x\in {\mathrm {GL}}_n(A)^{\mathbb {Z}/2}$
, to
![]() $m(x^{-1}\otimes x)$
. For the proof of Theorem 3.9, we were only interested in rank
$m(x^{-1}\otimes x)$
. For the proof of Theorem 3.9, we were only interested in rank
![]() $1$
forms (since these generate the Witt group of a field), and since for
$1$
forms (since these generate the Witt group of a field), and since for
![]() $n=1$
the map m is the identity, we immediately find that the class of a symmetric form determined by a unit a of A fixed by the involution is sent to
$n=1$
the map m is the identity, we immediately find that the class of a symmetric form determined by a unit a of A fixed by the involution is sent to
![]() $a^{-1}\otimes a$
.
$a^{-1}\otimes a$
.
For larger values of n, we need to determine the isomorphism
Let us decompose a symmetric matrix
![]() $M\in {\mathrm {M}}_n(A)^{\mathbb {Z}/2}$
as
$M\in {\mathrm {M}}_n(A)^{\mathbb {Z}/2}$
as
![]() $M=\sum _{i=1}^nM_{ii}e_{ii}+\sum _{1\leq i<j\leq n}(M_{ij}e_{ij}+w(M_{ij})e_{ji}),$
where
$M=\sum _{i=1}^nM_{ii}e_{ii}+\sum _{1\leq i<j\leq n}(M_{ij}e_{ij}+w(M_{ij})e_{ji}),$
where
![]() $e_{ij}$
is the canonical basis element with
$e_{ij}$
is the canonical basis element with
![]() $1$
in the entry
$1$
in the entry
![]() $(i, j)$
and with all the other entries equal to zero. By regarding the abelian group with involution
$(i, j)$
and with all the other entries equal to zero. By regarding the abelian group with involution
![]() ${\mathrm {M}}_n(A)$
as a Mackey functor, we can then write the fixed point M as
${\mathrm {M}}_n(A)$
as a Mackey functor, we can then write the fixed point M as
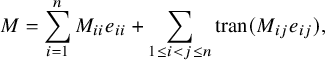 $$\begin{align*}M=\sum_{i=1}^nM_{ii}e_{ii}+\sum_{1\leq i<j\leq n}{\mathrm{tran}}(M_{ij}e_{ij}), \end{align*}$$
$$\begin{align*}M=\sum_{i=1}^nM_{ii}e_{ii}+\sum_{1\leq i<j\leq n}{\mathrm{tran}}(M_{ij}e_{ij}), \end{align*}$$
where
![]() ${\mathrm {tran}}$
denotes the transfer map of the Mackey functor, which sends a matrix N to
${\mathrm {tran}}$
denotes the transfer map of the Mackey functor, which sends a matrix N to
![]() $N+N^\ast $
. By applying the same decomposition to a second fixed point
$N+N^\ast $
. By applying the same decomposition to a second fixed point
![]() $M^{\prime }\in {\mathrm {M}}_n(A)^{\mathbb {Z}/2}$
, we find that
$M^{\prime }\in {\mathrm {M}}_n(A)^{\mathbb {Z}/2}$
, we find that
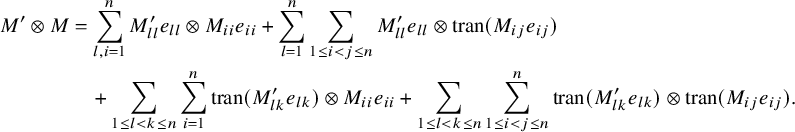 $$ \begin{align*} M^{\prime}\otimes M&=\sum_{l, i=1}^nM^{\prime}_{ll}e_{ll}\otimes M_{ii}e_{ii}+\sum_{l=1}^n\sum_{1\leq i<j\leq n}M^{\prime}_{ll}e_{ll}\otimes{\mathrm{tran}}(M_{ij}e_{ij}) \\&\quad+\sum_{1\leq l<k\leq n}\sum_{i=1}^n{\mathrm{tran}}(M^{\prime}_{lk}e_{lk})\otimes M_{ii}e_{ii}+\sum_{1\leq l<k\leq n}\sum_{1\leq i<j\leq n}^n{\mathrm{tran}}(M^{\prime}_{lk}e_{lk})\otimes{\mathrm{tran}}(M_{ij}e_{ij}). \end{align*} $$
$$ \begin{align*} M^{\prime}\otimes M&=\sum_{l, i=1}^nM^{\prime}_{ll}e_{ll}\otimes M_{ii}e_{ii}+\sum_{l=1}^n\sum_{1\leq i<j\leq n}M^{\prime}_{ll}e_{ll}\otimes{\mathrm{tran}}(M_{ij}e_{ij}) \\&\quad+\sum_{1\leq l<k\leq n}\sum_{i=1}^n{\mathrm{tran}}(M^{\prime}_{lk}e_{lk})\otimes M_{ii}e_{ii}+\sum_{1\leq l<k\leq n}\sum_{1\leq i<j\leq n}^n{\mathrm{tran}}(M^{\prime}_{lk}e_{lk})\otimes{\mathrm{tran}}(M_{ij}e_{ij}). \end{align*} $$
By the relation (ii) of [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 5.1] defining the subgroup T, this is equivalent to
 $$ \begin{align*} M^{\prime}\otimes M&=\sum_{l, i=1}^nM^{\prime}_{ll}e_{ll}\otimes M_{ii}e_{ii}+\sum_{l=1}^n\sum_{1\leq i<j\leq n}{\mathrm{tran}}(M^{\prime}_{ll}e_{ll} M_{ij}e_{ij}) \otimes 1 \\ &+\sum_{1\leq l<k\leq n}\sum_{i=1}^n1\otimes {\mathrm{tran}}(M^{\prime}_{lk}e_{lk}M_{ii}e_{ii})+\sum_{1\leq l<k\leq n}\sum_{1\leq i<j\leq n}{\mathrm{tran}}(M^{\prime}_{lk}e_{lk}(M_{ij}e_{ij}+w(M_{ij})e_{ji}))\otimes 1 \\ &=\sum_{l, i=1}^nM^{\prime}_{ll}e_{ll}\otimes M_{ii}e_{ii}+\sum_{1\leq i<j\leq n}{\mathrm{tran}}(M^{\prime}_{ii}M_{ij}e_{ij})\otimes 1+\sum_{1\leq l<k\leq n}1\otimes {\mathrm{tran}}(M^{\prime}_{lk}M_{kk}e_{lk}) \\ &+\sum_{1\leq l<k<j\leq n}{\mathrm{tran}}(M^{\prime}_{lk}M_{kj}e_{lj})\otimes 1 +\sum_{1\leq l, i<k\leq n}{\mathrm{tran}}(M^{\prime}_{lk}w(M_{ik})e_{li})\otimes 1, \end{align*} $$
$$ \begin{align*} M^{\prime}\otimes M&=\sum_{l, i=1}^nM^{\prime}_{ll}e_{ll}\otimes M_{ii}e_{ii}+\sum_{l=1}^n\sum_{1\leq i<j\leq n}{\mathrm{tran}}(M^{\prime}_{ll}e_{ll} M_{ij}e_{ij}) \otimes 1 \\ &+\sum_{1\leq l<k\leq n}\sum_{i=1}^n1\otimes {\mathrm{tran}}(M^{\prime}_{lk}e_{lk}M_{ii}e_{ii})+\sum_{1\leq l<k\leq n}\sum_{1\leq i<j\leq n}{\mathrm{tran}}(M^{\prime}_{lk}e_{lk}(M_{ij}e_{ij}+w(M_{ij})e_{ji}))\otimes 1 \\ &=\sum_{l, i=1}^nM^{\prime}_{ll}e_{ll}\otimes M_{ii}e_{ii}+\sum_{1\leq i<j\leq n}{\mathrm{tran}}(M^{\prime}_{ii}M_{ij}e_{ij})\otimes 1+\sum_{1\leq l<k\leq n}1\otimes {\mathrm{tran}}(M^{\prime}_{lk}M_{kk}e_{lk}) \\ &+\sum_{1\leq l<k<j\leq n}{\mathrm{tran}}(M^{\prime}_{lk}M_{kj}e_{lj})\otimes 1 +\sum_{1\leq l, i<k\leq n}{\mathrm{tran}}(M^{\prime}_{lk}w(M_{ik})e_{li})\otimes 1, \end{align*} $$
where the last equality follows from carrying out the matrix multiplication on the canonical basis. Again by [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 5.1], the transfer map of the Mackey functor
![]() $\underline {\pi }_0 {\mathrm {THR}}({\mathrm {M}}_n(A))$
sends the equivalence class of a matrix M in
$\underline {\pi }_0 {\mathrm {THR}}({\mathrm {M}}_n(A))$
sends the equivalence class of a matrix M in
![]() $\pi _0{\mathrm {THH}}({\mathrm {M}}_n(A))\cong {\mathrm {M}}_n(A)/[{\mathrm {M}}_n(A), {\mathrm {M}}_n(A)]$
, to
$\pi _0{\mathrm {THH}}({\mathrm {M}}_n(A))\cong {\mathrm {M}}_n(A)/[{\mathrm {M}}_n(A), {\mathrm {M}}_n(A)]$
, to
![]() $1\otimes {\mathrm {tran}}(M)={\mathrm {tran}}(M)\otimes 1$
in
$1\otimes {\mathrm {tran}}(M)={\mathrm {tran}}(M)\otimes 1$
in
![]() $({\mathrm {M}}_n(A)^{\mathbb {Z}/2}\otimes {\mathrm {M}}_n(A)^{\mathbb {Z}/2})/T$
. The map m from [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 4.9] is a map of
$({\mathrm {M}}_n(A)^{\mathbb {Z}/2}\otimes {\mathrm {M}}_n(A)^{\mathbb {Z}/2})/T$
. The map m from [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Theorem 4.9] is a map of
![]() $\mathbb {Z}/2$
-spectra, and therefore, it commutes with the transfer. Moreover, since the underlying map of spectra is the trace map of [Reference Bökstedt, Hsiang and MadsenBHM93], in
$\mathbb {Z}/2$
-spectra, and therefore, it commutes with the transfer. Moreover, since the underlying map of spectra is the trace map of [Reference Bökstedt, Hsiang and MadsenBHM93], in
![]() $\pi _0$
it sends a matrix to its trace, and therefore, the terms involving
$\pi _0$
it sends a matrix to its trace, and therefore, the terms involving
![]() $e_{ij}$
vanish for
$e_{ij}$
vanish for
![]() $i\neq j$
. We then find that
$i\neq j$
. We then find that
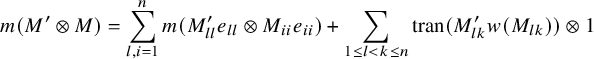 $$ \begin{align*} m(M^{\prime}\otimes M) &=\sum_{l, i=1}^nm(M^{\prime}_{ll}e_{ll}\otimes M_{ii}e_{ii})+\sum_{1\leq l<k\leq n}{\mathrm{tran}}(M^{\prime}_{lk}w(M_{lk}))\otimes 1 \end{align*} $$
$$ \begin{align*} m(M^{\prime}\otimes M) &=\sum_{l, i=1}^nm(M^{\prime}_{ll}e_{ll}\otimes M_{ii}e_{ii})+\sum_{1\leq l<k\leq n}{\mathrm{tran}}(M^{\prime}_{lk}w(M_{lk}))\otimes 1 \end{align*} $$
in
![]() $(A^{\mathbb {Z}/2}\otimes A^{\mathbb {Z}/2})/T$
. By the definition of m of [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Proof of Theorem 4.9], it sends
$(A^{\mathbb {Z}/2}\otimes A^{\mathbb {Z}/2})/T$
. By the definition of m of [Reference Dotto, Moi, Patchkoria and ReehDMPR21, Proof of Theorem 4.9], it sends
![]() $e_{ij}\otimes e_{lk}$
to
$e_{ij}\otimes e_{lk}$
to
![]() $1$
if
$1$
if
![]() $j=l$
and
$j=l$
and
![]() $k=i$
, and to zero otherwise. Thus,
$k=i$
, and to zero otherwise. Thus,
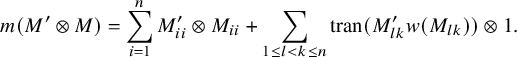 $$ \begin{align*} m(M^{\prime}\otimes M) &=\sum_{i=1}^nM^{\prime}_{ii}\otimes M_{ii}+\sum_{1\leq l<k\leq n}{\mathrm{tran}}(M^{\prime}_{lk}w(M_{lk}))\otimes 1. \end{align*} $$
$$ \begin{align*} m(M^{\prime}\otimes M) &=\sum_{i=1}^nM^{\prime}_{ii}\otimes M_{ii}+\sum_{1\leq l<k\leq n}{\mathrm{tran}}(M^{\prime}_{lk}w(M_{lk}))\otimes 1. \end{align*} $$
Since M is symmetric (i.e.,
![]() $w(M_{lk})=M_{kl}$
), we may write this expression as
$w(M_{lk})=M_{kl}$
), we may write this expression as
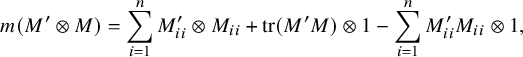 $$ \begin{align*} m(M^{\prime}\otimes M) &=\sum_{i=1}^nM^{\prime}_{ii}\otimes M_{ii}+{\mathrm{tr}}(M^{\prime}M)\otimes 1-\sum_{i=1}^nM^{\prime}_{ii}M_{ii}\otimes 1, \end{align*} $$
$$ \begin{align*} m(M^{\prime}\otimes M) &=\sum_{i=1}^nM^{\prime}_{ii}\otimes M_{ii}+{\mathrm{tr}}(M^{\prime}M)\otimes 1-\sum_{i=1}^nM^{\prime}_{ii}M_{ii}\otimes 1, \end{align*} $$
where
![]() ${\mathrm {tr}}$
denotes the usual trace of a matrix. When
${\mathrm {tr}}$
denotes the usual trace of a matrix. When
![]() $M^{\prime }\otimes M=x^{-1}\otimes x$
for some
$M^{\prime }\otimes M=x^{-1}\otimes x$
for some
![]() $x\in {\mathrm {GL}}_n(A)^{\mathbb {Z}/2}$
, this gives the formula we wanted.
$x\in {\mathrm {GL}}_n(A)^{\mathbb {Z}/2}$
, this gives the formula we wanted.
Acknowledgements
I genuinely thank Ib Madsen for encouraging me to look into a possible relation between real THH and the Milnor conjecture, which eventually led to the ideas of this paper. I also thank Irakli Patchkoria, Thomas Read and Damiano Testa for helpful conversations regarding some technical aspects of the project.
Competing interest
None.
Funding statement
This research was supported by the Engineering and Physical Sciences Research Council (EPSRC), grant EP/W019620/1.