Hostname: page-component-5b777bbd6c-v47t2 Total loading time: 0 Render date: 2025-06-21T02:21:00.013Z Has data issue: false hasContentIssue false
  • English
  • Français

DICHROMATIC NUMBER AND FRACTIONAL CHROMATIC NUMBER

Part of: Graph theory

Published online by Cambridge University Press:  15 December 2016

BOJAN MOHAR  and
HEHUI WU
BOJAN MOHAR
Affiliation:
Department of Mathematics, Simon Fraser University, Burnaby, BC V5A 1S6, Canada; mohar@sfu.ca
HEHUI WU
Affiliation:
2202 East Guanghua Tower, Fudan University, 220 Handan Road, Shanghai, China 200433; hhwu@fudan.edu.cn Department of Mathematics, University of Mississippi, Oxford, MS 38677, USA

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The dichromatic number of a graph 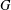$G$ is the maximum integer 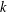$k$ such that there exists an orientation of the edges of 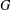$G$ such that for every partition of the vertices into fewer than 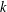$k$ parts, at least one of the parts must contain a directed cycle under this orientation. In 1979, Erdős and Neumann-Lara conjectured that if the dichromatic number of a graph is bounded, so is its chromatic number. We make the first significant progress on this conjecture by proving a fractional version of the conjecture. While our result uses a stronger assumption about the fractional chromatic number, it also gives a much stronger conclusion: if the fractional chromatic number of a graph is at least $t$ , then the fractional version of the dichromatic number of the graph is at least 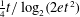${\textstyle \frac{1}{4}}t/\log _{2}(2et^{2})$ . This bound is best possible up to a small constant factor. Several related results of independent interest are given.

MSC classification

Primary: 05C15: Coloring of graphs and hypergraphs
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 4 , 2016 , e32
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2016

References

Berger, E., Choromanski, K., Chudnovsky, M., Fox, J., Loebl, M., Scott, A., Seymour, P. and Thomassé, S., ‘Tournaments and coloring’, J. Combin. Theory B 103 (2013), 1–20.Google Scholar
Bokal, D., Fijavž, G., Juvan, M., Kayll, P. M. and Mohar, B., ‘The circular chromatic number of a digraph’, J. Graph Theory 46 (2004), 227–240.Google Scholar
Chudnovsky, M., ‘The Erdős–Hajnal conjecture—A Survey’, J. Graph Theory 75 (2014), 178–190.Google Scholar
Erdős, P., ‘Problems and results in number theory and graph theory’, inProceedings of Ninth Manitoba Conference on Numerical Math. and Computing, 1979, pp. 3–21 https://www.renyi.hu/∼p_erdos/1980-30.pdf.Google Scholar
Erdős, P., Gimbel, J. and Kratsch, D., ‘Some extremal results in cochromatic and dichromatic theory’, J. Graph Theory 15(6) (1991), 579–585.Google Scholar
Godsil, C. and Royle, G., Algebraic Graph Theory, Graduate Texts in Mathematics, 207 (Springer, New York, 2001).CrossRefGoogle Scholar
Harutyunyan, A. and Mohar, B., ‘Two results on the digraph chromatic number’, Discrete Math. 312(10) (2012), 1823–1826.Google Scholar
Lovász, L., ‘Kneser’s conjecture, chromatic number, and homotopy’, J. Combin. Theory A 25 (1978), 319–324.Google Scholar
Mohar, B., ‘Circular colorings of edge-weighted graphs’, J. Graph Theory 43 (2003), 107–116.Google Scholar
Neumann-Lara, V., ‘The dichromatic number of a digraph’, J. Combin. Theory B 33 (1982), 265–270.Google Scholar
Neumann-Lara, V., ‘The 3 and 4-dichromatic tournaments of minimum order’, Discrete Math. 135 (1994), 233–243.CrossRefGoogle Scholar