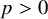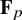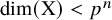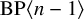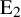Let X be a smooth and proper scheme over a perfect field k of characteristic
![]() $p>0$
. In [Reference Deligne and IllusieDI87], Deligne and Illusie proved that the Hodge decomposition holds for the de Rham cohomology of X under certain hypotheses: namely, if
$p>0$
. In [Reference Deligne and IllusieDI87], Deligne and Illusie proved that the Hodge decomposition holds for the de Rham cohomology of X under certain hypotheses: namely, if
![]() $\dim (\text{X})<p$
and X admits a smooth and proper lift to the truncated Witt vectors
$\dim (\text{X})<p$
and X admits a smooth and proper lift to the truncated Witt vectors
![]() $\text{W}_2(k) = \text{W}(k)/p^2$
, they showed that the Hodge-de Rham spectral sequence
$\text{W}_2(k) = \text{W}(k)/p^2$
, they showed that the Hodge-de Rham spectral sequence
collapses at the
![]() $\mathrm{E}_1$
-page.
$\mathrm{E}_1$
-page.
In [Reference Deligne and IllusieDI87, Remarque 2.6(iii)] (see also [Reference IllusieIll96, Problem 7.10]), Deligne and Illusie asked if the Hodge-de Rham spectral sequence could degenerate for a smooth proper k-scheme X with a lift to
![]() $\text{W}(k)/p^2$
(or even to
$\text{W}(k)/p^2$
(or even to
![]() $\text{W}(k)$
), without any dimension assumptions. This remarkable question has recently been answered (in the negative) by Sasha Petrov in [Reference PetrovPet23]. Our goal in this note is to study conditions on X arising from chromatic homotopy theory which do guarantee Hodge-de Rham degeneration if
$\text{W}(k)$
), without any dimension assumptions. This remarkable question has recently been answered (in the negative) by Sasha Petrov in [Reference PetrovPet23]. Our goal in this note is to study conditions on X arising from chromatic homotopy theory which do guarantee Hodge-de Rham degeneration if
![]() $\dim (\text{X})>p$
.
$\dim (\text{X})>p$
.
Recollection 1. Let X be a smooth scheme over a commutative ring k. One then has the HKR and de-Rham-to-
![]() $\mathrm {HP}$
spectral sequences (see [Reference Antieau, Bhatt and MathewABM21, Definition 3.1]):
$\mathrm {HP}$
spectral sequences (see [Reference Antieau, Bhatt and MathewABM21, Definition 3.1]):
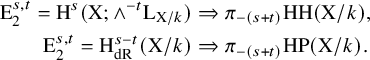 $$ \begin{align*} \mathrm{E}_2^{s,t} = {\mathrm{H}}^s(\text{X}; \wedge^{-t} \text{L}_{\text{X}/k}) & \Rightarrow \pi_{-(s+t)} \mathrm{HH}(\text{X}/k), \\ \mathrm{E}_2^{s,t} = {\mathrm{H}}^{s-t}_{\mathrm{dR}}(\text{X}/k) & \Rightarrow \pi_{-(s+t)} \mathrm{HP}(\text{X}/k). \end{align*} $$
$$ \begin{align*} \mathrm{E}_2^{s,t} = {\mathrm{H}}^s(\text{X}; \wedge^{-t} \text{L}_{\text{X}/k}) & \Rightarrow \pi_{-(s+t)} \mathrm{HH}(\text{X}/k), \\ \mathrm{E}_2^{s,t} = {\mathrm{H}}^{s-t}_{\mathrm{dR}}(\text{X}/k) & \Rightarrow \pi_{-(s+t)} \mathrm{HP}(\text{X}/k). \end{align*} $$
There are also the Hodge-de Rham and the Tate spectral sequences
 $$ \begin{align*} \mathrm{E}_1^{s,t} = {\mathrm{H}}^s(\text{X}; \wedge^{t} \text{L}_{\text{X}/k}) & \Rightarrow {\mathrm{H}}^{s+t}_{\mathrm{dR}}(\text{X}/k), \\ \mathrm{E}_2^{s,t} = \hat{{\mathrm{H}}}^s(\mathrm{BS}^1; \pi_t \mathrm{HH}(\mathcal{C}/\mathbf{F}_p)) & \Rightarrow \pi_{t-s} \mathrm{HP}(\mathcal{C}/\mathbf{F}_p), \end{align*} $$
$$ \begin{align*} \mathrm{E}_1^{s,t} = {\mathrm{H}}^s(\text{X}; \wedge^{t} \text{L}_{\text{X}/k}) & \Rightarrow {\mathrm{H}}^{s+t}_{\mathrm{dR}}(\text{X}/k), \\ \mathrm{E}_2^{s,t} = \hat{{\mathrm{H}}}^s(\mathrm{BS}^1; \pi_t \mathrm{HH}(\mathcal{C}/\mathbf{F}_p)) & \Rightarrow \pi_{t-s} \mathrm{HP}(\mathcal{C}/\mathbf{F}_p), \end{align*} $$
where
![]() $\hat {{\mathrm {H}}}$
denotes Tate cohomology. Note that if we write
$\hat {{\mathrm {H}}}$
denotes Tate cohomology. Note that if we write
![]() ${\mathrm {H}}^\ast (\mathrm{BS}^1; \mathbf {F}_p) = \mathbf {F}_p[\hbar ]$
with
${\mathrm {H}}^\ast (\mathrm{BS}^1; \mathbf {F}_p) = \mathbf {F}_p[\hbar ]$
with
![]() $\hbar $
in cohomological degree
$\hbar $
in cohomological degree
![]() $2$
, then the
$2$
, then the
![]() $\mathrm{E}_2$
-page of the Tate spectral sequence can be rewritten as
$\mathrm{E}_2$
-page of the Tate spectral sequence can be rewritten as
![]() $\pi _\ast \mathrm {HH}(\mathcal {C}/\mathbf {F}_p)[\hbar ^{\pm 1}]$
.
$\pi _\ast \mathrm {HH}(\mathcal {C}/\mathbf {F}_p)[\hbar ^{\pm 1}]$
.
Let
![]() $n \leq \infty $
. Fix an
$n \leq \infty $
. Fix an
![]() ${\mathbf {E}_{{3}}}$
-form of the (p-completed) truncated Brown-Peterson spectrum
${\mathbf {E}_{{3}}}$
-form of the (p-completed) truncated Brown-Peterson spectrum
![]() $\mathrm {BP}\langle {n-1}\rangle $
of height
$\mathrm {BP}\langle {n-1}\rangle $
of height
![]() $n-1$
, which exists thanks to [Reference Hahn and WilsonHW20, Theorem A]. By construction,
$n-1$
, which exists thanks to [Reference Hahn and WilsonHW20, Theorem A]. By construction,
![]() $\pi _\ast \mathrm {BP}\langle {n-1}\rangle \cong \mathbf {Z}_p[v_1, \cdots , v_{n-1}]$
for classes
$\pi _\ast \mathrm {BP}\langle {n-1}\rangle \cong \mathbf {Z}_p[v_1, \cdots , v_{n-1}]$
for classes
![]() $v_i$
in degree
$v_i$
in degree
![]() $2p^i-2$
. By convention,
$2p^i-2$
. By convention,
![]() $\mathrm {BP}\langle {-1}\rangle = \mathbf {F}_p$
. We also have
$\mathrm {BP}\langle {-1}\rangle = \mathbf {F}_p$
. We also have
![]() $\mathrm {BP}\langle {0}\rangle = \mathbf {Z}_p$
, and
$\mathrm {BP}\langle {0}\rangle = \mathbf {Z}_p$
, and
![]() $\mathrm {BP}\langle {1}\rangle $
can be identified with the connective cover of the Adams summand of p-completed complex K-theory. There is also a tight relationship between
$\mathrm {BP}\langle {1}\rangle $
can be identified with the connective cover of the Adams summand of p-completed complex K-theory. There is also a tight relationship between
![]() $\mathrm {BP}\langle {2}\rangle $
and elliptic cohomology. When
$\mathrm {BP}\langle {2}\rangle $
and elliptic cohomology. When
![]() $n = \infty $
, the
$n = \infty $
, the
![]() ${\mathbf {E}_{{3}}}$
-ring
${\mathbf {E}_{{3}}}$
-ring
![]() $\mathrm {BP}\langle {\infty }\rangle $
is denoted
$\mathrm {BP}\langle {\infty }\rangle $
is denoted
![]() $\mathrm {BP}$
, and is called the Brown-Peterson spectrum.
$\mathrm {BP}$
, and is called the Brown-Peterson spectrum.
Our goal in this note is to prove the following:
Theorem 2. Let
![]() $n \leq \infty $
, and let X be a smooth and proper scheme overFootnote
1
$n \leq \infty $
, and let X be a smooth and proper scheme overFootnote
1
![]() $\mathbf {F}_p$
of dimension
$\mathbf {F}_p$
of dimension
![]() $<p^n$
. Suppose that
$<p^n$
. Suppose that
-
a. The HKR spectral sequence degenerates at the
 $\mathrm{E}_2$
-page; and
$\mathrm{E}_2$
-page; and -
b.
 $\operatorname {{\mathrm {QCoh}}}(\text{X})$
lifts to a smooth and proper left
$\operatorname {{\mathrm {QCoh}}}(\text{X})$
lifts to a smooth and proper left
 $\mathrm {BP}\langle {n-1}\rangle $
-linear
$\mathrm {BP}\langle {n-1}\rangle $
-linear
 $\infty $
-category.Footnote
2
$\infty $
-category.Footnote
2
Then the Hodge-de Rham spectral sequence
collapses at the
![]() $\mathrm{E}_1$
-page, and the de-Rham-to-
$\mathrm{E}_1$
-page, and the de-Rham-to-
![]() $\mathrm {HP}$
spectral sequence collapses at the
$\mathrm {HP}$
spectral sequence collapses at the
![]() $\mathrm{E}_2$
-page.
$\mathrm{E}_2$
-page.
The discussion in [Reference Antieau, Bhatt and MathewABM21, Remark 3.6] implies that if the HKR and Tate spectral sequences both degenerate, then both the Hodge-de Rham and de Rham-to-
![]() $\mathrm {HP}$
spectral sequences must also degenerate. It therefore suffices to prove the following noncommutative statementFootnote
3
:
$\mathrm {HP}$
spectral sequences must also degenerate. It therefore suffices to prove the following noncommutative statementFootnote
3
:
Proposition 3. Let
![]() $n\leq \infty $
, and let
$n\leq \infty $
, and let
![]() $\mathcal {C}$
be a smooth and proper
$\mathcal {C}$
be a smooth and proper
![]() $\mathbf {F}_p$
-linear
$\mathbf {F}_p$
-linear
![]() $\infty $
-category such that
$\infty $
-category such that
![]() $\pi _j \mathrm {HH}(\mathcal {C}/\mathbf {F}_p) = 0$
for
$\pi _j \mathrm {HH}(\mathcal {C}/\mathbf {F}_p) = 0$
for
![]() $j\not \in [-p^n,p^n]$
. If
$j\not \in [-p^n,p^n]$
. If
![]() $\mathcal {C}$
lifts to a smooth and proper left
$\mathcal {C}$
lifts to a smooth and proper left
![]() $\mathrm {BP}\langle {n-1}\rangle $
-linear
$\mathrm {BP}\langle {n-1}\rangle $
-linear
![]() $\infty $
-category, then the Tate spectral sequence
$\infty $
-category, then the Tate spectral sequence
collapses at the
![]() $\mathrm{E}_2$
-page.
$\mathrm{E}_2$
-page.
Remark 4. When
![]() $n=1$
, Theorem 2 is part of the main result of [Reference Deligne and IllusieDI87]Footnote
4
: in this case, condition (b) in Theorem 2 is asking for a lifting to
$n=1$
, Theorem 2 is part of the main result of [Reference Deligne and IllusieDI87]Footnote
4
: in this case, condition (b) in Theorem 2 is asking for a lifting to
![]() $\mathrm {BP}\langle {0}\rangle = \mathbf {Z}_p$
. As mentioned above, Sasha Petrov recently constructed in [Reference PetrovPet23] a
$\mathrm {BP}\langle {0}\rangle = \mathbf {Z}_p$
. As mentioned above, Sasha Petrov recently constructed in [Reference PetrovPet23] a
![]() $(p+1)$
-dimensional smooth and proper
$(p+1)$
-dimensional smooth and proper
![]() $\mathbf {Z}_p$
-scheme
$\mathbf {Z}_p$
-scheme
![]() $\mathfrak {X}$
such that the Hodge-de Rham spectral sequence for its special fiber
$\mathfrak {X}$
such that the Hodge-de Rham spectral sequence for its special fiber
![]() $\mathfrak {X}_{p=0}$
does not degenerate at the
$\mathfrak {X}_{p=0}$
does not degenerate at the
![]() $\mathrm{E}_1$
-page. If the HKR spectral sequence degenerates at the
$\mathrm{E}_1$
-page. If the HKR spectral sequence degenerates at the
![]() $\mathrm{E}_2$
-page for Petrov’s
$\mathrm{E}_2$
-page for Petrov’s
![]() $\mathfrak {X}_{p=0}$
, then
$\mathfrak {X}_{p=0}$
, then
![]() $\operatorname {{\mathrm {QCoh}}}(\mathfrak {X})$
provides an example of a
$\operatorname {{\mathrm {QCoh}}}(\mathfrak {X})$
provides an example of a
![]() $\mathbf {Z}_p$
-linear
$\mathbf {Z}_p$
-linear
![]() $\infty $
-category which cannot lift to a
$\infty $
-category which cannot lift to a
![]() $\mathrm {ku}$
-linear
$\mathrm {ku}$
-linear
![]() $\infty $
-category.
$\infty $
-category.
We view Theorem 2 as a step towards a positive answer of Deligne and Illusie’s question in some generality. Note that condition (b) in Theorem 2 is significantly weaker than asking that X itself admit some sort of lifting as a spectral scheme. Note, also, that we do not prove anything nearly as refined as [Reference Deligne and IllusieDI87]: namely, we do not provide any sort of correspondence between liftings and splittings of truncations of the de Rham complex. For instance, it would be very interesting if, for a
![]() $\mathbf {Z}_p$
-scheme
$\mathbf {Z}_p$
-scheme
![]() $\mathfrak {X}$
, there were a relationship between splittings of the mod p reduction
$\mathfrak {X}$
, there were a relationship between splittings of the mod p reduction ![]() of the zeroth generalized eigenspace of the diffracted Hodge complex (see [Reference Bhatt and LurieBL22a, Remark 4.7.20] for this notion) and liftings of
of the zeroth generalized eigenspace of the diffracted Hodge complex (see [Reference Bhatt and LurieBL22a, Remark 4.7.20] for this notion) and liftings of
![]() $\operatorname {{\mathrm {QCoh}}}(\mathfrak {X})$
to
$\operatorname {{\mathrm {QCoh}}}(\mathfrak {X})$
to
![]() $\mathrm {BP}\langle {1}\rangle $
.
$\mathrm {BP}\langle {1}\rangle $
.
Remark 5. Let
![]() $\text{I} = (p^2, v_1^2, \cdots , v_{n-1}^2)$
. If
$\text{I} = (p^2, v_1^2, \cdots , v_{n-1}^2)$
. If
![]() $\mathrm {BP}\langle {n-1}\rangle /\text{I}$
were to admit the structure of an
$\mathrm {BP}\langle {n-1}\rangle /\text{I}$
were to admit the structure of an
![]() ${\mathbf {E}_{{2}}}$
-ring, Theorem 2 (and Proposition 3) would continue to hold with
${\mathbf {E}_{{2}}}$
-ring, Theorem 2 (and Proposition 3) would continue to hold with
![]() $\mathrm {BP}\langle {n-1}\rangle $
replaced by
$\mathrm {BP}\langle {n-1}\rangle $
replaced by
![]() $\mathrm {BP}\langle {n-1}\rangle /\text{I}$
. This is because one can prove that Lemma 10 continues to hold for
$\mathrm {BP}\langle {n-1}\rangle /\text{I}$
. This is because one can prove that Lemma 10 continues to hold for
![]() $\mathrm {BP}\langle {n-1}\rangle /\text{I}$
.
$\mathrm {BP}\langle {n-1}\rangle /\text{I}$
.
Some preliminary calculations seem to suggest that Petrov’s first Sen class (see [Reference PetrovPet23, Reference IllusieIll22]) is related to the obstruction in Hochschild cohomology to lifting a
![]() $\mathbf {Z}_p$
-scheme
$\mathbf {Z}_p$
-scheme
![]() $\mathfrak {X}$
along the map
$\mathfrak {X}$
along the map
![]() $\mathrm {BP}\langle {1}\rangle /v_1^2 \to \mathbf {Z}_p$
(and even along the map
$\mathrm {BP}\langle {1}\rangle /v_1^2 \to \mathbf {Z}_p$
(and even along the map
![]() $\tau _{\leq 2p-3} j \to \mathbf {Z}_p$
, where j is the connective complex image-of-J spectrum). For instance, the first k-invariant of
$\tau _{\leq 2p-3} j \to \mathbf {Z}_p$
, where j is the connective complex image-of-J spectrum). For instance, the first k-invariant of
![]() $\mathrm {BP}\langle {1}\rangle /v_1^2$
is given by the map
$\mathrm {BP}\langle {1}\rangle /v_1^2$
is given by the map
![]() $\mathbf {Z}_p \to \mathbf {Z}_p[2p-1]$
defined via the composite
$\mathbf {Z}_p \to \mathbf {Z}_p[2p-1]$
defined via the composite
where
![]() $\text{P}^1$
is a Steenrod operation and
$\text{P}^1$
is a Steenrod operation and
![]() $\beta $
is the Bockstein. In other words,
$\beta $
is the Bockstein. In other words,
![]() $\mathrm {BP}\langle {1}\rangle /v_1^2$
is equivalent to the fiber of the above composite. However, the extension class for
$\mathrm {BP}\langle {1}\rangle /v_1^2$
is equivalent to the fiber of the above composite. However, the extension class for ![]() is computed in [Reference PetrovPet23, Lemma 6.5] to be the composite
is computed in [Reference PetrovPet23, Lemma 6.5] to be the composite
where the ‘first Sen class’
![]() $c_{\text{X},p}$
can be defined using Steenrod operations on cosimplicial algebras via [Reference PetrovPet23, Theorem 7.1]. We hope to explore this further to obtain a tighter connection between the results in this article and those of Petrov’s.
$c_{\text{X},p}$
can be defined using Steenrod operations on cosimplicial algebras via [Reference PetrovPet23, Theorem 7.1]. We hope to explore this further to obtain a tighter connection between the results in this article and those of Petrov’s.
Remark 6. Theorem 2 has the following counter-intuitive consequence: if the HKR spectral sequence for X degenerates at the
![]() $\mathrm{E}_2$
-page, then the differentials in the Hodge-de Rham spectral sequence obstruct the lifting of
$\mathrm{E}_2$
-page, then the differentials in the Hodge-de Rham spectral sequence obstruct the lifting of
![]() $\operatorname {{\mathrm {QCoh}}}(\text{X})$
to a smooth and proper left
$\operatorname {{\mathrm {QCoh}}}(\text{X})$
to a smooth and proper left
![]() $\mathrm {BP}\langle {n-1}\rangle $
-linear
$\mathrm {BP}\langle {n-1}\rangle $
-linear
![]() $\infty $
-category. In particular, taking
$\infty $
-category. In particular, taking
![]() $n = \infty $
, the condition in Proposition 3 that
$n = \infty $
, the condition in Proposition 3 that
![]() $\pi _j \mathrm {HH}(\mathcal {C}/\mathbf {F}_p) = 0$
for
$\pi _j \mathrm {HH}(\mathcal {C}/\mathbf {F}_p) = 0$
for
![]() $j\not \in [-p^n,p^n]$
is vacuous; so we find that if
$j\not \in [-p^n,p^n]$
is vacuous; so we find that if
![]() $\mathcal {C}$
is a smooth and proper
$\mathcal {C}$
is a smooth and proper
![]() $\mathbf {F}_p$
-linear
$\mathbf {F}_p$
-linear
![]() $\infty $
-category which admits a smooth and proper lift to
$\infty $
-category which admits a smooth and proper lift to
![]() $\mathrm {BP}$
, then its Tate spectral sequence collapses at the
$\mathrm {BP}$
, then its Tate spectral sequence collapses at the
![]() $\mathrm{E}_2$
-page.
$\mathrm{E}_2$
-page.
This was already known if
![]() $\mathcal {C}$
lifts all the way to
$\mathcal {C}$
lifts all the way to
![]() $\text{S}^0$
; see [Reference MathewMat20, Example 3.5]. In particular, therefore, one class of X for which
$\text{S}^0$
; see [Reference MathewMat20, Example 3.5]. In particular, therefore, one class of X for which
![]() $\operatorname {{\mathrm {QCoh}}}(\text{X})$
does satisfy the hypotheses of Proposition 3 and Theorem 2 are toric varieties; but in those cases, degeneration was already known for X of arbitrary dimension (since they are F-liftable). Interesting examples of Theorem 2 and Proposition 3 are currently lacking, but one would be most welcome.
$\operatorname {{\mathrm {QCoh}}}(\text{X})$
does satisfy the hypotheses of Proposition 3 and Theorem 2 are toric varieties; but in those cases, degeneration was already known for X of arbitrary dimension (since they are F-liftable). Interesting examples of Theorem 2 and Proposition 3 are currently lacking, but one would be most welcome.
Remark 7. One could also ask the following question: if
![]() $n\geq 0$
, is there an example of a smooth and proper
$n\geq 0$
, is there an example of a smooth and proper
![]() $\mathrm {BP}\langle {n-1}\rangle $
-linear
$\mathrm {BP}\langle {n-1}\rangle $
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {C}$
which does not lift to a smooth and proper left
$\mathcal {C}$
which does not lift to a smooth and proper left
![]() $\mathrm {BP}\langle {n}\rangle $
-linear
$\mathrm {BP}\langle {n}\rangle $
-linear
![]() $\infty $
-category?
$\infty $
-category?
The idea to prove Proposition 3 is essentially the argument of [Reference MathewMat20], so we recommend reading that paper first. Recall Bökstedt’s calculation that
![]() $\pi _\ast \mathrm {THH}(\mathbf {F}_p) \cong \mathbf {F}_p[\sigma ]$
, where
$\pi _\ast \mathrm {THH}(\mathbf {F}_p) \cong \mathbf {F}_p[\sigma ]$
, where
![]() $\sigma $
lives in degree
$\sigma $
lives in degree
![]() $2$
. By [Reference MathewMat20, Proposition 3.4], Proposition 3 is a consequence of the following:
$2$
. By [Reference MathewMat20, Proposition 3.4], Proposition 3 is a consequence of the following:
Proposition 8. Let
![]() $\mathcal {C}$
be a smooth and proper
$\mathcal {C}$
be a smooth and proper
![]() $\mathbf {F}_p$
-linear
$\mathbf {F}_p$
-linear
![]() $\infty $
-category such that
$\infty $
-category such that
![]() $\pi _j \mathrm {HH}(\mathcal {C}/\mathbf {F}_p) = 0$
for
$\pi _j \mathrm {HH}(\mathcal {C}/\mathbf {F}_p) = 0$
for
![]() $j\not \in [-p^n,p^n]$
. If
$j\not \in [-p^n,p^n]$
. If
![]() $\mathcal {C}$
lifts to a smooth and proper left
$\mathcal {C}$
lifts to a smooth and proper left
![]() $\mathrm {BP}\langle {n-1}\rangle $
-linear
$\mathrm {BP}\langle {n-1}\rangle $
-linear
![]() $\infty $
-category, then
$\infty $
-category, then
![]() $\mathrm {THH}(\mathcal {C})$
is
$\mathrm {THH}(\mathcal {C})$
is
![]() $\sigma $
-torsionfree.
$\sigma $
-torsionfree.
To prove Proposition 8, we need a preliminary result. It follows from [Reference Devalapurkar, Hahn, Lawson, Senger and WilsonDHL+23, Theorem 5.2 and Corollary 2.8] that there is an augmentation
![]() $\mathrm {THH}(\mathrm {BP}\langle {n-1}\rangle ) \to \mathrm {BP}\langle {n-1}\rangle $
; composing with the map
$\mathrm {THH}(\mathrm {BP}\langle {n-1}\rangle ) \to \mathrm {BP}\langle {n-1}\rangle $
; composing with the map
![]() $\mathrm {BP}\langle {n-1}\rangle \to \mathbf {F}_p$
defines a map
$\mathrm {BP}\langle {n-1}\rangle \to \mathbf {F}_p$
defines a map
![]() $\mathrm {THH}(\mathrm {BP}\langle {n-1}\rangle ) \to \mathbf {F}_p$
.
$\mathrm {THH}(\mathrm {BP}\langle {n-1}\rangle ) \to \mathbf {F}_p$
.
Proposition 9. The map
![]() $\tau _{\leq 2p^n-1} \mathrm {THH}(\mathrm {BP}\langle {n-1}\rangle ) \to \tau _{\leq 2p^n-1}\mathrm {THH}(\mathbf {F}_p)$
factors, as an
$\tau _{\leq 2p^n-1} \mathrm {THH}(\mathrm {BP}\langle {n-1}\rangle ) \to \tau _{\leq 2p^n-1}\mathrm {THH}(\mathbf {F}_p)$
factors, as an
![]() ${\mathbf {E}_{{2}}}$
-algebra map, as the composite
${\mathbf {E}_{{2}}}$
-algebra map, as the composite
Proof. It evidently suffices to show that the map
factors, as an
![]() ${\mathbf {E}_{{2}}}$
-algebra map, as the composite
${\mathbf {E}_{{2}}}$
-algebra map, as the composite
There is an
![]() ${\mathbf {E}_{{3}}}$
-map
${\mathbf {E}_{{3}}}$
-map
![]() $\mathrm {BP} \to \mathrm {BP}\langle {n}\rangle $
, which defines an
$\mathrm {BP} \to \mathrm {BP}\langle {n}\rangle $
, which defines an
![]() ${\mathbf {E}_{{2}}}$
-map
${\mathbf {E}_{{2}}}$
-map
This map is an equivalence in degrees
![]() $\leq 2p^n - 1$
.Footnote
5
Therefore, it suffices to show that the map
$\leq 2p^n - 1$
.Footnote
5
Therefore, it suffices to show that the map
![]() $\mathrm {THH}(\mathrm {BP}) \otimes _{\mathrm {BP}} \mathbf {F}_p \to \mathrm {THH}(\mathbf {F}_p)$
factors, as an
$\mathrm {THH}(\mathrm {BP}) \otimes _{\mathrm {BP}} \mathbf {F}_p \to \mathrm {THH}(\mathbf {F}_p)$
factors, as an
![]() ${\mathbf {E}_{{2}}}$
-map, as the composite
${\mathbf {E}_{{2}}}$
-map, as the composite
equivalently, that the map
![]() $\mathrm {THH}(\mathrm {BP}) \to \mathrm {THH}(\mathbf {F}_p)$
factors, as an
$\mathrm {THH}(\mathrm {BP}) \to \mathrm {THH}(\mathbf {F}_p)$
factors, as an
![]() ${\mathbf {E}_{{2}}}$
-map, as the composite
${\mathbf {E}_{{2}}}$
-map, as the composite
Here, the map
![]() $\mathrm {BP} \to \mathrm {THH}(\mathbf {F}_p)$
is just the composite of the map
$\mathrm {BP} \to \mathrm {THH}(\mathbf {F}_p)$
is just the composite of the map
![]() $\mathrm {BP} \to \mathbf {F}_p$
with the unit
$\mathrm {BP} \to \mathbf {F}_p$
with the unit
![]() $\mathbf {F}_p \to \mathrm {THH}(\mathbf {F}_p)$
. Since
$\mathbf {F}_p \to \mathrm {THH}(\mathbf {F}_p)$
. Since
![]() $\mathrm {BP}$
is an
$\mathrm {BP}$
is an
![]() ${\mathbf {E}_{{4}}}$
-algebra retract of
${\mathbf {E}_{{4}}}$
-algebra retract of
![]() $\mathrm {MU}$
(compatibly with their natural maps to
$\mathrm {MU}$
(compatibly with their natural maps to
![]() $\mathbf {F}_p$
), it suffices to replace
$\mathbf {F}_p$
), it suffices to replace
![]() $\mathrm {BP}$
by
$\mathrm {BP}$
by
![]() $\mathrm {MU}$
in the above discussion; in fact, we will even show that the map
$\mathrm {MU}$
in the above discussion; in fact, we will even show that the map
![]() $\mathrm {THH}(\mathrm {MU}) \to \mathrm {THH}(\mathbf {F}_p)$
factors, as an
$\mathrm {THH}(\mathrm {MU}) \to \mathrm {THH}(\mathbf {F}_p)$
factors, as an
![]() ${\mathbf {E}_{{3}}}$
-map, as the composite
${\mathbf {E}_{{3}}}$
-map, as the composite
Here, the map
![]() $\mathrm {MU} \to \mathrm {THH}(\mathbf {F}_p)$
is just the composite of the map
$\mathrm {MU} \to \mathrm {THH}(\mathbf {F}_p)$
is just the composite of the map
![]() $\mathrm {MU} \to \mathbf {F}_p$
with the unit
$\mathrm {MU} \to \mathbf {F}_p$
with the unit
![]() $\mathbf {F}_p \to \mathrm {THH}(\mathbf {F}_p)$
.
$\mathbf {F}_p \to \mathrm {THH}(\mathbf {F}_p)$
.
Recall from [Reference Blumberg, Cohen and SchlichtkrullBCS10] and [Reference KlangKla18] that there is an equivalence
![]() $\mathrm {THH}(\mathrm {MU}) \simeq \mathrm {MU}[\mathrm {SU}]$
of
$\mathrm {THH}(\mathrm {MU}) \simeq \mathrm {MU}[\mathrm {SU}]$
of
![]() ${\mathbf {E}_\infty }$
-
${\mathbf {E}_\infty }$
-
![]() $\mathrm {MU}$
-algebras, and that the augmentation
$\mathrm {MU}$
-algebras, and that the augmentation
![]() $\mathrm {THH}(\mathrm {MU}) \to \mathrm {MU}$
is given by taking
$\mathrm {THH}(\mathrm {MU}) \to \mathrm {MU}$
is given by taking
![]() $\mathrm {MU}$
-chains of the augmentation
$\mathrm {MU}$
-chains of the augmentation
![]() $\mathrm {SU} \to \ast $
. The
$\mathrm {SU} \to \ast $
. The
![]() ${\mathbf {E}_\infty }$
-
${\mathbf {E}_\infty }$
-
![]() $\mathrm {MU}$
-linear map
$\mathrm {MU}$
-linear map
![]() $\mathrm {THH}(\mathrm {MU}) \to \mathrm {THH}(\mathbf {F}_p)$
is therefore equivalent to the data of an
$\mathrm {THH}(\mathrm {MU}) \to \mathrm {THH}(\mathbf {F}_p)$
is therefore equivalent to the data of an
![]() ${\mathbf {E}_\infty }$
-map
${\mathbf {E}_\infty }$
-map
![]() $\mathrm {SU} \to \mathrm {GL}_1(\mathrm {THH}(\mathbf {F}_p))$
. Since
$\mathrm {SU} \to \mathrm {GL}_1(\mathrm {THH}(\mathbf {F}_p))$
. Since
![]() $\mathrm {THH}(\mathbf {F}_p)$
is concentrated in even degrees,
$\mathrm {THH}(\mathbf {F}_p)$
is concentrated in even degrees,
![]() $\mathrm {GL}_1(\mathrm {THH}(\mathbf {F}_p))$
is an
$\mathrm {GL}_1(\mathrm {THH}(\mathbf {F}_p))$
is an
![]() ${\mathbf {E}_\infty }$
-space with even homotopy. It therefore suffices to prove the following claim: any
${\mathbf {E}_\infty }$
-space with even homotopy. It therefore suffices to prove the following claim: any
![]() ${\mathbf {E}_{{3}}}$
-map
${\mathbf {E}_{{3}}}$
-map
![]() $f: \mathrm {SU} \to \text{X}$
to an
$f: \mathrm {SU} \to \text{X}$
to an
![]() ${\mathbf {E}_{{3}}}$
-space X with even homotopy factors (as an
${\mathbf {E}_{{3}}}$
-space X with even homotopy factors (as an
![]() ${\mathbf {E}_{{3}}}$
-map) through the augmentation
${\mathbf {E}_{{3}}}$
-map) through the augmentation
![]() $\mathrm {SU} \to \ast $
. Indeed, f is equivalent to the data of a map
$\mathrm {SU} \to \ast $
. Indeed, f is equivalent to the data of a map
![]() $\mathrm {B}^3 f: \mathrm {B}^3 \mathrm {SU} \to \mathrm {B}^3 \text{X}$
. Since
$\mathrm {B}^3 f: \mathrm {B}^3 \mathrm {SU} \to \mathrm {B}^3 \text{X}$
. Since
![]() $\mathrm {B}^3 \mathrm {SU} = \mathrm {BU}\langle {6}\rangle $
has an even cell decomposition and
$\mathrm {B}^3 \mathrm {SU} = \mathrm {BU}\langle {6}\rangle $
has an even cell decomposition and
![]() $\mathrm {B}^3 \text{X}$
has odd homotopy, the map
$\mathrm {B}^3 \text{X}$
has odd homotopy, the map
![]() $\mathrm {B}^3 f$
is necessarily null (so f is null as an
$\mathrm {B}^3 f$
is necessarily null (so f is null as an
![]() ${\mathbf {E}_{{3}}}$
-map), as desired.
${\mathbf {E}_{{3}}}$
-map), as desired.
The proof of the following result is a direct adaptation of that of [Reference MathewMat20, Proposition 3.7]; it could also be proved using the methods of [Reference DevalapurkarDev23].
Lemma 10. Let M be a perfect
![]() $\mathrm {THH}(\mathbf {F}_p)$
-module such that
$\mathrm {THH}(\mathbf {F}_p)$
-module such that
![]() $\pi _i(\mathrm{M}) = 0$
for
$\pi _i(\mathrm{M}) = 0$
for
![]() $i<a$
. If M lifts to a perfect
$i<a$
. If M lifts to a perfect
![]() $\mathrm {THH}(\mathrm {BP}\langle {n-1}\rangle )$
-module
$\mathrm {THH}(\mathrm {BP}\langle {n-1}\rangle )$
-module
![]() $\widetilde {\mathrm{M}}$
, then
$\widetilde {\mathrm{M}}$
, then
![]() $\sigma $
-multiplication
$\sigma $
-multiplication
![]() $\sigma : \pi _{i-2} \mathrm{M} \to \pi _i \mathrm{M}$
is injective for
$\sigma : \pi _{i-2} \mathrm{M} \to \pi _i \mathrm{M}$
is injective for
![]() $i\leq a + 2p^n-1$
.
$i\leq a + 2p^n-1$
.
Proof. To prove the result of the lemma, we can assume without loss of generality that
![]() $a=0$
. Then, there is a map
$a=0$
. Then, there is a map
which is an equivalence on
![]() $\tau _{\leq 2p^n-1}$
. By Proposition 9, the map
$\tau _{\leq 2p^n-1}$
. By Proposition 9, the map
![]() $\tau _{\leq 2p^n-1} \mathrm {THH}(\mathrm {BP}\langle {n-1}\rangle ) \to \tau _{\leq 2p^n-1}\mathrm {THH}(\mathbf {F}_p)$
factors through
$\tau _{\leq 2p^n-1} \mathrm {THH}(\mathrm {BP}\langle {n-1}\rangle ) \to \tau _{\leq 2p^n-1}\mathrm {THH}(\mathbf {F}_p)$
factors through
![]() $\mathbf {F}_p \to \tau _{\leq 2p^n-1} \mathrm {THH}(\mathbf {F}_p)$
, so we see that
$\mathbf {F}_p \to \tau _{\leq 2p^n-1} \mathrm {THH}(\mathbf {F}_p)$
, so we see that
![]() $\tau _{\leq 2p^n-1} \mathrm{M}$
is a free
$\tau _{\leq 2p^n-1} \mathrm{M}$
is a free
![]() $\tau _{\leq 2p^n-1} \mathrm {THH}(\mathbf {F}_p)$
-module on classes in nonnegative degrees. Therefore,
$\tau _{\leq 2p^n-1} \mathrm {THH}(\mathbf {F}_p)$
-module on classes in nonnegative degrees. Therefore,
![]() $\sigma $
-multiplication is injective through the stated range.
$\sigma $
-multiplication is injective through the stated range.
Proposition 8 is now a consequence of the following, whose proof is a direct adaptation of that of [Reference MathewMat20, Proposition 3.8].
Proposition 11. Let M be a perfect
![]() $\mathrm {THH}(\mathbf {F}_p)$
-module with Tor-amplitude in
$\mathrm {THH}(\mathbf {F}_p)$
-module with Tor-amplitude in
![]() $[-p^n,p^n]$
. If M lifts to a perfect
$[-p^n,p^n]$
. If M lifts to a perfect
![]() $\mathrm {THH}(\mathrm {BP}\langle {n-1}\rangle )$
-module
$\mathrm {THH}(\mathrm {BP}\langle {n-1}\rangle )$
-module
![]() $\widetilde {\mathrm{M}}$
, then M is free.
$\widetilde {\mathrm{M}}$
, then M is free.
Proof. The argument is the same as in [Reference MathewMat20, Proposition 3.8]. Indeed, M is a direct sum of
![]() $\mathrm {THH}(\mathbf {F}_p)$
-modules which are free or of the form
$\mathrm {THH}(\mathbf {F}_p)$
-modules which are free or of the form
![]() $\mathrm{M}_{i,j} = \Sigma ^i \mathrm {THH}(\mathbf {F}_p)/\sigma ^j$
(see [Reference MathewMat20, Proposition 3.3]). Since
$\mathrm{M}_{i,j} = \Sigma ^i \mathrm {THH}(\mathbf {F}_p)/\sigma ^j$
(see [Reference MathewMat20, Proposition 3.3]). Since
![]() $\mathrm{M}_{i,j}$
has Tor-amplitude in
$\mathrm{M}_{i,j}$
has Tor-amplitude in
![]() $[i,i+2j+1]$
, the condition on M implies that
$[i,i+2j+1]$
, the condition on M implies that
![]() $\mathrm{M}_{i,j}$
could appear as a summand of M if and only if
$\mathrm{M}_{i,j}$
could appear as a summand of M if and only if
![]() $-p^n\leq i \leq i+2j+1 \leq p^n$
.
$-p^n\leq i \leq i+2j+1 \leq p^n$
.
The class
![]() $\sigma ^{j-1}[i]\in \pi _{i+2j-2} \mathrm{M}_{i,j}$
is killed by
$\sigma ^{j-1}[i]\in \pi _{i+2j-2} \mathrm{M}_{i,j}$
is killed by
![]() $\sigma $
, so taking
$\sigma $
, so taking
![]() $a = -p^n$
in Lemma 10, we see that
$a = -p^n$
in Lemma 10, we see that
In particular,
![]() $i+2j+1> p^n$
, which contradicts
$i+2j+1> p^n$
, which contradicts
![]() $i+2j+1\leq p^n$
. Therefore, no
$i+2j+1\leq p^n$
. Therefore, no
![]() $\mathrm{M}_{i,j}$
can be a summand of M, so that M is free.
$\mathrm{M}_{i,j}$
can be a summand of M, so that M is free.
In the remainder of this note, we will clarify the relationship between liftings of X itself and Hodge-de Rham degeneration. First, observe that assumption (b) in Theorem 2 is only a condition on
![]() $\operatorname {{\mathrm {QCoh}}}(\text{X})$
, which is essentially whyProposition 3 is the more natural noncommutative statement. It seems to me that assumption (a) in Theorem 2 could be removed if we asked that the structure sheaf
$\operatorname {{\mathrm {QCoh}}}(\text{X})$
, which is essentially whyProposition 3 is the more natural noncommutative statement. It seems to me that assumption (a) in Theorem 2 could be removed if we asked that the structure sheaf
![]() $\mathcal {O}_{\text{X}}$
itself lifted to a sheaf of
$\mathcal {O}_{\text{X}}$
itself lifted to a sheaf of
![]() ${\mathbf {E}_{{2}}}$
-
${\mathbf {E}_{{2}}}$
-
![]() $\mathrm {BP}\langle {n-1}\rangle $
-algebras.
$\mathrm {BP}\langle {n-1}\rangle $
-algebras.
One could ask about lifting X itself as an
![]() ${\mathbf {E}_\infty }$
-spectral scheme in the current setup [Reference LurieLur17] of spectral algebraic geometry. Unfortunately, this question often does not make sense, since
${\mathbf {E}_\infty }$
-spectral scheme in the current setup [Reference LurieLur17] of spectral algebraic geometry. Unfortunately, this question often does not make sense, since
![]() $\mathrm {BP}\langle {n-1}\rangle $
is generally not an
$\mathrm {BP}\langle {n-1}\rangle $
is generally not an
![]() ${\mathbf {E}_\infty }$
-ring [Reference LawsonLaw18, Reference SengerSen17]. Nevertheless, the question does make sense if, for instance,
${\mathbf {E}_\infty }$
-ring [Reference LawsonLaw18, Reference SengerSen17]. Nevertheless, the question does make sense if, for instance,
![]() $n=2$
(since
$n=2$
(since
![]() $\mathrm {BP}\langle {1}\rangle $
is an
$\mathrm {BP}\langle {1}\rangle $
is an
![]() ${\mathbf {E}_\infty }$
-ring). In this case, requiring that X lift is significantly stronger than the assumptions of Theorem 2, as shown by the following.
${\mathbf {E}_\infty }$
-ring). In this case, requiring that X lift is significantly stronger than the assumptions of Theorem 2, as shown by the following.
Proposition 12. Let X be a smooth and proper
![]() $\mathbf {F}_p$
-scheme. If X lifts to a p-adic flat
$\mathbf {F}_p$
-scheme. If X lifts to a p-adic flat
![]() $\mathrm {ku}^\wedge _p$
-scheme
$\mathrm {ku}^\wedge _p$
-scheme
![]() $\mathfrak {X}$
, then the Hodge-de Rham spectral sequence for X degenerates at the
$\mathfrak {X}$
, then the Hodge-de Rham spectral sequence for X degenerates at the
![]() $\mathrm{E}_1$
-page.
$\mathrm{E}_1$
-page.
Proof. The lift
![]() $\mathfrak {X}$
defines a lift of X to
$\mathfrak {X}$
defines a lift of X to
![]() $\mathbf {Z}_p$
via
$\mathbf {Z}_p$
via
![]() $\mathfrak {X}_0 := \mathfrak {X} \otimes _{\mathrm {ku}^\wedge _p} \mathbf {Z}_p$
. It suffices to show that
$\mathfrak {X}_0 := \mathfrak {X} \otimes _{\mathrm {ku}^\wedge _p} \mathbf {Z}_p$
. It suffices to show that
![]() $\mathfrak {X}_0$
admits a
$\mathfrak {X}_0$
admits a
![]() $\delta $
-ring structure; then, the Hodge-Tate gerbe over
$\delta $
-ring structure; then, the Hodge-Tate gerbe over
![]() $\mathfrak {X}_0$
(from [Reference Bhatt and LurieBL22b, Proposition 5.12]) splits, so that the conjugate (and hence Hodge-de Rham) spectral sequence for X degenerates. The fact that
$\mathfrak {X}_0$
(from [Reference Bhatt and LurieBL22b, Proposition 5.12]) splits, so that the conjugate (and hence Hodge-de Rham) spectral sequence for X degenerates. The fact that
![]() $\mathfrak {X}$
is assumed to be flat implies that
$\mathfrak {X}$
is assumed to be flat implies that
![]() $\pi _0 \text{L}_{\text{K}(1)} \mathcal {O}_{\mathfrak {X}} \cong \pi _0 \mathcal {O}_{\mathfrak {X}} = \mathcal {O}_{\mathfrak {X}_0}$
. By [Reference HopkinsHop14], if R is any
$\pi _0 \text{L}_{\text{K}(1)} \mathcal {O}_{\mathfrak {X}} \cong \pi _0 \mathcal {O}_{\mathfrak {X}} = \mathcal {O}_{\mathfrak {X}_0}$
. By [Reference HopkinsHop14], if R is any
![]() $\text{K}(1)$
-local
$\text{K}(1)$
-local
![]() ${\mathbf {E}_\infty }$
-ring, then
${\mathbf {E}_\infty }$
-ring, then
![]() $\pi _0(\text{R})$
admits a
$\pi _0(\text{R})$
admits a
![]() $\delta $
-ring structure (functorially in R). Globalizing, we see that
$\delta $
-ring structure (functorially in R). Globalizing, we see that
![]() $\pi _0 \text{L}_{\text{K}(1)} \mathcal {O}_{\mathfrak {X}} = \mathcal {O}_{\mathfrak {X}_0}$
has a
$\pi _0 \text{L}_{\text{K}(1)} \mathcal {O}_{\mathfrak {X}} = \mathcal {O}_{\mathfrak {X}_0}$
has a
![]() $\delta $
-ring structure, which implies the desired claim.
$\delta $
-ring structure, which implies the desired claim.
Remark 13. It follows from Proposition 12 that lifting an arbitrary-dimensional X to a
![]() $\mathrm {ku}^\wedge _p$
-scheme suffices to conclude Hodge-de Rham degeneration; in particular, this assumption is significantly stronger than those of Theorem 2. One intermediate between the assumptions of Proposition 12 and Theorem 2 is the following: one could assume that
$\mathrm {ku}^\wedge _p$
-scheme suffices to conclude Hodge-de Rham degeneration; in particular, this assumption is significantly stronger than those of Theorem 2. One intermediate between the assumptions of Proposition 12 and Theorem 2 is the following: one could assume that
![]() $\mathcal {O}_{\text{X}}$
only admit a lift to a sheaf of
$\mathcal {O}_{\text{X}}$
only admit a lift to a sheaf of
![]() ${\mathbf {E}_{{m}}}$
-
${\mathbf {E}_{{m}}}$
-
![]() $\mathrm {BP}\langle {n-1}\rangle $
-algebras (whenever this makes sense). Proposition 12 corresponds to the case
$\mathrm {BP}\langle {n-1}\rangle $
-algebras (whenever this makes sense). Proposition 12 corresponds to the case
![]() $n=2$
and
$n=2$
and
![]() $m=\infty $
, while Theorem 2 roughly corresponds to the case
$m=\infty $
, while Theorem 2 roughly corresponds to the case
![]() $m=1$
(and n arbitrary). What constraints does such a lifting impose on the Hodge-de Rham spectral sequence for X? For instance, if p is an odd prime, and
$m=1$
(and n arbitrary). What constraints does such a lifting impose on the Hodge-de Rham spectral sequence for X? For instance, if p is an odd prime, and
![]() $\mathcal {O}_{\text{X}}$
admits a flat lift to a sheaf of
$\mathcal {O}_{\text{X}}$
admits a flat lift to a sheaf of
![]() ${\mathbf {E}_{{2n+1}}}$
-
${\mathbf {E}_{{2n+1}}}$
-
![]() $\mathrm {ku}^\wedge _p$
-algebras, then the general construction of power operations (following [Reference HopkinsHop14]) along with the equivalence
$\mathrm {ku}^\wedge _p$
-algebras, then the general construction of power operations (following [Reference HopkinsHop14]) along with the equivalence
![]() $\text{L}_{\text{K}(1)} \mathrm {Conf}^{\mathrm {un}}_p(\mathbf {R}^{2n+1}) \simeq \text{L}_{\text{K}(1)} \text{S}^{-1}/p^n$
of [Reference DavisDav86] shows that
$\text{L}_{\text{K}(1)} \mathrm {Conf}^{\mathrm {un}}_p(\mathbf {R}^{2n+1}) \simeq \text{L}_{\text{K}(1)} \text{S}^{-1}/p^n$
of [Reference DavisDav86] shows that
![]() $\mathfrak {X}_0$
has a lift of Frobenius modulo
$\mathfrak {X}_0$
has a lift of Frobenius modulo
![]() $p^{n+1}$
. In particular, if
$p^{n+1}$
. In particular, if
![]() $\mathcal {O}_{\text{X}}$
admits a flat lift to a sheaf of
$\mathcal {O}_{\text{X}}$
admits a flat lift to a sheaf of
![]() ${\mathbf {E}_{{3}}}$
-
${\mathbf {E}_{{3}}}$
-
![]() $\mathrm {ku}^\wedge _p$
-algebras, and
$\mathrm {ku}^\wedge _p$
-algebras, and
![]() $\dim (\text{X})<p$
, then [Reference Deligne and IllusieDI87] implies that the Hodge-de Rham spectral sequence degenerates for X.
$\dim (\text{X})<p$
, then [Reference Deligne and IllusieDI87] implies that the Hodge-de Rham spectral sequence degenerates for X.
Remark 14. Finally, one might wonder whether a lifting of X to
![]() $\mathrm {BP}\langle {n-1}\rangle $
, or
$\mathrm {BP}\langle {n-1}\rangle $
, or
![]() $\mathrm {ku}^\wedge _p$
, or even the sphere spectrum can be used to prove that the HKR spectral sequence degenerates. Unfortunately, it seems that there is no clear relationship between HKR degeneration and liftings to the sphere. For instance, the stack
$\mathrm {ku}^\wedge _p$
, or even the sphere spectrum can be used to prove that the HKR spectral sequence degenerates. Unfortunately, it seems that there is no clear relationship between HKR degeneration and liftings to the sphere. For instance, the stack
![]() $\text{B}\mu _p$
over
$\text{B}\mu _p$
over
![]() $\mathbf {Z}_p$
lifts to the p-complete sphere spectrum (by writing
$\mathbf {Z}_p$
lifts to the p-complete sphere spectrum (by writing
![]() $\mu _p = \operatorname {\mathrm {Spec}} \text{S}[\mathbf {Z}/p]$
), but the HKR spectral sequence for
$\mu _p = \operatorname {\mathrm {Spec}} \text{S}[\mathbf {Z}/p]$
), but the HKR spectral sequence for
![]() $\text{B}\mu _p$
does not degenerate by [Reference Antieau, Bhatt and MathewABM21, Theorem 4.6]. Nevertheless, there are some liftability and torsion-freeness criteria, such as those described by Antieau-Vezzosi in [Reference Antieau and VezzosiAV20, Remark 1.6 and Example 1.7], which do guarantee HKR degeneration.
$\text{B}\mu _p$
does not degenerate by [Reference Antieau, Bhatt and MathewABM21, Theorem 4.6]. Nevertheless, there are some liftability and torsion-freeness criteria, such as those described by Antieau-Vezzosi in [Reference Antieau and VezzosiAV20, Remark 1.6 and Example 1.7], which do guarantee HKR degeneration.
Competing interest
The author has no competing interests to declare.
Financial support
Part of this work was done when the author was supported by the PD Soros Fellowship and NSF DGE-2140743. I am grateful to Ben Antieau, Bhargav Bhatt, Jeremy Hahn and the referee for suggestions which improved this note.