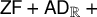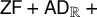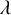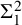1 Introduction
Universal Baireness has come to be seen in modern set theory as a sort of master regularity property for sets of real numbers, implying for instance both Lebesgue measurability and the property of Baire. Moreover, assuming the existence of suitable large cardinals, it is a property shared by every set of reals with a sufficiently simple definition. For instance, if there exist proper class many Woodin cardinals, then every set of reals in the inner model
![]() $L(\mathbb {R})$
(the smallest transitive model of
$L(\mathbb {R})$
(the smallest transitive model of
![]() $\mathsf {ZF}$
containing the reals and the ordinals) is universally Baire in the full universe V (see, for instance, Theorems 3.3.9 and 3.3.13 of [Reference Larson10]). In this case,
$\mathsf {ZF}$
containing the reals and the ordinals) is universally Baire in the full universe V (see, for instance, Theorems 3.3.9 and 3.3.13 of [Reference Larson10]). In this case,
![]() $L(\mathbb {R})$
also satisfies the Axiom of Determinacy (
$L(\mathbb {R})$
also satisfies the Axiom of Determinacy (
![]() $\mathsf {AD}$
). However, if
$\mathsf {AD}$
). However, if
![]() $\mathsf {AD}$
holds in
$\mathsf {AD}$
holds in
![]() $L(\mathbb {R})$
, then not every set of reals in
$L(\mathbb {R})$
, then not every set of reals in
![]() $L(\mathbb {R})$
satisfies the definition of universal Baireness in
$L(\mathbb {R})$
satisfies the definition of universal Baireness in
![]() $L(\mathbb {R})$
, since in this case,
$L(\mathbb {R})$
, since in this case,
![]() $L(\mathbb {R})$
does not satisfy the statement that every set of reals is Suslin (as defined in Definition 2.1; see, for instance, Theorems 6.24 and 6.28 of [Reference Larson11]). In this paper, we produce a model of
$L(\mathbb {R})$
does not satisfy the statement that every set of reals is Suslin (as defined in Definition 2.1; see, for instance, Theorems 6.24 and 6.28 of [Reference Larson11]). In this paper, we produce a model of
![]() $\mathsf {ZF} + \mathsf {AD}$
in which every set of reals is universally Baire. The large cardinal hypothesis used in our argument has since been shown to be optimal by Sandra Müller [Reference Müller16].
$\mathsf {ZF} + \mathsf {AD}$
in which every set of reals is universally Baire. The large cardinal hypothesis used in our argument has since been shown to be optimal by Sandra Müller [Reference Müller16].
We let
![]() $\omega $
denote the set of nonnegative integers, with the discrete topology, and we let
$\omega $
denote the set of nonnegative integers, with the discrete topology, and we let
![]() $\omega ^\omega $
denote the set of
$\omega ^\omega $
denote the set of
![]() $\omega $
-sequences from
$\omega $
-sequences from
![]() $\omega $
, with the product topology. Following set-theoretic convention, we will also denote
$\omega $
, with the product topology. Following set-theoretic convention, we will also denote
![]() $\omega ^\omega $
by
$\omega ^\omega $
by
![]() $\mathbb {R}$
and refer to its elements as reals, despite the fact that it is homeomorphic to the space of irrational numbers and not to the real line.
$\mathbb {R}$
and refer to its elements as reals, despite the fact that it is homeomorphic to the space of irrational numbers and not to the real line.
The definition of universal Baireness that we will use in this paper is the set-theoretic definition involving trees, which we postpone to Section 2. For now, we remark that every universally Baire set of reals
![]() $A \subseteq \omega ^\omega $
has the following property:
$A \subseteq \omega ^\omega $
has the following property:
-
(*) For every topological space X with a regular open base and every continuous function
 $f \colon X \to \omega ^\omega $
, the preimage
$f \colon X \to \omega ^\omega $
, the preimage
 $f^{-1}[A]$
has the Baire property in X.
$f^{-1}[A]$
has the Baire property in X.
Note that while every regular topological space has a regular open basis, some Hausdorff spaces do not. The property
![]() $(\ast )$
was the original definition of universal Baireness given by Feng, Magidor and Woodin in [Reference Feng, Magidor and Woodin2], where it was shown to be equivalent in
$(\ast )$
was the original definition of universal Baireness given by Feng, Magidor and Woodin in [Reference Feng, Magidor and Woodin2], where it was shown to be equivalent in
![]() $\mathsf {ZFC}$
to the definition we use in this paper [Reference Feng, Magidor and Woodin2, Corollary 2.1(3)]. We do not know if the equivalence of the two definitions follows from
$\mathsf {ZFC}$
to the definition we use in this paper [Reference Feng, Magidor and Woodin2, Corollary 2.1(3)]. We do not know if the equivalence of the two definitions follows from
![]() $\mathsf {ZF}$
, but Lemma 2.4 shows that the definition we use implies
$\mathsf {ZF}$
, but Lemma 2.4 shows that the definition we use implies
![]() $(\ast )$
, so that all sets of reals in the model we will build are universally Baire according to both definitions.
$(\ast )$
, so that all sets of reals in the model we will build are universally Baire according to both definitions.
The following is an immediate consequence of our main theorem (for which see Section 5).
Theorem 1.1. If the theory
![]() $\mathsf {ZFC} + {}$
‘there is a cardinal that is a limit of Woodin cardinals and a limit of strong cardinals’ is consistent, then so is the theory
$\mathsf {ZFC} + {}$
‘there is a cardinal that is a limit of Woodin cardinals and a limit of strong cardinals’ is consistent, then so is the theory
![]() $\mathsf {ZF} + \mathsf {AD}_{\mathbb {R}} + {}$
‘every set of reals is universally Baire’.
$\mathsf {ZF} + \mathsf {AD}_{\mathbb {R}} + {}$
‘every set of reals is universally Baire’.
The axiom
![]() $\mathsf {AD}_{\mathbb {R}}$
asserts the determinacy of all two-player games of length
$\mathsf {AD}_{\mathbb {R}}$
asserts the determinacy of all two-player games of length
![]() $\omega $
on the real numbers. The relationships between
$\omega $
on the real numbers. The relationships between
![]() $\mathsf {AD}, \ \mathsf {AD}_{\mathbb {R}}$
and
$\mathsf {AD}, \ \mathsf {AD}_{\mathbb {R}}$
and
![]() $\mathsf {AD}^{+}$
(a technical strengthening of
$\mathsf {AD}^{+}$
(a technical strengthening of
![]() $\mathsf {AD}$
whose definition we give in Section 5) are discussed in Section 5; see, for instance, [Reference Larson11] for more background.
$\mathsf {AD}$
whose definition we give in Section 5) are discussed in Section 5; see, for instance, [Reference Larson11] for more background.
Section 2 of the paper reviews universally Baire sets, and Section 3 presents some material on semiscales. The models we consider in this paper are introduced in Section 4. The main theorem of the paper is stated in Section 5, which also contains a review of symmetric extensions and homogeneously Suslin sets. The proof of the main theorem is given in Section 5, relative to three facts proved in later sections, including the
![]() $\Sigma ^{2}_{1}$
-reflection property of our model. Sections 6 (on genericity iterations) and 7 (on absoluteness) develop results needed for the proof of
$\Sigma ^{2}_{1}$
-reflection property of our model. Sections 6 (on genericity iterations) and 7 (on absoluteness) develop results needed for the proof of
![]() $\Sigma ^{2}_{1}$
reflection, which is given in Section 8. Finally, Section 9 proves a theorem of Woodin (used in the proof of the main theorem), whose proof has not previously appeared in print, and uses the machinery from this proof to fill in the last remaining detail of the proof of the main theorem.
$\Sigma ^{2}_{1}$
reflection, which is given in Section 8. Finally, Section 9 proves a theorem of Woodin (used in the proof of the main theorem), whose proof has not previously appeared in print, and uses the machinery from this proof to fill in the last remaining detail of the proof of the main theorem.
Remark 1.2. The existence of a model of
![]() $\mathsf {ZF} + \mathsf {AD}_{\mathbb {R}}$
in which all sets of reals are universally Baire was independently proved by Hugh Woodin from the stronger large cardinal hypothesis asserting the existence of proper class many Woodin limits of Woodin cardinals. From this hypothesis, he produced an inner model satisfying
$\mathsf {ZF} + \mathsf {AD}_{\mathbb {R}}$
in which all sets of reals are universally Baire was independently proved by Hugh Woodin from the stronger large cardinal hypothesis asserting the existence of proper class many Woodin limits of Woodin cardinals. From this hypothesis, he produced an inner model satisfying
![]() $\mathsf {ZF} + \mathsf {DC} + \mathsf {AD}^+ + {}$
‘
$\mathsf {ZF} + \mathsf {DC} + \mathsf {AD}^+ + {}$
‘
![]() $\omega _1$
is supercompact’, which in turn implies that every set of reals is universally Baire, and therefore that
$\omega _1$
is supercompact’, which in turn implies that every set of reals is universally Baire, and therefore that
![]() $\mathsf {AD}_{\mathbb {R}}$
holds. (In the choiceless context, supercompactness is defined in terms of normal fine measures.) Woodin’s model is an enlargement of the Chang model
$\mathsf {AD}_{\mathbb {R}}$
holds. (In the choiceless context, supercompactness is defined in terms of normal fine measures.) Woodin’s model is an enlargement of the Chang model
![]() $L(\mathrm {Ord}^\omega )$
obtained by adding a predicate for the club filter on
$L(\mathrm {Ord}^\omega )$
obtained by adding a predicate for the club filter on
![]() $\mathcal {P}_{\omega _1}(\lambda ^\omega )$
for every ordinal
$\mathcal {P}_{\omega _1}(\lambda ^\omega )$
for every ordinal
![]() $\lambda $
. Woodin showed that these predicates restrict to ultrafilters on the model. The theory
$\lambda $
. Woodin showed that these predicates restrict to ultrafilters on the model. The theory
![]() $\mathsf {ZF} + \mathsf {DC} + \mathsf {AD} + {}$
‘
$\mathsf {ZF} + \mathsf {DC} + \mathsf {AD} + {}$
‘
![]() $\omega _1$
is supercompact’ implies that the pointclass of Suslin sets of reals is closed under complementation, by a theorem of Martin and Woodin [Reference Martin and Woodin14]. Together with
$\omega _1$
is supercompact’ implies that the pointclass of Suslin sets of reals is closed under complementation, by a theorem of Martin and Woodin [Reference Martin and Woodin14]. Together with
![]() $\mathsf {AD}^+$
, this implies that every set of reals is Suslin. Using the supercompactness of
$\mathsf {AD}^+$
, this implies that every set of reals is Suslin. Using the supercompactness of
![]() $\omega _{1}$
again to take ultrapowers of trees, one can then show that every set of reals is universally Baire.
$\omega _{1}$
again to take ultrapowers of trees, one can then show that every set of reals is universally Baire.
Remark 1.3. A model of determinacy in which all sets of reals are universally Baire can be shown to exist from the theory
![]() $\mathsf {ZF}$
+
$\mathsf {ZF}$
+
![]() $\mathsf {AD}^+$
plus the assumption that there is a limit ordinal
$\mathsf {AD}^+$
plus the assumption that there is a limit ordinal
![]() $\alpha $
such that
$\alpha $
such that
![]() $\theta _\alpha $
(the
$\theta _\alpha $
(the
![]() $\alpha $
-th member of the Solovay sequence; see Section 6.3 of [Reference Larson11]) is less than
$\alpha $
-th member of the Solovay sequence; see Section 6.3 of [Reference Larson11]) is less than
![]() $\Theta $
. Assume V is a model of this theory. To construct a model of
$\Theta $
. Assume V is a model of this theory. To construct a model of
![]() $\mathsf {AD}^+$
in which all sets of reals are universally Baire, let
$\mathsf {AD}^+$
in which all sets of reals are universally Baire, let
![]() $\Delta $
be the set of reals of Wadge rank less than
$\Delta $
be the set of reals of Wadge rank less than
![]() $\theta _\alpha $
. Then
$\theta _\alpha $
. Then
![]() $M=_{\mathrm {def}}V_{\theta _{\alpha +1}}\cap \mathrm {HOD}_{\Delta }$
is a model of
$M=_{\mathrm {def}}V_{\theta _{\alpha +1}}\cap \mathrm {HOD}_{\Delta }$
is a model of
![]() $\mathsf {ZF}+ \mathsf {AD}_{\mathbb {R}}$
in which all sets of reals are universally Baire. This follows from the fact that in V, every set in
$\mathsf {ZF}+ \mathsf {AD}_{\mathbb {R}}$
in which all sets of reals are universally Baire. This follows from the fact that in V, every set in
![]() $\Delta $
is
$\Delta $
is
![]() $\kappa $
-homogenously Suslin for every
$\kappa $
-homogenously Suslin for every
![]() $\kappa <\theta _\alpha $
. We do not know if the proof of this fact has appeared in print, but it can be proven by combining the following facts: Theorem 7.5 and Lemma 7.7 of [Reference Steel23], and the results of [Reference Kechris, Kleinberg, Moschovakis and Woodin7]. See also [Reference Martin and Woodin14]. We then use Lemma 7.7 of [Reference Steel23] to conclude that M is a model of
$\kappa <\theta _\alpha $
. We do not know if the proof of this fact has appeared in print, but it can be proven by combining the following facts: Theorem 7.5 and Lemma 7.7 of [Reference Steel23], and the results of [Reference Kechris, Kleinberg, Moschovakis and Woodin7]. See also [Reference Martin and Woodin14]. We then use Lemma 7.7 of [Reference Steel23] to conclude that M is a model of
![]() $\mathsf {ZF}+ \mathsf {AD}_{\mathbb {R}}$
in which all sets of reals are universally Baire. See also Lemma 7.6 of [Reference Steel23].
$\mathsf {ZF}+ \mathsf {AD}_{\mathbb {R}}$
in which all sets of reals are universally Baire. See also Lemma 7.6 of [Reference Steel23].
We also remark that if
![]() $\theta _\alpha $
is a regular cardinal of
$\theta _\alpha $
is a regular cardinal of
![]() $\mathrm {HOD}$
, then M defined above will satisfy the theory
$\mathrm {HOD}$
, then M defined above will satisfy the theory
![]() $\mathsf {AD}_{\mathbb {R}}+`\Theta $
is a regular cardinal’ (see [Reference Caicedo, Larson, Sargsyan, Schindler, Steel and Zeman1]). By the results of [Reference Sargsyan and Trang19], in the minimal model of the Largest Suslin Axiom, there is
$\mathsf {AD}_{\mathbb {R}}+`\Theta $
is a regular cardinal’ (see [Reference Caicedo, Larson, Sargsyan, Schindler, Steel and Zeman1]). By the results of [Reference Sargsyan and Trang19], in the minimal model of the Largest Suslin Axiom, there is
![]() $\alpha $
such that
$\alpha $
such that
![]() $\theta _\alpha <\Theta $
and
$\theta _\alpha <\Theta $
and
![]() $\theta _\alpha $
is regular in
$\theta _\alpha $
is regular in
![]() $\mathrm {HOD}$
. Thus, a model of the theory
$\mathrm {HOD}$
. Thus, a model of the theory
![]() $\mathsf {AD}_{\mathbb {R}}+`\Theta $
is a regular cardinal”+“All sets of reals are universally Baire’ can be constructed inside the minimal model of the Largest Suslin Axiom.
$\mathsf {AD}_{\mathbb {R}}+`\Theta $
is a regular cardinal”+“All sets of reals are universally Baire’ can be constructed inside the minimal model of the Largest Suslin Axiom.
2 Trees, Suslin sets and universally Baire sets
In this section, we work in
![]() $\mathsf {ZF}$
, without the Axiom of Choice. A tree on a class X is a set of finite sequences
$\mathsf {ZF}$
, without the Axiom of Choice. A tree on a class X is a set of finite sequences
![]() $T \subseteq X^{\mathord {<}\omega }$
that is closed under initial segments. For such a tree, we let
$T \subseteq X^{\mathord {<}\omega }$
that is closed under initial segments. For such a tree, we let
![]() $[T]$
denote the set of all branches (infinite chains) of T, so that
$[T]$
denote the set of all branches (infinite chains) of T, so that
![]() $[T]\subseteq X^\omega $
. Note that a set
$[T]\subseteq X^\omega $
. Note that a set
![]() $A \subseteq X^\omega $
is closed in the
$A \subseteq X^\omega $
is closed in the
![]() $\omega $
-fold product of the discrete topology on X if and only if
$\omega $
-fold product of the discrete topology on X if and only if
![]() $A = \mathrm {p}[T]$
for some tree T on X. For a tree on a product
$A = \mathrm {p}[T]$
for some tree T on X. For a tree on a product
![]() $X \times Y$
, we will identify sequences of pairs with pairs of sequences (always of the same length), so for such a tree, we may write
$X \times Y$
, we will identify sequences of pairs with pairs of sequences (always of the same length), so for such a tree, we may write
![]() $[T] \subseteq X^\omega \times Y^\omega $
.
$[T] \subseteq X^\omega \times Y^\omega $
.
The trees we consider will usually be trees on the class
![]() $\omega \times \mathrm {Ord}$
where
$\omega \times \mathrm {Ord}$
where
![]() $\mathrm {Ord}$
is the class of ordinals.Footnote
1
By the projection of such a tree T, we mean the projection of
$\mathrm {Ord}$
is the class of ordinals.Footnote
1
By the projection of such a tree T, we mean the projection of
![]() $[T]$
onto its first coordinate, which is a set of reals:
$[T]$
onto its first coordinate, which is a set of reals:
An important fact that we will often use without further comment is that membership in the projection of a tree is absolute: if M is a transitive model of
![]() $\mathsf {ZF}$
containing a real x and a tree T on
$\mathsf {ZF}$
containing a real x and a tree T on
![]() $\omega \times \mathrm {Ord}$
, then
$\omega \times \mathrm {Ord}$
, then
![]() $x \in \mathrm {p}[T]$
if and only if
$x \in \mathrm {p}[T]$
if and only if
![]() $M \models x \in \mathrm {p}[T]$
. This follows from the absoluteness of wellfoundedness of the tree
$M \models x \in \mathrm {p}[T]$
. This follows from the absoluteness of wellfoundedness of the tree
![]() $T_{x} = \{t \in \mathrm {Ord}^{\mathord {<}\omega } : (x \mathord {\restriction } \left |t\right |, t) \in T\}$
. The same fact applies with V and a generic extension of V in place of M and V, respectively.
$T_{x} = \{t \in \mathrm {Ord}^{\mathord {<}\omega } : (x \mathord {\restriction } \left |t\right |, t) \in T\}$
. The same fact applies with V and a generic extension of V in place of M and V, respectively.
Definition 2.1. A set of reals A is Suslin if
![]() $A = \mathrm {p}[T]$
for some T on
$A = \mathrm {p}[T]$
for some T on
![]() $\omega \times \mathrm {Ord}$
. Given a set
$\omega \times \mathrm {Ord}$
. Given a set
![]() $X, \ A$
is X-Suslin if it is the projection of a tree on
$X, \ A$
is X-Suslin if it is the projection of a tree on
![]() $\omega \times X$
.
$\omega \times X$
.
Recall that a set of reals A is
![]() $\mathbf {\Sigma }^1_1$
(analytic) if and only if
$\mathbf {\Sigma }^1_1$
(analytic) if and only if
![]() $A = \mathrm {p}[T]$
for some T on
$A = \mathrm {p}[T]$
for some T on
![]() $\omega \times \omega $
, so the Suslin sets generalize the analytic sets.
$\omega \times \omega $
, so the Suslin sets generalize the analytic sets.
For a set
![]() $A \subseteq \omega ^\omega \times \omega ^\omega $
, we can define ‘A is Suslin’ and ‘A is
$A \subseteq \omega ^\omega \times \omega ^\omega $
, we can define ‘A is Suslin’ and ‘A is
![]() $\kappa $
-Suslin’ in terms of trees on
$\kappa $
-Suslin’ in terms of trees on
![]() $\omega \times \omega \times \mathrm {Ord}$
and
$\omega \times \omega \times \mathrm {Ord}$
and
![]() $\omega \times \omega \times \kappa $
, respectively, and similarly for
$\omega \times \omega \times \kappa $
, respectively, and similarly for
![]() $A \subseteq \omega ^\omega \times \omega ^\omega \times \omega ^\omega $
and so on. In this paper, we will typically state and prove results for sets of reals and leave the straightforward higher-dimensional generalizations to the reader.
$A \subseteq \omega ^\omega \times \omega ^\omega \times \omega ^\omega $
and so on. In this paper, we will typically state and prove results for sets of reals and leave the straightforward higher-dimensional generalizations to the reader.
Suslin sets of reals are important objects of study under the Axiom of Determinacy. Under the Axiom of Choice, however, every set of reals is Suslin (in a useless way). More generally, every wellordered set of reals
![]() $A = \{x_\alpha : \alpha < \kappa \}$
is Suslin as witnessed by the tree
$A = \{x_\alpha : \alpha < \kappa \}$
is Suslin as witnessed by the tree
on
![]() $\omega \times \kappa $
, where
$\omega \times \kappa $
, where
![]() $\bar {\alpha }$
denotes the infinite sequence with constant value
$\bar {\alpha }$
denotes the infinite sequence with constant value
![]() $\alpha $
. Universal Baireness is a strengthening of Suslinness that is nontrivial in the presence of the Axiom of Choice.
$\alpha $
. Universal Baireness is a strengthening of Suslinness that is nontrivial in the presence of the Axiom of Choice.
Instead of the original definition of universal Baireness, which we called
![]() $(\ast )$
above, we will use the following definition.
$(\ast )$
above, we will use the following definition.
Definition 2.2. Let
![]() $\mathbb {P}$
be a poset.
$\mathbb {P}$
be a poset.
-
• A pair of trees
 $(T,\tilde {T})$
on
$(T,\tilde {T})$
on
 $\omega \times \mathrm {Ord}$
is
$\omega \times \mathrm {Ord}$
is
 $\mathbb {P}$
-absolutely complementing if
$\mathbb {P}$
-absolutely complementing if
 $1_{\mathbb {P}} \mathbin {\Vdash } \mathrm {p}[T] = \omega ^\omega \setminus \mathrm {p}[\tilde {T}]$
.
$1_{\mathbb {P}} \mathbin {\Vdash } \mathrm {p}[T] = \omega ^\omega \setminus \mathrm {p}[\tilde {T}]$
. -
• A set of reals A is
 $\mathbb {P}$
-Baire if
$\mathbb {P}$
-Baire if
 $A = \mathrm {p}[T]$
for some
$A = \mathrm {p}[T]$
for some
 $\mathbb {P}$
-absolutely complementing pair of trees
$\mathbb {P}$
-absolutely complementing pair of trees
 $(T,\tilde {T})$
on
$(T,\tilde {T})$
on
 $\omega \times \mathrm {Ord}$
.
$\omega \times \mathrm {Ord}$
.
A set of reals A is universally Baire if it is
![]() $\mathbb {P}$
-Baire for every poset
$\mathbb {P}$
-Baire for every poset
![]() $\mathbb {P}$
. We write
$\mathbb {P}$
. We write
![]() $\mathrm {uB}$
for the pointclass
$\mathrm {uB}$
for the pointclass
![]() $\{A \subseteq \omega ^\omega : A \text { is universally Baire}\}$
.
$\{A \subseteq \omega ^\omega : A \text { is universally Baire}\}$
.
Remark 2.3. If a poset
![]() $\mathbb {P}$
regularly embeds into a poset
$\mathbb {P}$
regularly embeds into a poset
![]() $\mathbb {Q}$
, then every
$\mathbb {Q}$
, then every
![]() $\mathbb {Q}$
-Baire set of reals is
$\mathbb {Q}$
-Baire set of reals is
![]() $\mathbb {P}$
-Baire. A classical result of McAloon says that every partial order
$\mathbb {P}$
-Baire. A classical result of McAloon says that every partial order
![]() $\mathbb {P}$
regularly embeds into the partial order
$\mathbb {P}$
regularly embeds into the partial order
![]() $\mathrm {Col}(\omega , \mathbb {P})$
, which adds a surjection from
$\mathrm {Col}(\omega , \mathbb {P})$
, which adds a surjection from
![]() $\omega $
to
$\omega $
to
![]() $\mathbb {P}$
by finite approximations (see, for instance, the appendix to [Reference Larson10]). To show that a set of reals is universally Baire, then, it suffices to show that it is
$\mathbb {P}$
by finite approximations (see, for instance, the appendix to [Reference Larson10]). To show that a set of reals is universally Baire, then, it suffices to show that it is
![]() $\mathrm {Col}(\omega , Z)$
-Baire for every set Z. In the context of the Axiom of Choice, the set Z can be taken to be an infinite cardinal. We show in Lemma 5.7 that a similar implication holds in the models we consider in this paper.
$\mathrm {Col}(\omega , Z)$
-Baire for every set Z. In the context of the Axiom of Choice, the set Z can be taken to be an infinite cardinal. We show in Lemma 5.7 that a similar implication holds in the models we consider in this paper.
It is immediate from the definition that every universally Baire set of reals is Suslin and that the collection of universally Baire sets is closed under complements. The proof of Shoenfield’s absoluteness theorem shows that all
![]() $\mathbf {\Sigma }^1_1$
(analytic) sets of reals are universally Baire, from which it follows that all
$\mathbf {\Sigma }^1_1$
(analytic) sets of reals are universally Baire, from which it follows that all
![]() $\mathbf {\Pi }^1_1$
(coanalytic) sets are as well. Universal Baireness for more complex sets of reals is tied to large cardinals. For example, every
$\mathbf {\Pi }^1_1$
(coanalytic) sets are as well. Universal Baireness for more complex sets of reals is tied to large cardinals. For example, every
![]() $\mathbf {\Sigma }^1_2$
set of reals is universally Baire if and only if every set has a sharp, as shown by by Feng, Magidor and Woodin [Reference Feng, Magidor and Woodin2, Theorem 3.4]. As noted above, if there is a proper class of Woodin cardinals, then every set of reals in
$\mathbf {\Sigma }^1_2$
set of reals is universally Baire if and only if every set has a sharp, as shown by by Feng, Magidor and Woodin [Reference Feng, Magidor and Woodin2, Theorem 3.4]. As noted above, if there is a proper class of Woodin cardinals, then every set of reals in
![]() $L(\mathbb {R})$
is universally Baire in V.
$L(\mathbb {R})$
is universally Baire in V.
Lemma 2.4 below shows that universal Baireness implies property
![]() $(\ast )$
in
$(\ast )$
in
![]() $\mathsf {ZF}$
. We do not know whether the converse can be proved in
$\mathsf {ZF}$
. We do not know whether the converse can be proved in
![]() $\mathsf {ZF}$
. The proof uses the standard notion of the leftmost branch of a tree. That is, if S is an ill-founded tree on
$\mathsf {ZF}$
. The proof uses the standard notion of the leftmost branch of a tree. That is, if S is an ill-founded tree on
![]() $\mathrm {Ord}$
, the leftmost branch of S is the sequence
$\mathrm {Ord}$
, the leftmost branch of S is the sequence
![]() $\mathrm {lb}(S) \in \mathrm {Ord}^{\omega }$
defined recursively by letting
$\mathrm {lb}(S) \in \mathrm {Ord}^{\omega }$
defined recursively by letting
![]() $\mathrm {lb}(S)(n)$
be the least ordinal
$\mathrm {lb}(S)(n)$
be the least ordinal
![]() $\alpha $
such that the tree
$\alpha $
such that the tree
is ill-founded. Usually this operation is applied to a tree of the form
![]() $T_{x}$
(as above), where
$T_{x}$
(as above), where
![]() $x \in \omega ^{\omega }$
and T is a tree on
$x \in \omega ^{\omega }$
and T is a tree on
![]() $\omega \times \mathrm {Ord}$
, to find a witness to the statement
$\omega \times \mathrm {Ord}$
, to find a witness to the statement
![]() $x \in \mathrm {p}[T]$
.
$x \in \mathrm {p}[T]$
.
Lemma 2.4. Let
![]() $A \subseteq \omega ^\omega $
be universally Baire, let X be a topological space with a regular open base, and let
$A \subseteq \omega ^\omega $
be universally Baire, let X be a topological space with a regular open base, and let
![]() $f \colon X \to \omega ^\omega $
be a continuous function. Then the preimage
$f \colon X \to \omega ^\omega $
be a continuous function. Then the preimage
![]() $f^{-1}[A]$
has the Baire property in X.
$f^{-1}[A]$
has the Baire property in X.
Proof. The proof is a minor modification of the proof given in [Reference Feng, Magidor and Woodin2], which uses Choice for some steps. Let
![]() $\operatorname {RO}(X)$
denote the collection of all regular open subsets of X, which is a complete boolean algebra with negation given by the complement of the closure, and suprema given by the interior of the closure of the union. Considering
$\operatorname {RO}(X)$
denote the collection of all regular open subsets of X, which is a complete boolean algebra with negation given by the complement of the closure, and suprema given by the interior of the closure of the union. Considering
![]() $\mathrm {RO}(X)$
as a poset (under inclusion, with the empty set excluded), let S and T be trees witnessing that A is
$\mathrm {RO}(X)$
as a poset (under inclusion, with the empty set excluded), let S and T be trees witnessing that A is
![]() $\mathrm {RO}(X)$
-Baire, with
$\mathrm {RO}(X)$
-Baire, with
![]() $\mathrm {p}[S] = A$
. For each pair
$\mathrm {p}[S] = A$
. For each pair
![]() $n,m \in \omega $
, let
$n,m \in \omega $
, let
![]() $X_{n,m}$
be the set of
$X_{n,m}$
be the set of
![]() $x \in X$
with
$x \in X$
with
![]() $f(x)(n) = m$
. Then each
$f(x)(n) = m$
. Then each
![]() $X_{n,m}$
is in
$X_{n,m}$
is in
![]() $\mathrm {RO}(X)$
. Let
$\mathrm {RO}(X)$
. Let
![]() $\dot {g}$
be the
$\dot {g}$
be the
![]() $\operatorname {RO}(X)$
-name for an element of
$\operatorname {RO}(X)$
-name for an element of
![]() $\omega ^{\omega }$
consisting of the pairs
$\omega ^{\omega }$
consisting of the pairs
![]() $(X_{n,m}, (n,m))$
for each
$(X_{n,m}, (n,m))$
for each
![]() $n, m \in \omega $
, so that each
$n, m \in \omega $
, so that each
![]() $X_{n,m}$
forces that
$X_{n,m}$
forces that
![]() $\dot {g}(n) = m$
.
$\dot {g}(n) = m$
.
Densely many conditions in
![]() $\mathrm {RO}(X)$
decide whether the realization of
$\mathrm {RO}(X)$
decide whether the realization of
![]() $\dot {g}$
is in the projection of S or T. Let U be the union of the conditions forcing
$\dot {g}$
is in the projection of S or T. Let U be the union of the conditions forcing
![]() $\dot {g}$
into
$\dot {g}$
into
![]() $\mathrm {p}[S]$
, and let V be the corresponding set for T. Since intersections of regular open sets are regular open, U and V are disjoint. Since X has a regular open base,
$\mathrm {p}[S]$
, and let V be the corresponding set for T. Since intersections of regular open sets are regular open, U and V are disjoint. Since X has a regular open base,
![]() $U \cup V$
is dense. It suffices to see that
$U \cup V$
is dense. It suffices to see that
![]() $f^{-1}[A] \bigtriangleup U$
is meager in X.
$f^{-1}[A] \bigtriangleup U$
is meager in X.
For each
![]() $\sigma \in \omega ^{<\omega }$
, let
$\sigma \in \omega ^{<\omega }$
, let
![]() $X_{\sigma }$
be
$X_{\sigma }$
be
![]() $\bigcap _{n < |\sigma |}X_{n,\sigma (n)}$
(i.e., the set of
$\bigcap _{n < |\sigma |}X_{n,\sigma (n)}$
(i.e., the set of
![]() $x \in X$
for which
$x \in X$
for which
![]() $\sigma $
is an initial segment of
$\sigma $
is an initial segment of
![]() $f(x)$
). For each
$f(x)$
). For each
![]() $n \in \omega $
, let
$n \in \omega $
, let
![]() $\mathcal {D}_{n}$
be the set of conditions Y of
$\mathcal {D}_{n}$
be the set of conditions Y of
![]() $\mathrm {RO}(X)$
which are contained in either U or V and also in some set of the form
$\mathrm {RO}(X)$
which are contained in either U or V and also in some set of the form
![]() $X_{\sigma }$
, for some
$X_{\sigma }$
, for some
![]() $\sigma \in \omega ^{n}$
, and which decide the first n elements of the leftmost branch of whichever of
$\sigma \in \omega ^{n}$
, and which decide the first n elements of the leftmost branch of whichever of
![]() $S_{\dot {g}}$
or
$S_{\dot {g}}$
or
![]() $T_{\dot {g}}$
is ill-founded (i.e.,
$T_{\dot {g}}$
is ill-founded (i.e.,
![]() $S_{\dot {g}}$
for sets contained in U and
$S_{\dot {g}}$
for sets contained in U and
![]() $T_{\dot {g}}$
for sets contained in V). Let
$T_{\dot {g}}$
for sets contained in V). Let
![]() $\tau _{n}(Y)$
denote the length-n initial segment of this leftmost branch as decided by Y. Note then that if
$\tau _{n}(Y)$
denote the length-n initial segment of this leftmost branch as decided by Y. Note then that if
![]() $Y \in \mathcal {D}_{n}$
is contained in some such
$Y \in \mathcal {D}_{n}$
is contained in some such
![]() $X_{\sigma }$
, then the pair
$X_{\sigma }$
, then the pair
![]() $(\sigma ,\tau _{n}(Y))$
is in the corresponding tree.
$(\sigma ,\tau _{n}(Y))$
is in the corresponding tree.
For each
![]() $n \in \omega $
, let
$n \in \omega $
, let
![]() $D_{n}$
be the union of all the members of
$D_{n}$
be the union of all the members of
![]() $\mathcal {D}_{n}$
. Then each
$\mathcal {D}_{n}$
. Then each
![]() $D_{n}$
is dense open. It suffices now to see that if x is in
$D_{n}$
is dense open. It suffices now to see that if x is in
![]() $U \cap \bigcap _{n \in \omega }D_{n}$
, then
$U \cap \bigcap _{n \in \omega }D_{n}$
, then
![]() $f(x) \in A$
, and if
$f(x) \in A$
, and if
![]() $x \in V \cap \bigcap _{n \in \omega }D_{n}$
, then
$x \in V \cap \bigcap _{n \in \omega }D_{n}$
, then
![]() $f(x) \not \in A$
.
$f(x) \not \in A$
.
To see the former claim, fix
![]() $x \in U$
and regular open sets
$x \in U$
and regular open sets
![]() $Y_{n} \in \mathcal {D}_{n} (n \in \omega )$
with
$Y_{n} \in \mathcal {D}_{n} (n \in \omega )$
with
![]() $x \in \bigcap _{n \in \omega } Y_{n}$
. Each
$x \in \bigcap _{n \in \omega } Y_{n}$
. Each
![]() $Y_{n}$
is contained in some
$Y_{n}$
is contained in some
![]() $X_{\sigma _{n}}$
, in such a way that
$X_{\sigma _{n}}$
, in such a way that
![]() $f(x) = \bigcup _{n\in \omega }\sigma _{n}$
. Furthermore, since the conditions
$f(x) = \bigcup _{n\in \omega }\sigma _{n}$
. Furthermore, since the conditions
![]() $Y_{n}$
are compatible, the values
$Y_{n}$
are compatible, the values
![]() $\tau _{n}(Y_{n})$
are compatible, and the pair
$\tau _{n}(Y_{n})$
are compatible, and the pair
![]() $(f(x), \bigcup _{n \in \omega }\tau _{n}(Y_{n}))$
gives a branch through S, showing that
$(f(x), \bigcup _{n \in \omega }\tau _{n}(Y_{n}))$
gives a branch through S, showing that
![]() $f(x) \in A$
. The proof for the latter claim is the same.
$f(x) \in A$
. The proof for the latter claim is the same.
As a trivial consequence of the previous lemma, if A is universally Baire, then A itself has the Baire property. Note that if the Axiom of Choice holds, then there is a set of reals that does not have the Baire property and therefore is not universally Baire.
The following standard lemma on
![]() $\mathbb {P}$
-absolutely complementing pairs of trees is often useful.
$\mathbb {P}$
-absolutely complementing pairs of trees is often useful.
Lemma 2.5. Let T be a tree on
![]() $\omega \times \mathrm {Ord}$
, let
$\omega \times \mathrm {Ord}$
, let
![]() $\mathbb {P}$
be a poset, and let
$\mathbb {P}$
be a poset, and let
![]() $(U, \tilde {U})$
be a
$(U, \tilde {U})$
be a
![]() $\mathbb {P}$
-absolutely complementing pair of trees on
$\mathbb {P}$
-absolutely complementing pair of trees on
![]() $\omega \times \mathrm {Ord}$
. If
$\omega \times \mathrm {Ord}$
. If
![]() $\mathrm {p}[T] \subseteq \mathrm {p}[U]$
, then
$\mathrm {p}[T] \subseteq \mathrm {p}[U]$
, then
![]() $1_{\mathbb {P}} \mathbin {\Vdash } \mathrm {p}[T] \subseteq \mathrm {p}[U]$
.
$1_{\mathbb {P}} \mathbin {\Vdash } \mathrm {p}[T] \subseteq \mathrm {p}[U]$
.
Proof. If
![]() $\mathrm {p}[T] \subseteq \mathrm {p}[U]$
, then
$\mathrm {p}[T] \subseteq \mathrm {p}[U]$
, then
![]() $\mathrm {p}[T] \cap \mathrm {p}[\tilde {U}] = \emptyset $
. This implies that
$\mathrm {p}[T] \cap \mathrm {p}[\tilde {U}] = \emptyset $
. This implies that
by the absoluteness of wellfoundedness of the tree
on
![]() $\omega \times \mathrm {Ord} \times \mathrm {Ord}$
. Because
$\omega \times \mathrm {Ord} \times \mathrm {Ord}$
. Because
![]() $(U, \tilde {U})$
is
$(U, \tilde {U})$
is
![]() $\mathbb {P}$
-absolutely complementing, it follows that
$\mathbb {P}$
-absolutely complementing, it follows that
![]() $1_{\mathbb {P}} \mathbin {\Vdash } \mathrm {p}[T] \subseteq \mathrm {p}[U]$
.
$1_{\mathbb {P}} \mathbin {\Vdash } \mathrm {p}[T] \subseteq \mathrm {p}[U]$
.
Applying Lemma 2.5 in both directions, we immediately obtain the following result, which shows that although there may not be a canonical way to choose trees witnessing universal Baireness of a given set of reals, any such pair of trees gives canonical information about how to expand the set of reals in generic extensions.
Lemma 2.6. Let
![]() $\mathbb {P}$
be a poset, let A be a
$\mathbb {P}$
be a poset, let A be a
![]() $\mathbb {P}$
-Baire set of reals, and let
$\mathbb {P}$
-Baire set of reals, and let
![]() $(T,\tilde {T})$
and
$(T,\tilde {T})$
and
![]() $(U, \tilde {U})$
be
$(U, \tilde {U})$
be
![]() $\mathbb {P}$
-absolutely complementing pairs of trees witnessing that A is
$\mathbb {P}$
-absolutely complementing pairs of trees witnessing that A is
![]() $\mathbb {P}$
-Baire. Then
$\mathbb {P}$
-Baire. Then
![]() $1_{\mathbb {P}} \mathbin {\Vdash } \mathrm {p}[T] = \mathrm {p}[U]$
.
$1_{\mathbb {P}} \mathbin {\Vdash } \mathrm {p}[T] = \mathrm {p}[U]$
.
The following notation is therefore well defined.
Definition 2.7. For a poset
![]() $\mathbb {P}$
, a
$\mathbb {P}$
, a
![]() $\mathbb {P}$
-Baire set of reals A, and a V-generic filter
$\mathbb {P}$
-Baire set of reals A, and a V-generic filter
![]() $G \subseteq \mathbb {P}$
, taking any
$G \subseteq \mathbb {P}$
, taking any
![]() $\mathbb {P}$
-absolutely complementing pair of trees
$\mathbb {P}$
-absolutely complementing pair of trees
![]() $(T,\tilde {T})$
witnessing that A is
$(T,\tilde {T})$
witnessing that A is
![]() $\mathbb {P}$
-Baire, the canonical expansion of A to
$\mathbb {P}$
-Baire, the canonical expansion of A to
![]() $V[G]$
is
$V[G]$
is
Remark 2.8. The canonical expansion
![]() $A^{V[G]}$
depends only on the model
$A^{V[G]}$
depends only on the model
![]() $V[G]$
and not the generic filter G.
$V[G]$
and not the generic filter G.
We will sometimes use the following local version of universal Baireness, following Steel [Reference Steel23] and Larson [Reference Larson10].
Definition 2.9. Let
![]() $\kappa $
be a cardinal.
$\kappa $
be a cardinal.
-
• A pair of trees
 $(T,\tilde {T})$
on
$(T,\tilde {T})$
on
 $\omega \times \mathrm {Ord}$
is
$\omega \times \mathrm {Ord}$
is
 $\kappa $
-absolutely complementing if it is
$\kappa $
-absolutely complementing if it is
 $\mathbb {P}$
-absolutely complementing for every (wellordered) poset
$\mathbb {P}$
-absolutely complementing for every (wellordered) poset
 $\mathbb {P}$
of cardinality less than
$\mathbb {P}$
of cardinality less than
 $\kappa $
.
$\kappa $
. -
• A set of reals A is
 $\kappa $
-universally Baire if
$\kappa $
-universally Baire if
 $A = \mathrm {p}[T]$
for some
$A = \mathrm {p}[T]$
for some
 $\kappa $
-absolutely complementing pair of trees
$\kappa $
-absolutely complementing pair of trees
 $(T,\tilde {T})$
on
$(T,\tilde {T})$
on
 $\omega \times \mathrm {Ord}$
.
$\omega \times \mathrm {Ord}$
.
We write
![]() $\mathrm {uB}_{\kappa }$
for the pointclass
$\mathrm {uB}_{\kappa }$
for the pointclass
![]() $\{ A \subseteq \omega ^\omega : A \text { is } \kappa \text {-universally Baire}\}$
.
$\{ A \subseteq \omega ^\omega : A \text { is } \kappa \text {-universally Baire}\}$
.
The reader should be warned that because our definition says ‘cardinality less than
![]() $\kappa $
’ rather than ‘cardinality less than or equal to
$\kappa $
’ rather than ‘cardinality less than or equal to
![]() $\kappa $
’, what we call
$\kappa $
’, what we call
![]() $\kappa ^+$
-universally Baire is equivalent in
$\kappa ^+$
-universally Baire is equivalent in
![]() $\mathsf {ZFC}$
to what Feng, Magidor and Woodin call
$\mathsf {ZFC}$
to what Feng, Magidor and Woodin call
![]() $\kappa $
-universally Baire [Reference Feng, Magidor and Woodin2, Theorem 2.1].
$\kappa $
-universally Baire [Reference Feng, Magidor and Woodin2, Theorem 2.1].
One way to produce
![]() $\kappa $
-absolutely complementing trees is the Martin–Solovay construction from a system of
$\kappa $
-absolutely complementing trees is the Martin–Solovay construction from a system of
![]() $\kappa $
-complete measures (which we briefly review in Section 5; see also Section 1.3 of [Reference Larson10]). Another way, assuming the Axiom of Choice, is to amalgamate
$\kappa $
-complete measures (which we briefly review in Section 5; see also Section 1.3 of [Reference Larson10]). Another way, assuming the Axiom of Choice, is to amalgamate
![]() $\mathbb {P}$
-absolutely complementing trees for various posets
$\mathbb {P}$
-absolutely complementing trees for various posets
![]() $\mathbb {P}$
. This approach yields the following result, whose well-known proof we include here for the reader’s convenience.
$\mathbb {P}$
. This approach yields the following result, whose well-known proof we include here for the reader’s convenience.
Lemma 2.10. Assume
![]() $\mathsf {ZFC}$
, let
$\mathsf {ZFC}$
, let
![]() $\kappa $
be a cardinal, and let A be a set of reals. If A is
$\kappa $
be a cardinal, and let A be a set of reals. If A is
![]() $\mathbb {P}$
-Baire for every poset
$\mathbb {P}$
-Baire for every poset
![]() $\mathbb {P}$
of cardinality less than
$\mathbb {P}$
of cardinality less than
![]() $\kappa $
, then A is
$\kappa $
, then A is
![]() $\kappa $
-universally Baire.
$\kappa $
-universally Baire.
Proof. Let
![]() $\eta = 2^{\mathord {<}\kappa }$
and let
$\eta = 2^{\mathord {<}\kappa }$
and let
![]() $\langle \mathbb {P}_\alpha : \alpha < \eta \rangle $
enumerate the set of all posets on cardinals less than
$\langle \mathbb {P}_\alpha : \alpha < \eta \rangle $
enumerate the set of all posets on cardinals less than
![]() $\kappa $
. For each
$\kappa $
. For each
![]() $\alpha < \eta $
, choose a
$\alpha < \eta $
, choose a
![]() $\mathbb {P}_\alpha $
-absolutely complementing pair of trees
$\mathbb {P}_\alpha $
-absolutely complementing pair of trees
![]() $(T_\alpha , \tilde {T}_\alpha )$
witnessing that A is
$(T_\alpha , \tilde {T}_\alpha )$
witnessing that A is
![]() $\mathbb {P}_\alpha $
-Baire. Consider the tree T on
$\mathbb {P}_\alpha $
-Baire. Consider the tree T on
![]() $\omega \times \mathrm {Ord}$
defined by
$\omega \times \mathrm {Ord}$
defined by
This construction immediately implies that
![]() $\mathrm {p}[T] = \bigcup _{\alpha < \eta } \mathrm {p}[T_\alpha ]$
in every outer model of V. Similarly, letting
$\mathrm {p}[T] = \bigcup _{\alpha < \eta } \mathrm {p}[T_\alpha ]$
in every outer model of V. Similarly, letting
![]() $\mathrm {p}[\tilde {T}] = \bigcup _{\alpha < \eta } \mathrm {p}[\tilde {T}_\alpha ]$
in every outer model of V. In V, we have
$\mathrm {p}[\tilde {T}] = \bigcup _{\alpha < \eta } \mathrm {p}[\tilde {T}_\alpha ]$
in every outer model of V. In V, we have
![]() $\mathrm {p}[T] = A$
and
$\mathrm {p}[T] = A$
and
![]() $\mathrm {p}[\tilde {T}] = \omega ^{\omega } \setminus A$
. It follows immediately from the construction of T and
$\mathrm {p}[\tilde {T}] = \omega ^{\omega } \setminus A$
. It follows immediately from the construction of T and
![]() $\tilde {T}$
that the union of their projections is
$\tilde {T}$
that the union of their projections is
![]() $\omega ^{\omega }$
in any forcing extension by a poset of cardinality less than
$\omega ^{\omega }$
in any forcing extension by a poset of cardinality less than
![]() $\kappa $
. The absoluteness of the wellfoundedness of the tree
$\kappa $
. The absoluteness of the wellfoundedness of the tree
implies that the projections of T and
![]() $\tilde {T}$
are still disjoint in any such extension. That is, the pair
$\tilde {T}$
are still disjoint in any such extension. That is, the pair
![]() $(T, \tilde {T})$
is
$(T, \tilde {T})$
is
![]() $\kappa $
-absolutely complementing.
$\kappa $
-absolutely complementing.
It follows that, assuming the Axiom of Choice, if
![]() $\lambda $
is a limit cardinal and A is
$\lambda $
is a limit cardinal and A is
![]() $\kappa $
-universally Baire for every
$\kappa $
-universally Baire for every
![]() $\kappa < \lambda $
, then A is
$\kappa < \lambda $
, then A is
![]() $\lambda $
-universally Baire.
$\lambda $
-universally Baire.
3 Semiscales
In this section, we work in
![]() $\mathsf {ZF}$
, except where noted otherwise. A norm on a set of reals A is an ordinal-valued function on A. A prewellordering of A is a binary relation on A that is transitive and total, and whose corresponding strict relation is wellfounded. A norm
$\mathsf {ZF}$
, except where noted otherwise. A norm on a set of reals A is an ordinal-valued function on A. A prewellordering of A is a binary relation on A that is transitive and total, and whose corresponding strict relation is wellfounded. A norm
![]() $\varphi $
on a set A induces the prewellording
$\varphi $
on a set A induces the prewellording
![]() $\{ (x,y) : \varphi (x) \leq \varphi (y)\}$
, and a prewellordering
$\{ (x,y) : \varphi (x) \leq \varphi (y)\}$
, and a prewellordering
![]() $\leq $
induces the norm sending
$\leq $
induces the norm sending
![]() $x \in A$
to its
$x \in A$
to its
![]() $\leq $
-rank.
$\leq $
-rank.
Definition 3.1. Let A be a set of reals, and let
![]() $\vec {\varphi } = \langle \varphi _n : n \in \omega \rangle $
be a sequence of norms on A.
$\vec {\varphi } = \langle \varphi _n : n \in \omega \rangle $
be a sequence of norms on A.
-
1. For a sequence
 $\langle x_i : i < \omega \rangle $
of reals in A and a real y, we say that
$\langle x_i : i < \omega \rangle $
of reals in A and a real y, we say that
 $\langle x_i : i < \omega \rangle $
converges to y via
$\langle x_i : i < \omega \rangle $
converges to y via
 $\vec {\varphi }$
if x converges to y, and for every
$\vec {\varphi }$
if x converges to y, and for every
 $n < \omega $
, the sequence
$n < \omega $
, the sequence
 $\langle \varphi _n(x_i) : i < \omega \rangle $
is eventually constant.
$\langle \varphi _n(x_i) : i < \omega \rangle $
is eventually constant. -
2. We say that
 $\vec {\varphi }$
is a semiscale on A if for every sequence
$\vec {\varphi }$
is a semiscale on A if for every sequence
 $\langle x_i : i < \omega \rangle $
of reals in A and every real y, if
$\langle x_i : i < \omega \rangle $
of reals in A and every real y, if
 $\langle x_i : i < \omega \rangle $
converges to y via
$\langle x_i : i < \omega \rangle $
converges to y via
 $\vec {\varphi }$
, then
$\vec {\varphi }$
, then
 $y \in A$
.
$y \in A$
.
Remark 3.2. The condition that
![]() $\langle x_{i} : i < \omega \rangle $
converges to y via
$\langle x_{i} : i < \omega \rangle $
converges to y via
![]() $\vec {\varphi }$
in Part (2) of Definition 3.1 can equivalently be replaced with the stronger condition that
$\vec {\varphi }$
in Part (2) of Definition 3.1 can equivalently be replaced with the stronger condition that
![]() $x_{i} \mathord {\restriction } i = y \mathord {\restriction } i$
for all
$x_{i} \mathord {\restriction } i = y \mathord {\restriction } i$
for all
![]() $i < \omega $
, and
$i < \omega $
, and
![]() $\varphi _{n}(x_{i}) = \varphi _{n}(x_{j})$
whenever
$\varphi _{n}(x_{i}) = \varphi _{n}(x_{j})$
whenever
![]() $n \leq i < j$
. This can be seen by thinning a counterexample satisfying the weaker condition to produce one satisfying the stronger one.
$n \leq i < j$
. This can be seen by thinning a counterexample satisfying the weaker condition to produce one satisfying the stronger one.
If A is a Suslin set of reals, then there is a semiscale on A. More specifically, given a tree T on
![]() $\omega \times \mathrm {Ord}$
such that
$\omega \times \mathrm {Ord}$
such that
![]() $p[T] = A$
, we define the corresponding leftmost branch semiscale
$p[T] = A$
, we define the corresponding leftmost branch semiscale
![]() $\vec {\varphi }^T$
on A by letting
$\vec {\varphi }^T$
on A by letting
![]() $\varphi ^{T}_{n}(x) = \mathrm {lb}(T_{x})(n)$
. That is, for each
$\varphi ^{T}_{n}(x) = \mathrm {lb}(T_{x})(n)$
. That is, for each
![]() $n < \omega $
,
$n < \omega $
,
![]() $\varphi ^T_n(x) = \xi _n$
, where
$\varphi ^T_n(x) = \xi _n$
, where
![]() $\langle \xi _0,\ldots ,\xi _n \rangle \in \mathrm {Ord}^{n+1}$
is lexicographically least such that
$\langle \xi _0,\ldots ,\xi _n \rangle \in \mathrm {Ord}^{n+1}$
is lexicographically least such that
![]() $(x,f) \in [T]$
for some
$(x,f) \in [T]$
for some
![]() $f\in \mathrm {Ord}^\omega $
extending
$f\in \mathrm {Ord}^\omega $
extending
![]() $\langle \xi _0,\ldots ,\xi _n\rangle $
. It is straightforward to verify that this construction gives a semiscale on A.
$\langle \xi _0,\ldots ,\xi _n\rangle $
. It is straightforward to verify that this construction gives a semiscale on A.
Conversely, if there is a semiscale on A and
![]() $\mathsf {CC}_{\mathbb {R}}$
holds, then A is Suslin (
$\mathsf {CC}_{\mathbb {R}}$
holds, then A is Suslin (
![]() $\mathsf {CC}_{\mathbb {R}}$
, or countable choice for reals, is the restriction of the Axiom of Choice to countable sets of nonempty sets of real numbers; it holds in the models considered in this paper and in fact follows from
$\mathsf {CC}_{\mathbb {R}}$
, or countable choice for reals, is the restriction of the Axiom of Choice to countable sets of nonempty sets of real numbers; it holds in the models considered in this paper and in fact follows from
![]() $\mathsf {AD}$
by a theorem of Mycielski). To see this, given a semiscale
$\mathsf {AD}$
by a theorem of Mycielski). To see this, given a semiscale
![]() $\vec {\varphi }$
on A, define the tree of
$\vec {\varphi }$
on A, define the tree of
![]() $\vec {\varphi }$
by
$\vec {\varphi }$
by
Clearly,
![]() $A \subseteq \mathrm {p}[T_{\vec {\varphi }}]$
. Conversely, suppose that
$A \subseteq \mathrm {p}[T_{\vec {\varphi }}]$
. Conversely, suppose that
![]() $y \in \mathrm {p}[T_{\vec {\varphi }}]$
, and fix an
$y \in \mathrm {p}[T_{\vec {\varphi }}]$
, and fix an
![]() $f \in \mathrm {Ord}^\omega $
such that
$f \in \mathrm {Ord}^\omega $
such that
![]() $(y,f) \in [T_{\vec {\varphi }}]$
. For each
$(y,f) \in [T_{\vec {\varphi }}]$
. For each
![]() $i < \omega $
, choose a real
$i < \omega $
, choose a real
![]() $x_i$
witnessing
$x_i$
witnessing
![]() $(y \mathord {\restriction } i, f \mathord {\restriction } i) \in T_{\vec {\varphi }}$
, so that
$(y \mathord {\restriction } i, f \mathord {\restriction } i) \in T_{\vec {\varphi }}$
, so that
![]() $x_i \in A, \ y \mathord {\restriction } i = x_i \mathord {\restriction } i$
and
$x_i \in A, \ y \mathord {\restriction } i = x_i \mathord {\restriction } i$
and
![]() $f \mathord {\restriction } i = \langle \varphi _0(x_i),\ldots ,\varphi _{i-1}(x_i)\rangle $
. Then the sequence
$f \mathord {\restriction } i = \langle \varphi _0(x_i),\ldots ,\varphi _{i-1}(x_i)\rangle $
. Then the sequence
![]() $\langle x_i : i < \omega \rangle $
converges to y via
$\langle x_i : i < \omega \rangle $
converges to y via
![]() $\vec {\varphi }$
, so
$\vec {\varphi }$
, so
![]() $y \in A$
. This shows that
$y \in A$
. This shows that
![]() $A = \mathrm {p}[T_{\vec {\varphi }}]$
.
$A = \mathrm {p}[T_{\vec {\varphi }}]$
.
It follows that if
![]() $\mathsf {CC}_{\mathbb {R}}$
holds, then the Suslin sets of reals are exactly the sets of reals that admit semiscales. We do not know if this can be proved in
$\mathsf {CC}_{\mathbb {R}}$
holds, then the Suslin sets of reals are exactly the sets of reals that admit semiscales. We do not know if this can be proved in
![]() $\mathsf {ZF}$
. The following lemma can be used in some situations to show that
$\mathsf {ZF}$
. The following lemma can be used in some situations to show that
![]() $A = \mathrm {p}[T_{\vec {\varphi }}]$
without assuming
$A = \mathrm {p}[T_{\vec {\varphi }}]$
without assuming
![]() $\mathsf {CC}_{\mathbb {R}}$
. The lemma is not useful for showing that A is Suslin because that is one of the hypotheses. Rather, it is useful when we want to represent A as the projection of a tree that is definable from a given semiscale
$\mathsf {CC}_{\mathbb {R}}$
. The lemma is not useful for showing that A is Suslin because that is one of the hypotheses. Rather, it is useful when we want to represent A as the projection of a tree that is definable from a given semiscale
![]() $\vec {\varphi }$
.
$\vec {\varphi }$
.
Lemma 3.3. Let A be a set of reals, and let
![]() $\vec {\varphi }$
be a semiscale on A. Assume that the set A and the relation
$\vec {\varphi }$
be a semiscale on A. Assume that the set A and the relation
are both Suslin, where
![]() $\bar {n}$
denotes the constant function from
$\bar {n}$
denotes the constant function from
![]() $\omega $
to
$\omega $
to
![]() $\{n\}$
. Then
$\{n\}$
. Then
![]() $\mathrm {p}[T_{\vec {\varphi }}] = A$
.
$\mathrm {p}[T_{\vec {\varphi }}] = A$
.
Proof. Clearly,
![]() $A \subseteq \mathrm {p}[T_{\vec {\varphi }}]$
as before. Conversely, let
$A \subseteq \mathrm {p}[T_{\vec {\varphi }}]$
as before. Conversely, let
![]() $y \in \mathrm {p}[T_{\vec {\varphi }}]$
. Fix
$y \in \mathrm {p}[T_{\vec {\varphi }}]$
. Fix
![]() $f \in \mathrm {Ord}^\omega $
such that
$f \in \mathrm {Ord}^\omega $
such that
![]() $(y,f) \in [T_{\vec {\varphi }}]$
. Take a tree
$(y,f) \in [T_{\vec {\varphi }}]$
. Take a tree
![]() $T_A$
on
$T_A$
on
![]() $\omega \times \mathrm {Ord}$
witnessing that A is Suslin, and take a tree
$\omega \times \mathrm {Ord}$
witnessing that A is Suslin, and take a tree
![]() $T_E$
on
$T_E$
on
![]() $\omega \times \omega \times \omega \times \mathrm {Ord}$
witnessing that E is Suslin.
$\omega \times \omega \times \omega \times \mathrm {Ord}$
witnessing that E is Suslin.
For
![]() $N < \omega $
, define a full N-witness to be an object of the form
$N < \omega $
, define a full N-witness to be an object of the form
such that
-
• for all
 $i < N, \ x_i \in \omega ^\omega $
witnesses that
$i < N, \ x_i \in \omega ^\omega $
witnesses that
 $(y \mathord {\restriction } i,f \mathord {\restriction } i) \in T_{\vec {\varphi }}$
, meaning that
$(y \mathord {\restriction } i,f \mathord {\restriction } i) \in T_{\vec {\varphi }}$
, meaning that
 $x_i \in A,\ y \mathord {\restriction } i = x_i \mathord {\restriction } i$
and
$x_i \in A,\ y \mathord {\restriction } i = x_i \mathord {\restriction } i$
and
 $f \mathord {\restriction } i = \langle \varphi _0(x_i),\ldots ,\varphi _{i-1}(x_i)\rangle $
;
$f \mathord {\restriction } i = \langle \varphi _0(x_i),\ldots ,\varphi _{i-1}(x_i)\rangle $
; -
• for all
 $i < N,\ g_i \in \mathrm {Ord}^\omega $
witnesses that
$i < N,\ g_i \in \mathrm {Ord}^\omega $
witnesses that
 $x_i \in A$
in the sense that
$x_i \in A$
in the sense that
 $(x_i,g_i) \in [T_A]$
;
$(x_i,g_i) \in [T_A]$
; -
• for all
 $n \le i \le j < N, \ h_{n,i,j} \in \mathrm {Ord}^\omega $
witnesses
$n \le i \le j < N, \ h_{n,i,j} \in \mathrm {Ord}^\omega $
witnesses
 $\varphi _n(x_i) = \varphi _n(x_j)$
in the sense that
$\varphi _n(x_i) = \varphi _n(x_j)$
in the sense that
 $(\bar {n}, x_i, x_j, h_{n,i,j}) \in [T_E]$
.
$(\bar {n}, x_i, x_j, h_{n,i,j}) \in [T_E]$
.
We define a partial N-witness to be an object that can be obtained by restricting some full N-witness as above to N to produce the following:
Note that every full N-witness can be extended to a full
![]() $(N+1)$
-witness by choosing any
$(N+1)$
-witness by choosing any
![]() $x_N \in \omega ^\omega $
witnessing
$x_N \in \omega ^\omega $
witnessing
![]() $(y \mathord {\restriction } N,f \mathord {\restriction } N) \in T_{\vec {\varphi }}$
and then choosing
$(y \mathord {\restriction } N,f \mathord {\restriction } N) \in T_{\vec {\varphi }}$
and then choosing
![]() $g_N$
and
$g_N$
and
![]() $h_{n,i,N}$
appropriately for all n and i such that
$h_{n,i,N}$
appropriately for all n and i such that
![]() $n \le i \le N$
.
$n \le i \le N$
.
It follows that every partial N-witness can be extended to a partial
![]() $(N+1)$
-witness: first extend it to a full N-witness, extend that to a full
$(N+1)$
-witness: first extend it to a full N-witness, extend that to a full
![]() $(N+1)$
-witness, and then restrict that to a partial
$(N+1)$
-witness, and then restrict that to a partial
![]() $(N+1)$
-witness. By extending a partial N-witness to a partial
$(N+1)$
-witness. By extending a partial N-witness to a partial
![]() $(N+1)$
-witness, we mean that its sequences of length N are extended to sequences of length
$(N+1)$
-witness, we mean that its sequences of length N are extended to sequences of length
![]() $N+1$
, and new sequences of length
$N+1$
, and new sequences of length
![]() $N+1$
of the form
$N+1$
of the form
![]() $x_N \mathord {\restriction } (N+1),\ g_N \mathord {\restriction } (N+1)$
and
$x_N \mathord {\restriction } (N+1),\ g_N \mathord {\restriction } (N+1)$
and
![]() $h_{n,i,N} \mathord {\restriction } (N+1)$
are added.
$h_{n,i,N} \mathord {\restriction } (N+1)$
are added.
The advantage of partial witnesses (as compared with full witnesses) is that they are essentially finite sequences of ordinals, so the Axiom of Choice is not required to choose among them. We may therefore define a sequence
![]() $\langle \sigma _N : N < \omega \rangle $
where for each
$\langle \sigma _N : N < \omega \rangle $
where for each
![]() $N < \omega ,\ \sigma _N$
is an N-witness and
$N < \omega ,\ \sigma _N$
is an N-witness and
![]() $\sigma _{N+1}$
extends
$\sigma _{N+1}$
extends
![]() $\sigma _N$
. Taking
$\sigma _N$
. Taking
![]() $\bigcup _{N < \omega } \sigma _N$
, by which we really mean taking the union in each coordinate separately, we obtain an object
$\bigcup _{N < \omega } \sigma _N$
, by which we really mean taking the union in each coordinate separately, we obtain an object
Then for all
![]() $i < N$
, we have
$i < N$
, we have
![]() $x_i \in A$
as witnessed by
$x_i \in A$
as witnessed by
![]() $g_i \in \mathrm {Ord}^\omega $
. Furthermore, the sequence
$g_i \in \mathrm {Ord}^\omega $
. Furthermore, the sequence
![]() $\langle x_i : i < \omega \rangle $
converges to y since
$\langle x_i : i < \omega \rangle $
converges to y since
![]() $y \mathord {\restriction } i = x_i \mathord {\restriction } i$
for all
$y \mathord {\restriction } i = x_i \mathord {\restriction } i$
for all
![]() $i < \omega $
. We might not have
$i < \omega $
. We might not have
![]() $\varphi _n(x_i) = f(n)$
for all n and i such that
$\varphi _n(x_i) = f(n)$
for all n and i such that
![]() $n \le i < \omega $
because this property of full witnesses might be lost by passing to partial witnesses and taking unions. However, we do have
$n \le i < \omega $
because this property of full witnesses might be lost by passing to partial witnesses and taking unions. However, we do have
![]() $\varphi _n(x_i) = \varphi _n(x_j)$
for all
$\varphi _n(x_i) = \varphi _n(x_j)$
for all
![]() $n,\ i$
and j such that
$n,\ i$
and j such that
![]() $n \le i \le j < \omega $
because this is witnessed by
$n \le i \le j < \omega $
because this is witnessed by
![]() $h_{n,i,j} \in \mathrm {Ord}^\omega $
. Therefore, the sequence
$h_{n,i,j} \in \mathrm {Ord}^\omega $
. Therefore, the sequence
![]() $\langle x_i : i < \omega \rangle $
converges to y via
$\langle x_i : i < \omega \rangle $
converges to y via
![]() $\vec {\varphi }$
. Since
$\vec {\varphi }$
. Since
![]() $\vec {\varphi }$
is a semiscale on A, it follows that
$\vec {\varphi }$
is a semiscale on A, it follows that
![]() $y \in A$
, as desired.
$y \in A$
, as desired.
Let A be a set of reals and let
![]() $\vec {\varphi }$
be a semiscale on A. The canonical code for
$\vec {\varphi }$
be a semiscale on A. The canonical code for
![]() $\vec {\varphi }$
is the set R consisting of those triples
$\vec {\varphi }$
is the set R consisting of those triples
![]() $(\bar {n},x,y) \in \omega ^\omega \times A \times A$
for which
$(\bar {n},x,y) \in \omega ^\omega \times A \times A$
for which
![]() $\varphi _{n}(x) \le \varphi _{n}(y)$
, where again
$\varphi _{n}(x) \le \varphi _{n}(y)$
, where again
![]() $\bar {n}$
denotes the constant sequence
$\bar {n}$
denotes the constant sequence
![]() $(n,n,n,\ldots )$
. When this holds, we say that R codes
$(n,n,n,\ldots )$
. When this holds, we say that R codes
![]() $\vec {\varphi }$
.
$\vec {\varphi }$
.
For any ternary relation
![]() $R \subseteq \omega ^\omega \times \omega ^\omega \times \omega ^\omega $
and any
$R \subseteq \omega ^\omega \times \omega ^\omega \times \omega ^\omega $
and any
![]() $n \in \omega $
, define
$n \in \omega $
, define
Note that a set
![]() $R \subseteq \omega ^\omega \times \omega ^\omega \times \omega ^\omega $
codes a semiscale if and only if each
$R \subseteq \omega ^\omega \times \omega ^\omega \times \omega ^\omega $
codes a semiscale if and only if each
![]() $R_n$
is a prewellordering of A, and for every sequence
$R_n$
is a prewellordering of A, and for every sequence
![]() $\langle x_i : n \in \omega \rangle $
of points in A converging to a point
$\langle x_i : n \in \omega \rangle $
of points in A converging to a point
![]() $y \in \omega ^\omega $
, if for each n in
$y \in \omega ^\omega $
, if for each n in
![]() $\omega $
there is an
$\omega $
there is an
![]() $m \in \omega $
such that
$m \in \omega $
such that
![]() $x_{i}R_{n}x_{j}$
for all
$x_{i}R_{n}x_{j}$
for all
![]() $i,j \in \omega \setminus m$
, then y is in A.
$i,j \in \omega \setminus m$
, then y is in A.
The following result is immediate from the definitions.
Lemma 3.4. Let
![]() $A \subseteq \omega ^\omega $
, and let
$A \subseteq \omega ^\omega $
, and let
![]() $R \subseteq \omega ^\omega \times \omega ^\omega \times \omega ^\omega $
code a semiscale on A. Let
$R \subseteq \omega ^\omega \times \omega ^\omega \times \omega ^\omega $
code a semiscale on A. Let
![]() $\mathcal {M}$
be an inner model of
$\mathcal {M}$
be an inner model of
![]() $\mathsf {ZF}$
. If
$\mathsf {ZF}$
. If
![]() $R \cap \mathcal {M} \in \mathcal {M}$
, then
$R \cap \mathcal {M} \in \mathcal {M}$
, then
![]() $A \cap \mathcal {M} \in \mathcal {M}$
and
$A \cap \mathcal {M} \in \mathcal {M}$
and
![]() $\mathcal {M}$
satisfies ‘
$\mathcal {M}$
satisfies ‘
![]() $R \cap \mathcal {M}$
codes a semiscale on
$R \cap \mathcal {M}$
codes a semiscale on
![]() $A \cap M$
’.
$A \cap M$
’.
The following result is proved by standard arguments, but since we do not know of a reference, we include a proof here. Higher-level arguments for similar absoluteness results are given in Section 9.
Lemma 3.5. Let
![]() $A \subseteq \omega ^\omega $
, and let
$A \subseteq \omega ^\omega $
, and let
![]() $R \subseteq \omega ^\omega \times \omega ^\omega \times \omega ^\omega $
code a semiscale on A. Let
$R \subseteq \omega ^\omega \times \omega ^\omega \times \omega ^\omega $
code a semiscale on A. Let
![]() $\mathbb {P}$
be a poset, and let
$\mathbb {P}$
be a poset, and let
![]() $G\subseteq \mathbb {P}$
be a V-generic filter on
$G\subseteq \mathbb {P}$
be a V-generic filter on
![]() $\mathbb {P}$
. If A and R are
$\mathbb {P}$
. If A and R are
![]() $\mathbb {P}$
-Baire, then
$\mathbb {P}$
-Baire, then
![]() $V[G]$
satisfies ‘
$V[G]$
satisfies ‘
![]() $R^{V[G]}$
codes a semiscale on
$R^{V[G]}$
codes a semiscale on
![]() $A^{V[G]}$
’.
$A^{V[G]}$
’.
Proof. Let
![]() $(T_A, T_{\neg A})$
be a pair of trees on
$(T_A, T_{\neg A})$
be a pair of trees on
![]() $\omega \times \mathrm {Ord}$
witnessing that A is
$\omega \times \mathrm {Ord}$
witnessing that A is
![]() $\mathbb {P}$
-Baire, and let
$\mathbb {P}$
-Baire, and let
![]() $(T_R, T_{\neg R})$
be a pair of trees on
$(T_R, T_{\neg R})$
be a pair of trees on
![]() $\omega \times \omega \times \omega \times \mathrm {Ord}$
witnessing that R is
$\omega \times \omega \times \omega \times \mathrm {Ord}$
witnessing that R is
![]() $\mathbb {P}$
-Baire. The desired conclusion will follow from the fact that the wellfoundedness of various trees defined from these four trees is absolute from V to
$\mathbb {P}$
-Baire. The desired conclusion will follow from the fact that the wellfoundedness of various trees defined from these four trees is absolute from V to
![]() $V[G]$
.
$V[G]$
.
First, we show that
![]() $R^{V[G]}_n$
is a prewellordering of
$R^{V[G]}_n$
is a prewellordering of
![]() $A^{V[G]}$
for each
$A^{V[G]}$
for each
![]() $n \in \omega $
. Let
$n \in \omega $
. Let
![]() $n \in \omega $
. We have
$n \in \omega $
. We have
![]() $R_n \subseteq A \times A$
, so the trees
$R_n \subseteq A \times A$
, so the trees
and
on
![]() $\omega \times \omega \times \mathrm {Ord} \times \mathrm {Ord}$
are wellfounded, and therefore,
$\omega \times \omega \times \mathrm {Ord} \times \mathrm {Ord}$
are wellfounded, and therefore,
![]() $R^{V[G]}_n \subseteq A^{V[G]} \times A^{V[G]}$
(here,
$R^{V[G]}_n \subseteq A^{V[G]} \times A^{V[G]}$
(here,
![]() $\bar {n}$
refers to the constant sequence of length
$\bar {n}$
refers to the constant sequence of length
![]() $|s|$
with value n).
$|s|$
with value n).
Since
![]() $R_n$
is transitive, the tree on
$R_n$
is transitive, the tree on
![]() $\omega \times \omega \times \omega \times \mathrm {Ord} \times \mathrm {Ord} \times \mathrm {Ord}$
consisting of all tuples
$\omega \times \omega \times \omega \times \mathrm {Ord} \times \mathrm {Ord} \times \mathrm {Ord}$
consisting of all tuples
![]() $(s, t, u, v, w, x)$
such that
$(s, t, u, v, w, x)$
such that
-
•
 $(\bar {n}, s, t, v) \in T_{R}$
,
$(\bar {n}, s, t, v) \in T_{R}$
, -
•
 $(\bar {n}, t, u, w) \in T_{R}$
and
$(\bar {n}, t, u, w) \in T_{R}$
and -
•
 $(\bar {n}, s, u, x) \in T_{\neg R}$
$(\bar {n}, s, u, x) \in T_{\neg R}$
is wellfounded. It follows that
![]() $R^{V[G]}_n$
is transitive.
$R^{V[G]}_n$
is transitive.
Since
![]() $R_n$
is total on A, the tree on
$R_n$
is total on A, the tree on
![]() $\omega \times \omega \times \mathrm {Ord} \times \mathrm {Ord} \times \mathrm {Ord} \times \mathrm {Ord}$
consisting of all tuples
$\omega \times \omega \times \mathrm {Ord} \times \mathrm {Ord} \times \mathrm {Ord} \times \mathrm {Ord}$
consisting of all tuples
![]() $(s, t, u, v, w, x)$
such that
$(s, t, u, v, w, x)$
such that
-
•
 $(s, u) \in T_A$
$(s, u) \in T_A$
-
•
 $(t, v) \in T_A$
$(t, v) \in T_A$
-
•
 $(\bar {n}, s, t, w) \in T_{\neg R}$
, and
$(\bar {n}, s, t, w) \in T_{\neg R}$
, and -
•
 $(\bar {n}, t, s, x) \in T_{\neg R}$
$(\bar {n}, t, s, x) \in T_{\neg R}$
is wellfounded. It follows that
![]() $R^{V[G]}_n$
is total on
$R^{V[G]}_n$
is total on
![]() $A^{V[G]}$
.
$A^{V[G]}$
.
For the remaining parts, which are the wellfoundedness of each
![]() $R^{V[G]}_n$
and the semiscale condition, it will help to introduce the following notation. Fix a recursive bijection
$R^{V[G]}_n$
and the semiscale condition, it will help to introduce the following notation. Fix a recursive bijection
![]() $\omega \times \omega \to \omega $
denoted by
$\omega \times \omega \to \omega $
denoted by
![]() $(i, j) \mapsto \langle i, j \rangle $
. Given
$(i, j) \mapsto \langle i, j \rangle $
. Given
![]() $s \in \omega ^{\mathord {<}\omega }$
and integers
$s \in \omega ^{\mathord {<}\omega }$
and integers
![]() $i,j$
, define the finite sequence
$i,j$
, define the finite sequence
![]() $s_{i,j}$
to be
$s_{i,j}$
to be
![]() $\langle s(\langle i, 0\rangle ), \ldots , s(\langle i, j-1\rangle )\rangle $
if all necessary values of s are defined, and undefined otherwise.
$\langle s(\langle i, 0\rangle ), \ldots , s(\langle i, j-1\rangle )\rangle $
if all necessary values of s are defined, and undefined otherwise.
The strict part of
![]() $R_n$
is wellfounded, so
$R_n$
is wellfounded, so
![]() $R_n$
has no infinite strictly decreasing sequences. Then the tree on
$R_n$
has no infinite strictly decreasing sequences. Then the tree on
![]() $\omega \times \mathrm {Ord} \times \mathrm {Ord}$
consisting of all tuples
$\omega \times \mathrm {Ord} \times \mathrm {Ord}$
consisting of all tuples
![]() $(s, t, u)$
such that for all
$(s, t, u)$
such that for all
![]() $i,j \in \omega $
such that
$i,j \in \omega $
such that
![]() $s_{i,j}$
(and hence also
$s_{i,j}$
(and hence also
![]() $t_{i,j}$
and
$t_{i,j}$
and
![]() $u_{i,j}$
) and
$u_{i,j}$
) and
![]() $s_{i+1,j}$
are defined,
$s_{i+1,j}$
are defined,
-
•
 $(\bar {n}, s_{i+1, j}, s_{i,j}, t_{i,j}) \in T_R$
and
$(\bar {n}, s_{i+1, j}, s_{i,j}, t_{i,j}) \in T_R$
and -
•
 $(\bar {n}, s_{i,j}, s_{i+1,j}, u_{i,j}) \in T_{\neg R}$
$(\bar {n}, s_{i,j}, s_{i+1,j}, u_{i,j}) \in T_{\neg R}$
is wellfounded, so there is no strictly
![]() $R^{V[K]}_n$
-decreasing infinite sequence in any generic extension
$R^{V[K]}_n$
-decreasing infinite sequence in any generic extension
![]() $V[K]$
(we apply this fact with
$V[K]$
(we apply this fact with
![]() $K = (G,H)$
in the next paragraph).
$K = (G,H)$
in the next paragraph).
Because we are not assuming the Axiom of Choice, the previous paragraph does not immediately show that
![]() $R^{V[G]}_n$
is wellfounded. To show that it is, let S be a nonempty subset of
$R^{V[G]}_n$
is wellfounded. To show that it is, let S be a nonempty subset of
![]() $A^{V[G]}$
in
$A^{V[G]}$
in
![]() $V[G]$
. Let
$V[G]$
. Let
![]() $\mathbb {Q}$
be the poset of strictly
$\mathbb {Q}$
be the poset of strictly
![]() $R^{V[G]}_n$
-decreasing finite sequences of reals in S, ordered by reverse inclusion, and take a
$R^{V[G]}_n$
-decreasing finite sequences of reals in S, ordered by reverse inclusion, and take a
![]() $V[G]$
generic filter
$V[G]$
generic filter
![]() $H \subseteq \mathbb {Q}$
. Because the tree on
$H \subseteq \mathbb {Q}$
. Because the tree on
![]() $\omega \times \mathrm {Ord} \times \mathrm {Ord}$
defined above is still wellfounded in
$\omega \times \mathrm {Ord} \times \mathrm {Ord}$
defined above is still wellfounded in
![]() $V[G][H]$
, the sequence
$V[G][H]$
, the sequence
![]() $\bigcup H$
cannot be infinite, so it has a last element, which must be an
$\bigcup H$
cannot be infinite, so it has a last element, which must be an
![]() $R^{V[G]}_n$
-minimal element of S.
$R^{V[G]}_n$
-minimal element of S.
Lastly, we prove the semiscale condition. Because R codes a semiscale on A, the tree on
![]() $\omega \times \omega \times \mathrm {Ord} \times \mathrm {Ord} \times \mathrm {Ord}$
consisting of all tuples
$\omega \times \omega \times \mathrm {Ord} \times \mathrm {Ord} \times \mathrm {Ord}$
consisting of all tuples
![]() $(c, s, t, u, v)$
such that for all
$(c, s, t, u, v)$
such that for all
![]() $n,i,j \in \omega $
such that
$n,i,j \in \omega $
such that
![]() $c(n) \le \min (i,j)$
and
$c(n) \le \min (i,j)$
and
![]() $s_{i,j}$
(and hence also
$s_{i,j}$
(and hence also
![]() $t_{i,j}$
and
$t_{i,j}$
and
![]() $u_{i,j}$
) and
$u_{i,j}$
) and
![]() $s_{i+i,j}$
are defined,
$s_{i+i,j}$
are defined,
-
•
 $(\bar {n}, s_{i,j}, s_{i+1,j}, t_{i,j}) \in T_R$
,
$(\bar {n}, s_{i,j}, s_{i+1,j}, t_{i,j}) \in T_R$
, -
•
 $(\bar {n}, s_{i+1,j}, s_{i,j}, u_{i,j}) \in T_R$
,
$(\bar {n}, s_{i+1,j}, s_{i,j}, u_{i,j}) \in T_R$
, -
•
 $s_{i,c(n)} = s_{i+1,c(n)}$
and
$s_{i,c(n)} = s_{i+1,c(n)}$
and -
•
 $(s_{i,n}, v \mathord {\restriction } n) \in T_{\neg A}$
$(s_{i,n}, v \mathord {\restriction } n) \in T_{\neg A}$
is wellfounded (here,
![]() $c(n)$
indicates a point such that the reals
$c(n)$
indicates a point such that the reals
![]() $\bigcup _{j}s_{i,j}$
for
$\bigcup _{j}s_{i,j}$
for
![]() $i> c(n)$
agree both in the n-th norm and also for their first n digits; we could have done without c by using Remark 3.2). This, along with the fact that
$i> c(n)$
agree both in the n-th norm and also for their first n digits; we could have done without c by using Remark 3.2). This, along with the fact that
![]() $R^{V[G]}_n$
is a prewellordering of
$R^{V[G]}_n$
is a prewellordering of
![]() $A^{V[G]}$
for each
$A^{V[G]}$
for each
![]() $n \in \omega $
, implies that
$n \in \omega $
, implies that
![]() $R^{V[G]}$
is a semiscale on
$R^{V[G]}$
is a semiscale on
![]() $A^{V[G]}$
in
$A^{V[G]}$
in
![]() $V[G]$
.
$V[G]$
.
The following definition is used several times in the next section.
Definition 3.6. A set
![]() $\Gamma \subseteq \mathcal {P}(\omega ^\omega )$
has the semiscale property if every member of
$\Gamma \subseteq \mathcal {P}(\omega ^\omega )$
has the semiscale property if every member of
![]() $\Gamma $
has a semiscale which is coded by a continuous preimage of a member of
$\Gamma $
has a semiscale which is coded by a continuous preimage of a member of
![]() $\Gamma $
.
$\Gamma $
.
See Kechris and Moschovakis [Reference Kechris and Moschovakis8] or Moschovakis [Reference Moschovakis15] for more on semiscales.
4 Canonical models for universal Baireness
In this section, we continue to work in
![]() $\mathsf {ZF}$
. We show that if
$\mathsf {ZF}$
. We show that if
![]() $\Gamma \subseteq \mathrm {uB}$
and
$\Gamma \subseteq \mathrm {uB}$
and
![]() $\Gamma $
is selfdual and has the semiscale property, then there is an inclusion-minimal inner model containing
$\Gamma $
is selfdual and has the semiscale property, then there is an inclusion-minimal inner model containing
![]() $\mathbb {R}$
and
$\mathbb {R}$
and
![]() $\Gamma $
and satisfying the statement that every member of
$\Gamma $
and satisfying the statement that every member of
![]() $\Gamma $
is universally Baire. In the context of our main theorem, this minimal model has no sets of reals other than those in
$\Gamma $
is universally Baire. In the context of our main theorem, this minimal model has no sets of reals other than those in
![]() $\Gamma $
and therefore satisfies the statement that every set of reals is universally Baire.
$\Gamma $
and therefore satisfies the statement that every set of reals is universally Baire.
Definition 4.1. We let F be the class of all quadruples
![]() $(A,\mathbb {P},p,\dot {x})$
such that
$(A,\mathbb {P},p,\dot {x})$
such that
-
•
 $A \in \mathrm {uB}, \ \mathbb {P}$
is a poset,
$A \in \mathrm {uB}, \ \mathbb {P}$
is a poset,
 $p \in \mathbb {P},\ \dot {x}$
is a
$p \in \mathbb {P},\ \dot {x}$
is a
 $\mathbb {P}$
-name for a real, and
$\mathbb {P}$
-name for a real, and -
• p forces
 $\dot {x}$
to be in the canonical expansion of A.
$\dot {x}$
to be in the canonical expansion of A.
For sets
![]() $\Gamma \subseteq \mathrm {uB}$
, we define a local version of F that tells us how to compute the canonical extensions of sets in
$\Gamma \subseteq \mathrm {uB}$
, we define a local version of F that tells us how to compute the canonical extensions of sets in
![]() $\Gamma $
only:
$\Gamma $
only:
We will eventually (in Lemma 4.3) show that the desired minimal model is
![]() $L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R})$
, by which we mean the model constructed from the transitive set
$L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R})$
, by which we mean the model constructed from the transitive set
relative to the predicate
![]() $F \mathord {\restriction } \Gamma $
. First, we show that the sets in
$F \mathord {\restriction } \Gamma $
. First, we show that the sets in
![]() $\Gamma $
are universally Baire in this model when
$\Gamma $
are universally Baire in this model when
![]() $\Gamma $
is selfdual and has the semiscale property. In the proof, it will be important that the model knows how to expand not only the sets in
$\Gamma $
is selfdual and has the semiscale property. In the proof, it will be important that the model knows how to expand not only the sets in
![]() $\Gamma $
but also the relations coding semiscales on these sets and their complements.
$\Gamma $
but also the relations coding semiscales on these sets and their complements.
Theorem 4.2. If
![]() $\Gamma \subseteq \mathrm {uB}$
is selfdual and has the semiscale property, then
$\Gamma \subseteq \mathrm {uB}$
is selfdual and has the semiscale property, then
![]() $L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R}) \models \Gamma \subseteq \mathrm {uB}$
.
$L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R}) \models \Gamma \subseteq \mathrm {uB}$
.
Proof. Let
![]() $\mathcal {M}$
denote
$\mathcal {M}$
denote
![]() $L^{F \mathord {\restriction } \Gamma }(\mathbb {R}, \Gamma )$
, and fix
$L^{F \mathord {\restriction } \Gamma }(\mathbb {R}, \Gamma )$
, and fix
![]() $A \in \Gamma $
. Let
$A \in \Gamma $
. Let
![]() $\vec {\varphi }_+$
and
$\vec {\varphi }_+$
and
![]() $\vec {\varphi }_-$
be semiscales on A and
$\vec {\varphi }_-$
be semiscales on A and
![]() $\omega ^\omega \setminus A$
, respectively, such that the corresponding codes
$\omega ^\omega \setminus A$
, respectively, such that the corresponding codes
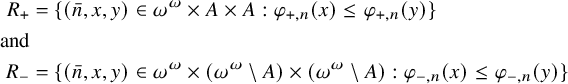 $$ \begin{align*} R_+ &= \{ (\bar{n}, x, y) \in \omega^{\omega} \times A \times A : \varphi_{+,n}(x) \le \varphi_{+,n}(y) \}\\ \text{and}\\ R_- &= \{ (\bar{n}, x, y) \in \omega^{\omega} \times (\omega^\omega \setminus A) \times (\omega^\omega \setminus A) : \varphi_{-,n}(x) \le \varphi_{-,n}(y) \} \end{align*} $$
$$ \begin{align*} R_+ &= \{ (\bar{n}, x, y) \in \omega^{\omega} \times A \times A : \varphi_{+,n}(x) \le \varphi_{+,n}(y) \}\\ \text{and}\\ R_- &= \{ (\bar{n}, x, y) \in \omega^{\omega} \times (\omega^\omega \setminus A) \times (\omega^\omega \setminus A) : \varphi_{-,n}(x) \le \varphi_{-,n}(y) \} \end{align*} $$
are in
![]() $\Gamma $
.
$\Gamma $
.
Consider an arbitrary set
![]() $Z \in \mathcal {M}$
. By Remark 2.3, it suffices to find a
$Z \in \mathcal {M}$
. By Remark 2.3, it suffices to find a
![]() $\mathrm {Col}(\omega ,Z)$
-absolutely complementing pair of trees for A in
$\mathrm {Col}(\omega ,Z)$
-absolutely complementing pair of trees for A in
![]() $\mathcal {M}$
. To do this, we will fix a V-generic filter
$\mathcal {M}$
. To do this, we will fix a V-generic filter
![]() $H \subseteq \mathrm {Col}(\omega ,Z)$
, find a complementing pair of trees for A in
$H \subseteq \mathrm {Col}(\omega ,Z)$
, find a complementing pair of trees for A in
![]() $\mathcal {M}[H]$
, and then show that these trees exist in
$\mathcal {M}[H]$
, and then show that these trees exist in
![]() $\mathcal {M}$
and are as desired.
$\mathcal {M}$
and are as desired.
Fixing H, we have by Lemma 3.5 that the expanded relations
![]() $R_+^{V[H]}$
and
$R_+^{V[H]}$
and
![]() $R_-^{V[H]}$
code semiscales on the expanded sets
$R_-^{V[H]}$
code semiscales on the expanded sets
![]() $A^{V[H]}$
and
$A^{V[H]}$
and
![]() $(\omega ^\omega \setminus A)^{V[H]}$
, respectively. Letting
$(\omega ^\omega \setminus A)^{V[H]}$
, respectively. Letting
![]() $\rho _+$
and
$\rho _+$
and
![]() $\rho _-$
be the standard
$\rho _-$
be the standard
![]() $\mathrm {Col}(\omega ,Z)$
-names for the canonical expansions of the relations
$\mathrm {Col}(\omega ,Z)$
-names for the canonical expansions of the relations
![]() $R_+$
and
$R_+$
and
![]() $R_-$
, respectively, we see that the restrictions
$R_-$
, respectively, we see that the restrictions
![]() $\rho _+ \cap \mathcal {M}$
and
$\rho _+ \cap \mathcal {M}$
and
![]() $\rho _- \cap \mathcal {M}$
are in
$\rho _- \cap \mathcal {M}$
are in
![]() $\mathcal {M}$
, as they are coded into the predicate
$\mathcal {M}$
, as they are coded into the predicate
![]() $F \mathord {\restriction } \Gamma $
. Therefore, the restricted relations
$F \mathord {\restriction } \Gamma $
. Therefore, the restricted relations
![]() $R_+^{V[H]} \cap {\mathcal {M}[H]}$
and
$R_+^{V[H]} \cap {\mathcal {M}[H]}$
and
![]() $R_-^{V[H]} \cap {\mathcal {M}[H]}$
are in the model
$R_-^{V[H]} \cap {\mathcal {M}[H]}$
are in the model
![]() $\mathcal {M}[H]$
. These restricted relations code semiscales
$\mathcal {M}[H]$
. These restricted relations code semiscales
![]() $\vec {\psi }_+,\vec {\psi }_- \in \mathcal {M}[H]$
on the sets
$\vec {\psi }_+,\vec {\psi }_- \in \mathcal {M}[H]$
on the sets
![]() $A^{V[H]} \cap {\mathcal {M}[H]}$
and
$A^{V[H]} \cap {\mathcal {M}[H]}$
and
![]() $(\omega ^\omega \setminus A)^{V[H]} \cap {\mathcal {M}[H]}$
, respectively, by Lemma 3.4. In
$(\omega ^\omega \setminus A)^{V[H]} \cap {\mathcal {M}[H]}$
, respectively, by Lemma 3.4. In
![]() $\mathcal {M}[H]$
, let
$\mathcal {M}[H]$
, let
![]() $S_+$
and
$S_+$
and
![]() $S_-$
be respectively the trees of the semiscales
$S_-$
be respectively the trees of the semiscales
![]() $\vec {\psi }_{+}$
and
$\vec {\psi }_{+}$
and
![]() $\vec {\psi }_{-}$
. It suffices to see that these trees are in
$\vec {\psi }_{-}$
. It suffices to see that these trees are in
![]() $\mathcal {M}$
and that they project to complements in any forcing extension of
$\mathcal {M}$
and that they project to complements in any forcing extension of
![]() $\mathcal {M}$
by
$\mathcal {M}$
by
![]() $\mathrm {Col}(\omega , Z)$
.
$\mathrm {Col}(\omega , Z)$
.
These two claims are proved by the same symmetry argument, showing that
![]() $S_{+}$
and
$S_{+}$
and
![]() $S_{-}$
do not depend on the generic filter H. More precisely, suppose toward a contradiction that there exist conditions
$S_{-}$
do not depend on the generic filter H. More precisely, suppose toward a contradiction that there exist conditions
![]() $p, p^{\prime } \in \mathrm {Col}(\omega , Z)$
, with
$p, p^{\prime } \in \mathrm {Col}(\omega , Z)$
, with
![]() $p \in H$
, which force contradictory statements about the membership of some sequence
$p \in H$
, which force contradictory statements about the membership of some sequence
![]() $\sigma $
(from
$\sigma $
(from
![]() $\mathcal {M}$
) in either of the trees
$\mathcal {M}$
) in either of the trees
![]() $S_{+}$
and
$S_{+}$
and
![]() $S_{-}$
, noting that these trees are definable in the
$S_{-}$
, noting that these trees are definable in the
![]() $\mathrm {Col}(\omega , Z)$
-extension of
$\mathrm {Col}(\omega , Z)$
-extension of
![]() $\mathcal {M}$
from the realizations of
$\mathcal {M}$
from the realizations of
![]() $\rho _{+} \cap \mathcal {M}$
and
$\rho _{+} \cap \mathcal {M}$
and
![]() $\rho _{-} \cap \mathcal {M}$
. By the symmetry of
$\rho _{-} \cap \mathcal {M}$
. By the symmetry of
![]() $\mathrm {Col}(\omega , Z)$
, there exists a V-generic filter
$\mathrm {Col}(\omega , Z)$
, there exists a V-generic filter
![]() $H^{\prime } \subseteq \mathrm {Col}(\omega , Z)$
, with
$H^{\prime } \subseteq \mathrm {Col}(\omega , Z)$
, with
![]() $p^{\prime } \in H^{\prime }$
, such that
$p^{\prime } \in H^{\prime }$
, such that
![]() $\bigcup H$
and
$\bigcup H$
and
![]() $\bigcup H^{\prime }$
differ by only finitely many coordinates, so that
$\bigcup H^{\prime }$
differ by only finitely many coordinates, so that
![]() $V[H] = V[H^{\prime }]$
and
$V[H] = V[H^{\prime }]$
and
![]() $\mathcal {M}[H] = \mathcal {M}[H^{\prime }]$
. We have then (by Remark 2.8) that
$\mathcal {M}[H] = \mathcal {M}[H^{\prime }]$
. We have then (by Remark 2.8) that
![]() $A^{V[H]} = A^{V[H^{\prime }]}, \ (\omega ^{\omega } \setminus A)^{V[H]} = (\omega ^{\omega } \setminus A)^{V[H^{\prime }]}, \ R_{+}^{V[H]} = R_{+}^{V[H^{\prime }]}$
and
$A^{V[H]} = A^{V[H^{\prime }]}, \ (\omega ^{\omega } \setminus A)^{V[H]} = (\omega ^{\omega } \setminus A)^{V[H^{\prime }]}, \ R_{+}^{V[H]} = R_{+}^{V[H^{\prime }]}$
and
![]() $R_{-}^{V[H]} = R_{-}^{V[H^{\prime }]}$
, from which it follows that the corresponding versions of
$R_{-}^{V[H]} = R_{-}^{V[H^{\prime }]}$
, from which it follows that the corresponding versions of
![]() $S_{+}$
and
$S_{+}$
and
![]() $S_{-}$
in
$S_{-}$
in
![]() $\mathcal {M}[H]$
and
$\mathcal {M}[H]$
and
![]() $\mathcal {M}[H^{\prime }]$
are the same, giving a contradiction. The same argument shows that no condition
$\mathcal {M}[H^{\prime }]$
are the same, giving a contradiction. The same argument shows that no condition
![]() $p^{\prime }$
can force that
$p^{\prime }$
can force that
![]() $S_{+}$
and
$S_{+}$
and
![]() $S_{-}$
fail to project to complements in a
$S_{-}$
fail to project to complements in a
![]() $\mathrm {Col}(\omega , Z)$
-extension of
$\mathrm {Col}(\omega , Z)$
-extension of
![]() $\mathcal {M}$
, since they do project to complements in
$\mathcal {M}$
, since they do project to complements in
![]() $\mathcal {M}[H]$
.
$\mathcal {M}[H]$
.
Next, we show that the definition of
![]() $F \mathord {\restriction } \Gamma $
is absolute to any inner model in which all sets in
$F \mathord {\restriction } \Gamma $
is absolute to any inner model in which all sets in
![]() $\Gamma $
are universally Baire. It follows that any such inner model must contain
$\Gamma $
are universally Baire. It follows that any such inner model must contain
![]() $L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R})$
.
$L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R})$
.
Lemma 4.3. Let
![]() $\Gamma \subseteq \mathrm {uB}$
. Let
$\Gamma \subseteq \mathrm {uB}$
. Let
![]() $\mathcal {M}$
be a model of
$\mathcal {M}$
be a model of
![]() $\mathsf {ZF}$
such that
$\mathsf {ZF}$
such that
and
![]() $\mathcal {M} \models \Gamma \subseteq \mathrm {uB}$
. Then
$\mathcal {M} \models \Gamma \subseteq \mathrm {uB}$
. Then
![]() $(F \mathord {\restriction } \Gamma )^{\mathcal {M}} = (F \mathord {\restriction } \Gamma ) \cap \mathcal {M}$
and
$(F \mathord {\restriction } \Gamma )^{\mathcal {M}} = (F \mathord {\restriction } \Gamma ) \cap \mathcal {M}$
and
![]() $L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R}) \subseteq \mathcal {M}$
.
$L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R}) \subseteq \mathcal {M}$
.
Proof. To show that
![]() $(F \mathord {\restriction } \Gamma )^{\mathcal {M}} = (F \mathord {\restriction } \Gamma ) \cap \mathcal {M}$
, fix
$(F \mathord {\restriction } \Gamma )^{\mathcal {M}} = (F \mathord {\restriction } \Gamma ) \cap \mathcal {M}$
, fix
![]() $A \in \Gamma $
and let
$A \in \Gamma $
and let
![]() $\mathbb {P}$
be a poset in
$\mathbb {P}$
be a poset in
![]() $\mathcal {M}$
. Let
$\mathcal {M}$
. Let
![]() $p \in \mathbb {P}$
, and let
$p \in \mathbb {P}$
, and let
![]() $\dot {x} \in \mathcal {M}$
be a
$\dot {x} \in \mathcal {M}$
be a
![]() $\mathbb {P}$
-name for a real. We claim that
$\mathbb {P}$
-name for a real. We claim that
Take a pair of trees
![]() $(T, \tilde {T}) \in \mathcal {M}$
witnessing that A is
$(T, \tilde {T}) \in \mathcal {M}$
witnessing that A is
![]() $\mathbb {P}$
-Baire in
$\mathbb {P}$
-Baire in
![]() $\mathcal {M}$
and take a pair of trees
$\mathcal {M}$
and take a pair of trees
![]() $(U,\tilde {U})$
witnessing that A is
$(U,\tilde {U})$
witnessing that A is
![]() $\mathbb {P}$
-Baire in V. Because
$\mathbb {P}$
-Baire in V. Because
![]() $\mathrm {p}[T] = \mathrm {p}[U] = A$
and
$\mathrm {p}[T] = \mathrm {p}[U] = A$
and
![]() $\mathrm {p}[\tilde {T}] = \mathrm {p}[\tilde {U}] = \omega ^\omega \setminus A$
in V and the pair
$\mathrm {p}[\tilde {T}] = \mathrm {p}[\tilde {U}] = \omega ^\omega \setminus A$
in V and the pair
![]() $(U,\tilde {U})$
is
$(U,\tilde {U})$
is
![]() $\mathbb {P}$
-absolutely complementing, Lemma 2.5 gives
$\mathbb {P}$
-absolutely complementing, Lemma 2.5 gives
We want to show that the following statements are equivalent for a condition
![]() $p \in \mathbb {P}$
and a
$p \in \mathbb {P}$
and a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {x}$
in
$\dot {x}$
in
![]() $\mathcal {M}$
:
$\mathcal {M}$
:
-
1.
 $\mathcal {M} \models p \mathbin {\Vdash } \dot {x} \in \mathrm {p}[T]$
;
$\mathcal {M} \models p \mathbin {\Vdash } \dot {x} \in \mathrm {p}[T]$
; -
2.
 $p \mathbin {\Vdash } \dot {x} \in \mathrm {p}[U]$
.
$p \mathbin {\Vdash } \dot {x} \in \mathrm {p}[U]$
.
To see this, assume first that (1) is true and take a V-generic filter
![]() $G \subseteq \mathbb {P}$
containing p. Because G is also
$G \subseteq \mathbb {P}$
containing p. Because G is also
![]() $\mathcal {M}$
-generic, we have
$\mathcal {M}$
-generic, we have
This shows that (2) is true.
Now assume that (1) is false, and take a condition
![]() $q \le p$
such that
$q \le p$
such that
Take a filter
![]() $G \subseteq \mathbb {P}$
containing q that is V-generic, and hence also M-generic. Then we have
$G \subseteq \mathbb {P}$
containing q that is V-generic, and hence also M-generic. Then we have
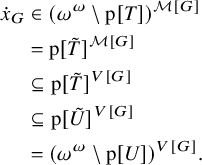 $$ \begin{align*} \dot{x}_G &\in (\omega^\omega \setminus \mathrm{p}[T])^{\mathcal{M}[G]}\\ &= \mathrm{p}[\tilde{T}]^{\mathcal{M}[G]}\\ &\subseteq \mathrm{p}[\tilde{T}]^{V[G]}\\ &\subseteq \mathrm{p}[\tilde{U}]^{V[G]}\\ &= (\omega^\omega \setminus \mathrm{p}[U])^{V[G]}. \end{align*} $$
$$ \begin{align*} \dot{x}_G &\in (\omega^\omega \setminus \mathrm{p}[T])^{\mathcal{M}[G]}\\ &= \mathrm{p}[\tilde{T}]^{\mathcal{M}[G]}\\ &\subseteq \mathrm{p}[\tilde{T}]^{V[G]}\\ &\subseteq \mathrm{p}[\tilde{U}]^{V[G]}\\ &= (\omega^\omega \setminus \mathrm{p}[U])^{V[G]}. \end{align*} $$
This shows that (2) is false.
To see that
![]() $L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R}) \subseteq \mathcal {M}$
, consider the model
$L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R}) \subseteq \mathcal {M}$
, consider the model
![]() $(L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R}))^{\mathcal {M}} = L^{(F \mathord {\restriction } \Gamma )^{\mathcal {M}}}(\Gamma , \mathbb {R})$
. It is contained in
$(L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R}))^{\mathcal {M}} = L^{(F \mathord {\restriction } \Gamma )^{\mathcal {M}}}(\Gamma , \mathbb {R})$
. It is contained in
![]() $\mathcal {M}$
, and its construction agrees with that of the model
$\mathcal {M}$
, and its construction agrees with that of the model
![]() $L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R})$
at every stage because
$L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R})$
at every stage because
![]() $(F \mathord {\restriction } \Gamma )^{\mathcal {M}} = (F \mathord {\restriction } \Gamma ) \cap \mathcal {M}$
.
$(F \mathord {\restriction } \Gamma )^{\mathcal {M}} = (F \mathord {\restriction } \Gamma ) \cap \mathcal {M}$
.
It follows that
![]() $L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R})$
sees the definition of F and therefore sees its own construction.
$L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R})$
sees the definition of F and therefore sees its own construction.
Corollary 4.4. Let
![]() $\Gamma \subseteq \mathrm {uB}$
. If
$\Gamma \subseteq \mathrm {uB}$
. If
![]() $\Gamma $
is selfdual and has the semiscale property, then the model
$\Gamma $
is selfdual and has the semiscale property, then the model
![]() $L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R})$
satisfies the statement
$L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R})$
satisfies the statement
![]() $V = L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R})$
.
$V = L^{F \mathord {\restriction } \Gamma }(\Gamma , \mathbb {R})$
.
5 A model of
 $\mathsf {ZF} + \mathsf {AD}^+ + {}$
‘every set of reals is universally Baire’
$\mathsf {ZF} + \mathsf {AD}^+ + {}$
‘every set of reals is universally Baire’
In this section, we present our main theorem and outline its proof. First, we recall some standard notation from the proof of Woodin’s Derived Model Theorem, as presented in Steel [Reference Steel23]. We let
![]() $\mathrm {ScS}$
denote the pointclass consisting of those
$\mathrm {ScS}$
denote the pointclass consisting of those
![]() $A \subseteq \omega ^{\omega }$
such that A and
$A \subseteq \omega ^{\omega }$
such that A and
![]() $\omega ^{\omega } \setminus A$
are both Suslin (i.e., such that A is Suslin and co-Suslin).
$\omega ^{\omega } \setminus A$
are both Suslin (i.e., such that A is Suslin and co-Suslin).
Definition 5.1. Let
![]() $\lambda $
be a limit of inaccessible cardinals, and let
$\lambda $
be a limit of inaccessible cardinals, and let
![]() $G \subseteq \mathrm {Col}(\omega ,\mathord {<}\lambda )$
be a V-generic filter. We define
$G \subseteq \mathrm {Col}(\omega ,\mathord {<}\lambda )$
be a V-generic filter. We define
-
•
 $\mathbb {R}^*_G$
to be
$\mathbb {R}^*_G$
to be
 $\bigcup _{\xi < \lambda } \mathbb {R}^{V[G \mathord {\restriction } \xi ]}$
.
$\bigcup _{\xi < \lambda } \mathbb {R}^{V[G \mathord {\restriction } \xi ]}$
. -
•
 $\mathrm {HC}^*_G$
to be
$\mathrm {HC}^*_G$
to be
 $\bigcup _{\xi < \lambda } \mathrm {HC}^{V[G \mathord {\restriction } \xi ]}$
, where
$\bigcup _{\xi < \lambda } \mathrm {HC}^{V[G \mathord {\restriction } \xi ]}$
, where
 $\mathrm {HC}$
denotes the collection of hereditarily countable sets.
$\mathrm {HC}$
denotes the collection of hereditarily countable sets. -
•
 $\mathrm {Hom}^*_G$
to be the pointclass consisting of all sets of the form
$\mathrm {Hom}^*_G$
to be the pointclass consisting of all sets of the form
 $\mathrm {p}[S] \cap \mathbb {R}^*_G$
, for some
$\mathrm {p}[S] \cap \mathbb {R}^*_G$
, for some
 $\lambda $
-absolutely complementing pairs of trees
$\lambda $
-absolutely complementing pairs of trees
 $(S,T)$
appearing in a model
$(S,T)$
appearing in a model
 $V[G \mathord {\restriction } \xi ]$
with
$V[G \mathord {\restriction } \xi ]$
with
 $\xi < \lambda $
.
$\xi < \lambda $
.
We define the symmetric extension
![]() $V(\mathbb {R}^*_G)$
to be
$V(\mathbb {R}^*_G)$
to be
![]() $\mathrm {HOD}_{V \cup \mathbb {R}^*_G \cup \{\mathbb {R}^*_G\}}^{V[G]}$
. By a theorem of Gödel proved in Section 5.2 of [Reference Schindler20],
$\mathrm {HOD}_{V \cup \mathbb {R}^*_G \cup \{\mathbb {R}^*_G\}}^{V[G]}$
. By a theorem of Gödel proved in Section 5.2 of [Reference Schindler20],
![]() $V(\mathbb {R}^{*}_{G})$
is a model of
$V(\mathbb {R}^{*}_{G})$
is a model of
![]() $\mathsf {ZF}$
. By the definition of the model,
$\mathsf {ZF}$
. By the definition of the model,
![]() $\mathbb {R}^*_G \subseteq \mathbb {R}^{V(\mathbb {R}^*_G)}$
. The reverse containment
$\mathbb {R}^*_G \subseteq \mathbb {R}^{V(\mathbb {R}^*_G)}$
. The reverse containment
![]() $\mathbb {R}^{*}_{G} \subseteq \mathbb {R}^{V(\mathbb {R}^{*}_{G})}$
follows from the homogeneity of
$\mathbb {R}^{*}_{G} \subseteq \mathbb {R}^{V(\mathbb {R}^{*}_{G})}$
follows from the homogeneity of
![]() $\mathrm {Col}(\omega , \mathord {<}\lambda )$
(by a standard argument which appears, for instance, on page 307 of [Reference Steel23]): each member x of
$\mathrm {Col}(\omega , \mathord {<}\lambda )$
(by a standard argument which appears, for instance, on page 307 of [Reference Steel23]): each member x of
![]() $\mathbb {R}^{V(\mathbb {R}^{*}_{G})}$
is definable in
$\mathbb {R}^{V(\mathbb {R}^{*}_{G})}$
is definable in
![]() $V[G]$
from
$V[G]$
from
![]() $\{\mathbb {R}^{*}_{G}\}$
and parameters existing in some model
$\{\mathbb {R}^{*}_{G}\}$
and parameters existing in some model
![]() $V[G \mathord {\restriction } \xi ]$
with
$V[G \mathord {\restriction } \xi ]$
with
![]() $\xi < \lambda $
, and the homogeneity of the remainder of
$\xi < \lambda $
, and the homogeneity of the remainder of
![]() $\mathrm {Col}(\omega , \mathord {<}\lambda )$
after
$\mathrm {Col}(\omega , \mathord {<}\lambda )$
after
![]() $\xi $
implies that x exists already in
$\xi $
implies that x exists already in
![]() $V[G \mathord {\restriction } \xi ]$
.
$V[G \mathord {\restriction } \xi ]$
.
A similar homogeneity argument shows that
![]() $\mathrm {ScS}^{V(\mathbb {R}^*_G)} \subseteq \mathrm {Hom}^*_G$
, since any pair of trees witnessing membership in
$\mathrm {ScS}^{V(\mathbb {R}^*_G)} \subseteq \mathrm {Hom}^*_G$
, since any pair of trees witnessing membership in
![]() $\mathrm {ScS}^{V(\mathbb {R}^*_G)}$
would exist in some such
$\mathrm {ScS}^{V(\mathbb {R}^*_G)}$
would exist in some such
![]() $V[G \mathord {\restriction } \xi ]$
(being definable in
$V[G \mathord {\restriction } \xi ]$
(being definable in
![]() $V[G]$
from
$V[G]$
from
![]() $\{\mathbb {R}^{*}_{G}\}$
and parameters in such a model), and would have to be
$\{\mathbb {R}^{*}_{G}\}$
and parameters in such a model), and would have to be
![]() $\lambda $
-absolutely complementing in order to project to complements in
$\lambda $
-absolutely complementing in order to project to complements in
![]() $V(\mathbb {R}^{*}_{G})$
. Finally,
$V(\mathbb {R}^{*}_{G})$
. Finally,
![]() $\mathrm {Hom}^{*}_{G} \subseteq \mathrm {ScS}^{V(\mathbb {R}^{*}_{G})}$
since
$\mathrm {Hom}^{*}_{G} \subseteq \mathrm {ScS}^{V(\mathbb {R}^{*}_{G})}$
since
![]() $V(\mathbb {R}^{*}_{G})$
contains each model
$V(\mathbb {R}^{*}_{G})$
contains each model
![]() $V[G \mathord {\restriction } \xi ] (\xi < \lambda )$
.
$V[G \mathord {\restriction } \xi ] (\xi < \lambda )$
.
With these definitions in hand, we can state the main theorem of this paper.
Theorem 5.2. Let
![]() $\lambda $
be a limit of Woodin cardinals and a limit of strong cardinals, let
$\lambda $
be a limit of Woodin cardinals and a limit of strong cardinals, let
![]() $G \subseteq \mathrm {Col}(\omega ,\mathord {<}\lambda )$
be a V-generic filter, and let
$G \subseteq \mathrm {Col}(\omega ,\mathord {<}\lambda )$
be a V-generic filter, and let
![]() $\mathcal {M}$
be the model
$\mathcal {M}$
be the model
where
![]() $L^F(\mathbb {R}^*_G, \mathrm {Hom}^*_G)$
denotes the class of all sets constructible from the transitive set
$L^F(\mathbb {R}^*_G, \mathrm {Hom}^*_G)$
denotes the class of all sets constructible from the transitive set
![]() $V_\omega \cup \mathbb {R}^*_G \cup \mathrm {Hom}^*_G$
relative to the predicate F. Then the following hold.
$V_\omega \cup \mathbb {R}^*_G \cup \mathrm {Hom}^*_G$
relative to the predicate F. Then the following hold.
-
1.
 $\mathcal {M} \models \mathsf {AD}_{\mathbb {R}}$
.
$\mathcal {M} \models \mathsf {AD}_{\mathbb {R}}$
. -
2.
 $\mathcal {P}(\mathbb {R})^{\mathcal {M}} = \mathrm {Hom}^*_G$
$\mathcal {P}(\mathbb {R})^{\mathcal {M}} = \mathrm {Hom}^*_G$
-
3.
 $\mathcal {M} \models {}$
‘every set of reals is universally Baire’.
$\mathcal {M} \models {}$
‘every set of reals is universally Baire’. -
4.
 $\mathcal {M} \models V = \mathrm {HOD}_{\mathcal {P}(\mathbb {R})}$
.
$\mathcal {M} \models V = \mathrm {HOD}_{\mathcal {P}(\mathbb {R})}$
.
Moreover,
![]() $\mathcal {M}$
has the following minimality property: if
$\mathcal {M}$
has the following minimality property: if
![]() $\mathcal {M}^{\prime } \subseteq V(\mathbb {R}^{*}_{G})$
is a model of
$\mathcal {M}^{\prime } \subseteq V(\mathbb {R}^{*}_{G})$
is a model of
![]() $\mathsf {ZF} + {}$
‘every set of reals is universally Baire’ such that
$\mathsf {ZF} + {}$
‘every set of reals is universally Baire’ such that
then
![]() $\mathcal {M} \subseteq \mathcal {M}^{\prime }$
.
$\mathcal {M} \subseteq \mathcal {M}^{\prime }$
.
Remark 5.3. By results of Moschovakis and Woodin (see Theorem 0.3 of [Reference Larson11]), the theory
![]() $\mathsf {ZF}$
+
$\mathsf {ZF}$
+
![]() $\mathsf {AD}$
+ all sets of reals are Suslin implies
$\mathsf {AD}$
+ all sets of reals are Suslin implies
![]() $\mathsf {AD}^{+}$
(whose definition we give below). So
$\mathsf {AD}^{+}$
(whose definition we give below). So
![]() $\mathsf {AD}^{+}$
holds in the model
$\mathsf {AD}^{+}$
holds in the model
![]() $\mathcal {M}$
from our Main Theorem. By results of Martin and Woodin (Theorem 13.1 of [Reference Larson11]), the theory
$\mathcal {M}$
from our Main Theorem. By results of Martin and Woodin (Theorem 13.1 of [Reference Larson11]), the theory
![]() $\mathsf {ZF}$
+
$\mathsf {ZF}$
+
![]() $\mathsf {AD}$
+ all sets of reals are Suslin implies
$\mathsf {AD}$
+ all sets of reals are Suslin implies
![]() $\mathsf {AD}_{\mathbb {R}}$
. So part (1) of the main theorem follows from part (3) plus the fact that
$\mathsf {AD}_{\mathbb {R}}$
. So part (1) of the main theorem follows from part (3) plus the fact that
![]() $\mathcal {M} \models \mathsf {AD}$
. We will in fact prove that
$\mathcal {M} \models \mathsf {AD}$
. We will in fact prove that
![]() $\mathcal {M} \models \mathsf {AD}^{+}$
on the way to proving part (3) of the main theorem.
$\mathcal {M} \models \mathsf {AD}^{+}$
on the way to proving part (3) of the main theorem.
Remark 5.4. A theorem of Woodin from the 1980s (Theorem 7.1 of [Reference Steel23]) says, using the notation above, that if
![]() $\lambda $
is a limit of Woodin cardinals, then
$\lambda $
is a limit of Woodin cardinals, then
![]() $L(\mathbb {R}^{*}_{G}, \mathrm {Hom}^{*}_{G}) \models \mathsf {AD}^{+}$
and
$L(\mathbb {R}^{*}_{G}, \mathrm {Hom}^{*}_{G}) \models \mathsf {AD}^{+}$
and
![]() $\mathrm {Hom}^{*}_{G}$
is
$\mathrm {Hom}^{*}_{G}$
is
![]() $\mathrm {ScS}^{L(\mathbb {R}^{*}_{G}, \mathrm {Hom}^{*}_{G})}$
. The model
$\mathrm {ScS}^{L(\mathbb {R}^{*}_{G}, \mathrm {Hom}^{*}_{G})}$
. The model
![]() $L(\mathbb {R}^{*}_{G}, \mathrm {Hom}^{*}_{G})$
is sometimes referred to as the old derived model. This is to contrast it with the (larger) new derived model
$L(\mathbb {R}^{*}_{G}, \mathrm {Hom}^{*}_{G})$
is sometimes referred to as the old derived model. This is to contrast it with the (larger) new derived model
![]() $D(V, \lambda , G)$
; that is,
$D(V, \lambda , G)$
; that is,
![]() $L(\Gamma _{+}, \mathbb {R}^{*}_{G})$
, where
$L(\Gamma _{+}, \mathbb {R}^{*}_{G})$
, where
![]() $\Gamma _{+}$
is the set of
$\Gamma _{+}$
is the set of
![]() $B \subseteq \mathbb {R}^{*}_{G}$
in
$B \subseteq \mathbb {R}^{*}_{G}$
in
![]() $V(\mathbb {R}^{*}_{G})$
for which
$V(\mathbb {R}^{*}_{G})$
for which
![]() $L(B, \mathbb {R}^{*}_{G}) \models \mathsf {AD}^{+}$
. Theorem 31 of [Reference Woodin24] says that
$L(B, \mathbb {R}^{*}_{G}) \models \mathsf {AD}^{+}$
. Theorem 31 of [Reference Woodin24] says that
![]() $D(V, \lambda , G) \models \mathsf {AD}^{+}$
, again under the assumption that
$D(V, \lambda , G) \models \mathsf {AD}^{+}$
, again under the assumption that
![]() $\lambda $
is a limit of Woodin cardinals. The hypotheses of our main theorem imply (via Theorem 9.1) that the old and new derived models are equal (see Remark 9.2).
$\lambda $
is a limit of Woodin cardinals. The hypotheses of our main theorem imply (via Theorem 9.1) that the old and new derived models are equal (see Remark 9.2).
Before starting the proof of the main theorem, we review some material on homogeneously Suslin sets of reals (which is presented in more detail in [Reference Larson10, Reference Steel23]). A tree of measures (on an ordinal
![]() $\gamma $
, the choice of which will usually not concern us) is a family
$\gamma $
, the choice of which will usually not concern us) is a family
![]() $\langle \mu _s : s \in \omega ^{\mathord {<}\omega }\rangle $
of measures such that each measure
$\langle \mu _s : s \in \omega ^{\mathord {<}\omega }\rangle $
of measures such that each measure
![]() $\mu _s$
concentrates on the set
$\mu _s$
concentrates on the set
![]() $\gamma ^{\left |s\right |}$
and such that
$\gamma ^{\left |s\right |}$
and such that
![]() $\mu _t$
projects to
$\mu _t$
projects to
![]() $\mu _s$
whenever t extends s, meaning that for each
$\mu _s$
whenever t extends s, meaning that for each
![]() $A \in \mu _{s}$
, the set of
$A \in \mu _{s}$
, the set of
![]() $\sigma \in \gamma ^{|t|}$
with
$\sigma \in \gamma ^{|t|}$
with
![]() $\sigma \mathord {\restriction } |s| \in A$
is in
$\sigma \mathord {\restriction } |s| \in A$
is in
![]() $\mu _{t}$
. Given a tree of measures
$\mu _{t}$
. Given a tree of measures
![]() $\vec {\mu } = \langle \mu _s : s \in \omega ^{\mathord {<}\omega }\rangle $
, for every real x, we let
$\vec {\mu } = \langle \mu _s : s \in \omega ^{\mathord {<}\omega }\rangle $
, for every real x, we let
![]() $\vec {\mu }_x$
denote the tower (i.e., projecting sequence) of measures
$\vec {\mu }_x$
denote the tower (i.e., projecting sequence) of measures
![]() $\langle \mu _{x \mathord {\restriction } n} : n<\omega \rangle $
. We define the set of reals
$\langle \mu _{x \mathord {\restriction } n} : n<\omega \rangle $
. We define the set of reals
![]() $\textbf {S}_{\vec {\mu }}$
to be the set of
$\textbf {S}_{\vec {\mu }}$
to be the set of
![]() $x \in \omega ^\omega $
for which
$x \in \omega ^\omega $
for which
![]() $\vec {\mu }_x$
is wellfounded (i.e., for which the direct limit of the
$\vec {\mu }_x$
is wellfounded (i.e., for which the direct limit of the
![]() $\mu _{x \mathord {\restriction } n}$
-ultrapowers of V (for
$\mu _{x \mathord {\restriction } n}$
-ultrapowers of V (for
![]() $n \in \omega $
) induced by the projection maps is wellfounded). Given a cardinal
$n \in \omega $
) induced by the projection maps is wellfounded). Given a cardinal
![]() $\kappa $
, a set of reals A is said to be
$\kappa $
, a set of reals A is said to be
![]() $\kappa $
-homogeneous if
$\kappa $
-homogeneous if
![]() $A = \textbf {S}_{\vec {\mu }}$
for some tree
$A = \textbf {S}_{\vec {\mu }}$
for some tree
![]() $\vec {\mu }$
of
$\vec {\mu }$
of
![]() $\kappa $
-complete measures.
$\kappa $
-complete measures.
By an observation of Woodin (see Steel [Reference Steel23, Proposition 2.5]), every tree
![]() $\vec {\mu }$
of
$\vec {\mu }$
of
![]() $\kappa $
-complete measures on
$\kappa $
-complete measures on
![]() $\gamma $
is a
$\gamma $
is a
![]() $\kappa $
-homogeneity system for some tree T on
$\kappa $
-homogeneity system for some tree T on
![]() $\omega \times \gamma $
, meaning that each measure
$\omega \times \gamma $
, meaning that each measure
![]() $\mu _s$
concentrates on the set
$\mu _s$
concentrates on the set
![]() $T \cap \gamma ^{\left |s\right |}$
, and for every real
$T \cap \gamma ^{\left |s\right |}$
, and for every real
![]() $x \in \mathrm {p}[T],$
the tower
$x \in \mathrm {p}[T],$
the tower
![]() $\vec {\mu }_x$
is wellfounded. For every real
$\vec {\mu }_x$
is wellfounded. For every real
![]() $x \notin \mathrm {p}[T]$
then the tower
$x \notin \mathrm {p}[T]$
then the tower
![]() $\vec {\mu }_x$
must be ill-founded, so
$\vec {\mu }_x$
must be ill-founded, so
![]() $S_{\vec {\mu }} = \mathrm {p}[T]$
. So all
$S_{\vec {\mu }} = \mathrm {p}[T]$
. So all
![]() $\kappa $
-homogeneous sets of reals are Suslin, and they are sometimes called
$\kappa $
-homogeneous sets of reals are Suslin, and they are sometimes called
![]() $\kappa $
-homogeneously Suslin to emphasize this property. In the weakest nontrivial case, when
$\kappa $
-homogeneously Suslin to emphasize this property. In the weakest nontrivial case, when
![]() $\kappa = \omega _{1}$
, we say that A is homogeneously Suslin.
$\kappa = \omega _{1}$
, we say that A is homogeneously Suslin.
By the Levy-Solovay theorem, for every generic extension
![]() $V[g]$
of V by a poset of size less than
$V[g]$
of V by a poset of size less than
![]() $\kappa $
, every
$\kappa $
, every
![]() $\kappa $
-complete
$\kappa $
-complete
![]() $\mu \in V$
induces a corresponding measure
$\mu \in V$
induces a corresponding measure
![]() $\hat {\mu }$
in
$\hat {\mu }$
in
![]() $V[g]$
, and the ultrapower of the ordinals by
$V[g]$
, and the ultrapower of the ordinals by
![]() $\mu $
in V agrees with the ultrapower of the ordinals by
$\mu $
in V agrees with the ultrapower of the ordinals by
![]() $\hat {\mu }$
in
$\hat {\mu }$
in
![]() $V[g]$
. (Henceforth, we will denote both measures by
$V[g]$
. (Henceforth, we will denote both measures by
![]() $\mu $
where it will not cause confusion.) So we can also define the set
$\mu $
where it will not cause confusion.) So we can also define the set
![]() $\textbf {S}_{\vec {\mu }}$
in small generic extensions, and we have
$\textbf {S}_{\vec {\mu }}$
in small generic extensions, and we have
![]() $(\textbf {S}_{\vec {\mu }})^{V[g]} \cap V = (\textbf {S}_{\vec {\mu }})^V$
.
$(\textbf {S}_{\vec {\mu }})^{V[g]} \cap V = (\textbf {S}_{\vec {\mu }})^V$
.
Given a tree
![]() $\vec {\mu }$
of measures, the Martin–Solovay tree
$\vec {\mu }$
of measures, the Martin–Solovay tree
![]() $\operatorname {\mathrm {ms}}(\vec {\mu })$
is the tree of attempts to build a real x and a sequence of ordinals witnessing the ill-foundedness of the corresponding tower
$\operatorname {\mathrm {ms}}(\vec {\mu })$
is the tree of attempts to build a real x and a sequence of ordinals witnessing the ill-foundedness of the corresponding tower
![]() $\vec {\mu }_x$
(see [Reference Steel23, Reference Larson10] for a precise definition.) The Martin–Solovay tree has the key property that
$\vec {\mu }_x$
(see [Reference Steel23, Reference Larson10] for a precise definition.) The Martin–Solovay tree has the key property that
If the measures in
![]() $\vec {\mu }$
are
$\vec {\mu }$
are
![]() $\kappa $
-complete, then definition of the Martin–Solovay tree is absolute to generic extensions via posets of cardinality less than
$\kappa $
-complete, then definition of the Martin–Solovay tree is absolute to generic extensions via posets of cardinality less than
![]() $\kappa $
, so the equality
$\kappa $
, so the equality
![]() $\textbf {S}_{\vec {\mu }} = \omega ^\omega \setminus \mathrm {p}[\operatorname {\mathrm {ms}}(\vec {\mu })]$
continues to hold in such extensions. It follows that for any tree T carrying a homogeneity system
$\textbf {S}_{\vec {\mu }} = \omega ^\omega \setminus \mathrm {p}[\operatorname {\mathrm {ms}}(\vec {\mu })]$
continues to hold in such extensions. It follows that for any tree T carrying a homogeneity system
![]() $\vec {\mu }$
consisting of
$\vec {\mu }$
consisting of
![]() $\kappa $
-complete measures, the pair
$\kappa $
-complete measures, the pair
![]() $(T, \operatorname {\mathrm {ms}}(\vec {\mu }))$
is
$(T, \operatorname {\mathrm {ms}}(\vec {\mu }))$
is
![]() $\kappa $
-absolutely complementing. This implies that every
$\kappa $
-absolutely complementing. This implies that every
![]() $\kappa $
-homogeneous set of reals
$\kappa $
-homogeneous set of reals
![]() $A = \textbf {S}_{\vec {\mu }}$
is
$A = \textbf {S}_{\vec {\mu }}$
is
![]() $\kappa $
-universally Baire, and that whenever
$\kappa $
-universally Baire, and that whenever
![]() $V[g]$
is a generic extension of V by a poset of size less than
$V[g]$
is a generic extension of V by a poset of size less than
![]() $\kappa $
, we have
$\kappa $
, we have
![]() $A^{V[g]} = (\textbf {S}_{\vec {\mu }})^{V[g]}$
. In other words, the canonical extension of A given by
$A^{V[g]} = (\textbf {S}_{\vec {\mu }})^{V[g]}$
. In other words, the canonical extension of A given by
![]() $\kappa $
-homogeneity agrees with that given by
$\kappa $
-homogeneity agrees with that given by
![]() $\kappa $
-universal Baireness.
$\kappa $
-universal Baireness.
Another property of the Martin–Solovay tree that we will use is the fact that its definition from
![]() $\vec {\mu }$
is continuous: for every
$\vec {\mu }$
is continuous: for every
![]() $n<\omega $
, the subtree
$n<\omega $
, the subtree
![]() $\operatorname {\mathrm {ms}}(\vec {\mu }) \mathord {\restriction } n$
consisting of the first n levels of
$\operatorname {\mathrm {ms}}(\vec {\mu }) \mathord {\restriction } n$
consisting of the first n levels of
![]() $\operatorname {\mathrm {ms}}(\vec {\mu })$
is determined by finitely many measures from
$\operatorname {\mathrm {ms}}(\vec {\mu })$
is determined by finitely many measures from
![]() $\vec {\mu }$
.
$\vec {\mu }$
.
Remark 5.5. If
![]() $\kappa $
is a cardinal and
$\kappa $
is a cardinal and
![]() $\delta _0$
and
$\delta _0$
and
![]() $\delta _1$
are Woodin cardinals with
$\delta _1$
are Woodin cardinals with
![]() $\kappa < \delta _0 < \delta _1$
, then every
$\kappa < \delta _0 < \delta _1$
, then every
![]() $\delta _1^+$
-universally Baire set of reals is
$\delta _1^+$
-universally Baire set of reals is
![]() $\kappa $
-homogeneously Suslin. This follows by combining a theorem of Woodin (see Larson [Reference Larson10, Theorem 3.3.8] or Steel [Reference Steel23, Theorem 4.1]) with a theorem of Martin and Steel [Reference Martin and Steel12]. In particular, if
$\kappa $
-homogeneously Suslin. This follows by combining a theorem of Woodin (see Larson [Reference Larson10, Theorem 3.3.8] or Steel [Reference Steel23, Theorem 4.1]) with a theorem of Martin and Steel [Reference Martin and Steel12]. In particular, if
![]() $\lambda $
is a limit of Woodin cardinals, then every
$\lambda $
is a limit of Woodin cardinals, then every
![]() $\lambda $
-universally Baire set of reals is
$\lambda $
-universally Baire set of reals is
![]() $\mathord {<}\lambda $
-homogenously Suslin (i.e.,
$\mathord {<}\lambda $
-homogenously Suslin (i.e.,
![]() $\kappa $
-homogeneous for all
$\kappa $
-homogeneous for all
![]() $\kappa < \lambda $
; we write
$\kappa < \lambda $
; we write
![]() $\mathrm {Hom}_{\mathord {<}\lambda }$
for the set of
$\mathrm {Hom}_{\mathord {<}\lambda }$
for the set of
![]() $\mathord {<}\lambda $
-homgeneously Suslin sets of reals). As outlined above, the reverse inclusion follows from the Martin–Solovay construction.
$\mathord {<}\lambda $
-homgeneously Suslin sets of reals). As outlined above, the reverse inclusion follows from the Martin–Solovay construction.
We now proceed to give the proof of the main theorem, assuming three facts that will be proved in later sections. As in the proof of the Derived Model Theorem, part (1) will be obtained as an immediate consequence of a
![]() $\Sigma ^2_1$
reflection property of the model
$\Sigma ^2_1$
reflection property of the model
![]() $\mathcal {M}$
, as follows.
$\mathcal {M}$
, as follows.
Lemma 5.6 (8.1).
Let
![]() $\lambda $
be a limit of Woodin cardinals and a limit of strong cardinals, let
$\lambda $
be a limit of Woodin cardinals and a limit of strong cardinals, let
![]() $G \subseteq \mathrm {Col}(\omega ,\mathord {<}\lambda )$
be a V-generic filter, and let
$G \subseteq \mathrm {Col}(\omega ,\mathord {<}\lambda )$
be a V-generic filter, and let
![]() $\mathcal {M}$
be the model
$\mathcal {M}$
be the model
![]() $L^F(\mathbb {R}^*_G, \mathrm {Hom}^*_G)^{V(\mathbb {R}^*_G)}$
. For every sentence
$L^F(\mathbb {R}^*_G, \mathrm {Hom}^*_G)^{V(\mathbb {R}^*_G)}$
. For every sentence
![]() $\varphi $
, if there is a set of reals
$\varphi $
, if there is a set of reals
![]() $A\in \mathcal {M}$
such that
$A\in \mathcal {M}$
such that
![]() $(\mathrm {HC}^*_G,\mathord {\in },A) \models \varphi $
, then there is a set of reals
$(\mathrm {HC}^*_G,\mathord {\in },A) \models \varphi $
, then there is a set of reals
![]() $A \in \mathrm {Hom}_{\mathord {<}\lambda }^V$
such that
$A \in \mathrm {Hom}_{\mathord {<}\lambda }^V$
such that
![]() $(\mathrm {HC}^{V},\mathord {\in },A) \models \varphi $
.
$(\mathrm {HC}^{V},\mathord {\in },A) \models \varphi $
.
Taking Lemma 8.1 for granted, we immediately get that
![]() $\mathcal {M} \models \mathsf {AD}$
, since
$\mathcal {M} \models \mathsf {AD}$
, since
![]() $\mathord {<}\lambda $
-homogeneously Suslin sets of reals are determined whenever
$\mathord {<}\lambda $
-homogeneously Suslin sets of reals are determined whenever
![]() $\lambda $
is greater than a measurable cardinal, a fact which was essentially shown by Martin in the course of proving determinacy for
$\lambda $
is greater than a measurable cardinal, a fact which was essentially shown by Martin in the course of proving determinacy for
![]() $\mathbf {\Pi }^1_1$
sets of reals from a measurable cardinal (see Theorem 33.31 of [Reference Jech4] or Exercise 32.2 of [Reference Kanamori5]).
$\mathbf {\Pi }^1_1$
sets of reals from a measurable cardinal (see Theorem 33.31 of [Reference Jech4] or Exercise 32.2 of [Reference Kanamori5]).
Lemma 8.1 also implies that
![]() $\mathcal {M} \models \mathsf {AD}^{+}$
. One way to see this is to note that
$\mathcal {M} \models \mathsf {AD}^{+}$
. One way to see this is to note that
![]() $\mathsf {AD}^+$
can be reformulated as a
$\mathsf {AD}^+$
can be reformulated as a
![]() $\Pi ^2_1$
statement that is true in the pointclass
$\Pi ^2_1$
statement that is true in the pointclass
![]() $\mathrm {Hom}_{\mathord {<}\lambda }^V$
. In more (standard) detail, the axiom
$\mathrm {Hom}_{\mathord {<}\lambda }^V$
. In more (standard) detail, the axiom
![]() $\mathsf {AD}^{+}$
is the conjunction of the following three statements:
$\mathsf {AD}^{+}$
is the conjunction of the following three statements:
-
•
 $\mathsf {DC}_{\mathbb {R}}$
$\mathsf {DC}_{\mathbb {R}}$
-
• Every set of reals is
 $\infty $
-Borel.
$\infty $
-Borel. -
•
 $\mathord {<}\Theta $
-Determinacy.
$\mathord {<}\Theta $
-Determinacy.
The axiom
![]() $\mathsf {DC}_{\mathbb {R}}$
says that every tree on
$\mathsf {DC}_{\mathbb {R}}$
says that every tree on
![]() $\mathbb {R}$
without terminal nodes has an infinite branch. Using a pairing function on
$\mathbb {R}$
without terminal nodes has an infinite branch. Using a pairing function on
![]() $\mathbb {R}$
, we can represent such a tree T with the set A of reals coding sequences in T. Since homogeneously Suslin sets are Suslin, they can be uniformized. It follows that if A is homogeneously Suslin, then there is a function f picking for each
$\mathbb {R}$
, we can represent such a tree T with the set A of reals coding sequences in T. Since homogeneously Suslin sets are Suslin, they can be uniformized. It follows that if A is homogeneously Suslin, then there is a function f picking for each
![]() $x \in A$
a
$x \in A$
a
![]() $y \in A$
coding a proper extension in T of the node coded by x. Starting with any
$y \in A$
coding a proper extension in T of the node coded by x. Starting with any
![]() $x \in A$
and coding the sequence
$x \in A$
and coding the sequence
![]() $\langle f^{i}(x) : i \in \omega \rangle $
with a real, we get that an infinite branch through A exists in
$\langle f^{i}(x) : i \in \omega \rangle $
with a real, we get that an infinite branch through A exists in
![]() $(\mathrm {HC}, \in , A)$
. This shows that
$(\mathrm {HC}, \in , A)$
. This shows that
![]() $\mathsf {DC}_{\mathbb {R}}$
holds (in V) for all trees on
$\mathsf {DC}_{\mathbb {R}}$
holds (in V) for all trees on
![]() $\mathbb {R}$
coded by homogeneously Suslin trees. Lemma 8.1 then implies that it holds for all trees on
$\mathbb {R}$
coded by homogeneously Suslin trees. Lemma 8.1 then implies that it holds for all trees on
![]() $\mathbb {R}$
in
$\mathbb {R}$
in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Similarly,
![]() $\mathsf {AD}$
implies that
$\mathsf {AD}$
implies that
![]() $\mathord {<}\Theta $
-Determinacy holds for games with Suslin, co-Suslin payoff (see Corollary 7.3 of [Reference Larson11]). Since
$\mathord {<}\Theta $
-Determinacy holds for games with Suslin, co-Suslin payoff (see Corollary 7.3 of [Reference Larson11]). Since
![]() $\mathord {<}\lambda $
-homogeneously Suslin sets are Suslin and co-Suslin (being
$\mathord {<}\lambda $
-homogeneously Suslin sets are Suslin and co-Suslin (being
![]() $\mathord {<}\lambda $
-universally Baire by the remarks above), and the games referred to in the definition of
$\mathord {<}\lambda $
-universally Baire by the remarks above), and the games referred to in the definition of
![]() $\mathord {<}\Theta $
-Determinacy can be coded by sets of reals, Lemma 8.1 then implies that
$\mathord {<}\Theta $
-Determinacy can be coded by sets of reals, Lemma 8.1 then implies that
![]() $\mathord {<}\Theta $
-Determinacy holds in
$\mathord {<}\Theta $
-Determinacy holds in
![]() $\mathcal {M}$
. Finally, the arguments in Section 8.2 of [Reference Larson11] show that if a set
$\mathcal {M}$
. Finally, the arguments in Section 8.2 of [Reference Larson11] show that if a set
![]() $A \subseteq \omega ^{\omega }$
is
$A \subseteq \omega ^{\omega }$
is
![]() $\infty $
-Borel, then A has an
$\infty $
-Borel, then A has an
![]() $\infty $
-Borel code coded by a set of reals which is
$\infty $
-Borel code coded by a set of reals which is
![]() $\mathbf {\Sigma }^{1}_{1}$
in a prewellordering which is Wadge below either A or its complement (i.e., one coded in the structure
$\mathbf {\Sigma }^{1}_{1}$
in a prewellordering which is Wadge below either A or its complement (i.e., one coded in the structure
![]() $(\mathrm {HC}, \in , A)$
). Every homogeneously Suslin set A is Suslin and therefore has an
$(\mathrm {HC}, \in , A)$
). Every homogeneously Suslin set A is Suslin and therefore has an
![]() $\infty $
-Borel code definable over
$\infty $
-Borel code definable over
![]() $(\mathrm {HC}, \in A)$
.
$(\mathrm {HC}, \in A)$
.
The proof of the
![]() $\Sigma ^2_1$
reflection property (i.e., Lemma 8.1) is the most technically demanding part of this paper. It will be given in Section 8 after some background information and preliminary work are presented in Sections 6 and 7, respectively. Our proof will be similar to that given by Steel [Reference Steel, Gao, Jackson and Zhang22] for the model
$\Sigma ^2_1$
reflection property (i.e., Lemma 8.1) is the most technically demanding part of this paper. It will be given in Section 8 after some background information and preliminary work are presented in Sections 6 and 7, respectively. Our proof will be similar to that given by Steel [Reference Steel, Gao, Jackson and Zhang22] for the model
![]() $L(\mathbb {R}^*_G, \mathrm {Hom}^*_G)$
. Roughly speaking, the proof can be adapted to the model
$L(\mathbb {R}^*_G, \mathrm {Hom}^*_G)$
. Roughly speaking, the proof can be adapted to the model
![]() $\mathcal {M}$
because the information added by the predicate F is canonical.
$\mathcal {M}$
because the information added by the predicate F is canonical.
Next, we outline the proof of part (2) of the main theorem. It suffices to prove the inclusion
![]() $\mathcal {P}(\mathbb {R})^{\mathcal {M}} \subseteq \mathrm {Hom}^*_G$
, since the reverse inclusion holds by the definition of the model
$\mathcal {P}(\mathbb {R})^{\mathcal {M}} \subseteq \mathrm {Hom}^*_G$
, since the reverse inclusion holds by the definition of the model
![]() $\mathcal {M}$
. Let A be a set of reals in
$\mathcal {M}$
. Let A be a set of reals in
![]() $\mathcal {M}$
. Note that
$\mathcal {M}$
. Note that
![]() $\mathsf {AD}^+$
holds in the model
$\mathsf {AD}^+$
holds in the model
![]() $L(A,\mathbb {R}^*_G)$
since it holds in
$L(A,\mathbb {R}^*_G)$
since it holds in
![]() $\mathcal {M}$
, and due to its equivalent
$\mathcal {M}$
, and due to its equivalent
![]() $\Pi ^2_1$
reformulation,
$\Pi ^2_1$
reformulation,
![]() $\mathsf {AD}^{+}$
is downward absolute to transitive inner models with the same reals (Theorem 8.22 of [Reference Larson11]). Therefore, A is in the new derived model
$\mathsf {AD}^{+}$
is downward absolute to transitive inner models with the same reals (Theorem 8.22 of [Reference Larson11]). Therefore, A is in the new derived model
![]() $D(V,\lambda ,G)$
(which was defined in Remark 5.4). Since
$D(V,\lambda ,G)$
(which was defined in Remark 5.4). Since
![]() $\lambda $
is a limit of
$\lambda $
is a limit of
![]() $\mathord {<}\lambda $
-strong cardinals,
$\mathord {<}\lambda $
-strong cardinals,
![]() $D(V,\lambda ,G)$
satisfies the statement that every set of reals is Suslin, by a theorem of Woodin which appears as Theorem 9.1 below. Therefore,
$D(V,\lambda ,G)$
satisfies the statement that every set of reals is Suslin, by a theorem of Woodin which appears as Theorem 9.1 below. Therefore,
![]() $A \in \mathrm {ScS}^{D(V,\lambda ,G)} \subseteq \mathrm {ScS}^{V(\mathbb {R}^*_G)} = \mathrm {Hom}^*_G$
, so we have
$A \in \mathrm {ScS}^{D(V,\lambda ,G)} \subseteq \mathrm {ScS}^{V(\mathbb {R}^*_G)} = \mathrm {Hom}^*_G$
, so we have
![]() $A \in \mathrm {Hom}^*_G$
.
$A \in \mathrm {Hom}^*_G$
.
To prove part (3) of the main theorem, we begin with the observation that every set in
![]() $\mathrm {Hom}^*_G$
is
$\mathrm {Hom}^*_G$
is
![]() $\mathord {<}\mathrm {Ord}$
-universally Baire in the symmetric model
$\mathord {<}\mathrm {Ord}$
-universally Baire in the symmetric model
![]() $V(\mathbb {R}^*_G)$
. This follows from the assumption that
$V(\mathbb {R}^*_G)$
. This follows from the assumption that
![]() $\lambda $
is a limit of strong cardinals by a standard argument: a pair of trees
$\lambda $
is a limit of strong cardinals by a standard argument: a pair of trees
![]() $(S,T)$
for a
$(S,T)$
for a
![]() $\mathrm {Hom}^*_G$
set appears
$\mathrm {Hom}^*_G$
set appears
![]() $V[G\mathord {\restriction } \xi ]$
for some
$V[G\mathord {\restriction } \xi ]$
for some
![]() $\xi < \lambda $
, where it is
$\xi < \lambda $
, where it is
![]() $\lambda $
-absolutely complementing. Since
$\lambda $
-absolutely complementing. Since
![]() $\lambda $
is a limit of strong cardinals in V, there is a strong cardinal
$\lambda $
is a limit of strong cardinals in V, there is a strong cardinal
![]() $\kappa < \lambda $
in
$\kappa < \lambda $
in
![]() $V[G\mathord {\restriction } \xi ]$
. For any cardinal
$V[G\mathord {\restriction } \xi ]$
. For any cardinal
![]() $\chi $
, then there is an elementary embedding
$\chi $
, then there is an elementary embedding
![]() $j \colon V \to M$
with critical point
$j \colon V \to M$
with critical point
![]() $\kappa $
and
$\kappa $
and
![]() $j(\kappa )> \chi $
and
$j(\kappa )> \chi $
and
![]() $V_{\chi } \subseteq M$
. Then
$V_{\chi } \subseteq M$
. Then
![]() $(j(S), j(T))$
is a
$(j(S), j(T))$
is a
![]() $\chi $
-complementing pair in
$\chi $
-complementing pair in
![]() $V(\mathbb {R}^{*}_{G})$
, and
$V(\mathbb {R}^{*}_{G})$
, and
![]() $\mathrm {p}[S] = \mathrm {p}[j(S)]$
.
$\mathrm {p}[S] = \mathrm {p}[j(S)]$
.
It then follows that sets in
![]() $\mathrm {Hom}^*_G$
are (fully) universally Baire in
$\mathrm {Hom}^*_G$
are (fully) universally Baire in
![]() $V(\mathbb {R}^*_G)$
, by the following lemma.
$V(\mathbb {R}^*_G)$
, by the following lemma.
Lemma 5.7. Let
![]() $\lambda $
be a cardinal, and let
$\lambda $
be a cardinal, and let
![]() $G \subseteq \mathrm {Col}(\omega ,\mathord {<}\lambda )$
be a V-generic filter. Then in the symmetric model
$G \subseteq \mathrm {Col}(\omega ,\mathord {<}\lambda )$
be a V-generic filter. Then in the symmetric model
![]() $V(\mathbb {R}^*_G)$
, every
$V(\mathbb {R}^*_G)$
, every
![]() $\mathord {<}\mathrm {Ord}$
-universally Baire set of reals is universally Baire. Moreover, this holds locally: for every set Z, there is a cardinal
$\mathord {<}\mathrm {Ord}$
-universally Baire set of reals is universally Baire. Moreover, this holds locally: for every set Z, there is a cardinal
![]() $\eta $
such that every
$\eta $
such that every
![]() $\eta ^{+}$
-absolutely complementing pair of trees on
$\eta ^{+}$
-absolutely complementing pair of trees on
![]() $\omega \times \mathrm {Ord}$
is
$\omega \times \mathrm {Ord}$
is
![]() $\mathrm {Col}(\omega ,Z)$
-absolutely complementing.
$\mathrm {Col}(\omega ,Z)$
-absolutely complementing.
Proof. Fix Z, let
![]() $\eta = \max (\lambda , \left |Z\right |{}^{V[G]})$
, and let
$\eta = \max (\lambda , \left |Z\right |{}^{V[G]})$
, and let
![]() $(S,T)$
be an
$(S,T)$
be an
![]() $\eta ^{+}$
-absolutely complementing pair of trees in
$\eta ^{+}$
-absolutely complementing pair of trees in
![]() $V(\mathbb {R}^*_G)$
. Then, as above, because S and T are subsets of the ground model, a standard homogeneity argument shows that
$V(\mathbb {R}^*_G)$
. Then, as above, because S and T are subsets of the ground model, a standard homogeneity argument shows that
![]() $(S,T) \in V[G \mathord {\restriction } \xi ]$
for some ordinal
$(S,T) \in V[G \mathord {\restriction } \xi ]$
for some ordinal
![]() $\xi < \lambda $
. The pair
$\xi < \lambda $
. The pair
![]() $(S,T)$
is
$(S,T)$
is
![]() $\eta ^{+}$
-absolutely complementing in the model
$\eta ^{+}$
-absolutely complementing in the model
![]() $V[G \mathord {\restriction } \xi ]$
also because this property is downward absolute (since
$V[G \mathord {\restriction } \xi ]$
also because this property is downward absolute (since
![]() $\lambda \leq \eta $
the cardinal successor of
$\lambda \leq \eta $
the cardinal successor of
![]() $\eta $
is the same in all models under consideration).
$\eta $
is the same in all models under consideration).
Since
![]() $\eta \ge \lambda $
, every generic extension of
$\eta \ge \lambda $
, every generic extension of
![]() $V[G]$
by the poset
$V[G]$
by the poset
![]() $\mathrm {Col}(\omega ,\eta )$
is also a generic extension of
$\mathrm {Col}(\omega ,\eta )$
is also a generic extension of
![]() $V[G \mathord {\restriction } \xi ]$
by the poset
$V[G \mathord {\restriction } \xi ]$
by the poset
![]() $\mathrm {Col}(\omega ,\eta )$
. It follows that the pair
$\mathrm {Col}(\omega ,\eta )$
. It follows that the pair
![]() $(S,T)$
is
$(S,T)$
is
![]() $\eta ^{+}$
-absolutely complementing in
$\eta ^{+}$
-absolutely complementing in
![]() $V[G]$
. Since
$V[G]$
. Since
![]() $\eta \ge \left |Z\right |{}^{V[G]}$
, this implies that the pair
$\eta \ge \left |Z\right |{}^{V[G]}$
, this implies that the pair
![]() $(S,T)$
is
$(S,T)$
is
![]() $\mathrm {Col}(\omega , Z)$
-absolutely complementing in
$\mathrm {Col}(\omega , Z)$
-absolutely complementing in
![]() $V[G]$
. This property is downward absolute, so the pair
$V[G]$
. This property is downward absolute, so the pair
![]() $(S,T)$
is
$(S,T)$
is
![]() $\mathrm {Col}(\omega , Z)$
-absolutely complementing in
$\mathrm {Col}(\omega , Z)$
-absolutely complementing in
![]() $V(\mathbb {R}^*_G)$
, as desired.
$V(\mathbb {R}^*_G)$
, as desired.
To prove part (3) of the main theorem, it remains to show that the universal Baireness of
![]() $\mathrm {Hom}^*_G$
sets in
$\mathrm {Hom}^*_G$
sets in
![]() $V(\mathbb {R}^*_G)$
is absorbed by the model
$V(\mathbb {R}^*_G)$
is absorbed by the model
![]() $\mathcal {M}$
via the F predicate. This would follow from Theorem 4.2 if we knew that each member of
$\mathcal {M}$
via the F predicate. This would follow from Theorem 4.2 if we knew that each member of
![]() $\mathrm {Hom}^{*}_{G}$
carried a semiscale coded by a set in
$\mathrm {Hom}^{*}_{G}$
carried a semiscale coded by a set in
![]() $\mathrm {Hom}^{*}_{G}$
. This fact is proved in Section 9, giving the following lemma, finishing the proof of part (3), and part (1), by Remark 5.3.
$\mathrm {Hom}^{*}_{G}$
. This fact is proved in Section 9, giving the following lemma, finishing the proof of part (3), and part (1), by Remark 5.3.
Lemma 5.8 (9.9).
Let
![]() $\lambda $
be a limit of Woodin cardinals and a limit of strong cardinals, and let
$\lambda $
be a limit of Woodin cardinals and a limit of strong cardinals, and let
![]() $G \subseteq \mathrm {Col}(\omega ,\mathord {<}\lambda )$
be a V-generic filter. Then every set of reals in
$G \subseteq \mathrm {Col}(\omega ,\mathord {<}\lambda )$
be a V-generic filter. Then every set of reals in
![]() $\mathrm {Hom}^*_G$
is universally Baire in
$\mathrm {Hom}^*_G$
is universally Baire in
![]() $L^F(\mathbb {R}^*_G, \mathrm {Hom}^*_G)^{V(\mathbb {R}^*_G)}$
.
$L^F(\mathbb {R}^*_G, \mathrm {Hom}^*_G)^{V(\mathbb {R}^*_G)}$
.
For part (4) of the main theorem, parts (2) and (3), along with Theorem 4.3 (with
![]() $\Gamma = \mathrm {Hom}^{*}_{G}$
) imply that the restriction of F to
$\Gamma = \mathrm {Hom}^{*}_{G}$
) imply that the restriction of F to
![]() $\mathcal {M}$
is the same as the predicate F defined in
$\mathcal {M}$
is the same as the predicate F defined in
![]() $\mathcal {M}$
. As in Corollary 4.4, it follows that
$\mathcal {M}$
. As in Corollary 4.4, it follows that
![]() $\mathcal {M}$
sees its own construction (in particular,
$\mathcal {M}$
sees its own construction (in particular,
![]() $\mathcal {M}= L^{F}(\mathbb {R}, \mathcal {P}(\mathbb {R}))^{\mathcal {M}}$
), so every element of
$\mathcal {M}= L^{F}(\mathbb {R}, \mathcal {P}(\mathbb {R}))^{\mathcal {M}}$
), so every element of
![]() $\mathcal {M}$
is ordinal-definable in
$\mathcal {M}$
is ordinal-definable in
![]() $\mathcal {M}$
from a member of
$\mathcal {M}$
from a member of
![]() $\mathcal {P}(\mathbb {R})^{\mathcal {M}}$
.
$\mathcal {P}(\mathbb {R})^{\mathcal {M}}$
.
For the last part of the theorem (the minimality property of
![]() $\mathcal {M}$
), note that if
$\mathcal {M}$
), note that if
![]() $\mathcal {M}^{\prime } \subseteq V(\mathbb {R}^{*}_{G})$
contains
$\mathcal {M}^{\prime } \subseteq V(\mathbb {R}^{*}_{G})$
contains
![]() $\mathrm {Hom}^{*}_{G}$
and satisfies the statement that all sets of reals are universally Baire (and thus Suslin), then, since
$\mathrm {Hom}^{*}_{G}$
and satisfies the statement that all sets of reals are universally Baire (and thus Suslin), then, since
![]() $\mathrm {Hom}^{*}_{G} = \mathrm {ScS}^{V(\mathbb {R}^{*}_{G})},\ \mathrm {Hom}^{*}_{G} = \mathcal {P}(\mathbb {R})^{\mathcal {M}^{\prime }}$
, and in particular
$\mathrm {Hom}^{*}_{G} = \mathrm {ScS}^{V(\mathbb {R}^{*}_{G})},\ \mathrm {Hom}^{*}_{G} = \mathcal {P}(\mathbb {R})^{\mathcal {M}^{\prime }}$
, and in particular
![]() $\mathrm {Hom}^{*}_{G}$
, is an element of
$\mathrm {Hom}^{*}_{G}$
, is an element of
![]() $\mathcal {M}^{\prime }$
. It follows from Lemma 4.3 then that
$\mathcal {M}^{\prime }$
. It follows from Lemma 4.3 then that
![]() $\mathcal {M} \subseteq \mathcal {M}^{\prime }$
.
$\mathcal {M} \subseteq \mathcal {M}^{\prime }$
.
To finish the proof of the main theorem, then, it remains only to prove Lemmas 8.1 and 9.9, and Theorem 9.1.
6
 $\mathbb {R}$
-genericity iterations
$\mathbb {R}$
-genericity iterations
As in Steel’s stationary-tower-free proof [Reference Steel, Gao, Jackson and Zhang22] of
![]() $\Sigma ^2_1$
reflection for the model
$\Sigma ^2_1$
reflection for the model
![]() $L(\mathbb {R}^*_G, \mathrm {Hom}^*_G)$
, our proof of
$L(\mathbb {R}^*_G, \mathrm {Hom}^*_G)$
, our proof of
![]() $\Sigma ^2_1$
reflection for the model
$\Sigma ^2_1$
reflection for the model
![]() $\mathcal {M}$
of the main theorem will make fundamental use of the genericity iterations of Neeman [Reference Neeman17], repeated
$\mathcal {M}$
of the main theorem will make fundamental use of the genericity iterations of Neeman [Reference Neeman17], repeated
![]() $\omega $
many times to produce an
$\omega $
many times to produce an
![]() $\mathbb {R}$
-genericity iteration. We refer the reader also to Neeman [Reference Neeman, Foreman and Kanamori18] for a thorough account of the use of
$\mathbb {R}$
-genericity iteration. We refer the reader also to Neeman [Reference Neeman, Foreman and Kanamori18] for a thorough account of the use of
![]() $\mathbb {R}$
-genericity iterations to prove
$\mathbb {R}$
-genericity iterations to prove
![]() $\mathsf {AD}$
in
$\mathsf {AD}$
in
![]() $L(\mathbb {R}^*_G)$
by a similar reflection argument.
$L(\mathbb {R}^*_G)$
by a similar reflection argument.
The definitions we give below are more or less standard; we include them here to set out the notation that we will use in the rest of the paper. In the following definition, ‘sufficient fragment’ can be taken to mean sufficiently large for the definition (e.g., Woodin cardinals and generic extensions) to make sense. In practice,
![]() $P_{0}$
will be the transitive collapse of a suitably large rank initial segment of the universe.
$P_{0}$
will be the transitive collapse of a suitably large rank initial segment of the universe.
Definition 6.1. Let
![]() $P_0$
be a model of a sufficient fragment of
$P_0$
be a model of a sufficient fragment of
![]() $\mathsf {ZFC}$
, and let
$\mathsf {ZFC}$
, and let
![]() $\bar {\lambda }$
be a limit of Woodin cardinals of
$\bar {\lambda }$
be a limit of Woodin cardinals of
![]() $P_0$
. An
$P_0$
. An
![]() $\mathbb {R}$
-genericity iteration of
$\mathbb {R}$
-genericity iteration of
![]() $P_0\ at \ \bar {\lambda }$
is a sequence
$P_0\ at \ \bar {\lambda }$
is a sequence
existing in a generic extension of V by
![]() $\mathrm {Col}(\omega ,\mathbb {R})$
, such that
$\mathrm {Col}(\omega ,\mathbb {R})$
, such that
-
1.
 $P_j$
is in V, for each
$P_j$
is in V, for each
 $j < \omega $
,
$j < \omega $
, -
2.
 $i_{jk}$
is an elementary embedding from
$i_{jk}$
is an elementary embedding from
 $P_j$
to
$P_j$
to
 $P_k$
, for all
$P_k$
, for all
 $j \leq k \leq \omega $
,
$j \leq k \leq \omega $
, -
3.
 $i_{jk}$
is an element of V, whenever
$i_{jk}$
is an element of V, whenever
 $j \leq k < \omega $
,
$j \leq k < \omega $
, -
4.
 $x_\ell \in \mathbb {R}^{V}$
, for all
$x_\ell \in \mathbb {R}^{V}$
, for all
 $\ell < \omega $
,
$\ell < \omega $
, -
5. each
 $\delta _{\ell }$
is a Woodin cardinal below
$\delta _{\ell }$
is a Woodin cardinal below
 $i_{0,\ell }(\bar {\lambda })$
in
$i_{0,\ell }(\bar {\lambda })$
in
 $P_{\ell }$
,
$P_{\ell }$
, -
6. for all
 $\ell < \omega , \ g_{\ell } \in V$
is a
$\ell < \omega , \ g_{\ell } \in V$
is a
 $P_{\ell +1}$
-generic filter for the poset
$P_{\ell +1}$
-generic filter for the poset
 $\mathrm {Col}(\omega ,i_{\ell ,\ell +1}(\delta _\ell ))$
such that
$\mathrm {Col}(\omega ,i_{\ell ,\ell +1}(\delta _\ell ))$
such that
 $x_\ell \in P_{\ell +1}[g_{\ell }]$
,
$x_\ell \in P_{\ell +1}[g_{\ell }]$
, -
7.
 $i_{kp} \circ i_{jk} = i_{jp}$
whenever
$i_{kp} \circ i_{jk} = i_{jp}$
whenever
 $j \le k \le p \le \omega $
,
$j \le k \le p \le \omega $
, -
8.
 $P_\omega $
and the maps
$P_\omega $
and the maps
 $i_{j,\omega }$
(
$i_{j,\omega }$
(
 $j < \omega $
) are obtained as direct limits from the maps
$j < \omega $
) are obtained as direct limits from the maps
 $i_{jk}$
(
$i_{jk}$
(
 $j \leq k < \omega $
),
$j \leq k < \omega $
), -
9.
 $i_{j,j+1}(\delta _j) < \delta _{j+1}$
for all
$i_{j,j+1}(\delta _j) < \delta _{j+1}$
for all
 $j < \omega $
,
$j < \omega $
, -
10. for all
 $j < k < \omega $
, the map
$j < k < \omega $
, the map
 $i_{j+1,k+1}$
has critical point above
$i_{j+1,k+1}$
has critical point above
 $i_{j,j+1}(\delta _j)$
,
$i_{j,j+1}(\delta _j)$
, -
11.
 $\{x_j : x < \omega \} = \mathbb {R}^V$
,
$\{x_j : x < \omega \} = \mathbb {R}^V$
, -
12.
 $i_{0,\omega }(\bar {\lambda }) = \sup \{i_{j,\omega }(\delta _j) : j < \omega \}$
and
$i_{0,\omega }(\bar {\lambda }) = \sup \{i_{j,\omega }(\delta _j) : j < \omega \}$
and -
13. there is a
 $P_\omega $
-generic filter
$P_\omega $
-generic filter
 $g \subseteq \mathrm {Col}(\omega ,\mathord {<}i_{0,\omega }(\bar {\lambda }))$
such that
$g \subseteq \mathrm {Col}(\omega ,\mathord {<}i_{0,\omega }(\bar {\lambda }))$
such that  $$\begin{align*}\mathbb{R}^V = \bigcup\{ \mathbb{R} \cap P_{\omega}[g \mathord{\restriction} \xi] : \xi < i_{0,\omega}(\bar{\lambda})\}.\end{align*}$$
$$\begin{align*}\mathbb{R}^V = \bigcup\{ \mathbb{R} \cap P_{\omega}[g \mathord{\restriction} \xi] : \xi < i_{0,\omega}(\bar{\lambda})\}.\end{align*}$$
Parallel to the notation in Section 5, in the context of item (13) above, we write
![]() $P_{\omega }(\mathbb {R}^{V})$
for
$P_{\omega }(\mathbb {R}^{V})$
for
By item (10), each embedding
![]() $i_{j+1,k+1}$
extends to an elementary embedding from
$i_{j+1,k+1}$
extends to an elementary embedding from
![]() $P_{j+1}[g_j]$
to
$P_{j+1}[g_j]$
to
![]() $P_{k+1}[g_j]$
, which we call
$P_{k+1}[g_j]$
, which we call
![]() $i_{j+1,k+1}^*$
.
$i_{j+1,k+1}^*$
.
Remark 6.2. Each partial order
![]() $\mathrm {Col}(\omega ,i_{\ell ,\ell +1}(\delta _\ell ))$
as in item (6) above is forcing-equivalent to the corresponding partial order
$\mathrm {Col}(\omega ,i_{\ell ,\ell +1}(\delta _\ell ))$
as in item (6) above is forcing-equivalent to the corresponding partial order
in the case
![]() $\ell> 0$
, and
$\ell> 0$
, and
![]() $\mathrm {Col}(\omega \leq i_{01}(\delta _{0}))$
in the case
$\mathrm {Col}(\omega \leq i_{01}(\delta _{0}))$
in the case
![]() $\ell = 0$
. In practice (i.e., in the proof of Lemma 6.6), the generic filter g in item (13) is the union of the images of the filters
$\ell = 0$
. In practice (i.e., in the proof of Lemma 6.6), the generic filter g in item (13) is the union of the images of the filters
![]() $g_{\ell }$
under isomorphisms witnessing these forcing-equivalences (via bookkeeping that we leave to the reader).
$g_{\ell }$
under isomorphisms witnessing these forcing-equivalences (via bookkeeping that we leave to the reader).
To ensure that the symmetric model
![]() $P_\omega (\mathbb {R}^V)$
resembles V in some sense, we will use
$P_\omega (\mathbb {R}^V)$
resembles V in some sense, we will use
![]() $\mathbb {R}$
-genericity iterations of countable hulls
$\mathbb {R}$
-genericity iterations of countable hulls
![]() $P_0$
of rank initial segments of V where the iteration maps factor into the uncollapse map of the hull. The notation below suppresses
$P_0$
of rank initial segments of V where the iteration maps factor into the uncollapse map of the hull. The notation below suppresses
![]() $\gamma $
, which is implicitly assumed to be associated with the map
$\gamma $
, which is implicitly assumed to be associated with the map
![]() $\pi _{0}$
.
$\pi _{0}$
.
Definition 6.3. Let
![]() $\lambda $
be a limit of Woodin cardinals, let
$\lambda $
be a limit of Woodin cardinals, let
![]() $\gamma> \lambda $
be an ordinal, and let
$\gamma> \lambda $
be an ordinal, and let
![]() $\pi _0 \colon P_0 \to V_{\gamma }$
be an elementary embedding of a countable transitive set
$\pi _0 \colon P_0 \to V_{\gamma }$
be an elementary embedding of a countable transitive set
![]() $P_0$
into V such that
$P_0$
into V such that
![]() $\lambda \in \operatorname {\mathrm {ran}}(\pi _0)$
.
$\lambda \in \operatorname {\mathrm {ran}}(\pi _0)$
.
An
![]() $\mathbb {R}$
-genericity iteration of
$\mathbb {R}$
-genericity iteration of
![]() $P_0$
at
$P_0$
at
![]() $\pi _0^{-1}(\lambda )$
, as in Definition 6.1, is
$\pi _0^{-1}(\lambda )$
, as in Definition 6.1, is
![]() $\pi _0$
-realizable if there are elementary embeddings
$\pi _0$
-realizable if there are elementary embeddings
![]() $\pi _j : P_j \to V_{\gamma }$
for
$\pi _j : P_j \to V_{\gamma }$
for
![]() $j \le \omega $
that commute with the iteration maps, meaning that
$j \le \omega $
that commute with the iteration maps, meaning that
![]() $\pi _k \circ i_{jk} = \pi _j$
for
$\pi _k \circ i_{jk} = \pi _j$
for
![]() $j \le k \le \omega $
, and such that
$j \le k \le \omega $
, and such that
![]() $\pi _j \in V$
for all
$\pi _j \in V$
for all
![]() $j < \omega $
.
$j < \omega $
.
For simplicity, we will sometimes abuse notation by referring to a
![]() $\pi _0$
-realizable genericity iteration of
$\pi _0$
-realizable genericity iteration of
![]() $P_0$
at
$P_0$
at
![]() $\pi _0^{-1}(\lambda )$
as a
$\pi _0^{-1}(\lambda )$
as a
![]() $\pi _0$
-realizable genericity iteration of
$\pi _0$
-realizable genericity iteration of
![]() $P_0$
at
$P_0$
at
![]() $\lambda $
; this should not cause any confusion because
$\lambda $
; this should not cause any confusion because
![]() $\lambda $
is a limit of Woodin cardinals and
$\lambda $
is a limit of Woodin cardinals and
![]() $\pi _0^{-1}(\lambda )$
is a countable ordinal.
$\pi _0^{-1}(\lambda )$
is a countable ordinal.
Remark 6.4. If C is a
![]() $\lambda $
-universally Baire set of reals,
$\lambda $
-universally Baire set of reals,
![]() $\gamma> \lambda $
is a limit ordinal,
$\gamma> \lambda $
is a limit ordinal,
![]() $P_{0}$
is a countable transitive set and
$P_{0}$
is a countable transitive set and
![]() $\pi _0 \colon P_0 \to V_{\gamma }$
is an elementary embedding with
$\pi _0 \colon P_0 \to V_{\gamma }$
is an elementary embedding with
![]() $(C,\lambda ) \in \operatorname {\mathrm {ran}}(\pi _0)$
, then for every
$(C,\lambda ) \in \operatorname {\mathrm {ran}}(\pi _0)$
, then for every
![]() $\pi _0$
-realizable genericity iteration
$\pi _0$
-realizable genericity iteration
![]() $P_0 \to P_\omega $
at
$P_0 \to P_\omega $
at
![]() $\lambda $
, we have
$\lambda $
, we have
![]() $C \in P_\omega (\mathbb {R}^V)$
, and in particular, C is equal to
$C \in P_\omega (\mathbb {R}^V)$
, and in particular, C is equal to
![]() $\pi _\omega ^{-1}(C)^{P_\omega (\mathbb {R}^V)}$
, the canonical expansion of
$\pi _\omega ^{-1}(C)^{P_\omega (\mathbb {R}^V)}$
, the canonical expansion of
![]() $\pi _\omega ^{-1}(C)$
in
$\pi _\omega ^{-1}(C)$
in
![]() $P_\omega (\mathbb {R}^V)$
. To see this, note that
$P_\omega (\mathbb {R}^V)$
. To see this, note that
![]() $\operatorname {\mathrm {ran}}(\pi _0)$
contains a
$\operatorname {\mathrm {ran}}(\pi _0)$
contains a
![]() $\lambda $
-absolutely complementing pair of trees
$\lambda $
-absolutely complementing pair of trees
![]() $(S,T)$
for C. Then
$(S,T)$
for C. Then
![]() $\mathrm {p}[\pi _\omega ^{-1}(S)] \subseteq \mathrm {p}[S] = C$
and
$\mathrm {p}[\pi _\omega ^{-1}(S)] \subseteq \mathrm {p}[S] = C$
and
![]() $\mathrm {p}[\pi _\omega ^{-1}(T)] \subseteq \mathrm {p}[T]$
, so the canonical expansion of
$\mathrm {p}[\pi _\omega ^{-1}(T)] \subseteq \mathrm {p}[T]$
, so the canonical expansion of
![]() $\pi _\omega ^{-1}(C)$
in
$\pi _\omega ^{-1}(C)$
in
![]() $P_\omega (\mathbb {R}^V)$
is equal to C.
$P_\omega (\mathbb {R}^V)$
is equal to C.
Remark 6.5. The notion of
![]() $\mathbb {R}$
-genericity iteration given by Definition 6.1 is weaker than the usual one because it does not require the elementary embeddings
$\mathbb {R}$
-genericity iteration given by Definition 6.1 is weaker than the usual one because it does not require the elementary embeddings
![]() $i_{jk} \colon P_j \to P_k$
to be iteration maps. (We could have called them something like ‘
$i_{jk} \colon P_j \to P_k$
to be iteration maps. (We could have called them something like ‘
![]() $\mathbb {R}$
-genericity systems’ instead.) We do it this way so that the reader unfamiliar with iteration trees can take the following lemma (which is implicit in Steel [Reference Steel, Gao, Jackson and Zhang22]) as a black box; its proof is the only place where iteration trees will appear in this paper.
$\mathbb {R}$
-genericity systems’ instead.) We do it this way so that the reader unfamiliar with iteration trees can take the following lemma (which is implicit in Steel [Reference Steel, Gao, Jackson and Zhang22]) as a black box; its proof is the only place where iteration trees will appear in this paper.
The conditions on
![]() $\gamma $
in the hypotheses of Lemma 6.6 are chosen to make
$\gamma $
in the hypotheses of Lemma 6.6 are chosen to make
![]() $V_{\gamma }$
satisfy the theory in Definition 1.1 of [Reference Martin and Steel13], with respect to
$V_{\gamma }$
satisfy the theory in Definition 1.1 of [Reference Martin and Steel13], with respect to
![]() $\lambda $
. Recall from Remark 5.5 that
$\lambda $
. Recall from Remark 5.5 that
![]() $\mathrm {Hom}_{\mathord {<}\lambda } = \mathrm {uB}_{\lambda }$
when
$\mathrm {Hom}_{\mathord {<}\lambda } = \mathrm {uB}_{\lambda }$
when
![]() $\lambda $
is a limit of Woodin cardinals. Remark 6.4 shows that the expression
$\lambda $
is a limit of Woodin cardinals. Remark 6.4 shows that the expression
![]() $P_\omega (\mathbb {R}^V) \models \psi [C,x]$
in the statement of the lemma makes sense (i.e., that C is in
$P_\omega (\mathbb {R}^V) \models \psi [C,x]$
in the statement of the lemma makes sense (i.e., that C is in
![]() $P_{\omega }(\mathbb {R}^{V})$
).
$P_{\omega }(\mathbb {R}^{V})$
).
Lemma 6.6. Let
![]() $\lambda $
be a limit of Woodin cardinals, and let C be a
$\lambda $
be a limit of Woodin cardinals, and let C be a
![]() $\lambda $
-universally Baire set of reals. Let
$\lambda $
-universally Baire set of reals. Let
![]() $P_{0}$
be a countable transitive set, and let
$P_{0}$
be a countable transitive set, and let
![]() $\gamma $
be a limit ordinal of cofinality greater than
$\gamma $
be a limit ordinal of cofinality greater than
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $\pi _0 \colon P_0 \to V_{\gamma }$
be an elementary embedding with
$\pi _0 \colon P_0 \to V_{\gamma }$
be an elementary embedding with
![]() $(C,\lambda ) \in \operatorname {\mathrm {ran}}(\pi _0)$
. Suppose that A is a set of reals in V and that there is a binary formula
$(C,\lambda ) \in \operatorname {\mathrm {ran}}(\pi _0)$
. Suppose that A is a set of reals in V and that there is a binary formula
![]() $\psi $
such that for every
$\psi $
such that for every
![]() $\pi _0$
-realizable
$\pi _0$
-realizable
![]() $\mathbb {R}$
-genericity iteration
$\mathbb {R}$
-genericity iteration
![]() $P_0 \to P_\omega $
at
$P_0 \to P_\omega $
at
![]() $\lambda $
in
$\lambda $
in
![]() $V^{\mathrm {Col}(\omega ,\mathbb {R})}$
and every real
$V^{\mathrm {Col}(\omega ,\mathbb {R})}$
and every real
![]() $x \in V$
, we have
$x \in V$
, we have
Then
![]() $A \in \mathrm {Hom}_{\mathord {<}\lambda }$
.
$A \in \mathrm {Hom}_{\mathord {<}\lambda }$
.
Proof. By the wellfoundedness of the Wadge hierarchy on homogeneously Suslin sets (see Theorem 3.3.5 of [Reference Larson10] and the discussion before it), there is minimal
![]() $\kappa < \lambda $
such that every
$\kappa < \lambda $
such that every
![]() $\kappa $
-homogeneously Suslin set of reals is
$\kappa $
-homogeneously Suslin set of reals is
![]() $\mathord {<}\lambda $
-homogeneously Suslin. By the elementarity of
$\mathord {<}\lambda $
-homogeneously Suslin. By the elementarity of
![]() $\pi $
, we have
$\pi $
, we have
![]() $\kappa \in \operatorname {\mathrm {ran}}(\pi _0)$
and
$\kappa \in \operatorname {\mathrm {ran}}(\pi _0)$
and
![]() $(S,T) \in \operatorname {\mathrm {ran}}(\pi _0)$
for some
$(S,T) \in \operatorname {\mathrm {ran}}(\pi _0)$
for some
![]() $\lambda $
-absolutely complementing pair of trees
$\lambda $
-absolutely complementing pair of trees
![]() $(S,T)$
for C. Define
$(S,T)$
for C. Define
![]() $(\bar {\lambda },\bar {\kappa },\bar {S},\bar {T}) = \pi _0^{-1}(\lambda ,\kappa ,S,T)$
. Let
$(\bar {\lambda },\bar {\kappa },\bar {S},\bar {T}) = \pi _0^{-1}(\lambda ,\kappa ,S,T)$
. Let
![]() $\delta _0$
denote the least Woodin cardinal of
$\delta _0$
denote the least Woodin cardinal of
![]() $P_0$
above
$P_0$
above
![]() $\bar {\kappa }$
.
$\bar {\kappa }$
.
Let W denote the set of all (reals coding) ordered pairs
![]() $(\mathcal {T},b)$
such that
$(\mathcal {T},b)$
such that
-
•
 $\mathcal {T}$
is a
$\mathcal {T}$
is a
 $2^\omega $
-closed iteration tree on
$2^\omega $
-closed iteration tree on
 $P_0$
of length
$P_0$
of length
 $\omega $
(meaning that each extender produces a
$\omega $
(meaning that each extender produces a
 $2^{\omega }$
-closed ultrapower when applied to the model from which it is chosen),
$2^{\omega }$
-closed ultrapower when applied to the model from which it is chosen), -
•
 $\mathcal {T}$
is above
$\mathcal {T}$
is above
 $\bar {\kappa }$
and based on
$\bar {\kappa }$
and based on
 $\delta _0$
(meaning that each extender chosen has critical point above
$\delta _0$
(meaning that each extender chosen has critical point above
 $\bar {\kappa }$
and von Neumann rank below the corresponding image of
$\bar {\kappa }$
and von Neumann rank below the corresponding image of
 $\delta _{0}$
),
$\delta _{0}$
), -
• b is a cofinal branch of
 $\mathcal {T}$
, and
$\mathcal {T}$
, and -
• the model
 $\mathcal {M}_b^{\pi _0\mathcal {T}}$
is wellfounded, where
$\mathcal {M}_b^{\pi _0\mathcal {T}}$
is wellfounded, where
 $\pi _0\mathcal {T}$
is the lifted tree on
$\pi _0\mathcal {T}$
is the lifted tree on
 $V_{\gamma }$
.
$V_{\gamma }$
.
As shown by Martin and Steel [Reference Martin and Steel13, p. 27], the condition that the model
![]() $\mathcal {M}_b^{\pi _0\mathcal {T}}$
is wellfounded implies that the branch b is
$\mathcal {M}_b^{\pi _0\mathcal {T}}$
is wellfounded implies that the branch b is
![]() $\pi _0$
-realizable (meaning that the branch embedding
$\pi _0$
-realizable (meaning that the branch embedding
![]() $i^{\mathcal {T}}_b$
factors into
$i^{\mathcal {T}}_b$
factors into
![]() $\pi _0$
), which in turn implies that the model
$\pi _0$
), which in turn implies that the model
![]() $\mathcal {M}_b^{\mathcal {T}}$
is wellfounded.
$\mathcal {M}_b^{\mathcal {T}}$
is wellfounded.
By a result of K. Windszus (see Steel [Reference Steel, Gao, Jackson and Zhang22, Lemma 1.1]) the set W is
![]() $\kappa $
-homogeneously Suslin and therefore
$\kappa $
-homogeneously Suslin and therefore
![]() $\mathord {<}\lambda $
-homogeneously Suslin by our choice of
$\mathord {<}\lambda $
-homogeneously Suslin by our choice of
![]() $\kappa $
. (We added the condition that
$\kappa $
. (We added the condition that
![]() $\mathcal {T}$
is based on
$\mathcal {T}$
is based on
![]() $\delta _0$
, which is harmless and convenient.) Note that essentially all of the complexity of W comes from condition that
$\delta _0$
, which is harmless and convenient.) Note that essentially all of the complexity of W comes from condition that
![]() $\mathcal {M}_{b}^{\pi _0\mathcal {T}}$
is wellfounded; the other conditions are arithmetic.
$\mathcal {M}_{b}^{\pi _0\mathcal {T}}$
is wellfounded; the other conditions are arithmetic.
Next, we show (following Steel [Reference Steel, Gao, Jackson and Zhang22, Claim 2 on p. 7]) that the following statements are equivalent, for all
![]() $x \in \mathbb {R}$
:
$x \in \mathbb {R}$
:
-
1.
 $x \in A$
.
$x \in A$
. -
2. There exist a pair
 $(\mathcal {T},b) \in W$
and an
$(\mathcal {T},b) \in W$
and an
 $\mathcal {M}^{\mathcal {T}}_b$
-generic filter such that
$\mathcal {M}^{\mathcal {T}}_b$
-generic filter such that $$\begin{align*}g \subseteq \mathrm{Col}(\omega,i^{\mathcal{T}}_b(\delta_0))\end{align*}$$
$$\begin{align*}g \subseteq \mathrm{Col}(\omega,i^{\mathcal{T}}_b(\delta_0))\end{align*}$$
 $x \in \mathcal {M}^{\mathcal {T}}_b[g]$
and
$x \in \mathcal {M}^{\mathcal {T}}_b[g]$
and
 $\psi \big [\mathrm {p}[i^{\mathcal {T}}_b(\bar {S})],x\big ]$
holds in the symmetric extension of
$\psi \big [\mathrm {p}[i^{\mathcal {T}}_b(\bar {S})],x\big ]$
holds in the symmetric extension of
 $\mathcal {M}^{\mathcal {T}}_b[g]$
at its limit
$\mathcal {M}^{\mathcal {T}}_b[g]$
at its limit
 $i^{\mathcal {T}}_b(\bar {\lambda })$
of Woodin cardinals. (It does not matter which symmetric extension, by the homogeneity of the Levy collapse forcing.)
$i^{\mathcal {T}}_b(\bar {\lambda })$
of Woodin cardinals. (It does not matter which symmetric extension, by the homogeneity of the Levy collapse forcing.)
The two directions of the equivalence of (1) and (2) can be proved by constructing a suitable
![]() $\pi _{0}$
-realizable
$\pi _{0}$
-realizable
![]() $\mathbb {R}$
-genericity iteration of
$\mathbb {R}$
-genericity iteration of
![]() $P_{0}$
at
$P_{0}$
at
![]() $\lambda $
. We prove the forward direction first and then note the changes needed for the reverse direction.
$\lambda $
. We prove the forward direction first and then note the changes needed for the reverse direction.
Fix
![]() $x \in \mathbb {R}$
(at the end of the proof, we will assume in addition that x is in A), and note that because
$x \in \mathbb {R}$
(at the end of the proof, we will assume in addition that x is in A), and note that because
![]() $\delta _0$
is a Woodin cardinal of
$\delta _0$
is a Woodin cardinal of
![]() $P_0$
, by Theorem 7.16 of Neeman [Reference Neeman, Foreman and Kanamori18], there is a
$P_0$
, by Theorem 7.16 of Neeman [Reference Neeman, Foreman and Kanamori18], there is a
![]() $2^\omega $
-closed iteration tree
$2^\omega $
-closed iteration tree
![]() $\mathcal {T}$
on
$\mathcal {T}$
on
![]() $P_0$
that is above
$P_0$
that is above
![]() $\bar {\kappa }$
, based on
$\bar {\kappa }$
, based on
![]() $\delta _0$
, of length
$\delta _0$
, of length
![]() $\omega $
, such that for every cofinal wellfounded branch b of
$\omega $
, such that for every cofinal wellfounded branch b of
![]() $\mathcal {T}$
, there is a
$\mathcal {T}$
, there is a
![]() $\mathcal {M}^{\mathcal {T}}_b$
-generic filter
$\mathcal {M}^{\mathcal {T}}_b$
-generic filter
![]() $g \subseteq \mathrm {Col}(\omega ,i^{\mathcal {T}}_b(\delta _0))$
such that
$g \subseteq \mathrm {Col}(\omega ,i^{\mathcal {T}}_b(\delta _0))$
such that
![]() $x \in \mathcal {M}^{\mathcal {T}}_b[g]$
. By Martin and Steel [Reference Martin and Steel13, Corollary 5.7], the
$x \in \mathcal {M}^{\mathcal {T}}_b[g]$
. By Martin and Steel [Reference Martin and Steel13, Corollary 5.7], the
![]() $2^\omega $
-closed iteration tree
$2^\omega $
-closed iteration tree
![]() $\pi _0\mathcal {T}$
on
$\pi _0\mathcal {T}$
on
![]() $V_{\gamma }$
has a cofinal wellfounded branch b. For such a branch b, the pair
$V_{\gamma }$
has a cofinal wellfounded branch b. For such a branch b, the pair
![]() $(\mathcal {T},b)$
is in W, and there is a
$(\mathcal {T},b)$
is in W, and there is a
![]() $\mathcal {M}^{\mathcal {T}}_b$
-generic filter
$\mathcal {M}^{\mathcal {T}}_b$
-generic filter
![]() $g \subseteq \mathrm {Col}(\omega ,i^{\mathcal {T}}_b(\delta _0))$
such that
$g \subseteq \mathrm {Col}(\omega ,i^{\mathcal {T}}_b(\delta _0))$
such that
![]() $x \in \mathcal {M}^{\mathcal {T}}_b[g]$
.
$x \in \mathcal {M}^{\mathcal {T}}_b[g]$
.
Now let
![]() $x_0 = x$
, and let
$x_0 = x$
, and let
![]() $\mathcal {T}_0,\ b_0$
and
$\mathcal {T}_0,\ b_0$
and
![]() $g_0$
be such that
$g_0$
be such that
![]() $(\mathcal {T}_0,b_0) \in W, \ g_0 \subseteq \mathrm {Col}(\omega ,i^{\mathcal {T}}_b(\delta _0))$
is an
$(\mathcal {T}_0,b_0) \in W, \ g_0 \subseteq \mathrm {Col}(\omega ,i^{\mathcal {T}}_b(\delta _0))$
is an
![]() $\mathcal {M}^{\mathcal {T}_0}_{b_0}$
-generic filter, and
$\mathcal {M}^{\mathcal {T}_0}_{b_0}$
-generic filter, and
![]() $x \in \mathcal {M}^{\mathcal {T}_0}_{b_0}[g_0]$
. (The previous paragraph shows that such
$x \in \mathcal {M}^{\mathcal {T}_0}_{b_0}[g_0]$
. (The previous paragraph shows that such
![]() $\mathcal {T}_0,\ b_0$
and
$\mathcal {T}_0,\ b_0$
and
![]() $g_0$
exist.) Let
$g_0$
exist.) Let
![]() $P_1 = \mathcal {M}^{\mathcal {T}_0}_{b_0}$
, and let
$P_1 = \mathcal {M}^{\mathcal {T}_0}_{b_0}$
, and let
![]() $i_{0,1} = i^{\mathcal {T}_{0}}_{b_{0}}$
be the branch embedding from
$i_{0,1} = i^{\mathcal {T}_{0}}_{b_{0}}$
be the branch embedding from
![]() $P_{0}$
to
$P_{0}$
to
![]() $P_{1}$
. As noted above, the condition that
$P_{1}$
. As noted above, the condition that
![]() $\mathcal {M}_{b_0}^{\pi _0\mathcal {T}_0}$
is wellfounded implies that the branch
$\mathcal {M}_{b_0}^{\pi _0\mathcal {T}_0}$
is wellfounded implies that the branch
![]() $b_0$
is
$b_0$
is
![]() $\pi _0$
-realizable, meaning that there is an elementary embedding
$\pi _0$
-realizable, meaning that there is an elementary embedding
![]() $\pi _1 : P_1 \to V_{\gamma }$
such that
$\pi _1 : P_1 \to V_{\gamma }$
such that
![]() $\pi _1 \circ i_{0,1} = \pi _0$
.
$\pi _1 \circ i_{0,1} = \pi _0$
.
Now with the model
![]() $P_1$
in place of the model
$P_1$
in place of the model
![]() $P_0$
, the map
$P_0$
, the map
![]() $\pi _1$
in place of the map
$\pi _1$
in place of the map
![]() $\pi _0$
, a Woodin cardinal
$\pi _0$
, a Woodin cardinal
![]() $\delta _1$
of
$\delta _1$
of
![]() $P_1$
such that
$P_1$
such that
![]() $i_{0,1}(\delta _0) < \delta _1 < i_{0,1}(\bar {\lambda })$
in place of
$i_{0,1}(\delta _0) < \delta _1 < i_{0,1}(\bar {\lambda })$
in place of
![]() $\delta _0$
, and an arbitrary real
$\delta _0$
, and an arbitrary real
![]() $x_1$
, we can repeat the process above, applying the Neeman and Martin–Steel theorems again to get an iteration tree
$x_1$
, we can repeat the process above, applying the Neeman and Martin–Steel theorems again to get an iteration tree
![]() $\mathcal {T}_1$
on
$\mathcal {T}_1$
on
![]() $P_1$
of length
$P_1$
of length
![]() $\omega $
, above
$\omega $
, above
![]() $i_{0,1}(\delta _0)$
and based on
$i_{0,1}(\delta _0)$
and based on
![]() $\delta _1$
, a
$\delta _1$
, a
![]() $\pi _1$
-realizable branch
$\pi _1$
-realizable branch
![]() $b_1$
of
$b_1$
of
![]() $\mathcal {T}_1$
, and an
$\mathcal {T}_1$
, and an
![]() $\mathcal {M}^{\mathcal {T}_1}_{b_1}$
-generic filter
$\mathcal {M}^{\mathcal {T}_1}_{b_1}$
-generic filter
![]() $g_1 \subseteq \mathrm {Col}(\omega , i^{\mathcal {T}_1}_{b_1}(\delta _1))$
such that
$g_1 \subseteq \mathrm {Col}(\omega , i^{\mathcal {T}_1}_{b_1}(\delta _1))$
such that
![]() $x_1 \in \mathcal {M}^{\mathcal {T}_1}_{b_1}[g_1]$
.
$x_1 \in \mathcal {M}^{\mathcal {T}_1}_{b_1}[g_1]$
.
We can repeat this process for
![]() $\omega $
many stages. (Note that, for the purposes of showing the equivalence of (1) and (2), at a stage
$\omega $
many stages. (Note that, for the purposes of showing the equivalence of (1) and (2), at a stage
![]() $j>0$
, it suffices to use a
$j>0$
, it suffices to use a
![]() $\pi _j$
-realizable branch of
$\pi _j$
-realizable branch of
![]() $\mathcal {T}_j$
given by Martin and Steel [Reference Martin and Steel13, Theorem 3.12]; the requirement that
$\mathcal {T}_j$
given by Martin and Steel [Reference Martin and Steel13, Theorem 3.12]; the requirement that
![]() $\mathcal {M}_{b_j}^{\pi _j\mathcal {T}_j}$
is wellfounded was only necessary for stage
$\mathcal {M}_{b_j}^{\pi _j\mathcal {T}_j}$
is wellfounded was only necessary for stage
![]() $j=0$
to establish that
$j=0$
to establish that
![]() $(\mathcal {T}_{0}, b_{0})\in W$
.) Furthermore, given a generic enumeration
$(\mathcal {T}_{0}, b_{0})\in W$
.) Furthermore, given a generic enumeration
![]() $\{x_j : j < \omega \}$
of
$\{x_j : j < \omega \}$
of
![]() $\mathbb {R}^V$
in
$\mathbb {R}^V$
in
![]() $V^{\mathrm {Col}(\omega ,\mathbb {R})}$
, we do this in such a way to produce a
$V^{\mathrm {Col}(\omega ,\mathbb {R})}$
, we do this in such a way to produce a
![]() $\pi _0$
-realizable
$\pi _0$
-realizable
![]() $\mathbb {R}$
-genericity iteration
$\mathbb {R}$
-genericity iteration
![]() $P_0 \to P_1 \to \cdots P_\omega $
. With suitable bookkeeping, one can do this in such a way that the Woodin cardinals
$P_0 \to P_1 \to \cdots P_\omega $
. With suitable bookkeeping, one can do this in such a way that the Woodin cardinals
![]() $i_{j,\omega }(\delta _j)$
for
$i_{j,\omega }(\delta _j)$
for
![]() $j<\omega $
are cofinal in
$j<\omega $
are cofinal in
![]() $i_{0,\omega }(\bar {\lambda })$
, and the generic filters
$i_{0,\omega }(\bar {\lambda })$
, and the generic filters
![]() $g_j$
for
$g_j$
for
![]() $j<\omega $
fit together into a
$j<\omega $
fit together into a
![]() $P_\omega $
-generic filter
$P_\omega $
-generic filter
![]() $g \subseteq \mathrm {Col}(\omega ,\mathord {<}i_{0,\omega }(\bar {\lambda }))$
(as in Remark 6.2) such that
$g \subseteq \mathrm {Col}(\omega ,\mathord {<}i_{0,\omega }(\bar {\lambda }))$
(as in Remark 6.2) such that
![]() $\mathbb {R}^V = \bigcup \{\mathbb {R} \cap P_{\omega }[g \mathord {\restriction } \xi ] : \xi < i_{0\omega }(\bar {\lambda })\}$
.
$\mathbb {R}^V = \bigcup \{\mathbb {R} \cap P_{\omega }[g \mathord {\restriction } \xi ] : \xi < i_{0\omega }(\bar {\lambda })\}$
.
To see that (1) implies (2), it remains to observe that the condition
![]() $x \in A$
is equivalent to the condition
$x \in A$
is equivalent to the condition
![]() $P_\omega (\mathbb {R}^V) \models \psi \big [i_{0,\omega }(\bar {S}),x\big ]$
by the hypothesis of the lemma and the fact that
$P_\omega (\mathbb {R}^V) \models \psi \big [i_{0,\omega }(\bar {S}),x\big ]$
by the hypothesis of the lemma and the fact that
![]() $C = \mathrm {p}[i_{0,\omega }(\bar {S})]^{P_\omega (\mathbb {R}^V)}$
, as in Remark 6.4. This in turn is equivalent to the condition that
$C = \mathrm {p}[i_{0,\omega }(\bar {S})]^{P_\omega (\mathbb {R}^V)}$
, as in Remark 6.4. This in turn is equivalent to the condition that
![]() $\psi \big [\mathrm {p}[i_{0,1}(\bar {S})],x\big ]$
holds in the symmetric extension of
$\psi \big [\mathrm {p}[i_{0,1}(\bar {S})],x\big ]$
holds in the symmetric extension of
![]() $P_1[g_0]$
at its limit
$P_1[g_0]$
at its limit
![]() $i_{0,1}(\bar {\lambda })$
of Woodin cardinals (i.e., that the first step of our iteration witnessed (2)) by the fact that the iteration map
$i_{0,1}(\bar {\lambda })$
of Woodin cardinals (i.e., that the first step of our iteration witnessed (2)) by the fact that the iteration map
![]() $i_{1,\omega } : P_1 \to P_\omega $
extends to an elementary embedding
$i_{1,\omega } : P_1 \to P_\omega $
extends to an elementary embedding
![]() $i^*_{1,\omega } : P_1[g_0] \to P_\omega [g_0]$
.
$i^*_{1,\omega } : P_1[g_0] \to P_\omega [g_0]$
.
The proof that (2) implies (1) is the same, except that the first step of the genericity iteration is given by assuming (2), and the two equivalences in the previous paragraph are applied in reverse.
This characterization of the set A given by the equivalence of (1) and (2) shows that A is a projection of a
![]() $\mathord {<}\lambda $
-homogeneously Suslin set (essentially all of whose complexity comes from W) – that is, that A is
$\mathord {<}\lambda $
-homogeneously Suslin set (essentially all of whose complexity comes from W) – that is, that A is
![]() $\mathord {<}\lambda $
-weakly homogeneously Suslin. It follows that
$\mathord {<}\lambda $
-weakly homogeneously Suslin. It follows that
![]() $\lambda $
is
$\lambda $
is
![]() $\mathord {<}\lambda $
-homogeneously Suslin by the main theorem from the proof of projective determinacy (Martin and Steel [Reference Martin and Steel12, Theorem 5.11]; see also Theorem 3.3.13 of [Reference Larson10]).
$\mathord {<}\lambda $
-homogeneously Suslin by the main theorem from the proof of projective determinacy (Martin and Steel [Reference Martin and Steel12, Theorem 5.11]; see also Theorem 3.3.13 of [Reference Larson10]).
7 Absoluteness of the F predicate
Although our main theorem is concerned only with the predicate F as it is defined in the symmetric model
![]() $V(\mathbb {R}^*_G)$
, the proof of
$V(\mathbb {R}^*_G)$
, the proof of
![]() $\Sigma ^2_1$
reflection will need to consider the predicate as it is defined in other models (in particular V and
$\Sigma ^2_1$
reflection will need to consider the predicate as it is defined in other models (in particular V and
![]() $\mathbb {R}$
-genericity iterates of countable hulls of rank initial segments of V) and show that the definition satisfies a certain absoluteness property between these models (as in Lemma 7.5 below).
$\mathbb {R}$
-genericity iterates of countable hulls of rank initial segments of V) and show that the definition satisfies a certain absoluteness property between these models (as in Lemma 7.5 below).
First, we will need a lemma that shows that, in the presence of Woodin cardinals, the universally Baire sets added generically over a countable model that embeds into V are closely related to universally Baire sets in V.
In the presence of Woodin cardinals, the pointclass of (sufficiently) homogeneously Suslin sets is closed under complementation in a strong sense. That is, if
![]() $\delta $
is a Woodin cardinal, Y is a set of
$\delta $
is a Woodin cardinal, Y is a set of
![]() $\delta ^+$
-complete measures with
$\delta ^+$
-complete measures with
![]() $|Y| < \delta $
, and
$|Y| < \delta $
, and
![]() $\kappa < \delta $
is a cardinal, then by Steel [Reference Steel, Gao, Jackson and Zhang22, Lemma 2.1], there is a ‘tower-flipping’ function f that associates to every finite tower
$\kappa < \delta $
is a cardinal, then by Steel [Reference Steel, Gao, Jackson and Zhang22, Lemma 2.1], there is a ‘tower-flipping’ function f that associates to every finite tower
![]() $\langle \rho _0,\ldots ,\rho _{n-1}\rangle $
of measures from Y a length-n tower
$\langle \rho _0,\ldots ,\rho _{n-1}\rangle $
of measures from Y a length-n tower
![]() $f(\langle \rho _0,\ldots ,\rho _{n-1}\rangle )$
of
$f(\langle \rho _0,\ldots ,\rho _{n-1}\rangle )$
of
![]() $\kappa $
-complete measures with the following properties. First, f respects extensions of finite towers, so that to every infinite tower
$\kappa $
-complete measures with the following properties. First, f respects extensions of finite towers, so that to every infinite tower
![]() $\vec {\rho }$
of measures from Y, it continuously associates an infinite tower
$\vec {\rho }$
of measures from Y, it continuously associates an infinite tower
![]() $\bigcup _{n<\omega } f(\vec {\rho } \mathord {\restriction } n)$
of
$\bigcup _{n<\omega } f(\vec {\rho } \mathord {\restriction } n)$
of
![]() $\kappa $
-complete measures. Second, this associated tower
$\kappa $
-complete measures. Second, this associated tower
![]() $\bigcup _{n<\omega } f(\vec {\rho } \mathord {\restriction } n)$
is wellfounded if and only if the given tower
$\bigcup _{n<\omega } f(\vec {\rho } \mathord {\restriction } n)$
is wellfounded if and only if the given tower
![]() $\vec {\rho }$
is ill-founded. Third, this property of the tower-flipping function continues to hold in all generic extensions by posets of size less than
$\vec {\rho }$
is ill-founded. Third, this property of the tower-flipping function continues to hold in all generic extensions by posets of size less than
![]() $\kappa $
.
$\kappa $
.
The following lemma shows that in the presence of a Woodin cardinal, the Martin–Solovay construction can be used to produce absolutely complementing trees of a nice form, which we will use in Lemma 7.3 to prove an absoluteness result for the F predicate. A similar idea appears in the proof of Steel [Reference Steel, Gao, Jackson and Zhang22, Theorem 2.2, Subclaim 1.1].
For a tree T and a natural number n, we let
![]() $T \mathord {\mathord {\restriction }} n$
be the subset of T consisting of all nodes of length less than n.
$T \mathord {\mathord {\restriction }} n$
be the subset of T consisting of all nodes of length less than n.
Lemma 7.1. Let P be a countable transitive set, let
![]() $\gamma $
be a limit ordinal, and let
$\gamma $
be a limit ordinal, and let
![]() $\pi \colon P \to V_{\gamma }$
be an elementary embedding. Let
$\pi \colon P \to V_{\gamma }$
be an elementary embedding. Let
![]() $\bar {\alpha }$
be a cardinal of P, and suppose that
$\bar {\alpha }$
be a cardinal of P, and suppose that
![]() $\bar {\delta }$
is a Woodin cardinal of P with
$\bar {\delta }$
is a Woodin cardinal of P with
![]() $\bar {\alpha } < \bar {\delta }$
. Let
$\bar {\alpha } < \bar {\delta }$
. Let
![]() $g \subseteq \mathrm {Col}(\omega ,\bar {\alpha })$
be a P-generic filter in V, and let A be a
$g \subseteq \mathrm {Col}(\omega ,\bar {\alpha })$
be a P-generic filter in V, and let A be a
![]() $\bar {\delta }^+$
-homogeneously Suslin set of reals in
$\bar {\delta }^+$
-homogeneously Suslin set of reals in
![]() $P[g]$
.
$P[g]$
.
Then for each cardinal
![]() $\bar {\kappa }$
of P with
$\bar {\kappa }$
of P with
![]() $\bar {\alpha } < \bar {\kappa } < \bar {\delta }$
, there is a
$\bar {\alpha } < \bar {\kappa } < \bar {\delta }$
, there is a
![]() $\bar {\kappa }$
-absolutely complementing pair of trees
$\bar {\kappa }$
-absolutely complementing pair of trees
![]() $(\bar {S},\bar {T}) \in P[g]$
for A such that, for every
$(\bar {S},\bar {T}) \in P[g]$
for A such that, for every
![]() $n < \omega $
, the restrictions
$n < \omega $
, the restrictions
![]() $\bar {S}\mathord {\restriction } n$
and
$\bar {S}\mathord {\restriction } n$
and
![]() $\bar {T} \mathord {\restriction } n$
to finite levels are in P, and, letting
$\bar {T} \mathord {\restriction } n$
to finite levels are in P, and, letting
![]() $S = \bigcup _{n<\omega } \pi (\bar {S}\mathord {\restriction } n)$
and
$S = \bigcup _{n<\omega } \pi (\bar {S}\mathord {\restriction } n)$
and
![]() $T = \bigcup _{n<\omega } \pi (\bar {T}\mathord {\restriction } n)$
, the pair
$T = \bigcup _{n<\omega } \pi (\bar {T}\mathord {\restriction } n)$
, the pair
![]() $(S,T) \in V_{\gamma }$
is
$(S,T) \in V_{\gamma }$
is
![]() $\pi (\bar {\kappa })$
-absolutely complementing.
$\pi (\bar {\kappa })$
-absolutely complementing.
Proof. Let
![]() $A = \textbf {S}_{\vec {\mu }}$
where
$A = \textbf {S}_{\vec {\mu }}$
where
![]() $\vec {\mu }$
is a tree of
$\vec {\mu }$
is a tree of
![]() $\bar {\delta }^+$
-complete measures in
$\bar {\delta }^+$
-complete measures in
![]() $P[g]$
. By the Levy–Solovay theorem, each measure
$P[g]$
. By the Levy–Solovay theorem, each measure
![]() $\mu _s$
is induced by the
$\mu _s$
is induced by the
![]() $\bar {\delta }^+$
-complete measure
$\bar {\delta }^+$
-complete measure
![]() $\mu _s \cap P \in P$
, which we will also denote by
$\mu _s \cap P \in P$
, which we will also denote by
![]() $\mu _s$
. In P, there is a set Y consisting of
$\mu _s$
. In P, there is a set Y consisting of
![]() $\bar {\delta }^+$
-complete measures such that
$\bar {\delta }^+$
-complete measures such that
![]() $|Y|^{P} = \bar {\alpha }$
every member of
$|Y|^{P} = \bar {\alpha }$
every member of
![]() $\vec {\mu }$
is induced by a member of Y.
$\vec {\mu }$
is induced by a member of Y.
Given a cardinal
![]() $\bar {\kappa }$
of P with
$\bar {\kappa }$
of P with
![]() $\bar {\alpha } < \bar {\kappa } < \bar {\delta }$
(as in the statement of the lemma), let
$\bar {\alpha } < \bar {\kappa } < \bar {\delta }$
(as in the statement of the lemma), let
![]() $f \in P$
be a tower-flipping function that continuously associates to every tower of measures from Y a tower of
$f \in P$
be a tower-flipping function that continuously associates to every tower of measures from Y a tower of
![]() $\bar {\kappa }$
-complete measures. In
$\bar {\kappa }$
-complete measures. In
![]() $P[g]$
, define the tree of
$P[g]$
, define the tree of
![]() $\bar {\kappa }$
-complete measures
$\bar {\kappa }$
-complete measures
![]() $\vec {\nu } = \langle \nu _s : s \in \omega ^{\mathord {<}\omega }\rangle $
that is continuously associated to
$\vec {\nu } = \langle \nu _s : s \in \omega ^{\mathord {<}\omega }\rangle $
that is continuously associated to
![]() $\vec {\mu }$
by f in the sense that
$\vec {\mu }$
by f in the sense that
![]() $\langle \nu _{s \mathord {\restriction } n} : n \le \left |s\right |\rangle = f(\langle \mu _{s \mathord {\restriction } n} :n \le \left |s\right |\rangle )$
for every finite sequence
$\langle \nu _{s \mathord {\restriction } n} : n \le \left |s\right |\rangle = f(\langle \mu _{s \mathord {\restriction } n} :n \le \left |s\right |\rangle )$
for every finite sequence
![]() $s \in \omega ^{\mathord {<}\omega }$
. So in
$s \in \omega ^{\mathord {<}\omega }$
. So in
![]() $P[g]$
, we have
$P[g]$
, we have
![]() $\textbf {S}_{\vec {\nu }} = \omega ^\omega \setminus \textbf {S}_{\vec {\mu }}$
by the tower-flipping property of f. Moreover,
$\textbf {S}_{\vec {\nu }} = \omega ^\omega \setminus \textbf {S}_{\vec {\mu }}$
by the tower-flipping property of f. Moreover,
![]() $\pi (f)$
is a tower-flipping function in
$\pi (f)$
is a tower-flipping function in
![]() $V_{\gamma }$
by the elementarity of
$V_{\gamma }$
by the elementarity of
![]() $\pi $
, so we have
$\pi $
, so we have
![]() $\textbf {S}_{\pi "\vec {\nu }} = \omega ^\omega \setminus \textbf {S}_{\pi "\vec {\mu }}$
in
$\textbf {S}_{\pi "\vec {\nu }} = \omega ^\omega \setminus \textbf {S}_{\pi "\vec {\mu }}$
in
![]() $V_{\gamma }$
.
$V_{\gamma }$
.
In
![]() $P[g]$
, define the Martin–Solovay trees
$P[g]$
, define the Martin–Solovay trees
![]() $\bar {S} = \operatorname {\mathrm {ms}}(\vec {\mu })$
and
$\bar {S} = \operatorname {\mathrm {ms}}(\vec {\mu })$
and
![]() $\bar {T} = \operatorname {\mathrm {ms}}(\vec {\nu })$
, and in
$\bar {T} = \operatorname {\mathrm {ms}}(\vec {\nu })$
, and in
![]() $V_{\gamma }$
, define the Martin–Solovay trees
$V_{\gamma }$
, define the Martin–Solovay trees
![]() $S = \operatorname {\mathrm {ms}}(\pi "\vec {\mu })$
and
$S = \operatorname {\mathrm {ms}}(\pi "\vec {\mu })$
and
![]() $T = \operatorname {\mathrm {ms}}(\pi "\vec {\nu })$
. Because for each
$T = \operatorname {\mathrm {ms}}(\pi "\vec {\nu })$
. Because for each
![]() $n \in \omega $
the first n levels of the Martin–Solovay tree are determined by finitely many measures (in the ground model, by the absoluteness of the construction of the Martin-Solovay tree between P and
$n \in \omega $
the first n levels of the Martin–Solovay tree are determined by finitely many measures (in the ground model, by the absoluteness of the construction of the Martin-Solovay tree between P and
![]() $P[g]$
for
$P[g]$
for
![]() $\bar {\delta }^{+}$
-complete measures), we have
$\bar {\delta }^{+}$
-complete measures), we have
![]() $(\bar {S} \mathord {\restriction } n,\bar {T} \mathord {\restriction } n) \in P$
for all
$(\bar {S} \mathord {\restriction } n,\bar {T} \mathord {\restriction } n) \in P$
for all
![]() $n<\omega $
. For the same reason, we have
$n<\omega $
. For the same reason, we have
![]() $S = \bigcup _{n<\omega } \pi (\bar {S}\mathord {\restriction } n)$
and
$S = \bigcup _{n<\omega } \pi (\bar {S}\mathord {\restriction } n)$
and
![]() $T = \bigcup _{n<\omega } \pi (\bar {T}\mathord {\restriction } n)$
.
$T = \bigcup _{n<\omega } \pi (\bar {T}\mathord {\restriction } n)$
.
In the model
![]() $P[g]$
, the pair
$P[g]$
, the pair
![]() $(\bar {S},\bar {T})$
is
$(\bar {S},\bar {T})$
is
![]() $\bar {\kappa }$
-absolutely complementing: this follows from the fact that
$\bar {\kappa }$
-absolutely complementing: this follows from the fact that
![]() $\mathrm {p}[\bar {S}] = \omega ^\omega \setminus \mathrm {p}[\bar {T}]$
(in
$\mathrm {p}[\bar {S}] = \omega ^\omega \setminus \mathrm {p}[\bar {T}]$
(in
![]() $P[g]$
) and the fact that
$P[g]$
) and the fact that
![]() $\bar {S}$
and
$\bar {S}$
and
![]() $\bar {T}$
, being Martin–Solovay trees, are each
$\bar {T}$
, being Martin–Solovay trees, are each
![]() $\bar {\kappa }$
-absolutely complemented. A similar argument shows that in V, the pair
$\bar {\kappa }$
-absolutely complemented. A similar argument shows that in V, the pair
![]() $(S,T)$
is
$(S,T)$
is
![]() $\pi (\bar {\kappa })$
-absolutely complementing, as desired.
$\pi (\bar {\kappa })$
-absolutely complementing, as desired.
Using a strong cardinal, we can strengthen the previous lemma to give any desired degree of absolute complementation.
Lemma 7.2. Let P be a countable transitive set, let
![]() $\gamma $
be a limit ordinal, and let
$\gamma $
be a limit ordinal, and let
![]() $\pi \colon P \to V_{\gamma }$
be an elementary embedding. Let
$\pi \colon P \to V_{\gamma }$
be an elementary embedding. Let
![]() $\bar {\alpha }$
be a cardinal of P, and let
$\bar {\alpha }$
be a cardinal of P, and let
![]() $\bar {\delta }$
be a Woodin cardinal of P with
$\bar {\delta }$
be a Woodin cardinal of P with
![]() $\bar {\alpha } < \bar {\delta }$
. Let
$\bar {\alpha } < \bar {\delta }$
. Let
![]() $g \subseteq \mathrm {Col}(\omega ,\bar {\alpha })$
be a P-generic filter in V, and let A be a
$g \subseteq \mathrm {Col}(\omega ,\bar {\alpha })$
be a P-generic filter in V, and let A be a
![]() $\bar {\delta }^+$
-homogeneously Suslin set of reals in
$\bar {\delta }^+$
-homogeneously Suslin set of reals in
![]() $P[g]$
.
$P[g]$
.
Let
![]() $\bar {\kappa }$
and
$\bar {\kappa }$
and
![]() $\bar {\eta }$
be cardinals of P with
$\bar {\eta }$
be cardinals of P with
![]() $\bar {\alpha } < \bar {\kappa } < \bar {\delta } < \bar {\eta }$
such that
$\bar {\alpha } < \bar {\kappa } < \bar {\delta } < \bar {\eta }$
such that
![]() $\bar {\kappa }$
is
$\bar {\kappa }$
is
![]() $(\bar {\eta }+1)$
-strong in P. Then there is an
$(\bar {\eta }+1)$
-strong in P. Then there is an
![]() $\bar {\eta }$
-absolutely complementing pair of trees
$\bar {\eta }$
-absolutely complementing pair of trees
![]() $(\bar {S},\bar {T}) \in P[g]$
for A such that for every
$(\bar {S},\bar {T}) \in P[g]$
for A such that for every
![]() $n < \omega $
, the restrictions
$n < \omega $
, the restrictions
![]() $\bar {S}\mathord {\restriction } n$
and
$\bar {S}\mathord {\restriction } n$
and
![]() $\bar {T} \mathord {\restriction } n$
to finite levels are in P, and letting
$\bar {T} \mathord {\restriction } n$
to finite levels are in P, and letting
![]() $S = \bigcup _{n<\omega } \pi (\bar {S}\mathord {\restriction } n)$
and
$S = \bigcup _{n<\omega } \pi (\bar {S}\mathord {\restriction } n)$
and
![]() $T = \bigcup _{n<\omega } \pi (\bar {T}\mathord {\restriction } n)$
, the pair
$T = \bigcup _{n<\omega } \pi (\bar {T}\mathord {\restriction } n)$
, the pair
![]() $(S,T) \in V_{\gamma }$
is
$(S,T) \in V_{\gamma }$
is
![]() $\pi (\bar {\eta })$
-absolutely complementing.
$\pi (\bar {\eta })$
-absolutely complementing.
Proof. Let
![]() $(\kappa , \eta ) = \pi (\bar {\kappa }, \bar {\eta })$
. By Lemma 7.1, there is a
$(\kappa , \eta ) = \pi (\bar {\kappa }, \bar {\eta })$
. By Lemma 7.1, there is a
![]() $\bar {\kappa }$
-absolutely complementing pair of trees
$\bar {\kappa }$
-absolutely complementing pair of trees
![]() $(\bar {S}_0, \bar {T}_0)$
in
$(\bar {S}_0, \bar {T}_0)$
in
![]() $P[g]$
for A such that for every
$P[g]$
for A such that for every
![]() $n < \omega $
, the restrictions
$n < \omega $
, the restrictions
![]() $\bar {S}_0\mathord {\restriction } n$
and
$\bar {S}_0\mathord {\restriction } n$
and
![]() $\bar {T}_0 \mathord {\restriction } n$
to finite levels are in P, and letting
$\bar {T}_0 \mathord {\restriction } n$
to finite levels are in P, and letting
![]() $S_0 = \bigcup _{n<\omega } \pi (\bar {S}_0\mathord {\restriction } n)$
and
$S_0 = \bigcup _{n<\omega } \pi (\bar {S}_0\mathord {\restriction } n)$
and
![]() $T_0 = \bigcup _{n<\omega } \pi (\bar {T}_0\mathord {\restriction } n)$
, the pair
$T_0 = \bigcup _{n<\omega } \pi (\bar {T}_0\mathord {\restriction } n)$
, the pair
![]() $(S_0,T_0) \in V_{\gamma }$
is
$(S_0,T_0) \in V_{\gamma }$
is
![]() $\kappa $
-absolutely complementing.
$\kappa $
-absolutely complementing.
In P, let
![]() $\bar {E}$
be an extender witnessing that
$\bar {E}$
be an extender witnessing that
![]() $\bar {\kappa }$
is
$\bar {\kappa }$
is
![]() $(\bar {\eta }+1)$
-strong. The ultrapower map
$(\bar {\eta }+1)$
-strong. The ultrapower map
![]() $j_{\bar {E}} \colon P \to \operatorname {\mathrm {Ult}}(P, \bar {E})$
extends canonically to a map
$j_{\bar {E}} \colon P \to \operatorname {\mathrm {Ult}}(P, \bar {E})$
extends canonically to a map
![]() $P[g] \to \operatorname {\mathrm {Ult}}(P[g], \bar {E})$
, which we will also denote by
$P[g] \to \operatorname {\mathrm {Ult}}(P[g], \bar {E})$
, which we will also denote by
![]() $j_{\bar {E}}$
. In
$j_{\bar {E}}$
. In
![]() $V_{\gamma }$
, the extender
$V_{\gamma }$
, the extender
![]() $E = \pi (\bar {E})$
witnesses that
$E = \pi (\bar {E})$
witnesses that
![]() $\kappa $
is
$\kappa $
is
![]() $(\eta +1)$
-strong, and we have an ultrapower map
$(\eta +1)$
-strong, and we have an ultrapower map
![]() $j_E : V_{\gamma } \to \operatorname {\mathrm {Ult}}(V_{\gamma }, E)$
with
$j_E : V_{\gamma } \to \operatorname {\mathrm {Ult}}(V_{\gamma }, E)$
with
![]() $j_{E}(\kappa )> \eta $
and
$j_{E}(\kappa )> \eta $
and
![]() $V_{\eta + 1} \subseteq \operatorname {\mathrm {Ult}}(V_{\gamma }, E)$
.
$V_{\eta + 1} \subseteq \operatorname {\mathrm {Ult}}(V_{\gamma }, E)$
.
Letting
![]() $\bar {S} = j_{\bar {E}}(\bar {S}_0)$
and
$\bar {S} = j_{\bar {E}}(\bar {S}_0)$
and
![]() $\bar {T} = j_{\bar {E}}(\bar {T}_0)$
, the pair of trees
$\bar {T} = j_{\bar {E}}(\bar {T}_0)$
, the pair of trees
![]() $(\bar {S}, \bar {T})$
is an
$(\bar {S}, \bar {T})$
is an
![]() $\bar {\eta }$
-absolutely complementing pair for A in
$\bar {\eta }$
-absolutely complementing pair for A in
![]() $P[g]$
. Similarly, letting
$P[g]$
. Similarly, letting
![]() $S = j_E(S_0)$
and
$S = j_E(S_0)$
and
![]() $T = j_E(T_0)$
, the pair of trees
$T = j_E(T_0)$
, the pair of trees
![]() $(S, T) \in V_{\gamma }$
is
$(S, T) \in V_{\gamma }$
is
![]() $\eta $
-absolutely complementing. Because
$\eta $
-absolutely complementing. Because
![]() $\pi \circ j_{\bar {E}} = j_E \circ \pi $
, we have
$\pi \circ j_{\bar {E}} = j_E \circ \pi $
, we have
![]() $S = \bigcup _{n<\omega } \pi (\bar {S}\mathord {\restriction } n)$
and
$S = \bigcup _{n<\omega } \pi (\bar {S}\mathord {\restriction } n)$
and
![]() $T = \bigcup _{n<\omega } \pi (\bar {T}\mathord {\restriction } n)$
, as desired.
$T = \bigcup _{n<\omega } \pi (\bar {T}\mathord {\restriction } n)$
, as desired.
Applying Lemma 7.2 to
![]() $\mathbb {R}$
-genericity iterations yields the following result. Part (1) below can also be derived as an immediate consequence of Steel [Reference Steel, Gao, Jackson and Zhang22, Subclaim 1.1], which applies more generally to any limit
$\mathbb {R}$
-genericity iterations yields the following result. Part (1) below can also be derived as an immediate consequence of Steel [Reference Steel, Gao, Jackson and Zhang22, Subclaim 1.1], which applies more generally to any limit
![]() $\lambda $
of Woodin cardinals. However, in our situation, we can use the fact that
$\lambda $
of Woodin cardinals. However, in our situation, we can use the fact that
![]() $\lambda $
is also a limit of strong cardinals to give a proof of part (1) using Lemma 7.2 instead. Part (2
$\lambda $
is also a limit of strong cardinals to give a proof of part (1) using Lemma 7.2 instead. Part (2
Lemma 7.3. Let
![]() $\lambda $
be a limit of Woodin cardinals and a limit of strong cardinals, and let
$\lambda $
be a limit of Woodin cardinals and a limit of strong cardinals, and let
![]() $\gamma $
be a limit ordinal of cofinality greater than
$\gamma $
be a limit ordinal of cofinality greater than
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $P_{0}$
be a countable transitive set, and let
$P_{0}$
be a countable transitive set, and let
![]() $\pi _0 \colon P_0 \to V_{\gamma }$
be an elementary embedding with
$\pi _0 \colon P_0 \to V_{\gamma }$
be an elementary embedding with
![]() $\lambda \in \operatorname {\mathrm {ran}}(\pi _0)$
. Let
$\lambda \in \operatorname {\mathrm {ran}}(\pi _0)$
. Let
![]() $P_\omega $
be obtained from
$P_\omega $
be obtained from
![]() $P_0$
by a
$P_0$
by a
![]() $\pi _0$
-realizable
$\pi _0$
-realizable
![]() $\mathbb {R}$
-genericity iteration at
$\mathbb {R}$
-genericity iteration at
![]() $\lambda $
, and let A be a set of reals in
$\lambda $
, and let A be a set of reals in
![]() $\mathrm {uB}^{P_\omega (\mathbb {R}^V)}$
. Then the following hold.
$\mathrm {uB}^{P_\omega (\mathbb {R}^V)}$
. Then the following hold.
-
1.
 $A \in \mathrm {uB}^V$
$A \in \mathrm {uB}^V$
-
2. For every set
 $Z \in P_\omega (\mathbb {R}^V) \cap V$
, every condition
$Z \in P_\omega (\mathbb {R}^V) \cap V$
, every condition
 $p \in \mathrm {Col}(\omega ,Z)$
, and every
$p \in \mathrm {Col}(\omega ,Z)$
, and every
 $\mathrm {Col}(\omega ,Z)$
-name
$\mathrm {Col}(\omega ,Z)$
-name
 $\dot {x} \in P_\omega (\mathbb {R}^V) \cap V$
for a real, the statement ‘p forces
$\dot {x} \in P_\omega (\mathbb {R}^V) \cap V$
for a real, the statement ‘p forces
 $\dot {x}$
to be in the canonical expansion of A’ is absolute between
$\dot {x}$
to be in the canonical expansion of A’ is absolute between
 $P_\omega (\mathbb {R}^V)$
and V.
$P_\omega (\mathbb {R}^V)$
and V.
Proof. In terms of the notation for
![]() $\mathbb {R}$
-genericity iterations given in (and just after) Definition 6.1, the set
$\mathbb {R}$
-genericity iterations given in (and just after) Definition 6.1, the set
![]() $A \in \mathrm {uB}^{P_\omega (\mathbb {R}^V)}$
is represented by a pair of absolutely
$A \in \mathrm {uB}^{P_\omega (\mathbb {R}^V)}$
is represented by a pair of absolutely
![]() $\pi ^{-1}_{\omega }(\lambda )$
-complementing trees in
$\pi ^{-1}_{\omega }(\lambda )$
-complementing trees in
![]() $P_{\omega }(\mathbb {R}^{V})$
, which, by the usual homogeneity argument, exist in
$P_{\omega }(\mathbb {R}^{V})$
, which, by the usual homogeneity argument, exist in
![]() $P_{\omega }[g_{j_{0}}]$
, for some
$P_{\omega }[g_{j_{0}}]$
, for some
![]() $j_{0} < \omega $
. Since
$j_{0} < \omega $
. Since
![]() $P_{\omega }$
is the direct limit of
$P_{\omega }$
is the direct limit of
![]() $\langle P_{i} : i < \omega \rangle $
, these trees can be taken to be in the range of
$\langle P_{i} : i < \omega \rangle $
, these trees can be taken to be in the range of
![]() $i^{*}_{j,\omega }$
(the canonical extension of
$i^{*}_{j,\omega }$
(the canonical extension of
![]() $i_{j,\omega }$
to
$i_{j,\omega }$
to
![]() $P_{j}[g_{j-1}]$
) for some positive
$P_{j}[g_{j-1}]$
) for some positive
![]() $j < \omega $
. Otherwise stated, A comes from a set
$j < \omega $
. Otherwise stated, A comes from a set
![]() $A_j \in \mathrm {uB}^{P_j[g_{j-1}]}$
appearing at stage j, in the sense that
$A_j \in \mathrm {uB}^{P_j[g_{j-1}]}$
appearing at stage j, in the sense that
![]() $A = i_{j,\omega }^*(A_j)^{P_\omega (\mathbb {R}^V)}$
.
$A = i_{j,\omega }^*(A_j)^{P_\omega (\mathbb {R}^V)}$
.
To prove part (1), we apply Lemma 7.2 with
![]() $P = P_j,\ \gamma = \gamma , \ \pi = \pi _j, \ g = g_{j-1}, \ A = A_j, \ \bar {\alpha } = i_{j-1,j}(\delta _{j-1}), \ \bar {\kappa }$
equal to the least strong cardinal of
$P = P_j,\ \gamma = \gamma , \ \pi = \pi _j, \ g = g_{j-1}, \ A = A_j, \ \bar {\alpha } = i_{j-1,j}(\delta _{j-1}), \ \bar {\kappa }$
equal to the least strong cardinal of
![]() $P_j$
above
$P_j$
above
![]() $i_{j-1,j}(\delta _{j-1}), \ \bar {\delta }$
equal to the least Woodin cardinal of
$i_{j-1,j}(\delta _{j-1}), \ \bar {\delta }$
equal to the least Woodin cardinal of
![]() $P_j$
above
$P_j$
above
![]() $\bar {\kappa }$
, and
$\bar {\kappa }$
, and
![]() $\bar {\eta } = \pi _j^{-1}(\lambda )$
. This gives us a pair of
$\bar {\eta } = \pi _j^{-1}(\lambda )$
. This gives us a pair of
![]() $\pi ^{-1}_j(\lambda )$
-absolutely complementing trees
$\pi ^{-1}_j(\lambda )$
-absolutely complementing trees
![]() $(\bar {S},\bar {T}) \in P_j[g_{j-1}]$
for
$(\bar {S},\bar {T}) \in P_j[g_{j-1}]$
for
![]() $A_j$
such that for every
$A_j$
such that for every
![]() $n < \omega $
, the restrictions
$n < \omega $
, the restrictions
![]() $\bar {S}\mathord {\restriction } n$
and
$\bar {S}\mathord {\restriction } n$
and
![]() $\bar {T} \mathord {\restriction } n$
to finite levels are in
$\bar {T} \mathord {\restriction } n$
to finite levels are in
![]() $P_j$
, and letting
$P_j$
, and letting
![]() $S = \bigcup _{n<\omega } \pi _j(\bar {S}\mathord {\restriction } n)$
and
$S = \bigcup _{n<\omega } \pi _j(\bar {S}\mathord {\restriction } n)$
and
![]() $T = \bigcup _{n<\omega } \pi _j(\bar {T}\mathord {\restriction } n)$
, the pair
$T = \bigcup _{n<\omega } \pi _j(\bar {T}\mathord {\restriction } n)$
, the pair
![]() $(S,T)$
is
$(S,T)$
is
![]() $\lambda $
-absolutely complementing in V.
$\lambda $
-absolutely complementing in V.
Since
![]() $\pi _{\omega } \circ i_{j,\omega } = \pi _{j}, \ \pi _{\omega }(i_{j,\omega }(\bar {S} \mathord {\restriction } n)) = \pi _{j}(\bar {S} \mathord {\restriction } n)$
and
$\pi _{\omega } \circ i_{j,\omega } = \pi _{j}, \ \pi _{\omega }(i_{j,\omega }(\bar {S} \mathord {\restriction } n)) = \pi _{j}(\bar {S} \mathord {\restriction } n)$
and
![]() $\pi _{\omega }(i_{j,\omega }(\bar {T} \mathord {\restriction } n)) = \pi _{j}(\bar {T} \mathord {\restriction } n)$
for each
$\pi _{\omega }(i_{j,\omega }(\bar {T} \mathord {\restriction } n)) = \pi _{j}(\bar {T} \mathord {\restriction } n)$
for each
![]() $n \in \omega $
, so
$n \in \omega $
, so
![]() $S = \pi _{\omega }(i^{*}_{j,\omega }(\bar {S}))$
and
$S = \pi _{\omega }(i^{*}_{j,\omega }(\bar {S}))$
and
![]() $T = \pi _{\omega }(i^{*}_{j,\omega }(\bar {T}))$
. This implies that
$T = \pi _{\omega }(i^{*}_{j,\omega }(\bar {T}))$
. This implies that
![]() $\pi _\omega " (i_{j,\omega }^*(\bar {S})) \subseteq S$
and
$\pi _\omega " (i_{j,\omega }^*(\bar {S})) \subseteq S$
and
![]() $\pi _\omega " (i_{j,\omega }^*(\bar {T})) \subseteq T$
. It follows that the realization map
$\pi _\omega " (i_{j,\omega }^*(\bar {T})) \subseteq T$
. It follows that the realization map
![]() $\pi _\omega $
takes branches of
$\pi _\omega $
takes branches of
![]() $i_{j,\omega }^*(\bar {S})$
and
$i_{j,\omega }^*(\bar {S})$
and
![]() $i_{j,\omega }^*(\bar {T})$
pointwise to branches of S and T, respectively, so the projections of these trees satisfy the inclusions
$i_{j,\omega }^*(\bar {T})$
pointwise to branches of S and T, respectively, so the projections of these trees satisfy the inclusions
![]() $\mathrm {p}[i_{j,\omega }^*(\bar {S})] \subseteq \mathrm {p}[S]$
and
$\mathrm {p}[i_{j,\omega }^*(\bar {S})] \subseteq \mathrm {p}[S]$
and
![]() $\mathrm {p}[i_{j,\omega }^*(\bar {T})] \subseteq \mathrm {p}[T]$
.
$\mathrm {p}[i_{j,\omega }^*(\bar {T})] \subseteq \mathrm {p}[T]$
.
Because
![]() $A = \mathrm {p}[i_{j,\omega }^*(\bar {S})] = \omega ^\omega \setminus \mathrm {p}[i_{j,\omega }^*(\bar {T})]$
in
$A = \mathrm {p}[i_{j,\omega }^*(\bar {S})] = \omega ^\omega \setminus \mathrm {p}[i_{j,\omega }^*(\bar {T})]$
in
![]() $P_\omega (\mathbb {R}^V)$
, these two inclusions imply that
$P_\omega (\mathbb {R}^V)$
, these two inclusions imply that
![]() $A = \mathrm {p}[S] = \omega ^\omega \setminus \mathrm {p}[T]$
in V. Therefore, A is in
$A = \mathrm {p}[S] = \omega ^\omega \setminus \mathrm {p}[T]$
in V. Therefore, A is in
![]() $\mathrm {uB}_\lambda ^V$
, which is equal to
$\mathrm {uB}_\lambda ^V$
, which is equal to
![]() $\mathrm {uB}^V$
because there is a strong cardinal less than
$\mathrm {uB}^V$
because there is a strong cardinal less than
![]() $\lambda $
.
$\lambda $
.
For part (2), note that our genericity iteration was formed in some generic extension of
![]() $V_{\gamma }$
by the poset
$V_{\gamma }$
by the poset
![]() $\mathrm {Col}(\omega ,\mathbb {R})$
, and the resulting model
$\mathrm {Col}(\omega ,\mathbb {R})$
, and the resulting model
![]() $P_\omega (\mathbb {R}^V)$
is countable there. In particular, the set Z is countable there. So in a generic extension of
$P_\omega (\mathbb {R}^V)$
is countable there. In particular, the set Z is countable there. So in a generic extension of
![]() $V_{\gamma }$
by the poset
$V_{\gamma }$
by the poset
![]() $\mathrm {Col}(\omega ,\mathbb {R}) \times \mathrm {Col}(\omega ,\omega )$
, which is forcing-equivalent to
$\mathrm {Col}(\omega ,\mathbb {R}) \times \mathrm {Col}(\omega ,\omega )$
, which is forcing-equivalent to
![]() $\mathrm {Col}(\omega ,\mathbb {R})$
, we can find a filter
$\mathrm {Col}(\omega ,\mathbb {R})$
, we can find a filter
![]() $H \subseteq \mathrm {Col}(\omega ,Z)$
that contains the condition p and is both V-generic and
$H \subseteq \mathrm {Col}(\omega ,Z)$
that contains the condition p and is both V-generic and
![]() $P_\omega (\mathbb {R}^V)$
-generic. Let
$P_\omega (\mathbb {R}^V)$
-generic. Let
![]() $x = \dot {x}_H$
. We want to see that the two ways of expanding the set A, given by
$x = \dot {x}_H$
. We want to see that the two ways of expanding the set A, given by
![]() $A \in \mathrm {uB}^{P_\omega (\mathbb {R}^V)}$
and
$A \in \mathrm {uB}^{P_\omega (\mathbb {R}^V)}$
and
![]() $A \in \mathrm {uB}^V$
, respectively, agree on whether x is a member. This would follow from Lemma 2.5 if
$A \in \mathrm {uB}^V$
, respectively, agree on whether x is a member. This would follow from Lemma 2.5 if
![]() $P_\omega (\mathbb {R}^V) \in V$
, but it seems that the condition
$P_\omega (\mathbb {R}^V) \in V$
, but it seems that the condition
![]() $P_\omega (\mathbb {R}^V) \in V$
may fail in general, which is why we seem to need Lemma 7.2.
$P_\omega (\mathbb {R}^V) \in V$
may fail in general, which is why we seem to need Lemma 7.2.
By Lemma 5.7, in the model
![]() $P_\omega (\mathbb {R}^V)$
, there is an ordinal
$P_\omega (\mathbb {R}^V)$
, there is an ordinal
![]() $\eta _\omega \ge \pi _\omega ^{-1}(\lambda )$
such that every
$\eta _\omega \ge \pi _\omega ^{-1}(\lambda )$
such that every
![]() $\eta _\omega $
-absolutely complementing set of trees is Z-absolutely complementing. Increasing j (from the first paragraph of the proof of the lemma) if necessary, we may assume that
$\eta _\omega $
-absolutely complementing set of trees is Z-absolutely complementing. Increasing j (from the first paragraph of the proof of the lemma) if necessary, we may assume that
![]() $\eta _\omega = i_{j,\omega }(\bar {\eta })$
for some ordinal
$\eta _\omega = i_{j,\omega }(\bar {\eta })$
for some ordinal
![]() $\bar {\eta } \in P_j$
.
$\bar {\eta } \in P_j$
.
Now we can apply Lemma 7.2 as in the proof of part (1), except that now
![]() $\bar {\eta }$
may be strictly larger than
$\bar {\eta }$
may be strictly larger than
![]() $\pi _j^{-1}(\lambda )$
, to get a pair of
$\pi _j^{-1}(\lambda )$
, to get a pair of
![]() $\bar {\eta }$
-absolutely complementing trees
$\bar {\eta }$
-absolutely complementing trees
![]() $(\bar {S},\bar {T}) \in P_j[g_{j-1}]$
for
$(\bar {S},\bar {T}) \in P_j[g_{j-1}]$
for
![]() $A_j$
such that for every
$A_j$
such that for every
![]() $n < \omega $
, the restrictions
$n < \omega $
, the restrictions
![]() $\bar {S}\mathord {\restriction } n$
and
$\bar {S}\mathord {\restriction } n$
and
![]() $\bar {T} \mathord {\restriction } n$
to finite levels are in
$\bar {T} \mathord {\restriction } n$
to finite levels are in
![]() $P_j$
, and letting
$P_j$
, and letting
![]() $S = \bigcup _{n<\omega } \pi _j(\bar {S}\mathord {\restriction } n)$
and
$S = \bigcup _{n<\omega } \pi _j(\bar {S}\mathord {\restriction } n)$
and
![]() $T = \bigcup _{n<\omega } \pi _j(\bar {T}\mathord {\restriction } n)$
in
$T = \bigcup _{n<\omega } \pi _j(\bar {T}\mathord {\restriction } n)$
in
![]() $V_{\gamma }$
, the pair
$V_{\gamma }$
, the pair
![]() $(S,T)$
is
$(S,T)$
is
![]() $\eta $
-absolutely complementing where
$\eta $
-absolutely complementing where
![]() $\eta = \pi _j(\bar {\eta })$
. In particular, the pair
$\eta = \pi _j(\bar {\eta })$
. In particular, the pair
![]() $(S,T)$
is
$(S,T)$
is
![]() $\mathbb {R}$
-absolutely complementing. Moreover, the pair
$\mathbb {R}$
-absolutely complementing. Moreover, the pair
![]() $(S_{\omega }, T_{\omega }) = ( i_{j,\omega }^*(\bar {S}), i_{j,\omega }^*(\bar {T}))$
is
$(S_{\omega }, T_{\omega }) = ( i_{j,\omega }^*(\bar {S}), i_{j,\omega }^*(\bar {T}))$
is
![]() $\eta _\omega $
-absolutely complementing in
$\eta _\omega $
-absolutely complementing in
![]() $P_\omega [g_{j-1}]$
, so also in
$P_\omega [g_{j-1}]$
, so also in
![]() $P_\omega (\mathbb {R}^V)$
. It follows from our choice of
$P_\omega (\mathbb {R}^V)$
. It follows from our choice of
![]() $\eta _\omega $
that
$\eta _\omega $
that
![]() $(S_{\omega }, T_{\omega })$
is Z-absolutely complementing in
$(S_{\omega }, T_{\omega })$
is Z-absolutely complementing in
![]() $P_\omega (\mathbb {R}^V)$
.
$P_\omega (\mathbb {R}^V)$
.
We can use the pair of trees
![]() $(S_{\omega }, T_{\omega })$
to decide membership of x in the canonical expansion of A from the point of view of
$(S_{\omega }, T_{\omega })$
to decide membership of x in the canonical expansion of A from the point of view of
![]() $P_\omega (\mathbb {R}^V)$
, and use the pair of trees
$P_\omega (\mathbb {R}^V)$
, and use the pair of trees
![]() $(S,T)$
to decide membership of x in the canonical expansion of A from the point of view of V. As in the proof of part (1), we get the same answer in both cases because the realization map
$(S,T)$
to decide membership of x in the canonical expansion of A from the point of view of V. As in the proof of part (1), we get the same answer in both cases because the realization map
![]() $\pi _\omega $
takes branches of
$\pi _\omega $
takes branches of
![]() $S_{\omega }$
pointwise to branches of S and takes branches of
$S_{\omega }$
pointwise to branches of S and takes branches of
![]() $T_{\omega }$
pointwise to branches of T.
$T_{\omega }$
pointwise to branches of T.
The first part of Lemma 7.3 implies (assuming its hypotheses) that
![]() $\mathrm {uB}^{P_{\omega }(\mathbb {R}^{V})}$
is a Wadge-initial segment of
$\mathrm {uB}^{P_{\omega }(\mathbb {R}^{V})}$
is a Wadge-initial segment of
![]() $\mathrm {uB}^{V}$
. In conjunction with the second part, this implies that
$\mathrm {uB}^{V}$
. In conjunction with the second part, this implies that
Lemma 7.5 below is a stronger statement that implies this inclusion, phrased in terms of the following definition.
Definition 7.4. Given an ordinal
![]() $\alpha $
, we let
$\alpha $
, we let
![]() $\mathrm {uB} \mathord {\restriction } \alpha $
denote the collection of universally Baire sets of Wadge rank less than
$\mathrm {uB} \mathord {\restriction } \alpha $
denote the collection of universally Baire sets of Wadge rank less than
![]() $\alpha $
, and let
$\alpha $
, and let
![]() $F_\alpha $
be the class of all quadruples
$F_\alpha $
be the class of all quadruples
![]() $(A,\mathbb {P},p,\dot {x})$
in F for which
$(A,\mathbb {P},p,\dot {x})$
in F for which
![]() $A \in \mathrm {uB} \mathord {\restriction } \alpha $
.
$A \in \mathrm {uB} \mathord {\restriction } \alpha $
.
If
![]() $\alpha $
is at least the Wadge rank of the pointclass
$\alpha $
is at least the Wadge rank of the pointclass
![]() $\mathrm {uB}$
, then we simply have
$\mathrm {uB}$
, then we simply have
![]() $\mathrm {uB} \mathord {\restriction } \alpha = \mathrm {uB}$
. Using these definitions, we can state an immediate consequence of Lemma 7.3:
$\mathrm {uB} \mathord {\restriction } \alpha = \mathrm {uB}$
. Using these definitions, we can state an immediate consequence of Lemma 7.3:
Lemma 7.5. Let
![]() $\lambda $
be a limit of Woodin cardinals and a limit of strong cardinals, and let
$\lambda $
be a limit of Woodin cardinals and a limit of strong cardinals, and let
![]() $\gamma $
be a limit ordinal of cofinality greater than
$\gamma $
be a limit ordinal of cofinality greater than
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $P_{0}$
be a countable transitive set, and let
$P_{0}$
be a countable transitive set, and let
![]() $\pi _0 \colon P_0 \to V_{\gamma }$
be an elementary embedding with
$\pi _0 \colon P_0 \to V_{\gamma }$
be an elementary embedding with
![]() $\lambda \in \operatorname {\mathrm {ran}}(\pi _0)$
. Let
$\lambda \in \operatorname {\mathrm {ran}}(\pi _0)$
. Let
![]() $P_\omega $
be obtained from
$P_\omega $
be obtained from
![]() $P_0$
by a
$P_0$
by a
![]() $\pi _0$
-realizable
$\pi _0$
-realizable
![]() $\mathbb {R}$
-genericity iteration at
$\mathbb {R}$
-genericity iteration at
![]() $\lambda $
. Then we have
$\lambda $
. Then we have
where
![]() $\alpha $
is the Wadge rank of the pointclass
$\alpha $
is the Wadge rank of the pointclass
![]() $\mathrm {uB}^{P_\omega (\mathbb {R}^V)}$
and
$\mathrm {uB}^{P_\omega (\mathbb {R}^V)}$
and
![]() $\beta $
is the ordinal height of the model
$\beta $
is the ordinal height of the model
![]() $P_\omega $
.
$P_\omega $
.
8
 $\Sigma ^2_1$
reflection
$\Sigma ^2_1$
reflection
In this section, we prove the following
![]() $\Sigma ^2_1$
reflection result, following Steel’s stationary-tower-free proof [Reference Steel, Gao, Jackson and Zhang22] of
$\Sigma ^2_1$
reflection result, following Steel’s stationary-tower-free proof [Reference Steel, Gao, Jackson and Zhang22] of
![]() $\Sigma ^2_1$
reflection for the model
$\Sigma ^2_1$
reflection for the model
![]() $L(\mathbb {R}^*_G, \mathrm {Hom}^*_G)$
.
$L(\mathbb {R}^*_G, \mathrm {Hom}^*_G)$
.
Lemma 8.1. Let
![]() $\lambda $
be a limit of Woodin cardinals and a limit of strong cardinals, let
$\lambda $
be a limit of Woodin cardinals and a limit of strong cardinals, let
![]() $G \subseteq \mathrm {Col}(\omega ,\mathord {<}\lambda )$
be a V-generic filter, and let
$G \subseteq \mathrm {Col}(\omega ,\mathord {<}\lambda )$
be a V-generic filter, and let
![]() $\mathcal {M}$
be the model
$\mathcal {M}$
be the model
![]() $L^F(\mathbb {R}^*_G, \mathrm {Hom}^*_G)^{V(\mathbb {R}^*_G)}$
. For every sentence
$L^F(\mathbb {R}^*_G, \mathrm {Hom}^*_G)^{V(\mathbb {R}^*_G)}$
. For every sentence
![]() $\varphi $
, if there is a set of reals
$\varphi $
, if there is a set of reals
![]() $A\in \mathcal {M}$
such that
$A\in \mathcal {M}$
such that
![]() $(\mathrm {HC}^*_G,\mathord {\in },A) \models \varphi $
, then there is a set of reals
$(\mathrm {HC}^*_G,\mathord {\in },A) \models \varphi $
, then there is a set of reals
![]() $A \in \mathrm {Hom}_{\mathord {<}\lambda }^V$
such that
$A \in \mathrm {Hom}_{\mathord {<}\lambda }^V$
such that
![]() $(\mathrm {HC}^{V},\mathord {\in },A) \models \varphi $
.
$(\mathrm {HC}^{V},\mathord {\in },A) \models \varphi $
.
Recall that
![]() $\mathrm {Hom}^*_G = \mathrm {uB}^{V(\mathbb {R}^*_G)}$
, as
$\mathrm {Hom}^*_G = \mathrm {uB}^{V(\mathbb {R}^*_G)}$
, as
![]() $\lambda $
is a limit of strong cardinals, so we have an alternative characterization of
$\lambda $
is a limit of strong cardinals, so we have an alternative characterization of
![]() $\mathcal {M}$
that will be useful in this section:
$\mathcal {M}$
that will be useful in this section:
Supposing that the model
![]() $\mathcal {M}$
has a
$\mathcal {M}$
has a
![]() $\varphi $
-witness, the idea of the proof is to take a countable hull of some
$\varphi $
-witness, the idea of the proof is to take a countable hull of some
![]() $V_{\gamma }$
containing a
$V_{\gamma }$
containing a
![]() $\varphi $
-witness, and then to do an
$\varphi $
-witness, and then to do an
![]() $\mathbb {R}$
-genericity iteration of the hull to get a
$\mathbb {R}$
-genericity iteration of the hull to get a
![]() $\varphi $
-witness that is a subset of
$\varphi $
-witness that is a subset of
![]() $\mathbb {R}^V$
. More specifically, we start by fixing a limit ordinal
$\mathbb {R}^V$
. More specifically, we start by fixing a limit ordinal
![]() $\gamma $
of cofinality greater than
$\gamma $
of cofinality greater than
![]() $\lambda $
, so that every set of reals in
$\lambda $
, so that every set of reals in
![]() $\mathcal {M}$
is in
$\mathcal {M}$
is in
![]() $L_{\gamma }^{F}(\mathbb {R}^{*}_{G}, \mathrm {Hom}^{*}_{G})^{V_{\gamma }(\mathbb {R}^{*}_G)}$
. Considering an
$L_{\gamma }^{F}(\mathbb {R}^{*}_{G}, \mathrm {Hom}^{*}_{G})^{V_{\gamma }(\mathbb {R}^{*}_G)}$
. Considering an
![]() $\mathbb {R}$
-genericity iteration of the transitive collapse
$\mathbb {R}$
-genericity iteration of the transitive collapse
![]() $P_{0}$
of an elementary substructure of
$P_{0}$
of an elementary substructure of
![]() $V_{\gamma }$
, the elementarity of the corresponding map
$V_{\gamma }$
, the elementarity of the corresponding map
![]() $\pi _\omega \colon P_\omega \to V_{\gamma }$
(and the definability of forcing) gives a
$\pi _\omega \colon P_\omega \to V_{\gamma }$
(and the definability of forcing) gives a
![]() $\varphi $
-witness in the model
$\varphi $
-witness in the model
![]() $L^F(\mathbb {R},\mathrm {uB})^{P_\omega (\mathbb {R}^V)}$
, which is equal to the model
$L^F(\mathbb {R},\mathrm {uB})^{P_\omega (\mathbb {R}^V)}$
, which is equal to the model
![]() $L_\beta ^{F_\alpha }(\mathbb {R}, \mathrm {uB}\mathord {\restriction } \alpha )^V$
by Lemma 7.5, where
$L_\beta ^{F_\alpha }(\mathbb {R}, \mathrm {uB}\mathord {\restriction } \alpha )^V$
by Lemma 7.5, where
![]() $\alpha $
is the Wadge rank of the pointclass
$\alpha $
is the Wadge rank of the pointclass
![]() $\mathrm {uB}^{P_\omega (\mathbb {R}^V)}$
and
$\mathrm {uB}^{P_\omega (\mathbb {R}^V)}$
and
![]() $\beta $
is the ordinal height of the model
$\beta $
is the ordinal height of the model
![]() $P_\omega $
. In particular, there is a
$P_\omega $
. In particular, there is a
![]() $\varphi $
-witness in the model
$\varphi $
-witness in the model
![]() $L^F(\mathbb {R},\mathrm {uB})^V$
.
$L^F(\mathbb {R},\mathrm {uB})^V$
.
We will show that the least
![]() $\varphi $
-witness arising in this manner is in
$\varphi $
-witness arising in this manner is in
![]() $\mathrm {Hom}_{\mathord {<}\lambda }$
. To do this, we will consider different countable hulls
$\mathrm {Hom}_{\mathord {<}\lambda }$
. To do this, we will consider different countable hulls
![]() $P_0$
and different genericity iterations of these hulls giving rise to possibly different models of the form
$P_0$
and different genericity iterations of these hulls giving rise to possibly different models of the form
![]() $L^F(\mathbb {R}, \mathrm {uB})^{P_\omega (\mathbb {R}^V)}$
. We will see that the least
$L^F(\mathbb {R}, \mathrm {uB})^{P_\omega (\mathbb {R}^V)}$
. We will see that the least
![]() $\varphi $
-witness will be present in all of these models and will admit a uniform definition there in the sense of Lemma 6.6.
$\varphi $
-witness will be present in all of these models and will admit a uniform definition there in the sense of Lemma 6.6.
We consider two cases involving two different notions of least
![]() $\varphi $
-witness. The cases are exhaustive but not necessarily mutually exclusive; if they overlap, either one can be used.
$\varphi $
-witness. The cases are exhaustive but not necessarily mutually exclusive; if they overlap, either one can be used.
Case 1. For cofinally many elementary countable hulls
![]() $\pi _0 \colon P_0 \to V_{\gamma }$
with
$\pi _0 \colon P_0 \to V_{\gamma }$
with
![]() $\lambda \in \operatorname {\mathrm {ran}}(\pi _0)$
, every
$\lambda \in \operatorname {\mathrm {ran}}(\pi _0)$
, every
![]() $\pi _0$
-realizable
$\pi _0$
-realizable
![]() $\mathbb {R}$
-genericity iteration
$\mathbb {R}$
-genericity iteration
![]() $P_0\to P_\omega $
at
$P_0\to P_\omega $
at
![]() $\lambda $
has the property that
$\lambda $
has the property that
![]() $\mathrm {uB}^{P_\omega (\mathbb {R}^V)} = \mathrm {uB}^V$
.
$\mathrm {uB}^{P_\omega (\mathbb {R}^V)} = \mathrm {uB}^V$
.
In this case, let
![]() $\beta $
be the least ordinal such that the model
$\beta $
be the least ordinal such that the model
![]() $L_\beta ^F(\mathbb {R}, \mathrm {uB})^V$
has a
$L_\beta ^F(\mathbb {R}, \mathrm {uB})^V$
has a
![]() $\varphi $
-witness (which is less than
$\varphi $
-witness (which is less than
![]() $\gamma $
, as noted above). Take a set of reals
$\gamma $
, as noted above). Take a set of reals
![]() $C \in \mathrm {uB}^V$
such that this model contains a
$C \in \mathrm {uB}^V$
such that this model contains a
![]() $\varphi $
-witness that is ordinal-definable from the parameter C and the predicate F, and let
$\varphi $
-witness that is ordinal-definable from the parameter C and the predicate F, and let
![]() $A \in L_\beta ^F(\mathbb {R}, \mathrm {uB})^V$
be the least such
$A \in L_\beta ^F(\mathbb {R}, \mathrm {uB})^V$
be the least such
![]() $\varphi $
-witness in the canonical well-ordering of sets ordinal definable over
$\varphi $
-witness in the canonical well-ordering of sets ordinal definable over
![]() $L^{F}_{\beta }(\mathbb {R}, \mathrm {uB})^{V}$
from C and F.
$L^{F}_{\beta }(\mathbb {R}, \mathrm {uB})^{V}$
from C and F.
Take a countable hull
![]() $\pi _0 \colon P_0 \to V_{\gamma }$
such that
$\pi _0 \colon P_0 \to V_{\gamma }$
such that
![]() $(C, \lambda ) \in \operatorname {\mathrm {ran}}(\pi _0)$
, and for every
$(C, \lambda ) \in \operatorname {\mathrm {ran}}(\pi _0)$
, and for every
![]() $\pi _0$
-realizable
$\pi _0$
-realizable
![]() $\mathbb {R}$
-genericity iteration
$\mathbb {R}$
-genericity iteration
![]() $P_0\to P_\omega $
at
$P_0\to P_\omega $
at
![]() $\lambda $
, we have
$\lambda $
, we have
![]() $\mathrm {uB}^{P_\omega (\mathbb {R}^V)} = \mathrm {uB}^V$
. For every such
$\mathrm {uB}^{P_\omega (\mathbb {R}^V)} = \mathrm {uB}^V$
. For every such
![]() $\mathbb {R}$
-genericity iteration, we have
$\mathbb {R}$
-genericity iteration, we have
![]() $\beta \in P_\omega $
by the minimality of
$\beta \in P_\omega $
by the minimality of
![]() $\beta $
; otherwise, the model
$\beta $
; otherwise, the model
![]() $L^F(\mathbb {R}, \mathrm {uB})^{P_\omega (\mathbb {R}^V)}$
would not be tall enough to reach a
$L^F(\mathbb {R}, \mathrm {uB})^{P_\omega (\mathbb {R}^V)}$
would not be tall enough to reach a
![]() $\varphi $
-witness (by Lemma 7.5), violating the elementarity of
$\varphi $
-witness (by Lemma 7.5), violating the elementarity of
![]() $\pi _\omega $
. Moreover, the set C is in
$\pi _\omega $
. Moreover, the set C is in
![]() $P_\omega (\mathbb {R}^V)$
because it is the canonical expansion of the set
$P_\omega (\mathbb {R}^V)$
because it is the canonical expansion of the set
![]() $\pi _\omega ^{-1}(C) \in P_\omega $
, as in Remark 6.4.
$\pi _\omega ^{-1}(C) \in P_\omega $
, as in Remark 6.4.
For every
![]() $\pi _0$
-realizable
$\pi _0$
-realizable
![]() $\mathbb {R}$
-genericity iteration
$\mathbb {R}$
-genericity iteration
![]() $P_0\to P_\omega $
at
$P_0\to P_\omega $
at
![]() $\lambda $
, the ordinal
$\lambda $
, the ordinal
![]() $\beta $
is definable in
$\beta $
is definable in
![]() $P_\omega (\mathbb {R}^V)$
as the least ordinal such that the model
$P_\omega (\mathbb {R}^V)$
as the least ordinal such that the model
![]() $L_\beta ^F(\mathbb {R}, \mathrm {uB})^{P_\omega (\mathbb {R}^V)}$
contains a
$L_\beta ^F(\mathbb {R}, \mathrm {uB})^{P_\omega (\mathbb {R}^V)}$
contains a
![]() $\varphi $
-witness, and in turn, the least
$\varphi $
-witness, and in turn, the least
![]() $\varphi $
-witness A is definable from C in the model
$\varphi $
-witness A is definable from C in the model
![]() $L_\beta ^F(\mathbb {R}, \mathrm {uB})^{P_\omega (\mathbb {R}^V)}$
by the same definition as in the model
$L_\beta ^F(\mathbb {R}, \mathrm {uB})^{P_\omega (\mathbb {R}^V)}$
by the same definition as in the model
![]() $L_\beta ^F(\mathbb {R}, \mathrm {uB})^V$
, which is the same model. This implies that
$L_\beta ^F(\mathbb {R}, \mathrm {uB})^V$
, which is the same model. This implies that
![]() $A \in \mathrm {Hom}_{\mathord {<}\lambda }^V$
by Lemma 6.6 as desired.
$A \in \mathrm {Hom}_{\mathord {<}\lambda }^V$
by Lemma 6.6 as desired.
Case 2. For cofinally many sufficiently elementary countable hulls
![]() $\pi _0 \colon P_0 \to V_{\gamma }$
with
$\pi _0 \colon P_0 \to V_{\gamma }$
with
![]() $\lambda \in \operatorname {\mathrm {ran}}(\pi _0)$
, there is a
$\lambda \in \operatorname {\mathrm {ran}}(\pi _0)$
, there is a
![]() $\pi _0$
-realizable
$\pi _0$
-realizable
![]() $\mathbb {R}$
-genericity iteration
$\mathbb {R}$
-genericity iteration
![]() $P_0\to P_\omega $
at
$P_0\to P_\omega $
at
![]() $\lambda $
such that
$\lambda $
such that
![]() $\mathrm {uB}^{P_\omega (\mathbb {R}^V)} \subsetneq \mathrm {uB}^V$
.
$\mathrm {uB}^{P_\omega (\mathbb {R}^V)} \subsetneq \mathrm {uB}^V$
.
In this case, we will need the following claim, which says that we can put an upper bound on the pointclass necessary to construct a
![]() $\varphi $
-witness.
$\varphi $
-witness.
Claim 8.2. Under the assumption of Case 2, there is a set of reals
![]() $D \in \mathrm {uB}^V$
such that, letting
$D \in \mathrm {uB}^V$
such that, letting
![]() $D^*$
denote the canonical expansion
$D^*$
denote the canonical expansion
![]() $D^{V(\mathbb {R}^*_G)}$
and letting
$D^{V(\mathbb {R}^*_G)}$
and letting
![]() $\alpha ^*$
denote the Wadge rank of
$\alpha ^*$
denote the Wadge rank of
![]() $D^*$
in
$D^*$
in
![]() $V(\mathbb {R}^*_G)$
, the model
$V(\mathbb {R}^*_G)$
, the model
contains a
![]() $\varphi $
-witness.
$\varphi $
-witness.
Proof. Take an elementary countable hull
![]() $\pi _0 \colon P_0 \to V_{\gamma }$
with
$\pi _0 \colon P_0 \to V_{\gamma }$
with
![]() $\lambda \in \operatorname {\mathrm {ran}}(\pi _0)$
, and take a
$\lambda \in \operatorname {\mathrm {ran}}(\pi _0)$
, and take a
![]() $\pi _0$
-realizable
$\pi _0$
-realizable
![]() $\mathbb {R}$
-genericity iteration
$\mathbb {R}$
-genericity iteration
![]() $P_0\to P_\omega $
at
$P_0\to P_\omega $
at
![]() $\lambda $
such that
$\lambda $
such that
![]() $\mathrm {uB}^{P_\omega (\mathbb {R}^V)} \subsetneq \mathrm {uB}^V$
. Then by Lemma 7.5 and the elementarity of the realization map
$\mathrm {uB}^{P_\omega (\mathbb {R}^V)} \subsetneq \mathrm {uB}^V$
. Then by Lemma 7.5 and the elementarity of the realization map
![]() $\pi _\omega \colon P_\omega \to V_{\gamma }$
, there is a
$\pi _\omega \colon P_\omega \to V_{\gamma }$
, there is a
![]() $\varphi $
-witness in the model
$\varphi $
-witness in the model
![]() $L^{F_\alpha }_\beta (\mathbb {R}, \mathrm {uB} \mathord {\restriction } \alpha )^V$
, where
$L^{F_\alpha }_\beta (\mathbb {R}, \mathrm {uB} \mathord {\restriction } \alpha )^V$
, where
![]() $\alpha $
is the Wadge rank of the pointclass
$\alpha $
is the Wadge rank of the pointclass
![]() $\mathrm {uB}^{P_\omega (\mathbb {R}^V)}$
and
$\mathrm {uB}^{P_\omega (\mathbb {R}^V)}$
and
![]() $\beta = \mathrm {Ord}^{P_\omega }$
.
$\beta = \mathrm {Ord}^{P_\omega }$
.
Take a set of reals
![]() $D \in \mathrm {uB}^V$
of Wadge rank
$D \in \mathrm {uB}^V$
of Wadge rank
![]() $\alpha $
, take a sufficiently elementary countable hull
$\alpha $
, take a sufficiently elementary countable hull
![]() $\pi _0^{\prime } \colon P_0^{\prime } \to V_{\gamma }$
with
$\pi _0^{\prime } \colon P_0^{\prime } \to V_{\gamma }$
with
![]() $(D, \lambda ) \in \operatorname {\mathrm {ran}}(\pi _0^{\prime })$
, and take a
$(D, \lambda ) \in \operatorname {\mathrm {ran}}(\pi _0^{\prime })$
, and take a
![]() $\pi _0^{\prime }$
-realizable
$\pi _0^{\prime }$
-realizable
![]() $\mathbb {R}$
-genericity iteration
$\mathbb {R}$
-genericity iteration
![]() $P_0^{\prime }\to P_\omega ^{\prime }$
at
$P_0^{\prime }\to P_\omega ^{\prime }$
at
![]() $\lambda $
such that
$\lambda $
such that
![]() $\mathrm {uB}^{P_\omega ^{\prime }(\mathbb {R}^V)} \subsetneq \mathrm {uB}^V$
.
$\mathrm {uB}^{P_\omega ^{\prime }(\mathbb {R}^V)} \subsetneq \mathrm {uB}^V$
.
The model
![]() $P_\omega ^{\prime }(\mathbb {R}^V)$
sees the set D as the canonical expansion of
$P_\omega ^{\prime }(\mathbb {R}^V)$
sees the set D as the canonical expansion of
![]() $\pi _\omega ^{-1}(D)$
, and it sees the pointclass
$\pi _\omega ^{-1}(D)$
, and it sees the pointclass
![]() $\mathrm {uB}^V \mathord {\restriction } \alpha $
as its collection of
$\mathrm {uB}^V \mathord {\restriction } \alpha $
as its collection of
![]() $\mathrm {uB}$
sets of Wadge rank less than that of D. If we have
$\mathrm {uB}$
sets of Wadge rank less than that of D. If we have
![]() $\mathrm {Ord}^{P_\omega } \le \mathrm {Ord}^{P_\omega ^{\prime }}$
, then the model
$\mathrm {Ord}^{P_\omega } \le \mathrm {Ord}^{P_\omega ^{\prime }}$
, then the model
![]() $P_\omega ^{\prime }(\mathbb {R}^V)$
is tall enough to see that a
$P_\omega ^{\prime }(\mathbb {R}^V)$
is tall enough to see that a
![]() $\varphi $
-witness can be built from
$\varphi $
-witness can be built from
![]() $\mathrm {uB}^V \mathord {\restriction } \alpha $
using the F predicate, and the claim follows from the elementarity of the realization map
$\mathrm {uB}^V \mathord {\restriction } \alpha $
using the F predicate, and the claim follows from the elementarity of the realization map
![]() $\pi _\omega ^{\prime } \colon P_\omega ^{\prime } \to V_{\gamma }$
.
$\pi _\omega ^{\prime } \colon P_\omega ^{\prime } \to V_{\gamma }$
.
However, if
![]() $\mathrm {Ord}^{P_\omega }> \mathrm {Ord}^{P_\omega ^{\prime }}$
, then we can repeat this procedure with the hull
$\mathrm {Ord}^{P_\omega }> \mathrm {Ord}^{P_\omega ^{\prime }}$
, then we can repeat this procedure with the hull
![]() $\pi _0^{\prime } \colon P_0^{\prime } \to V_{\gamma }$
in place of the hull
$\pi _0^{\prime } \colon P_0^{\prime } \to V_{\gamma }$
in place of the hull
![]() $\pi _0 \colon P_0 \to V_{\gamma }$
. (This is why we made sure to take the second hull with
$\pi _0 \colon P_0 \to V_{\gamma }$
. (This is why we made sure to take the second hull with
![]() $\mathrm {uB}^{P_\omega ^{\prime }(\mathbb {R}^V)} \subsetneq \mathrm {uB}^V$
also.) Repeating this procedure for
$\mathrm {uB}^{P_\omega ^{\prime }(\mathbb {R}^V)} \subsetneq \mathrm {uB}^V$
also.) Repeating this procedure for
![]() $\omega $
many steps, either at some step, we get a set
$\omega $
many steps, either at some step, we get a set
![]() $D \in \mathrm {uB}^V$
satisfying the claim, or else we get an infinite decreasing sequence of ordinals
$D \in \mathrm {uB}^V$
satisfying the claim, or else we get an infinite decreasing sequence of ordinals
![]() $\mathrm {Ord}^{P_\omega }> \mathrm {Ord}^{P_\omega ^{\prime }} > \mathrm {Ord}^{P_\omega ^{\prime \prime }} > \cdots $
, a contradiction.
$\mathrm {Ord}^{P_\omega }> \mathrm {Ord}^{P_\omega ^{\prime }} > \mathrm {Ord}^{P_\omega ^{\prime \prime }} > \cdots $
, a contradiction.
Now we can proceed as in Case 1. Let
![]() $D \in \mathrm {uB}^V$
be a set as in the claim. Taking any countable hull
$D \in \mathrm {uB}^V$
be a set as in the claim. Taking any countable hull
![]() $\pi _0 : P_0 \to V_{\gamma }$
with
$\pi _0 : P_0 \to V_{\gamma }$
with
![]() $D \in \operatorname {\mathrm {ran}}(\pi _0)$
and taking any genericity iterate
$D \in \operatorname {\mathrm {ran}}(\pi _0)$
and taking any genericity iterate
![]() $P_0 \to P_\omega $
of this hull, by the elementarity of the factor map
$P_0 \to P_\omega $
of this hull, by the elementarity of the factor map
![]() $\pi _\omega $
and the proof of Lemma 7.5, we see that there is a
$\pi _\omega $
and the proof of Lemma 7.5, we see that there is a
![]() $\varphi $
-witness in the model
$\varphi $
-witness in the model
![]() $L_\beta ^{F_\alpha }(\mathbb {R}, \mathrm {uB} \mathord {\restriction } \alpha )^V$
for some ordinal
$L_\beta ^{F_\alpha }(\mathbb {R}, \mathrm {uB} \mathord {\restriction } \alpha )^V$
for some ordinal
![]() $\beta < \gamma $
, where
$\beta < \gamma $
, where
![]() $\alpha $
is the Wadge rank of D. Let
$\alpha $
is the Wadge rank of D. Let
![]() $\beta $
be the least ordinal such that there is a
$\beta $
be the least ordinal such that there is a
![]() $\varphi $
-witness in the model
$\varphi $
-witness in the model
![]() $L_\beta ^{F_\alpha }(\mathbb {R}, \mathrm {uB} \mathord {\restriction } \alpha )^V$
.
$L_\beta ^{F_\alpha }(\mathbb {R}, \mathrm {uB} \mathord {\restriction } \alpha )^V$
.
Take a set of reals
![]() $C \in \mathrm {uB}^V \mathord {\restriction } \alpha $
such that the model
$C \in \mathrm {uB}^V \mathord {\restriction } \alpha $
such that the model
![]() $L_\beta ^{F_\alpha }(\mathbb {R}, \mathrm {uB} \mathord {\restriction } \alpha )^V$
has a
$L_\beta ^{F_\alpha }(\mathbb {R}, \mathrm {uB} \mathord {\restriction } \alpha )^V$
has a
![]() $\varphi $
-witness that is ordinal-definable from the parameter C and the predicate F, and let
$\varphi $
-witness that is ordinal-definable from the parameter C and the predicate F, and let
![]() $A \in L_\beta ^{F_\alpha }(\mathbb {R}, \mathrm {uB} \mathord {\restriction } \alpha )^V$
be the least such
$A \in L_\beta ^{F_\alpha }(\mathbb {R}, \mathrm {uB} \mathord {\restriction } \alpha )^V$
be the least such
![]() $\varphi $
-witness in the canonical well-ordering relative to C.
$\varphi $
-witness in the canonical well-ordering relative to C.
Take a countable hull
![]() $\pi _0 \colon P_0 \to V_{\gamma }$
with
$\pi _0 \colon P_0 \to V_{\gamma }$
with
![]() $(\lambda ,C,D) \in \operatorname {\mathrm {ran}}(\pi _0)$
. For every
$(\lambda ,C,D) \in \operatorname {\mathrm {ran}}(\pi _0)$
. For every
![]() $\mathbb {R}$
-genericity iteration
$\mathbb {R}$
-genericity iteration
![]() $P_0 \to P_\omega $
, we have
$P_0 \to P_\omega $
, we have
![]() $\beta \in P_\omega $
by the minimality of
$\beta \in P_\omega $
by the minimality of
![]() $\beta $
; otherwise, the model
$\beta $
; otherwise, the model
![]() $L^{F_\alpha }(\mathbb {R}, \mathrm {uB} \mathord {\restriction } \alpha )^{P_\omega (\mathbb {R}^V)}$
would not be tall enough to reach a
$L^{F_\alpha }(\mathbb {R}, \mathrm {uB} \mathord {\restriction } \alpha )^{P_\omega (\mathbb {R}^V)}$
would not be tall enough to reach a
![]() $\varphi $
-witness, violating the elementarity of
$\varphi $
-witness, violating the elementarity of
![]() $\pi _\omega $
.
$\pi _\omega $
.
For every such genericity iteration, the ordinal
![]() $\alpha $
is definable from the set D in
$\alpha $
is definable from the set D in
![]() $P_\omega (\mathbb {R}^V)$
as its Wadge rank, the ordinal
$P_\omega (\mathbb {R}^V)$
as its Wadge rank, the ordinal
![]() $\beta $
is definable from
$\beta $
is definable from
![]() $\alpha $
in
$\alpha $
in
![]() $P_\omega (\mathbb {R}^V)$
as the least ordinal such that the model
$P_\omega (\mathbb {R}^V)$
as the least ordinal such that the model
![]() $L_\beta ^{F_\alpha }(\mathbb {R}, \mathrm {uB} \mathord {\restriction } \alpha )^{P_\omega (\mathbb {R}^V)}$
contains a
$L_\beta ^{F_\alpha }(\mathbb {R}, \mathrm {uB} \mathord {\restriction } \alpha )^{P_\omega (\mathbb {R}^V)}$
contains a
![]() $\varphi $
-witness, and in turn, the least
$\varphi $
-witness, and in turn, the least
![]() $\varphi $
-witness A is definable from C in the model
$\varphi $
-witness A is definable from C in the model
![]() $L_\beta ^{F_\alpha }(\mathbb {R}, \mathrm {uB} \mathord {\restriction } \alpha )^{P_\omega (\mathbb {R}^V)}$
by the same definition as in the model
$L_\beta ^{F_\alpha }(\mathbb {R}, \mathrm {uB} \mathord {\restriction } \alpha )^{P_\omega (\mathbb {R}^V)}$
by the same definition as in the model
![]() $L_\beta ^{F_\alpha }(\mathbb {R}, \mathrm {uB} \mathord {\restriction } \alpha )^V$
,which is the same model. This implies that
$L_\beta ^{F_\alpha }(\mathbb {R}, \mathrm {uB} \mathord {\restriction } \alpha )^V$
,which is the same model. This implies that
![]() $A \in \mathrm {Hom}_{\mathord {<}\lambda }$
by Lemma 6.6 as desired.
$A \in \mathrm {Hom}_{\mathord {<}\lambda }$
by Lemma 6.6 as desired.
9 Suslin sets in the derived model
This section is mostly an exposition of the following theorem regarding the derived model
![]() $D(V,\lambda ,G)$
, which was defined in Remark 5.4. A proof of the corresponding theorem (also due to Woodin) for the old dervied model
$D(V,\lambda ,G)$
, which was defined in Remark 5.4. A proof of the corresponding theorem (also due to Woodin) for the old dervied model
![]() $L(\mathbb {R}^*_G, \mathrm {Hom}^*_G)$
can be found in Steel [Reference Steel23, Section 9].
$L(\mathbb {R}^*_G, \mathrm {Hom}^*_G)$
can be found in Steel [Reference Steel23, Section 9].
Theorem 9.1 (Woodin).
Let
![]() $\lambda $
be a limit of Woodin cardinals and of
$\lambda $
be a limit of Woodin cardinals and of
![]() $\mathord {<}\lambda $
-strong cardinals. Let
$\mathord {<}\lambda $
-strong cardinals. Let
![]() $G \subseteq \mathrm {Col}(\omega ,\mathord {<}\lambda )$
be a V-generic filter. Then the derived model
$G \subseteq \mathrm {Col}(\omega ,\mathord {<}\lambda )$
be a V-generic filter. Then the derived model
![]() $D(V,\lambda ,G)$
satisfies the statement that every set of reals is Suslin.
$D(V,\lambda ,G)$
satisfies the statement that every set of reals is Suslin.
Remark 9.2. As shown at the beginning of Section 5,
![]() $\mathrm {Hom}^{*}_{G}$
is equal to the set of subsets of
$\mathrm {Hom}^{*}_{G}$
is equal to the set of subsets of
![]() $\mathbb {R}^{*}_{G}$
in
$\mathbb {R}^{*}_{G}$
in
![]() $V(\mathbb {R}^{*}_{G})$
which are Suslin and co-Suslin in
$V(\mathbb {R}^{*}_{G})$
which are Suslin and co-Suslin in
![]() $V(\mathbb {R}^{*}_{G})$
. It follows from Theorem 9.1 then that (assuming its hypotheses) every set of reals in
$V(\mathbb {R}^{*}_{G})$
. It follows from Theorem 9.1 then that (assuming its hypotheses) every set of reals in
![]() $D(V, \lambda , G)$
is in
$D(V, \lambda , G)$
is in
![]() $\mathrm {Hom}^{*}_{G}$
, so
$\mathrm {Hom}^{*}_{G}$
, so
![]() $L(\mathbb {R}^{*}_{G}, \mathrm {Hom}^{*}_{G}) = D(V, \lambda , G)$
.
$L(\mathbb {R}^{*}_{G}, \mathrm {Hom}^{*}_{G}) = D(V, \lambda , G)$
.
The proof we give for Theorem 9.1 is based on one by Steel,Footnote
2
with a couple of modifications. One modification is that we separate the argument into two parts. The first part is Lemma 9.5 below, which uses only the assumption that
![]() $\lambda $
is a limit of
$\lambda $
is a limit of
![]() $\mathord {<}\lambda $
-strong cardinals, and which may be of independent interest. The remainder of the argument will use (in addition to the conclusion of Lemma 9.5) only the assumption that
$\mathord {<}\lambda $
-strong cardinals, and which may be of independent interest. The remainder of the argument will use (in addition to the conclusion of Lemma 9.5) only the assumption that
![]() $\lambda $
is a limit of Woodin cardinals. This large cardinal hypothesis implies that
$\lambda $
is a limit of Woodin cardinals. This large cardinal hypothesis implies that
![]() $\mathrm {Hom}^{*}_{G} \subseteq \Gamma _{+}$
(by the version of the derived model theorem which appears as Theorem 7.1 in [Reference Steel23]) and that
$\mathrm {Hom}^{*}_{G} \subseteq \Gamma _{+}$
(by the version of the derived model theorem which appears as Theorem 7.1 in [Reference Steel23]) and that
![]() $D(V, \lambda , G)$
satisfies
$D(V, \lambda , G)$
satisfies
![]() $\mathsf {AD}^{+}$
, which is the first part of Theorem 31 of [Reference Woodin24].
$\mathsf {AD}^{+}$
, which is the first part of Theorem 31 of [Reference Woodin24].
The second modification is that we consider Suslin-norms (as defined below) rather than Suslin wellfounded relations as in Steel’s proof. This seems to be necessary in order to split up the proof as we have done.
Given a norm
![]() $\varphi $
on a set of reals A, the code of
$\varphi $
on a set of reals A, the code of
![]() $\varphi $
is the pair of binary relations
$\varphi $
is the pair of binary relations
![]() $(R_\le , R_<)$
defined by
$(R_\le , R_<)$
defined by
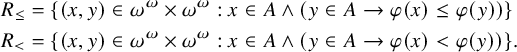 $$ \begin{align*} R_\le &= \{(x,y) \in \omega^\omega \times \omega^\omega : x \in A \wedge (y \in A \rightarrow \varphi(x) \le \varphi(y))\}\\ R_< &= \{(x,y) \in \omega^\omega \times \omega^\omega : x \in A \wedge (y \in A \rightarrow \varphi(x) < \varphi(y))\}. \end{align*} $$
$$ \begin{align*} R_\le &= \{(x,y) \in \omega^\omega \times \omega^\omega : x \in A \wedge (y \in A \rightarrow \varphi(x) \le \varphi(y))\}\\ R_< &= \{(x,y) \in \omega^\omega \times \omega^\omega : x \in A \wedge (y \in A \rightarrow \varphi(x) < \varphi(y))\}. \end{align*} $$
Note that the property of being a code for some norm on A can be expressed as the conjunction of the following conditions:
-
•
 $R_\le \cap (A \times A)$
is a prewellordering on A,
$R_\le \cap (A \times A)$
is a prewellordering on A, -
•
 $R_< \cap (A \times A)$
is the strict part of this prewellordering,
$R_< \cap (A \times A)$
is the strict part of this prewellordering, -
•
 $(A \times \neg A) \subseteq R_\le \subseteq (A \times \omega ^\omega )$
and
$(A \times \neg A) \subseteq R_\le \subseteq (A \times \omega ^\omega )$
and -
•
 $(A \times \neg A) \subseteq R_< \subseteq (A \times \omega ^\omega )$
.
$(A \times \neg A) \subseteq R_< \subseteq (A \times \omega ^\omega )$
.
Two norms on a set A are said to be equivalent if their codes are the same. Every norm is equivalent to a unique regular norm, a norm whose range is an ordinal. An initial segment of a set A under a norm
![]() $\varphi $
on A is a set of the form
$\varphi $
on A is a set of the form
![]() $\{x \in A : \varphi (x) < \xi \}$
for some ordinal
$\{x \in A : \varphi (x) < \xi \}$
for some ordinal
![]() $\xi $
.
$\xi $
.
We will need the following fact about extending norms. The proof is standard and is left to the reader.
Lemma 9.3. Let
![]() $\varphi $
be a regular norm on a set of reals A, and let
$\varphi $
be a regular norm on a set of reals A, and let
![]() $\varphi ^{\prime }$
be a regular norm on a set of reals
$\varphi ^{\prime }$
be a regular norm on a set of reals
![]() $A^{\prime }$
. Let
$A^{\prime }$
. Let
![]() $(R_\le , R_<)$
and
$(R_\le , R_<)$
and
![]() $(R^{\prime }_\le , R^{\prime }_<)$
denote the pairs of relations coding
$(R^{\prime }_\le , R^{\prime }_<)$
denote the pairs of relations coding
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi ^{\prime }$
, respectively. If
$\varphi ^{\prime }$
, respectively. If
![]() $A \subseteq A^{\prime }, \ R_\le \subseteq R_\le ^{\prime }$
and
$A \subseteq A^{\prime }, \ R_\le \subseteq R_\le ^{\prime }$
and
![]() $R_< \subseteq R_<^{\prime }$
, then the set A is an initial segment of the set
$R_< \subseteq R_<^{\prime }$
, then the set A is an initial segment of the set
![]() $A^{\prime }$
under its norm
$A^{\prime }$
under its norm
![]() $\varphi ^{\prime }$
, and we have
$\varphi ^{\prime }$
, and we have
![]() $\varphi = \varphi ^{\prime } \mathord {\restriction } A$
.
$\varphi = \varphi ^{\prime } \mathord {\restriction } A$
.
If
![]() $\Gamma $
is a pointclass, a
$\Gamma $
is a pointclass, a
![]() $\Gamma $
-norm on a set of reals
$\Gamma $
-norm on a set of reals
![]() $A \in \Gamma $
is a norm
$A \in \Gamma $
is a norm
![]() $\varphi $
on A with the property that its code
$\varphi $
on A with the property that its code
![]() $(R_\le ,R_<)$
is in
$(R_\le ,R_<)$
is in
![]() $\Gamma $
, meaning that both relations
$\Gamma $
, meaning that both relations
![]() $R_\le $
and
$R_\le $
and
![]() $R_<$
are continuous preimages of sets in
$R_<$
are continuous preimages of sets in
![]() $\Gamma $
. This is equivalent to the usual definition [Reference Moschovakis15, p. 153] if
$\Gamma $
. This is equivalent to the usual definition [Reference Moschovakis15, p. 153] if
![]() $\Gamma $
is an adequate pointclass. All of the pointclasses that we will consider are adequate.
$\Gamma $
is an adequate pointclass. All of the pointclasses that we will consider are adequate.
Remark 9.4. For pointclasses
![]() $\Gamma $
closed under unions, intersections and continuous preimages (as all the pointclasses we consider are), if
$\Gamma $
closed under unions, intersections and continuous preimages (as all the pointclasses we consider are), if
![]() $\varphi ^{\prime }$
is a
$\varphi ^{\prime }$
is a
![]() $\Gamma $
-norm on a set
$\Gamma $
-norm on a set
![]() $A^{\prime } \in \Gamma $
, then every proper initial segment A of
$A^{\prime } \in \Gamma $
, then every proper initial segment A of
![]() $A^{\prime }$
under
$A^{\prime }$
under
![]() $\varphi ^{\prime }$
is in
$\varphi ^{\prime }$
is in
![]() $\Delta = \Gamma \cap \check {\Gamma }$
, and the corresponding restricted norm
$\Delta = \Gamma \cap \check {\Gamma }$
, and the corresponding restricted norm
![]() $\varphi ^{\prime } \mathord {\restriction } A$
is a
$\varphi ^{\prime } \mathord {\restriction } A$
is a
![]() $\Delta $
-norm (see Remark 4.13 of [Reference Larson11], for instance).
$\Delta $
-norm (see Remark 4.13 of [Reference Larson11], for instance).
By a Suslin-norm, we mean a
![]() $\Gamma $
-norm where
$\Gamma $
-norm where
![]() $\Gamma $
is the pointclass of Suslin sets. Given a cardinal
$\Gamma $
is the pointclass of Suslin sets. Given a cardinal
![]() $\lambda $
, a
$\lambda $
, a
![]() $\mathrm {uB}_{\lambda }$
-norm is a
$\mathrm {uB}_{\lambda }$
-norm is a
![]() $\Gamma $
-norm where
$\Gamma $
-norm where
![]() $\Gamma $
is the pointclass of
$\Gamma $
is the pointclass of
![]() $\lambda $
-universally Baire sets.
$\lambda $
-universally Baire sets.
For a pointset R, a
![]() $\mathrm {pos}\Sigma ^1_1(R)$
-statement is one of the form
$\mathrm {pos}\Sigma ^1_1(R)$
-statement is one of the form
where Q is a
![]() $\Sigma ^1_1$
formula and we think of a real y as coding a sequence of reals
$\Sigma ^1_1$
formula and we think of a real y as coding a sequence of reals
![]() $(y)_0,(y)_1,(y)_2,\ldots $
in some recursive way (see, for instance, Moschovakis [Reference Moschovakis15, Lemma 7D.7] or page 21 of [Reference Larson11]). For pointsets
$(y)_0,(y)_1,(y)_2,\ldots $
in some recursive way (see, for instance, Moschovakis [Reference Moschovakis15, Lemma 7D.7] or page 21 of [Reference Larson11]). For pointsets
![]() $R_1,\ldots ,R_n$
, we define
$R_1,\ldots ,R_n$
, we define
![]() $\mathrm {pos}\Sigma ^1_1(R_1,\ldots ,R_n)$
as
$\mathrm {pos}\Sigma ^1_1(R_1,\ldots ,R_n)$
as
![]() $\mathrm {pos}\Sigma ^1_1(R)$
, where R is the disjoint union of the sets
$\mathrm {pos}\Sigma ^1_1(R)$
, where R is the disjoint union of the sets
![]() $R_1,\ldots ,R_n$
.
$R_1,\ldots ,R_n$
.
If R is a binary relation, then the statement that R is ill-founded can be expressed by a
![]() $\mathrm {pos}\Sigma ^1_1(R)$
statement, and the statement that R is not a prewellordering can be expressed by a
$\mathrm {pos}\Sigma ^1_1(R)$
statement, and the statement that R is not a prewellordering can be expressed by a
![]() $\mathrm {pos}\Sigma ^1_1(R,\neg R)$
statement. In addition, one can say (quite trivially) that
$\mathrm {pos}\Sigma ^1_1(R,\neg R)$
statement. In addition, one can say (quite trivially) that
![]() $A \cap B \ne \emptyset $
with a
$A \cap B \ne \emptyset $
with a
![]() $\mathrm {pos}\Sigma ^1_1(A,B)$
statement.
$\mathrm {pos}\Sigma ^1_1(A,B)$
statement.
For any trees
![]() $T_1,\ldots ,T_n$
, by
$T_1,\ldots ,T_n$
, by
![]() $\mathrm {pos}\Sigma ^1_1(\text {p}[T_1],\ldots ,\text {p}[T_n])$
generic absoluteness, we mean the fact that, for any generic extension
$\mathrm {pos}\Sigma ^1_1(\text {p}[T_1],\ldots ,\text {p}[T_n])$
generic absoluteness, we mean the fact that, for any generic extension
![]() $V[g]$
, any given
$V[g]$
, any given
![]() $\mathrm {pos}\Sigma ^1_1$
statement about the sets
$\mathrm {pos}\Sigma ^1_1$
statement about the sets
![]() $\mathrm {p}[T_1]^{V[g]},\ldots ,\mathrm {p}[T_n]^{V[g]}$
holds in
$\mathrm {p}[T_1]^{V[g]},\ldots ,\mathrm {p}[T_n]^{V[g]}$
holds in
![]() $V[g]$
if and only if the corresponding
$V[g]$
if and only if the corresponding
![]() $\mathrm {pos}\Sigma ^1_1$
statement about the sets
$\mathrm {pos}\Sigma ^1_1$
statement about the sets
![]() $\mathrm {p}[T_1],\ldots ,\mathrm {p}[T_n]$
holds in V. This fact is easily proved using the absoluteness of wellfoundedness for a certain tree built from
$\mathrm {p}[T_1],\ldots ,\mathrm {p}[T_n]$
holds in V. This fact is easily proved using the absoluteness of wellfoundedness for a certain tree built from
![]() $T_1,\ldots ,T_n$
and a tree for a
$T_1,\ldots ,T_n$
and a tree for a
![]() $\mathrm {pos}\Sigma ^1_1$
set. (There is nothing special about the case of generic extensions versus arbitrary outer models here, but it is the only case we will need.) This generic absoluteness property encompasses many of the common absoluteness arguments involving trees. It can be used to show, for example, that if R is a universally Baire wellfounded relation (or prewellordering), then the canonical expansion
$\mathrm {pos}\Sigma ^1_1$
set. (There is nothing special about the case of generic extensions versus arbitrary outer models here, but it is the only case we will need.) This generic absoluteness property encompasses many of the common absoluteness arguments involving trees. It can be used to show, for example, that if R is a universally Baire wellfounded relation (or prewellordering), then the canonical expansion
![]() $R^{V[g]}$
is a universally Baire wellfounded relation (or prewellordering). It can also be used to show that the canonical expansions of universally Baire sets are unique (which we did in Lemma 2.6).
$R^{V[g]}$
is a universally Baire wellfounded relation (or prewellordering). It can also be used to show that the canonical expansions of universally Baire sets are unique (which we did in Lemma 2.6).
The following lemma is the first part of the proof of Theorem 9.1, as outlined above.
Lemma 9.5. Let
![]() $\lambda $
be a limit of
$\lambda $
be a limit of
![]() $\mathord {<}\lambda $
-strong cardinals, and let
$\mathord {<}\lambda $
-strong cardinals, and let
![]() $G \subseteq \mathrm {Col}(\omega ,\mathord {<}\lambda )$
be a V-generic filter. Then in the symmetric extension
$G \subseteq \mathrm {Col}(\omega ,\mathord {<}\lambda )$
be a V-generic filter. Then in the symmetric extension
![]() $V(\mathbb {R}^*_G)$
, every Suslin set that admits a Suslin-norm is co-Suslin.
$V(\mathbb {R}^*_G)$
, every Suslin set that admits a Suslin-norm is co-Suslin.
Proof. Let A be a Suslin set in
![]() $V(\mathbb {R}^*_G)$
that admits a regular Suslin-norm
$V(\mathbb {R}^*_G)$
that admits a regular Suslin-norm
![]() $\varphi $
, and let
$\varphi $
, and let
![]() $R_\le $
and
$R_\le $
and
![]() $R_<$
be the Suslin relations coding
$R_<$
be the Suslin relations coding
![]() $\varphi $
. Let
$\varphi $
. Let
![]() $T, \ T_\le $
, and
$T, \ T_\le $
, and
![]() $T_<$
be trees in
$T_<$
be trees in
![]() $V(\mathbb {R}^{*}_{G})$
projecting to
$V(\mathbb {R}^{*}_{G})$
projecting to
![]() $A, \ R_\le $
and
$A, \ R_\le $
and
![]() $R_<$
respectively. By the usual homogeneity argument
$R_<$
respectively. By the usual homogeneity argument
![]() $T, \ T_\le $
and
$T, \ T_\le $
and
![]() $T_<$
are in
$T_<$
are in
![]() $V[G \mathord {\restriction } \xi ]$
for some
$V[G \mathord {\restriction } \xi ]$
for some
![]() $\xi < \lambda $
. Let
$\xi < \lambda $
. Let
![]() $\kappa < \lambda $
be a
$\kappa < \lambda $
be a
![]() $\mathord {<}\lambda $
-strong cardinal in
$\mathord {<}\lambda $
-strong cardinal in
![]() $V[G \mathord {\restriction } \xi ]$
.
$V[G \mathord {\restriction } \xi ]$
.
In any generic extension of
![]() $V[G \mathord {\restriction } \xi ]$
by a poset of size less than
$V[G \mathord {\restriction } \xi ]$
by a poset of size less than
![]() $\lambda $
, the pair of relations
$\lambda $
, the pair of relations
![]() $(\mathrm {p}[T_\le ], \mathrm {p}[T_<])$
codes a norm on the set
$(\mathrm {p}[T_\le ], \mathrm {p}[T_<])$
codes a norm on the set
![]() $\mathrm {p}[T]$
, since (for instance) the properties of
$\mathrm {p}[T]$
, since (for instance) the properties of
![]() $(A, R_\le , R_<)$
in
$(A, R_\le , R_<)$
in
![]() $V(\mathbb {R}^*_G)$
that ensure coding a norm are preserved under restriction to the reals of a smaller universe.
$V(\mathbb {R}^*_G)$
that ensure coding a norm are preserved under restriction to the reals of a smaller universe.
Let
![]() $\alpha = 2^{2^\kappa }$
. Define the set
$\alpha = 2^{2^\kappa }$
. Define the set
![]() $A_0 = \mathrm {p}[T]^{V[G \mathord {\restriction } \alpha ]}$
and the pair of relations
$A_0 = \mathrm {p}[T]^{V[G \mathord {\restriction } \alpha ]}$
and the pair of relations
![]() $(R^{0}_{\le }, R^{0}_{<}) = (\mathrm {p}[T_\le ], \mathrm {p}[T_<])^{V[G \mathord {\restriction } \alpha ]}$
. Then the pair
$(R^{0}_{\le }, R^{0}_{<}) = (\mathrm {p}[T_\le ], \mathrm {p}[T_<])^{V[G \mathord {\restriction } \alpha ]}$
. Then the pair
![]() $(R^{0}_{\le }, R^{0}_{<})$
codes a norm
$(R^{0}_{\le }, R^{0}_{<})$
codes a norm
![]() $\varphi _0$
on the set
$\varphi _0$
on the set
![]() $A_0$
.
$A_0$
.
Claim 9.6. In
![]() $V[G \mathord {\restriction } \alpha ]$
, the set
$V[G \mathord {\restriction } \alpha ]$
, the set
![]() $A_0$
is
$A_0$
is
![]() $\lambda $
-universally Baire and the norm
$\lambda $
-universally Baire and the norm
![]() $\varphi _0$
on
$\varphi _0$
on
![]() $A_0$
is a
$A_0$
is a
![]() $\mathrm {uB}_{\lambda }$
-norm.
$\mathrm {uB}_{\lambda }$
-norm.
Proof. Fix
![]() $\eta < \lambda $
. We will show that the set
$\eta < \lambda $
. We will show that the set
![]() $A_0$
is
$A_0$
is
![]() $\eta $
-universally Baire and the norm
$\eta $
-universally Baire and the norm
![]() $\varphi _0$
on
$\varphi _0$
on
![]() $A_0$
is a
$A_0$
is a
![]() $\mathrm {uB}_{\eta }$
-norm. By increasing
$\mathrm {uB}_{\eta }$
-norm. By increasing
![]() $\eta $
, we may assume that
$\eta $
, we may assume that
![]() $\alpha < \eta $
and
$\alpha < \eta $
and
![]() $\left |V_\eta \right | = \eta $
. Take an elementary embedding
$\left |V_\eta \right | = \eta $
. Take an elementary embedding
![]() $j \colon V[G \mathord {\restriction } \xi ] \to M$
with critical point
$j \colon V[G \mathord {\restriction } \xi ] \to M$
with critical point
![]() $\kappa $
, where M is transitive,
$\kappa $
, where M is transitive,
![]() $M^\omega \subseteq M, \ V_\eta [G \mathord {\restriction } \xi ] \subseteq M$
and
$M^\omega \subseteq M, \ V_\eta [G \mathord {\restriction } \xi ] \subseteq M$
and
![]() $\eta < j(\kappa )$
.
$\eta < j(\kappa )$
.
Let
![]() $A_\eta = \mathrm {p}[j(T)]^{V[G \mathord {\restriction } \alpha ]}, \ R_{\le }^{\eta } = \mathrm {p}[j(T_\le )]^{V[G \mathord {\restriction } \alpha ]}$
and
$A_\eta = \mathrm {p}[j(T)]^{V[G \mathord {\restriction } \alpha ]}, \ R_{\le }^{\eta } = \mathrm {p}[j(T_\le )]^{V[G \mathord {\restriction } \alpha ]}$
and
![]() $R_{<}^{\eta } = \mathrm {p}[j(T_<)]^{V[G \mathord {\restriction } \alpha ]}$
. Then
$R_{<}^{\eta } = \mathrm {p}[j(T_<)]^{V[G \mathord {\restriction } \alpha ]}$
. Then
![]() $A_\eta , \ R_{\le }^{\eta }$
and
$A_\eta , \ R_{\le }^{\eta }$
and
![]() $R_{<}^{\eta }$
are
$R_{<}^{\eta }$
are
![]() $\eta $
-universally Baire in
$\eta $
-universally Baire in
![]() $V[G \mathord {\restriction } \alpha ]$
by a theorem of Woodin (see Steel [Reference Steel23, Theorem 4.5].)
$V[G \mathord {\restriction } \alpha ]$
by a theorem of Woodin (see Steel [Reference Steel23, Theorem 4.5].)
In any generic extension of M by a poset of size less than
![]() $j(\lambda )$
, the pair of relations
$j(\lambda )$
, the pair of relations
![]() $(\mathrm {p}[j(T_\le )], \mathrm {p}[j(T_<)])$
codes a norm on the set
$(\mathrm {p}[j(T_\le )], \mathrm {p}[j(T_<)])$
codes a norm on the set
![]() $\mathrm {p}[j(T)]$
, by the elementarity of j. Since
$\mathrm {p}[j(T)]$
, by the elementarity of j. Since
![]() $\alpha < j(\lambda )$
and the models
$\alpha < j(\lambda )$
and the models
![]() $M[G \mathord {\restriction } \alpha ]$
and
$M[G \mathord {\restriction } \alpha ]$
and
![]() $V[G \mathord {\restriction } \alpha ]$
have the same reals, it follows that the pair
$V[G \mathord {\restriction } \alpha ]$
have the same reals, it follows that the pair
![]() $(R_{\le }^{\eta }, R_{<}^{\eta })$
codes a regular norm
$(R_{\le }^{\eta }, R_{<}^{\eta })$
codes a regular norm
![]() $\varphi _\eta $
on the set
$\varphi _\eta $
on the set
![]() $A_\eta $
. We have then that
$A_\eta $
. We have then that
![]() $\varphi _\eta $
is a
$\varphi _\eta $
is a
![]() $\mathrm {uB}_{\eta }$
-norm on
$\mathrm {uB}_{\eta }$
-norm on
![]() $A_\eta $
in
$A_\eta $
in
![]() $V[G \mathord {\restriction } \alpha ]$
.
$V[G \mathord {\restriction } \alpha ]$
.
Using j to map branches of trees pointwise, we get
![]() $A_0 \subseteq A_\eta , \ R_{\le }^{0} \subseteq R_{\le }^{\eta }$
, and
$A_0 \subseteq A_\eta , \ R_{\le }^{0} \subseteq R_{\le }^{\eta }$
, and
![]() $R_{<}^{0} \subseteq R_{<}^{\eta }$
. By Lemma 9.3, these inclusions imply that the set
$R_{<}^{0} \subseteq R_{<}^{\eta }$
. By Lemma 9.3, these inclusions imply that the set
![]() $A_0$
is an initial segment of the set
$A_0$
is an initial segment of the set
![]() $A_\eta $
under its norm
$A_\eta $
under its norm
![]() $\varphi _\eta $
, and that the norm
$\varphi _\eta $
, and that the norm
![]() $\varphi _0$
on
$\varphi _0$
on
![]() $A_0$
is the restriction of
$A_0$
is the restriction of
![]() $\varphi _\eta $
to this initial segment. By Remark 9.4, in
$\varphi _\eta $
to this initial segment. By Remark 9.4, in
![]() $V[G \mathord {\restriction } \alpha ]$
, the set
$V[G \mathord {\restriction } \alpha ]$
, the set
![]() $A_0$
is
$A_0$
is
![]() $\eta $
-universally Baire and the norm
$\eta $
-universally Baire and the norm
![]() $\varphi _0$
on
$\varphi _0$
on
![]() $A_0$
is a
$A_0$
is a
![]() $\mathrm {uB}_{\eta }$
-norm.
$\mathrm {uB}_{\eta }$
-norm.
Now we complete the proof of Lemma 9.5. By the claim, we may fix
![]() $\lambda $
-absolutely complementing pairs of trees
$\lambda $
-absolutely complementing pairs of trees
![]() $(T^*,\tilde {T}), \ (T_\le ^*, \tilde {T}_\le )$
, and
$(T^*,\tilde {T}), \ (T_\le ^*, \tilde {T}_\le )$
, and
![]() $(T_<^*,\tilde {T}_<)$
in
$(T_<^*,\tilde {T}_<)$
in
![]() $V[G \mathord {\restriction } \alpha ]$
for
$V[G \mathord {\restriction } \alpha ]$
for
![]() $A_0, \ R_{\le }^{0}$
, and
$A_0, \ R_{\le }^{0}$
, and
![]() $R_{<}^{0}$
, respectively, and define the canonical expansions
$R_{<}^{0}$
, respectively, and define the canonical expansions
![]() $A^* = \mathrm {p}[T^*]^{V(\mathbb {R}^*_G)}, \ R_\le ^* = \mathrm {p}[T_\le ^*]^{V(\mathbb {R}^*_G)}$
and
$A^* = \mathrm {p}[T^*]^{V(\mathbb {R}^*_G)}, \ R_\le ^* = \mathrm {p}[T_\le ^*]^{V(\mathbb {R}^*_G)}$
and
![]() $R_<^* = \mathrm {p}[T_<^*]^{V(\mathbb {R}^*_G)}$
.
$R_<^* = \mathrm {p}[T_<^*]^{V(\mathbb {R}^*_G)}$
.
Because the pair of relations
![]() $(R_{\le }^{0}, R_{<}^{0})$
codes a norm on the set
$(R_{\le }^{0}, R_{<}^{0})$
codes a norm on the set
![]() $A_0$
, it follows that the pair of relations
$A_0$
, it follows that the pair of relations
![]() $(R_\le ^*, R_<^*)$
codes a regular norm
$(R_\le ^*, R_<^*)$
codes a regular norm
![]() $\varphi ^*$
on the set
$\varphi ^*$
on the set
![]() $A^*$
by generic absoluteness for
$A^*$
by generic absoluteness for
![]() $\Sigma ^1_1(\mathrm {p}[T^*], \mathrm {p}[\tilde {T}], \mathrm {p}[T_\le ^*], \mathrm {p}[\tilde {T}_\le ], \mathrm {p}[T_<^*], \mathrm {p}[\tilde {T}_<])$
.
$\Sigma ^1_1(\mathrm {p}[T^*], \mathrm {p}[\tilde {T}], \mathrm {p}[T_\le ^*], \mathrm {p}[\tilde {T}_\le ], \mathrm {p}[T_<^*], \mathrm {p}[\tilde {T}_<])$
.
We have
![]() $A \subseteq A^*$
by Lemma 2.5, which can be seen as an instance of
$A \subseteq A^*$
by Lemma 2.5, which can be seen as an instance of
![]() $\Sigma ^1_1(\mathrm {p}[T], \mathrm {p}[\tilde {T}])$
generic absoluteness. Similarly,
$\Sigma ^1_1(\mathrm {p}[T], \mathrm {p}[\tilde {T}])$
generic absoluteness. Similarly,
![]() $R_\le \subseteq R_\le ^*$
and
$R_\le \subseteq R_\le ^*$
and
![]() $R_< \subseteq R_<^*$
. By Lemma 9.3 again, these inclusions imply that the set A is an initial segment of the set
$R_< \subseteq R_<^*$
. By Lemma 9.3 again, these inclusions imply that the set A is an initial segment of the set
![]() $A^*$
under the norm
$A^*$
under the norm
![]() $\varphi ^*$
. In
$\varphi ^*$
. In
![]() $V(\mathbb {R}^*_G)$
, the norm
$V(\mathbb {R}^*_G)$
, the norm
![]() $\varphi ^*$
is an
$\varphi ^*$
is an
![]() $\mathrm {ScS}$
-norm where
$\mathrm {ScS}$
-norm where
![]() $\mathrm {ScS}$
denotes the pointclass of Suslin co-Suslin sets, so its inital segment A is a Suslin co-Suslin set as in Remark 9.4, as desired.
$\mathrm {ScS}$
denotes the pointclass of Suslin co-Suslin sets, so its inital segment A is a Suslin co-Suslin set as in Remark 9.4, as desired.
Remark 9.7. In [Reference Schindler and Yasuda21], a pointclass
![]() $\Gamma $
consisting of universally Baire sets of reals is defined to be productive if it is closed under complements and projections, and satisfies that statement that, for all
$\Gamma $
consisting of universally Baire sets of reals is defined to be productive if it is closed under complements and projections, and satisfies that statement that, for all
![]() $A \subseteq \omega ^{\omega } \times \omega ^{\omega }$
in (or continuously reducible to a member of)
$A \subseteq \omega ^{\omega } \times \omega ^{\omega }$
in (or continuously reducible to a member of)
![]() $\Gamma $
, in all set-generic forcing extensions
$\Gamma $
, in all set-generic forcing extensions
![]() $V[H]$
, the sets
$V[H]$
, the sets
![]() $\{ y : \exists x \in \omega ^{\omega } (x,y) \in A^{V[H]} \}$
and
$\{ y : \exists x \in \omega ^{\omega } (x,y) \in A^{V[H]} \}$
and
![]() $(\{y \in \omega ^{\omega } : \exists x \in \omega ^{\omega } (x,y) \in A\})^{V[H]}$
are equivalent. An argument very similar to the proof of Lemma 9.5 shows that the collection of universally Baire sets of reals is productive in
$(\{y \in \omega ^{\omega } : \exists x \in \omega ^{\omega } (x,y) \in A\})^{V[H]}$
are equivalent. An argument very similar to the proof of Lemma 9.5 shows that the collection of universally Baire sets of reals is productive in
![]() $V(\mathbb {R}^{*}_{G})$
, assuming the hypotheses of the lemma. We conjecture that this fact (and in fact a stronger fact) already follows from just the theory
$V(\mathbb {R}^{*}_{G})$
, assuming the hypotheses of the lemma. We conjecture that this fact (and in fact a stronger fact) already follows from just the theory
![]() $\mathsf {AD}^{+}$
+ ‘All sets of reals are universally Baire’.
$\mathsf {AD}^{+}$
+ ‘All sets of reals are universally Baire’.
More specifically, we conjecture that if V is a model of
![]() $\mathsf {AD}^+$
+ ‘All sets of reals are universally Baire’, then for every set of reals A, in all set generic extensions
$\mathsf {AD}^+$
+ ‘All sets of reals are universally Baire’, then for every set of reals A, in all set generic extensions
![]() $V[G*H]$
, there is an elementary embedding
$V[G*H]$
, there is an elementary embedding
with
![]() $j(A^{V[G]})=A^{V[G*H]}$
.
$j(A^{V[G]})=A^{V[G*H]}$
.
Before proceeding with the proof of Theorem 9.1, we make a remark about the necessity of assuming in Lemma 9.5 that the Suslin set of reals A admits a Suslin-norm.
Remark 9.8. If
![]() $\lambda $
is a Woodin cardinal, then Lemma 9.5 holds even without the hypothesis that the set has a Suslin-norm: every Suslin set in
$\lambda $
is a Woodin cardinal, then Lemma 9.5 holds even without the hypothesis that the set has a Suslin-norm: every Suslin set in
![]() $V(\mathbb {R}^*_G)$
is co-Suslin by a theorem of Woodin (see Larson [Reference Larson10, Theorem 1.5.12] or Steel [Reference Steel23, Theorem 4.4]). However, in our application, we do not want to make the assumption that
$V(\mathbb {R}^*_G)$
is co-Suslin by a theorem of Woodin (see Larson [Reference Larson10, Theorem 1.5.12] or Steel [Reference Steel23, Theorem 4.4]). However, in our application, we do not want to make the assumption that
![]() $\lambda $
is a Woodin cardinal; together with the assumption that it is a limit of Woodin cardinals, this would be significantly stronger than the hypothesis of the main theorem.
$\lambda $
is a Woodin cardinal; together with the assumption that it is a limit of Woodin cardinals, this would be significantly stronger than the hypothesis of the main theorem.
However, if
![]() $\lambda $
is singular, then the hypothesis of the existence of a Suslin-norm in Lemma 9.5 is necessary: in
$\lambda $
is singular, then the hypothesis of the existence of a Suslin-norm in Lemma 9.5 is necessary: in
![]() $V(\mathbb {R}^*_G)$
, there is a Suslin set of reals that is not co-Suslin. An example was pointed out to us by Woodin (in an email on November 26, 2014). We generalize this example to show that if
$V(\mathbb {R}^*_G)$
, there is a Suslin set of reals that is not co-Suslin. An example was pointed out to us by Woodin (in an email on November 26, 2014). We generalize this example to show that if
![]() $\mathsf {ZF}$
holds and
$\mathsf {ZF}$
holds and
![]() $\omega _1$
is singular (as in the symmetric model obtained by the Levy collapse at a singular cardinal), then there is a Suslin set of reals that is not co-Suslin.
$\omega _1$
is singular (as in the symmetric model obtained by the Levy collapse at a singular cardinal), then there is a Suslin set of reals that is not co-Suslin.
Take a sequence of countable ordinals
![]() $\langle \alpha _n : n < \omega \rangle $
that is cofinal in
$\langle \alpha _n : n < \omega \rangle $
that is cofinal in
![]() $\omega _1$
, and let A be the set of all reals of the form
$\omega _1$
, and let A be the set of all reals of the form
![]() $n^\frown x$
, where
$n^\frown x$
, where
![]() $n < \omega $
and x is a real coding a wellordering of
$n < \omega $
and x is a real coding a wellordering of
![]() $\omega $
of order type at most
$\omega $
of order type at most
![]() $\alpha _n$
. This set A is Suslin, as witnessed by the tree of attempts to build a real
$\alpha _n$
. This set A is Suslin, as witnessed by the tree of attempts to build a real
![]() $n^\frown x$
and a function
$n^\frown x$
and a function
![]() $f : \omega \to \alpha _n$
such that x codes a linear ordering on
$f : \omega \to \alpha _n$
such that x codes a linear ordering on
![]() $\omega $
and f is strictly increasing with respect to this linear ordering.
$\omega $
and f is strictly increasing with respect to this linear ordering.
Assume toward a contradiction that the set A is co-Suslin. The set of all reals
![]() $n^\frown x$
where
$n^\frown x$
where
![]() $n < \omega $
and x is a real coding any wellordering of
$n < \omega $
and x is a real coding any wellordering of
![]() $\omega $
is also Suslin, so the intersection of this set with the complement of A is Suslin.
$\omega $
is also Suslin, so the intersection of this set with the complement of A is Suslin.
In other words, the set of all reals
![]() $n^\frown x$
where
$n^\frown x$
where
![]() $n < \omega $
and x is a real coding a wellordering of
$n < \omega $
and x is a real coding a wellordering of
![]() $\omega $
of order type greater than
$\omega $
of order type greater than
![]() $\alpha _n$
is Suslin. Then by considering leftmost branches we can choose, for each
$\alpha _n$
is Suslin. Then by considering leftmost branches we can choose, for each
![]() $n < \omega $
, a real
$n < \omega $
, a real
![]() $x_n$
coding a wellordering of
$x_n$
coding a wellordering of
![]() $\omega $
of order type greater than
$\omega $
of order type greater than
![]() $\alpha _n$
. This is a contradiction because it allows us to define a wellordering of
$\alpha _n$
. This is a contradiction because it allows us to define a wellordering of
![]() $\omega $
of order type
$\omega $
of order type
![]() $\omega _1$
.
$\omega _1$
.
Proof of Theorem 9.1.
Working in the derived model
![]() $D(V,\lambda ,G)$
, suppose toward a contradiction that not every set of reals is Suslin. Since
$D(V,\lambda ,G)$
, suppose toward a contradiction that not every set of reals is Suslin. Since
![]() $\mathsf {AD}^+$
holds, the set of Suslin cardinals is closed in
$\mathsf {AD}^+$
holds, the set of Suslin cardinals is closed in
![]() $\Theta $
(see Ketchersid [Reference Ketchersid, Babinkostova, Caicedo, Geschke and Scheepers9] or Larson [Reference Larson11] for a proof) so there is a largest Suslin cardinal
$\Theta $
(see Ketchersid [Reference Ketchersid, Babinkostova, Caicedo, Geschke and Scheepers9] or Larson [Reference Larson11] for a proof) so there is a largest Suslin cardinal
![]() $\kappa $
(by Corollary 6.19 of [Reference Larson11]). The pointclass of
$\kappa $
(by Corollary 6.19 of [Reference Larson11]). The pointclass of
![]() $\kappa $
-Suslin sets (equivalently, of all Suslin sets) is non-selfdual, and it has the prewellordering property, meaning that every Suslin set has a Suslin-norm (see Jackson [Reference Jackson, Foreman and Kanamori3, Lemma 3.6] and Remark 6.6 of [Reference Larson11]). So we can fix a complete Suslin set A of
$\kappa $
-Suslin sets (equivalently, of all Suslin sets) is non-selfdual, and it has the prewellordering property, meaning that every Suslin set has a Suslin-norm (see Jackson [Reference Jackson, Foreman and Kanamori3, Lemma 3.6] and Remark 6.6 of [Reference Larson11]). So we can fix a complete Suslin set A of
![]() $D(V,\lambda ,G)$
and note that a Suslin-norm on A exists.
$D(V,\lambda ,G)$
and note that a Suslin-norm on A exists.
By Lemma 9.5, the set A is Suslin and co-Suslin in
![]() $V(\mathbb {R}^*_G)$
, which means that A is in
$V(\mathbb {R}^*_G)$
, which means that A is in
![]() $\mathrm {Hom}^*_G$
. We can fix then a
$\mathrm {Hom}^*_G$
. We can fix then a
![]() $\xi < \lambda $
and
$\xi < \lambda $
and
![]() $\lambda $
-absolutely complementing trees
$\lambda $
-absolutely complementing trees
![]() $T_{A}$
and
$T_{A}$
and
![]() $\tilde {T}_{A}$
on
$\tilde {T}_{A}$
on
![]() $\omega \times \mathrm {Ord}$
in
$\omega \times \mathrm {Ord}$
in
![]() $V[G \mathord {\restriction } \xi ]$
such that
$V[G \mathord {\restriction } \xi ]$
such that
![]() $A = \mathrm {p}[T_{A}]^{V(\mathbb {R}^{*}_{G})}$
. Letting
$A = \mathrm {p}[T_{A}]^{V(\mathbb {R}^{*}_{G})}$
. Letting
![]() $A_{0} = \mathrm {p}[T_{A}]^{V[G \mathord {\restriction } \xi ]}$
, we have then that
$A_{0} = \mathrm {p}[T_{A}]^{V[G \mathord {\restriction } \xi ]}$
, we have then that
![]() $A = A_0^{V(\mathbb {R}^*_G)}$
. This means that
$A = A_0^{V(\mathbb {R}^*_G)}$
. This means that
![]() $V[G\mathord {\restriction } \xi ] \models \omega ^\omega \setminus A_0 \in \mathrm {uB}_{\lambda }$
as well, so the set
$V[G\mathord {\restriction } \xi ] \models \omega ^\omega \setminus A_0 \in \mathrm {uB}_{\lambda }$
as well, so the set
![]() $\omega ^\omega \setminus A_0$
has a
$\omega ^\omega \setminus A_0$
has a
![]() $\mathrm {uB}_{\lambda }$
-semiscale
$\mathrm {uB}_{\lambda }$
-semiscale
![]() $\vec {\varphi }$
in
$\vec {\varphi }$
in
![]() $V[G \mathord {\restriction } \xi ]$
by Steel [Reference Steel23, Theorem 5.3]. (This result uses the fact that
$V[G \mathord {\restriction } \xi ]$
by Steel [Reference Steel23, Theorem 5.3]. (This result uses the fact that
![]() $\mathrm {uB}_{\lambda } = \mathrm {Hom}_{\mathord {<}\lambda }$
because
$\mathrm {uB}_{\lambda } = \mathrm {Hom}_{\mathord {<}\lambda }$
because
![]() $\lambda $
is a limit of Woodin cardinals. Also, the semiscale obtained by Steel is a scale, but we do not need the additional lower semicontinuity property of scales here.)
$\lambda $
is a limit of Woodin cardinals. Also, the semiscale obtained by Steel is a scale, but we do not need the additional lower semicontinuity property of scales here.)
As in Section 3, to say that
![]() $\vec {\varphi }$
is a
$\vec {\varphi }$
is a
![]() $\mathrm {uB}_{\lambda }$
-semiscale means that its component norms
$\mathrm {uB}_{\lambda }$
-semiscale means that its component norms
![]() $\varphi _n$
are
$\varphi _n$
are
![]() $\mathrm {uB}_{\lambda }$
-norms, uniformly in n. (In fact, the uniformity is automatic here because the pointclass
$\mathrm {uB}_{\lambda }$
-norms, uniformly in n. (In fact, the uniformity is automatic here because the pointclass
![]() $\mathrm {uB}_{\lambda }$
is closed under countable unions.) More precisely, the relation
$\mathrm {uB}_{\lambda }$
is closed under countable unions.) More precisely, the relation
![]() $R_0$
coding the semiscale
$R_0$
coding the semiscale
![]() $\vec {\varphi }$
, defined by
$\vec {\varphi }$
, defined by
is
![]() $\lambda $
-universally Baire, where
$\lambda $
-universally Baire, where
![]() $\bar {n}$
indicates the constant function from
$\bar {n}$
indicates the constant function from
![]() $\omega $
to n. Fix trees
$\omega $
to n. Fix trees
![]() $T_{R}$
and
$T_{R}$
and
![]() $\tilde {T}_{R}$
in
$\tilde {T}_{R}$
in
![]() $V[G \mathord {\restriction } \xi ]$
witnessing this, and let R denote the expanded relation
$V[G \mathord {\restriction } \xi ]$
witnessing this, and let R denote the expanded relation
![]() $R_{0}^{V(\mathbb {R}^{*}_{G})}$
.
$R_{0}^{V(\mathbb {R}^{*}_{G})}$
.
The expanded relation R codes a semiscale on the set
![]() $\omega ^\omega \setminus A$
, which was our universal co-Suslin set of the derived model. One way to see this is to use the fact that
$\omega ^\omega \setminus A$
, which was our universal co-Suslin set of the derived model. One way to see this is to use the fact that
![]() $(\mathrm {HC}^{V[G \mathord {\restriction } \xi ]}; \mathord {\in }, A_0,R_0) \prec (\mathrm {HC}^*_G; \mathord {\in }, A, R)$
because
$(\mathrm {HC}^{V[G \mathord {\restriction } \xi ]}; \mathord {\in }, A_0,R_0) \prec (\mathrm {HC}^*_G; \mathord {\in }, A, R)$
because
![]() $\lambda $
is a limit of Woodin cardinals (see Steel [Reference Steel23, Lemma 7.3].) Another way is to apply
$\lambda $
is a limit of Woodin cardinals (see Steel [Reference Steel23, Lemma 7.3].) Another way is to apply
![]() $\mathrm {pos}\Sigma ^1_1(\mathrm {p}[T_A],\mathrm {p}[\tilde {T}_A],\mathrm {p}[T_R],\mathrm {p}[\tilde {T}_R])$
generic absoluteness.
$\mathrm {pos}\Sigma ^1_1(\mathrm {p}[T_A],\mathrm {p}[\tilde {T}_A],\mathrm {p}[T_R],\mathrm {p}[\tilde {T}_R])$
generic absoluteness.
Because the relation R is in
![]() $\mathrm {Hom}^*_G$
, it is in the derived model
$\mathrm {Hom}^*_G$
, it is in the derived model
![]() $D(V,\lambda ,G)$
. In
$D(V,\lambda ,G)$
. In
![]() $D(V,\lambda ,G)$
, the tree of the semiscale coded by R witnesses that the set
$D(V,\lambda ,G)$
, the tree of the semiscale coded by R witnesses that the set
![]() $\omega ^\omega \setminus A$
is Suslin (i.e., that the set A is co-Suslin), giving a contradiction.
$\omega ^\omega \setminus A$
is Suslin (i.e., that the set A is co-Suslin), giving a contradiction.
Finally, we establish the last remaining component required for the proof of the main theorem:
Lemma 9.9. Let
![]() $\lambda $
be a limit of Woodin cardinals and a limit of strong cardinals, and let
$\lambda $
be a limit of Woodin cardinals and a limit of strong cardinals, and let
![]() $G \subseteq \mathrm {Col}(\omega ,\mathord {<}\lambda )$
be a V-generic filter. Then every set of reals in
$G \subseteq \mathrm {Col}(\omega ,\mathord {<}\lambda )$
be a V-generic filter. Then every set of reals in
![]() $\mathrm {Hom}^*_G$
is universally Baire in
$\mathrm {Hom}^*_G$
is universally Baire in
![]() $L^F(\mathbb {R}^*_G, \mathrm {Hom}^*_G)^{V(\mathbb {R}^*_G)}$
.
$L^F(\mathbb {R}^*_G, \mathrm {Hom}^*_G)^{V(\mathbb {R}^*_G)}$
.
Proof. Let
![]() $A\in \mathrm {Hom}^*_G$
, which means that
$A\in \mathrm {Hom}^*_G$
, which means that
![]() $\omega ^\omega \setminus A \in \mathrm {Hom}^*_G$
as well. As in the proof of Theorem 9.1, it follows from Steel [Reference Steel23, Theorem 5.3] (using the fact that
$\omega ^\omega \setminus A \in \mathrm {Hom}^*_G$
as well. As in the proof of Theorem 9.1, it follows from Steel [Reference Steel23, Theorem 5.3] (using the fact that
![]() $\lambda $
is a limit of Woodin cardinals) that A and its complement admit
$\lambda $
is a limit of Woodin cardinals) that A and its complement admit
![]() $\mathrm {Hom}^*_G$
-semiscales. By Lemma 5.7 and the discussion preceding it, the fact that
$\mathrm {Hom}^*_G$
-semiscales. By Lemma 5.7 and the discussion preceding it, the fact that
![]() $\lambda $
is a limit of strong cardinals implies that every set in
$\lambda $
is a limit of strong cardinals implies that every set in
![]() $\mathrm {Hom}^*_G$
is universally Baire in
$\mathrm {Hom}^*_G$
is universally Baire in
![]() $V(\mathbb {R}^*_G)$
. So in
$V(\mathbb {R}^*_G)$
. So in
![]() $V(\mathbb {R}^*_G)$
, the set A is universally Baire and there are
$V(\mathbb {R}^*_G)$
, the set A is universally Baire and there are
![]() $\mathrm {uB}$
-semiscales on A and
$\mathrm {uB}$
-semiscales on A and
![]() $\omega ^\omega \setminus A$
. By Theorem 4.2, then, with
$\omega ^\omega \setminus A$
. By Theorem 4.2, then, with
![]() $\Gamma = \mathrm {Hom}^{*}_{G}, \ A$
is universally Baire in
$\Gamma = \mathrm {Hom}^{*}_{G}, \ A$
is universally Baire in
![]() $L^F(\mathbb {R}^*_G, \mathrm {Hom}^*_G)^{V(\mathbb {R}^*_G)}$
.
$L^F(\mathbb {R}^*_G, \mathrm {Hom}^*_G)^{V(\mathbb {R}^*_G)}$
.
Acknowledgements
The authors thank John Steel for permission to include an adaptation of his unpublished argument for Theorem 9.1 and Hugh Woodin for pointing out the result mentioned in Remark 1.2. This work began at the Mathematisches Forschungsinstitut Oberwolfach, where the second author was a Leibniz Fellow, in the Spring of 2012.
Competing interest
The authors have no competing interests to declare.
Financial support
The research of the first author was partially supported by NSF grants DMS-0801009, DMS-1201494 and DMS-1764320. The second author’s work is funded by the National Science Center, Poland under the Maestro Call, registration number UMO-2023/50/A/ST1/00258. The third author was supported by NSF grant DMS-1044150.