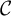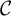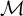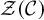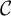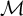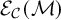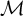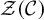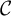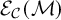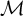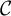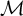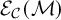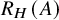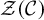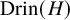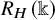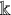Reflective centers of module categories and quantum K-matrices

Abstract

Our work is motivated by obtaining solutions to the quantum reflection equation (qRE) by categorical methods. To start, given a braided monoidal category ${\mathcal {C}}$ and ${\mathcal {C}}$-module category ${\mathcal {M}}$, we introduce a version of the Drinfeld center ${\mathcal {Z}}({\mathcal {C}})$ of ${\mathcal {C}}$ adapted for ${\mathcal {M}}$; we refer to this category as the reflective center ${\mathcal {E}}_{\mathcal {C}}({\mathcal {M}})$ of ${\mathcal {M}}$. Just like ${\mathcal {Z}}({\mathcal {C}})$ is a canonical braided monoidal category attached to ${\mathcal {C}}$, we show that ${\mathcal {E}}_{\mathcal {C}}({\mathcal {M}})$ is a canonical braided module category attached to ${\mathcal {M}}$; its properties are investigated in detail.

Our second goal pertains to when ${\mathcal {C}}$ is the category of modules over a quasitriangular Hopf algebra H, and ${\mathcal {M}}$ is the category of modules over an H-comodule algebra A. We show that the reflective center ${\mathcal {E}}_{\mathcal {C}}({\mathcal {M}})$ here is equivalent to a category of modules over an explicit algebra, denoted by $R_H(A)$, which we call the reflective algebra of A. This result is akin to ${\mathcal {Z}}({\mathcal {C}})$ being represented by the Drinfeld double ${\operatorname {Drin}}(H)$ of H. We also study the properties of reflective algebras.

Our third set of results is also in the Hopf setting above. We show that reflective algebras are quasitriangular H-comodule algebras, and we examine their corresponding quantum K-matrices; this yields solutions to the qRE. We also establish that the reflective algebra $R_H(\mathbb {k})$ is an initial object in the category of quasitriangular H-comodule algebras, where $\mathbb {k}$ is the ground field. The case when H is the Drinfeld double of a finite group is illustrated.

1 Introduction

Quasitriangular Hopf algebras and their (universal) quantum R-matrices, introduced by Drinfeld [Dri87], play a fundamental role in many areas of mathematics and mathematical physics, such as low-dimensional topology, representation theory, quantum field theory and exactly solvable models. More generally, Joyal and Street [JS91] introduced the notion of braided monoidal categories, which, similarly, are central objects for the categorical foundations of numerous studies. There are well known ways to construct both structures:

1. (1) Given a Hopf algebra H, its Drinfeld double ${\operatorname {Drin}}(H)$ is a quasitriangular Hopf algebra with an explicit R-matrix.

2. (2) For a monoidal category ${\mathcal {C}}$ , one constructs its Drinfeld center ${\mathcal {Z}}({\mathcal {C}})$ , which is a braided monoidal category.

The two constructions work in tandem: The Drinfeld center of the module category of a finite-dimensional Hopf algebra H is isomorphic to the module category of its Drinfeld double.

Going a step further, on the categorical side, Brochier [Bro13] introduced the notion of a braided module category over a braided monoidal category. On the Hopf algebra side, Kolb [Kol20] defined the notion of a quasitriangular (left) H-comodule algebra A of a quasitriangular Hopf algebra H; such an algebra is equipped with a (universal) quantum K-matrix $K \in H \otimes A$ . There are broad parallels between universal quantum R-matrices and K-matrices:

1. (a) Universal quantum R-matrices and K-matrices automatically satisfy the quantum Yang–Baxter and reflection equations, respectively.

2. (b) The former give rise to representations of the Artin braid groups of type A, while the latter give rise to representations of the Artin braid groups of type B.

3. (c) The former are used in studying exactly solvable models in statistical mechanics without boundary, while the latter are used for solving models with boundary.

In summary, following Balagovic’s presentation [Bal19] on her joint paper with Kolb [BK19],

The most important class of quasitriangular comodule algebras that was studied to date is the class of quantum symmetric pair coideal subalgebras, introduced in the foundational works of Letzter [Let99, Let02]. These are quantum analogs of the pairs $(U(\mathfrak {k}), U(\mathfrak {g}))$ where $\mathfrak {g}$ is a complex simple Lie algebra (or more generally a symmetrizable Kac–Moody algebra) and $\mathfrak {k}$ is a symmetric Lie subalgebra (the fixed point of an involutive automorphism of $\mathfrak {g}$ ). The quasitriangularity for this class of comodule algebras was established by recursively building a quantum K-matrix using the Lusztig bar involution [BW18a,BK19,BW18b,AV22]. For coideal subalgebras of arbitrary Drinfeld doubles of bosonizations of Yetter–Drinfeld modules of diagonal types, where bar involutions need not exist, quantum K-matrices were constructed from star products on partial bosonizations of Nichols algebras [KY20].

Given the vast applications of quantum K-matrices and braided module categories, one can ask the following two questions:

1. (Q1) Is there a version of the Drinfeld double construction (1) with an input of an H-comodule algebra for a quasitriangular Hopf algebra and an output a quasitriangular H-comodule algebra with an explicit quantum K-matrix?

2. (Q2) Is there a version of the Drinfeld center construction (2) with an input a module category of a braided monoidal category ${\mathcal {C}}$ and an output a braided module category of ${\mathcal {C}}$ ?

The goals of this paper are to fully resolve both questions. This leads to strong methods for the construction of quasitriangular comodule algebras, quantum K-matrices and braided module categories that can be applied in broad generality. The following table summarizes our constructions and notions:

Before stating the precise formulation of our results, we note that all linear structures are over an algebraically closed field $\mathbb {k}$ . For a $\mathbb {k}$ -algebra A, let ${{A}\text {-}\mathsf {mod}}$ denote the category of left A-modules.

To proceed with the aims above, take a braided monoidal category ${\mathcal {C}}$ and a left ${\mathcal {C}}$ -module category ${\mathcal {M}}$ . In Definition 4.1, we define the reflective center of ${\mathcal {M}}$ with respect to ${\mathcal {C}}$ , denoted by ${\mathcal {E}}_{\mathcal {C}}({\mathcal {M}})$ and motivated by the construction of the Drinfeld center ${\mathcal {Z}}({\mathcal {C}})$ of ${\mathcal {C}}$ . The following results are established for ${\mathcal {E}}_{\mathcal {C}}({\mathcal {M}})$ in parallel of the known properties of ${\mathcal {Z}}({\mathcal {C}})$ :

Theorem A (Proposition 4.3, Corollary 4.6).

Retain the notation above. Then the reflective center ${\mathcal {E}}_{\mathcal {C}}({\mathcal {M}})$ has the following properties.

1. (a) ${\mathcal {E}}_{\mathcal {C}}({\mathcal {M}})$ is a braided left ${\mathcal {C}}$ -module category.

2. (b) ${\mathcal {E}}_{\mathcal {C}}({\mathcal {M}})$ is abelian when ${\mathcal {M}}$ is exact, is finite when ${\mathcal {C}}$ is finite and ${\mathcal {M}}$ is exact, and is semisimple when ${\mathcal {C}}$ and ${\mathcal {M}}$ are finite and semisimple.

3. (c) ${\mathcal {E}}_{\mathcal {C}}({\mathcal {M}})$ is also a left ${\mathcal {Z}}({\mathcal {C}})$ -module category.

Now for the rest of the introduction, take ${\mathcal {C}} = {{H}\text {-}\mathsf {mod}}$ and ${\mathcal {M}} = {{A}\text {-}\mathsf {mod}}$ for

• • H a finite-dimensional quasitriangular Hopf algebra over $\mathbb {k}$ ,

• • A a left H-comodule algebra over $\mathbb {k}$ .

Our first main result for this Hopf setting is given below. This is achieved via Theorem A(a) and by applying results in Section 3.6 on transferring a braided module category structure across an equivalence of categories.

Theorem B (Lemma 6.2, Proposition 6.4, Theorem 6.6).

There exists a category of Doi–Hopf modules ${}_A^{\widehat {H}} \mathsf {DH}(H)$ for a certain left H-module coalgebra $\widehat {H}$ defined in Section 5.2, and a certain algebra $R_H(A)$ defined in Section 5.3, such that

(1.1) $$ \begin{align} {\mathcal{E}}_{{{H}\text{-}\mathsf{mod}}}({{A}\text{-}\mathsf{mod}}) \; \cong \; {}_A^{\widehat{H}} \mathsf{DH}(H) \; \cong \; {{R_H(A)}\text{-}\mathsf{mod}} \end{align} $$

as braided left module categories over ${{H}\text {-}\mathsf {mod}}$ . See Figure 1 for the location of these actions.

The H-module coalgebra $\widehat {H}$ is defined in Definition 5.7, and as discussed in Remark 5.8, it is a version of Majid’s transmuted Hopf algebra constructed in [Maj91].

We refer to $R_H(A)$ as the reflective algebra of A with respect to H. It is defined as a crossed product algebra, $A \rtimes _H (\widehat {H}^{*})^{\mathrm {op}}$ , as described at the beginning of Section 5.3.1. It plays an analogous role for reflective centers as the Drinfeld double ${\operatorname {Drin}}(H)$ of H does for the Drinfeld center ${\mathcal {Z}}({{H}\text {-}\mathsf {mod}})$ .

Figure 1 Isomorphic braided module categories over ${{H}\text {-}\mathsf {mod}}$ .

We obtain the following consequence of Theorem B.

Corollary C (Corollary 6.9).

The reflective algebra $R_H(A)$ is a quasitriangular left H-comodule algebra, with an explicit quantum K-matrix given in terms of a dual basis of H.

The reflective algebra $R_H(\mathbb {k})$ for the canonical left H-comodule algebra $\mathbb {k}$ is of particular interest due to the following result.

Theorem D (Theorem 6.15).

The reflective algebra $R_H(\mathbb {k})$ and its quantum K-matrix from Corollary C is an initial object in the category of quasitriangular left H-comodule algebras.

The results above are illustrated in Section 6.4 in the case when H is the Drinfeld double of a finite group, ${\operatorname {Drin}}(G)$ , and for the left ${\operatorname {Drin}}(G)$ -comodule algebra $\mathbb {k}$ .

Finally, using Theorem A(c) and the braided isomorphism between ${\mathcal {Z}}({{H}\text {-}\mathsf {mod}})$ and ${{{\operatorname {Drin}}(H)}\text {-}\mathsf {mod}}$ , we get a module category action of ${{{\operatorname {Drin}}(H)}\text {-}\mathsf {mod}}$ on ${{R_H(A)}\text {-}\mathsf {mod}}$ . This yields the result below.

Proposition E (Proposition 6.20).

The reflective algebra $R_H(A)$ is a left ${\operatorname {Drin}}(H)$ -comodule algebra, with an explicit comodule structure given in terms of the quantum R-matrix of H.

2 Preliminaries on (braided) monoidal categories

In this section, we review terminology pertaining to braided monoidal categories. We refer the reader to [EGNO15] and [TV17] for general information. We first review background material on monoidal categories in Section 2.1. Then in Section 2.2, we recall braided monoidal categories, the Drinfeld center construction of a braided category from a monoidal category and the connection to quantum R-matrices in Hopf case. We assume that all categories here are locally small (i.e., the collection of morphisms between any two objects is a set).

2.1 Monoidal categories

We refer the reader to [EGNO15,TV17,Wal24] for further details.

Monoidal categories. A monoidal category consists of a category ${\mathcal {C}}$ equipped with a bifunctor $\otimes \colon {\mathcal {C}} \times {\mathcal {C}} \to {\mathcal {C}}$ , a natural isomorphism $a_{X,Y,Z}\colon (X \otimes Y) \otimes Z \overset {\sim }{\to } X \otimes (Y \otimes Z)$ for $X,Y,Z \in {\mathcal {C}}$ , an object , and natural isomorphisms and for $X \in {\mathcal {C}}$ , satisfying pentagon and triangle axioms.

A (strong) monoidal functor between monoidal categories and is a functor $F\colon {\mathcal {C}} \to {\mathcal {C}}'$ equipped with a natural isomorphism $F_{X,Y}\colon F(X) \otimes ' F(Y) \ {\stackrel {\sim }{\to }} \ F(X \otimes Y)$ for $X,Y \in {\mathcal {C}}$ , and an isomorphism in ${\mathcal {C}}'$ , satisfying associativity and unitality constraints.

An equivalence (resp., isomorphism) of monoidal categories is provided by a monoidal functor between the two monoidal categories that yields an equivalence (resp., isomorphism) of the underlying categories; it is denoted by $\overset {\otimes }{\simeq }$ (resp., $\overset {\otimes }{\cong }$ ).

Opposite monoidal category. Given a monoidal category , its opposite monoidal category is defined as , with $X \otimes ^{\mathrm {op}} Y := Y \otimes X$ and $a^{\mathrm {op}} _{X,Y,Z} := a^{-1}_{Z,Y,X}$ and $l_X^{\mathrm {op}} = r_X$ and $r_X^{\mathrm {op}} = l_X$ , for all $X,Y,Z \in {\mathcal {C}}$ .

Rigidity. A monoidal category is rigid if it comes equipped with left and right dual objects; that is, for each $X \in {\mathcal {C}}$ , there exist, respectively, an object $X^{*} \in {\mathcal {C}}$ with co/evaluation maps and , and an object ${}^{*}X \in {\mathcal {C}}$ with co/evaluation maps , , satisfying coherence conditions of left and right duals.

Linearity over $\mathbb {k}$ , finiteness. We now discuss certain $\mathbb {k}$ -linear monoidal categories. A $\mathbb {k}$ -linear abelian category ${\mathcal {C}}$ is locally finite if, for any two objects $V,W$ in ${\mathcal {C}}$ , $\operatorname {Hom}_{{\mathcal {C}}}(V,W)$ is a finite-dimensional $\mathbb {k}$ -vector space and every object has finite length. A locally finite category ${\mathcal {C}}$ is finite if there are enough projectives and finitely many isomorphism classes of simple objects. Equivalently, a $\mathbb {k}$ -linear category ${\mathcal {C}}$ is finite if it is equivalent to the category of finite-dimensional modules over a finite-dimensional $\mathbb {k}$ -algebra.

Tensor and fusion categories. A tensor category is an abelian, $\mathbb {k}$ -linear, locally finite, rigid, monoidal category such that $\otimes $ is $\mathbb {k}$ -linear in each slot and . A tensor functor is a $\mathbb {k}$ -linear, exact, faithful, monoidal functor F between tensor categories ${\mathcal {C}}$ and ${\mathcal {C}}'$ , with . A tensor category is said to be a fusion category if it is both finite and semisimple. If ${\mathcal {C}}$ is a tensor (resp., finite tensor, fusion) category, then so is ${\mathcal {C}}^{\otimes \mathrm {op}}$ .

Deligne tensor product. Let ${\mathcal {C}}$ and ${\mathcal {C}}'$ be two tensor categories. Then the Deligne tensor product of ${\mathcal {C}}$ and ${\mathcal {C}}'$ is a $\mathbb {k}$ -linear, abelian category ${\mathcal {C}} \boxtimes {\mathcal {C}}'$ endowed with a functor $\boxtimes : {\mathcal {C}} \times {\mathcal {C}}' \to {\mathcal {C}} \boxtimes {\mathcal {C}}'$ that is $\mathbb {k}$ -linear and right exact in each variable, and is universal among such functors out of ${\mathcal {C}} \times {\mathcal {C}}$ . We also have that ${\mathcal {C}} \boxtimes {\mathcal {C}}'$ is a monoidal category where $(X \boxtimes X') \otimes ^{{\mathcal {C}} \boxtimes {\mathcal {C}}'} (Y \boxtimes Y') := (X \otimes ^{{\mathcal {C}}} Y) \boxtimes (X' \otimes ^{{\mathcal {C}}'} Y')$ , for $X, Y \in {\mathcal {C}}$ , $X', Y' \in {\mathcal {C}}'$ , and . Moreover, the Deligne tensor product of two tensor (resp., finite tensor, fusion) categories is a tensor (resp., finite tensor, fusion) category.

Hopf case. The category H- $\mathsf {fdmod}$ of finite-dimensional $\mathbb {k}$ -modules over a (finite-dimensional) Hopf algebra H is a (finite) tensor category. If, further, H is a semisimple Hopf algebra, then H- $\mathsf {fdmod}$ is a fusion category. If H and $H'$ are Hopf algebras over $\mathbb {k}$ , then $(H\text {-}\mathsf {mod})^{\otimes \mathrm {op}} \overset {\otimes }{\simeq } H^{\mathrm {cop}}\text {-}\mathsf {mod}$ , for the co-opposite Hopf algebra $H^{\mathrm {cop}}$ . We also have that $H\text {-}\mathsf {mod} \boxtimes H'\text {-}\mathsf {mod} \overset {\otimes }{\simeq } (H \otimes _{\mathbb {k}} H')\text {-}\mathsf {mod}$ for the standard tensor product of Hopf algebras $H \otimes _{\mathbb {k}} H'$ over $\mathbb {k}$ .

2.2 Braided categories, Drinfeld centers and quantum R-matrices

See [EGNO15, Sections 8.1, 8.3, 8.5, 8.6], [Maj00, Sections 2.1, 7.1], [HS20, Section 4.1], [Kas95] for further details.

Braided categories. A monoidal category is braided if it is a equipped with a natural isomorphism $c_{X,Y}\colon X \otimes Y \overset {\sim }{\to } Y \otimes X$ for $X,Y \in {\mathcal {C}}$ (braiding), such that the following hexagon axioms hold for each $X,Y,Z \in {\mathcal {C}}$ :

(2.1) $$ \begin{align} c_{X \otimes Y, Z} &= a_{Z,X,Y} \circ (c_{X,Z} \otimes \mathsf{Id}_Y) \circ a_{X,Z,Y}^{-1} \circ (\mathsf{Id}_X \otimes c_{Y,Z}) \circ a_{X,Y,Z}, \end{align} $$

(2.2) $$ \begin{align} c_{X, Y \otimes Z} &=a_{Y,Z,X}^{-1} \circ (\mathsf{Id}_Y \otimes c_{X,Z}) \circ a_{Y,X,Z} \circ (c_{X,Y} \otimes \mathsf{Id}_Z) \circ a_{X,Y,Z}^{-1}. \end{align} $$

We also have a mirror braiding on ${\mathcal {C}}$ given by $c_{Y,X}^{-1}\colon X \otimes Y \overset {\sim }{\to } Y \otimes X$ for $X,Y \in {\mathcal {C}}$ . We refer to the braided monoidal category as the mirror of .

A braided monoidal functor between braided monoidal categories ${\mathcal {C}}$ and ${\mathcal {C}}'$ is a monoidal functor $(F, F_{-,-},F_0)\colon {\mathcal {C}} \to {\mathcal {C}}'$ such that

(2.3) $$ \begin{align} F_{Y,X} \circ c^{\prime}_{F(X),F(Y)} = F(c_{X,Y}) \circ F_{X,Y} \end{align} $$

for all $X,Y \in {\mathcal {C}}$ . An equivalence (resp., isomorphism) of braided monoidal categories is a braided monoidal functor that yields an equivalence (resp., isomorphism) of the underlying categories. Similar notions exist for tensor categories and tensor functors.

Drinfeld centers. An important example of a braided monoidal category is the Drinfeld center ${\mathcal {Z}}({\mathcal {C}})$ of a monoidal category . Its objects are pairs $(V, c^V)$ , where V is an object of ${\mathcal {C}}$ and

$$ \begin{align*}c^V:=\{c^V_X \colon X \otimes V \overset{\sim}{\to} V \otimes X\}_{X \in {\mathcal{C}}}\end{align*} $$

is a natural isomorphism, called a half-braiding, satisfying

(2.4) $$ \begin{align} c^V_{X \otimes Y} = \; a_{V,X,Y} \circ (c^V_X \otimes \mathsf{Id}_{Y}) \circ a^{-1}_{X,V,Y} \circ (\mathsf{Id}_{X} \otimes c^V_Y) \circ a_{X,Y,V}. \end{align} $$

Morphisms $(V, c^V) \to (W, c^W)$ of ${\mathcal {Z}}({\mathcal {C}})$ are given by $f \in \operatorname {Hom}_{{\mathcal {C}}}(V,W)$ such that, for all $X \in {\mathcal {C}}$ ,

$$\begin{align*}(f \otimes \mathsf{Id}_X) \circ c^V_X = c^W_X \circ (\mathsf{Id}_X \otimes f). \end{align*}$$

The monoidal product of ${\mathcal {Z}}({\mathcal {C}})$ is $(V,c^V) \otimes (W,c^W):=(V\otimes W, c^{V \otimes W})$ , for all $X \in {\mathcal {C}}$ :

(2.5) $$ \begin{align} c^{V\otimes W}_X \; := \; a_{V,W,X}^{-1} \circ (\mathsf{Id}_V \otimes c^W_X) \circ a_{V,X,W} \circ (c^V_X \otimes \mathsf{Id}_W) \circ a^{-1}_{X,V,W}. \end{align} $$

An important feature of ${\mathcal {Z}}({\mathcal {C}})$ is the braiding defined by

Moreover, if ${\mathcal {C}}$ is a (finite) tensor category, then ${\mathcal {Z}}({\mathcal {C}})$ is a braided (finite) tensor category.

Drinfeld centers in Hopf case and Yetter–Drinfeld modules. Take a finite-dimensional Hopf algebra $H:=(H,m,u,\Delta ,\varepsilon ,S)$ over $\mathbb {k}$ , where $\Delta (h) =: h_{(1)} \otimes _{\mathbb {k}} h_{(2)}$ (sumless Sweedler notation). When ${\mathcal {C}} = H$ - $\mathsf {mod}$ , we have the isomorphisms of braided monoidal categories below,

(2.6) $$ \begin{align} {\mathcal{Z}}(H\text{-}\mathsf{mod}) \;\; \overset{\otimes}{\cong} \;\; {{\vphantom{\mathsf{YD}}}^{H}_{H}{\mathsf{YD}}} \;\; \overset{\otimes}{\cong} \; \;{\operatorname{Drin}}(H)\text{-}\mathsf{mod}, \end{align} $$

where ${{\vphantom {\mathsf {YD}}}^{{H}}_{{H}}{\mathsf {YD}}}$ is the category of left Yetter–Drinfeld modules over H, and ${\operatorname {Drin}}(H)$ is the Drinfeld double of H. We provide the details below.

The objects of the category of left Yetter–Drinfeld modules ${{\vphantom {\mathsf {YD}}}^{H}_{H}{\mathsf {YD}}}$ are triples , where is a left H-module and $(V, \partial ^V)$ is a left H-comodule with $\partial ^V(v):= v_{\langle -1 \rangle } \otimes _{\mathbb {k}} v_{\langle 0 \rangle } \in H \otimes _{\mathbb {k}} V$ , subject to the following compatibility condition between and $\partial ^V$ :

A morphism of ${{\vphantom {\mathsf {YD}}}^{H}_{H}{\mathsf {YD}}}$ is a linear map which is simultaneously a left H-module morphism and a left H-comodule morphism. Then the first isomorphism of (2.6) holds via the assignments

(2.7)

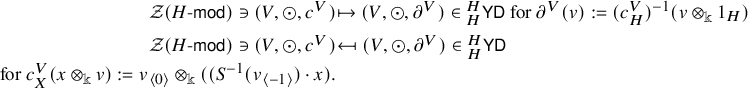
Here, H in $c^V_H$ is the regular left H-module, and $(X,\cdot )$ is an arbitrary left H-module.

However, the Drinfeld double of H is a Hopf algebra ${\operatorname {Drin}}(H)$ , which is, as a start, equal to $H^{*} \otimes _{\mathbb {k}} H$ as a vector space. Next, denote the standard left and right actions of H on $H^{*}$ by $\twoheadrightarrow $ and $\twoheadleftarrow $ , respectively. That is, $h \twoheadrightarrow \xi := \langle \xi _{(2)}, h \rangle \xi _{(1)}$ with $\langle h \twoheadrightarrow \xi , h' \rangle = \langle \xi , h'h \rangle $ , and $\xi \twoheadleftarrow h := \langle \xi _{(1)}, h \rangle \xi _{(2)}$ with $\langle \xi \twoheadleftarrow h, h' \rangle = \langle \xi , h h' \rangle $ , with $h, h' \in H$ and $\xi \in H^{*}$ . Here, we use the Hopf pairing between $H^{*}$ and H. Then ${\operatorname {Drin}}(H)$ contains H and $(H^{*})^{\mathrm {op}}$ as Hopf subalgebras, and the product of ${\operatorname {Drin}}(H)$ between elements of H and $(H^{*})^{\mathrm {op}}$ is given by

(2.8) $$ \begin{align} h \xi \; =\; (h_{(3)} \twoheadrightarrow \xi \twoheadleftarrow S(h_{(1)})) h_{(2)} = \langle \xi_{(1)}, S(h_{(1)}) \rangle \; \langle \xi_{(3)}, h_{(3)} \rangle\; \xi_{(2)} h_{(2)} \end{align} $$

for $h \in H, \; \xi \in (H^{*})^{\mathrm {op}}$ . Moreover, ${\operatorname {Drin}}(H)$ has the tensor product unit, coproduct and counit. Then the second isomorphism of (2.6) holds via the assignments

(2.9)

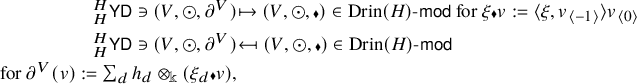
with $\{h_d, \xi _d\}_d$ a dual basis of H. (The latter assignment is independent of choice of dual basis of H.)

Quasitriangular Hopf algebras, quantum R -matrices. Again, take a Hopf algebra ${H:=(H,m,u,\Delta ,\varepsilon ,S)}$ over $\mathbb {k}$ , where $\Delta (h) =: h_{(1)} \otimes _{\mathbb {k}} h_{(2)}$ (sumless Sweedler notation). Moreover, denote $\otimes := \otimes _{\mathbb {k}}$ . We say that H is quasitriangular if there exists an invertible element

(2.10) $$ \begin{align} R = \textstyle \sum_i s_i \otimes t_i \in H \otimes H \;\; (\textit{quantum}\ R\textit{-matrix}), \end{align} $$

with inverse, $R^{-1}:= \textstyle \sum _i s^i \otimes t^i \; \in H \otimes H$ , such that

(2.11) $$ \begin{align} \textstyle \sum_i (s_i)_{(1)} \otimes (s_i)_{(2)} \otimes t_i \; &= \textstyle\; \sum_{j,k} s_j \otimes s_k \otimes t_j t_k, \end{align} $$

(2.12) $$ \begin{align} \kern-1pt\textstyle\sum_i s_i \otimes (t_i)_{(1)} \otimes (t_i)_{(2)} \; &= \textstyle\; \sum_{j,k} s_j s_k \otimes t_k \otimes t_j, \end{align} $$

(2.13) $$ \begin{align} \quad\ \textstyle \sum_i s_i h_{(1)} \otimes t_i h_{(2)} \; &= \textstyle\; \sum_i h_{(2)} s_i \otimes h_{(1)} t_i. \end{align} $$

Alternatively, we will also use the following notation for quantum R-matrices. Take

$$\begin{align*}R_{ab}:= \textstyle \sum_i s_i \; (\text{in the }a\text{-th slot})\; \otimes \; t_i \; (\text{in the }b\text{-th slot}) \otimes \; 1_H \; \text{(in other slots)} \end{align*}$$

(e.g., $R_{13} = \sum _i s_i \otimes 1_H \otimes t_i$ ). Then, the conditions (2.11)–(2.13) are written, respectively, as follows:

$$\begin{align*}(\Delta \otimes \mathsf{Id}_H) (R) = R_{13} R_{23}, \quad \quad (\mathsf{Id}_H \otimes \Delta) (R) = R_{13} R_{12}, \quad \quad R \Delta(h) = \Delta^{\mathrm{op}}(h) R \quad \forall h \in H. \end{align*}$$

For a quasitriangular Hopf algebra $(H,R)$ , we also have the identities below:

(2.14) $$ \begin{align} &(\varepsilon \otimes \mathsf{Id})(R) = 1_H, \hspace{.28in} (\mathsf{Id} \otimes \varepsilon)(R) = 1_H,\qquad\quad\ \,\qquad\qquad \end{align} $$

(2.15) $$ \begin{align} &R^{-1} = (S \otimes \mathsf{Id})(R), \quad R = (\mathsf{Id} \otimes S)(R^{-1}), \quad R = (S \otimes S)(R), \end{align} $$

where $\mathbb {k} \otimes H$ and $H \otimes \mathbb {k}$ are identified with H.

For example, for a finite-dimensional Hopf algebra H with dual bases $\{h_d, \xi _d\}_d$ , we have that the Drinfeld double ${\operatorname {Drin}}(H)$ of H is quasitriangular, with R-matrix

$$ \begin{align*} R_{{\operatorname{Drin}}(H)} := \textstyle \sum_d 1_{H^{*}} \otimes h_d \otimes \xi_d \otimes 1_H \; \in {\operatorname{Drin}}(H) \otimes {\operatorname{Drin}}(H). \end{align*} $$

Moreover, quantum R-matrices of H are tied to braidings of ${{H}\text {-}\mathsf {mod}}$ as we see below.

Lemma 2.16. The tensor category ${{H}\text {-}\mathsf {mod}}$ is braided with

$$\begin{align*}c_{X,Y} : X \otimes Y \to Y \otimes X, \quad x \otimes y \mapsto \textstyle \sum_i (t_i \cdot y) \otimes (s_i \cdot x), \end{align*}$$

for $R:= \sum _i s_i \otimes t_i \in H \otimes H$ , if and only if R is a quantum R-matrix for H.

3 Preliminaries and results on (braided) module categories

Throughout this section, let be a monoidal category, unless stated otherwise. We review module categories over ${\mathcal {C}}$ and module functors between them in Section 3.1. The collection of module functors form a category, which we discuss in Section 3.2. Exact module categories are reviewed in Section 3.3. Then, bimodule categories and their centers are discussed in Section 3.4. Finally, braided module categories are introduced in Section 3.5, braided module functors are studied in Section 3.6, and connections to quantum K-matrices are presented in Section 3.7.

3.1 Module categories

See [EGNO15, Sections 7.1–7.3]] for details. A left ${\mathcal {C}}$ -module category is a category ${\mathcal {M}}$ equipped with an action bifunctor $\triangleright : {\mathcal {C}} \times {\mathcal {M}} \to {\mathcal {M}}$ , a natural isomorphism $m_{X,Y,M}\colon (X \otimes Y) \triangleright M \overset {\sim }{\to } X \triangleright (Y \triangleright M)$ for $X,Y \in {\mathcal {C}}$ , $M \in {\mathcal {M}}$ , and a natural isomorphism for $M \in {\mathcal {M}}$ , such that the following pentagon and triangle axioms hold for each $X,Y,Z \in {\mathcal {C}}$ and $M \in {\mathcal {M}}$ :

(3.1) $$ \begin{align} m_{X,Y,Z \triangleright M} \circ m_{X \otimes Y, Z,M} &= (\mathsf{Id}_X \triangleright m_{Y,Z,M})\circ m_{X, Y \otimes Z, M}\circ (a_{X,Y,Z} \triangleright \mathsf{Id}_M), \end{align} $$

(3.2)

We sometimes write ${\mathcal {M}}$ or $({\mathcal {M}}, \triangleright )$ to denote $({\mathcal {M}}, \triangleright , m, \lambda )$ for brevity.

A ${\mathcal {C}}$ -module functor between left ${\mathcal {C}}$ -module categories $({\mathcal {M}}, \triangleright , m, \lambda )$ and $({\mathcal {M}}', \triangleright ', m', \lambda ')$ is a functor $F: {\mathcal {M}} \to {\mathcal {M}}'$ equipped with a natural isomorphism,

$$ \begin{align*}s:=\{s_{X,M}: F(X \triangleright M) \ {\stackrel{\sim}{\to}} \ X \triangleright' F(M)\}_{X \in {\mathcal{C}}, M \in {\mathcal{M}}},\end{align*} $$

such that the following coherence axioms hold for each $X,Y \in {\mathcal {C}}$ and $M \in {\mathcal {M}}$ :

(3.3) $$ \begin{align} m^{\prime}_{X,Y,F(M)} \circ s_{X \otimes Y, M} &= (\mathsf{Id}_X \triangleright' s_{Y,M})\circ s_{X, Y \triangleright M}\circ F(m_{X,Y,M}), \end{align} $$

(3.4)

Similarly, a right ${\mathcal {C}}$ -module category is a category ${\mathcal {M}}$ equipped with a bifunctor $\triangleleft \colon {\mathcal {M}} \times {\mathcal {C}} \to {\mathcal {M}}$ , a natural isomorphism $n_{M,X,Y}\colon M \triangleleft (X \otimes Y) \overset {\sim }{\to } (M \triangleleft X) \triangleleft Y$ for $X,Y \in {\mathcal {C}}$ , $M \in {\mathcal {M}}$ , and a natural isomorphism for $M \in {\mathcal {M}}$ , satisfying pentagon and triangle axioms.

A ${\mathcal {C}}$ -module functor between right ${\mathcal {C}}$ -module categories $({\mathcal {M}}, \triangleleft , n, \rho )$ and $({\mathcal {M}}', \triangleleft ', n', \rho ')$ is a functor $F: {\mathcal {M}} \to {\mathcal {M}}'$ equipped with a natural isomorphism,

$$ \begin{align*}t:=\{t_{M,X}: F(M \triangleleft X) \ {\stackrel{\sim}{\to}} \ F(M) \triangleleft' X\}_{X \in {\mathcal{C}}, M \in {\mathcal{M}}},\end{align*} $$

satisfying coherence axioms.

A left module category over a tensor category ${\mathcal {C}}$ is a left ${\mathcal {C}}$ -module category $({\mathcal {M}}, \triangleright )$ that is abelian, $\mathbb {k}$ -linear, locally finite, bilinear on morphisms, such that $- \triangleright M: {\mathcal {C}} \to {\mathcal {M}}$ is exact for all $M \in {\mathcal {M}}$ . A similar notion holds for right module categories. We also assume that module functors between such module categories are additive in each slot.

3.2 Categories of module functors

The collection of ${\mathcal {C}}$ -module functors between left ${\mathcal {C}}$ -module categories ${\mathcal {M}}$ and ${\mathcal {M}}'$ forms a category, which we denote by $\mathsf {Fun}_{{\mathcal {C}}}({\mathcal {M}},{\mathcal {M}}')$ . A morphism in $\mathsf {Fun}_{{\mathcal {C}}}({\mathcal {M}},{\mathcal {M}}')$ from $(F_1, s_1)$ to $(F_2,s_2)$ is a natural transformation from $F_1$ to $F_2$ that is compatible with $s_1$ and $s_2$ . See [EGNO15, Section 7.2] for more information.

The category $\mathsf {Fun}_{{\mathcal {C}}}({\mathcal {M}},{\mathcal {M}}')$ is not always well behaved, but we have the following useful result.

Proposition 3.5 [ENO05, Theorem 2.16].

If ${\mathcal {C}}$ is a fusion category, and ${\mathcal {M}}$ and ${\mathcal {M}}'$ are finite and semisimple left ${\mathcal {C}}$ -module categories, then $\mathsf {Fun}_{{\mathcal {C}}}({\mathcal {M}}, {\mathcal {M}}')$ is a semisimple category.

A subcollection of $\mathsf {Fun}_{{\mathcal {C}}}({\mathcal {M}},{\mathcal {M}}')$ that is better behaved is the collection of right exact ${\mathcal {C}}$ -module functors between left ${\mathcal {C}}$ -module categories ${\mathcal {M}}$ and ${\mathcal {M}}'$ ; their full subcategory of $\mathsf {Fun}_{{\mathcal {C}}}({\mathcal {M}},{\mathcal {M}}')$ is denoted by $\mathsf {Rex}_{{\mathcal {C}}}({\mathcal {M}},{\mathcal {M}}')$ . We also denote the full subcategory of exact ${\mathcal {C}}$ -module functors from ${\mathcal {M}}$ to ${\mathcal {M}}'$ by $\mathsf {Ex}_{{\mathcal {C}}}({\mathcal {M}},{\mathcal {M}}')$ .

3.3 Exact module categories

Assume here that ${\mathcal {C}}$ is a finite tensor category. Here, we recall background material on exact module categories from [EGNO15, Sections 7.5, 7.11].

A locally finite module category $({\mathcal {M}}, \triangleright )$ over ${\mathcal {C}}$ is called exact if for any projective object $P \in {\mathcal {C}}$ and any object $M \in {\mathcal {M}}$ , we have that the object $P \triangleright M$ is projective in ${\mathcal {M}}$ .

Example 3.6. If ${\mathcal {C}}$ is a finite tensor category, then ${\mathcal {C}}$ is an exact left module category over both ${\mathcal {C}}$ and ${\mathcal {C}} \boxtimes {\mathcal {C}}^{\otimes \mathrm {op}}$ ; see [EO04, Example 3.3(i)].

As mentioned above, the category of right exact module category functors is better behaved than the category of ordinary module category functors. To see this, consider the result below.

Proposition 3.7 [EGNO15, Proposition 3.11].

If ${\mathcal {M}}$ and ${\mathcal {M}}'$ are exact, finite, left ${\mathcal {C}}$ -module categories, then $\mathsf {Rex}_{{\mathcal {C}}}({\mathcal {M}}, {\mathcal {M}}')$ is abelian and finite.

We also have that any module category functor from an exact module category is (right) exact.

Proposition 3.8 [EO04].

Let ${\mathcal {M}}$ be an exact, finite left ${\mathcal {C}}$ -module category. Then $\mathsf {Fun}_{{\mathcal {C}}}({\mathcal {M}}, {\mathcal {M}}') = \mathsf {Ex}_{{\mathcal {C}}}({\mathcal {M}}, {\mathcal {M}}')$ for any left ${\mathcal {C}}$ -module category ${\mathcal {M}}'$ .

3.4 Bimodule categories and their centers

Here, we recall material from work of Greenough, [Gre10, Sections 2 and 7]. A ${\mathcal {C}}$ -bimodule category is a tuple $({\mathcal {M}},\triangleright , \triangleleft , m,n,\lambda ,\rho )$ such that $({\mathcal {M}},\triangleright , m,\lambda )$ is a left ${\mathcal {C}}$ -module category and $({\mathcal {M}}, \triangleleft , n,\rho )$ is a right ${\mathcal {C}}$ -module category, with a natural isomorphism, $b:=\{b_{X,M,Y}\colon (X\triangleright M)\triangleleft Y \ {\stackrel {\sim }{\to }} \ X\triangleright (M\triangleleft Y)\}_{X,Y\in {\mathcal {C}}, M\in {\mathcal {M}}},$ satisfying compatibility conditions.

Remark 3.9. Note that $({\mathcal {M}},\triangleright , \triangleleft , m,n,\lambda ,\rho )$ is a ${\mathcal {C}}$ -bimodule category if and only if $({\mathcal {M}},\bar {\triangleright }, \bar {m}, \bar {\lambda })$ a left module category over ${\mathcal {C}} \boxtimes {\mathcal {C}}^{\otimes \mathrm {op}}$ . Here, $(X \boxtimes X') \bar {\triangleright } M \leftrightsquigarrow (X \triangleright M) \triangleleft X'$ , for $X,X' \in {\mathcal {C}}$ and $M \in {\mathcal {M}}$ , and we have similar correspondences between the associativity and unitality constraints.

A functor of ${\mathcal {C}}$ -bimodule categories $F\colon {\mathcal {M}}\to {\mathcal {M}}'$ is at the same time a functor for the left and right ${\mathcal {C}}$ -module structures, with natural isomorphisms for $X\in {\mathcal {C}}$ and $M\in {\mathcal {M}}$ ,

$$ \begin{align*}s_{X,M}\colon F(X\triangleright M)\ {\stackrel{\sim}{\to}} \ X\triangleright' F(M), \qquad t_{M,X}\colon F(M\triangleleft X)\ {\stackrel{\sim}{\to}} \ F(M)\triangleleft' X,\end{align*} $$

satisfying the compatibility condition below for all $X,Y\in {\mathcal {C}}$ , $M\in {\mathcal {M}}$ :

$$ \begin{align*} (\mathsf{Id}_X\triangleright' t_{M,Y}) \circ s_{X,M\triangleleft Y} \circ F(b_{X,M,Y}) = b^{\prime}_{X,F(M),Y} \circ (s_{X,M}\triangleleft' \mathsf{Id}_Y) \circ t_{X\triangleright M,Y}. \end{align*} $$

Given a ${\mathcal {C}}$ -module category, one defines its center by analogy with the center of a monoidal category (cf. Section 2.2).

Definition 3.10. Given a ${\mathcal {C}}$ -bimodule category ${\mathcal {M}}$ , we define its center ${\mathcal {Z}}_{{\mathcal {C}}}({\mathcal {M}})$ as the category consisting of objects $(M,d^M)$ , where M is an object of ${\mathcal {M}}$ and d is a natural isomorphism,

$$ \begin{align*}d^M=\left\{d^M_X\colon X\triangleright M\ {\stackrel{\sim}{\to}} \ M\triangleleft X\right\}_{X\in {\mathcal{C}}} \; \; (\textit{half-braiding}), \end{align*} $$

which satisfies the coherence condition below for all $X,Y \in {\mathcal {C}}$ and $M \in {\mathcal {M}}$ :

(3.11) $$ \begin{align} d_{X\otimes Y}^M = n_{M,X,Y}^{-1} \circ (d_{X}^{M}\triangleleft\mathsf{Id}_Y) \circ b^{-1}_{X,M,Y} \circ (\mathsf{Id}_X\triangleright d_{Y}^{M}) \circ m_{X,Y,M}. \end{align} $$

Morphisms $f\colon (M,d^M)\to (N,d^N)$ are given by morphisms $f\colon M\to N$ in ${\mathcal {M}}$ which commute with the respective half-braidings – that is, for $X \in {\mathcal {C}}$ : $ (f\triangleleft \mathsf {Id}_X) \circ d^M_X = d^N_X \circ (\mathsf {Id}_X\triangleright f). $

Example 3.12. The Drinfeld center ${\mathcal {Z}}({\mathcal {C}})$ of ${\mathcal {C}}$ appears as the special case ${\mathcal {Z}}_{\mathcal {C}}({\mathcal {C}})$ , where ${\mathcal {C}}$ is a ${\mathcal {C}}$ -bimodule via the regular action $X\triangleright V=X\otimes V$ and $V\triangleleft X = V \otimes X$ , along with ${\mathcal {C}}$ -bimodule constraints derived from the monoidal constraints of ${\mathcal {C}}$ as follows: $m_{X,Y,V} = a_{X,Y,V}$ , $n_{V,X,Y} = a^{-1}_{V,X,Y}$ , $\lambda _X = l_X$ , $\rho _X = r_X$ , and $b_{X,V,Y} = a_{X,V,Y}$ for all $X,Y,V \in {\mathcal {C}}$ . In this case, $d_X^V = c_X^V$ for all $X,V \in {\mathcal {C}}$ .

3.5 Braided module categories

Now assume that ${\mathcal {C}}:=({\mathcal {C}},c)$ is braided. We say that a left ${\mathcal {C}}$ -module category $({\mathcal {M}}, \triangleright , m, \lambda )$ is braided if it is equipped with a natural isomorphism,

$$ \begin{align*}e:=\{e_{X,M}\colon X \triangleright M \overset{\sim}{\to} X \triangleright M\}_{X \in {\mathcal{C}}, M \in {\mathcal{M}}} \; \; (\textit{braiding}),\end{align*} $$

such that the following axioms hold for each $X,Y \in {\mathcal {C}}$ and $M \in {\mathcal {M}}$ :

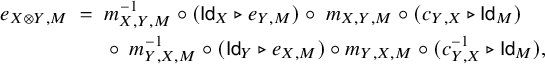(3.13) $$ \begin{align} \begin{aligned} e_{X \otimes Y, M} \; =\; \; & m_{X,Y,M}^{-1} \circ (\mathsf{Id}_X \triangleright e_{Y,M}) \circ\; m_{X,Y,M} \circ (c_{Y,X} \triangleright \mathsf{Id}_M) \\ &\circ \; m_{Y,X,M}^{-1} \circ (\mathsf{Id}_Y \triangleright e_{X,M}) \circ m_{Y,X,M}\circ (c_{Y,X}^{-1} \triangleright \mathsf{Id}_M), \end{aligned} \end{align} $$

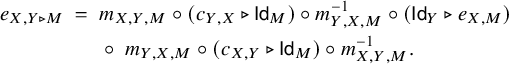(3.14) $$ \begin{align}\begin{aligned} e_{X,Y \triangleright M} \; =\; \; & m_{X,Y,M} \circ (c_{Y,X} \triangleright \mathsf{Id}_M) \circ m_{Y,X,M}^{-1} \circ (\mathsf{Id}_Y \triangleright e_{X,M})\qquad \\ &\circ\; m_{Y,X,M} \circ (c_{X,Y} \triangleright \mathsf{Id}_M) \circ m_{X,Y,M}^{-1}. \qquad\end{aligned}\end{align} $$

Remark 3.15. Let us compare the definition above to the definition of a braided module category in other parts of the literature.

1. (a) In [Kol20, Section 2], the author uses right ${\mathcal {C}}$ -module categories and works in the strict case, and our axiom (3.14) is the braided module category axiom [Kol20, (2.3)]. Moreover, our axiom (3.13) is the equivalent to the axiom [Kol20, (2.3)] via a similar argument to [Kol20, Remarks 2.2 and 2.4] when ${\mathcal {C}}$ is ribbon. More precisely, if ${\mathcal {C}}$ is a ribbon category with a twist transformation $\{\theta _X : X \overset {\sim }{\to } X\}_{X \in {\mathcal {C}}}$ (see [EGNO15, Definition 8.10.1]), then the natural isomorphism e satisfies conditions (3.13)–(3.14) if and only if the natural isomorphism

   $$\begin{align*}\widetilde{e}:=\{\widetilde{e}_{X,M}= e_{X,M} (\theta_X \triangleright \mathsf{Id}_M): X \triangleright M \overset{\sim}{\to} X \triangleright M\}_{X \in {\mathcal{C}}, M \in {\mathcal{M}}} \end{align*}$$
   satisfies the left-hand versions of [Kol20, (2.3)–(2.4)]: (3.14) with e replaced by $\widetilde {e}$ , with
   $$ \begin{align*} &\widetilde{e}_{X \otimes Y, M} = \; m_{X,Y,M} \; (c_{Y,X} \triangleright \mathsf{Id}_M) \; m_{Y,X,M}^{-1} \; (\mathsf{Id}_Y \triangleright \widetilde{e}_{X,M}) \\&\quad m_{Y,X,M}\; (c_{X,Y} \triangleright \mathsf{Id}_M) \; m_{X,Y,M}^{-1} \; (\mathsf{Id}_X \triangleright \widetilde{e}_{Y,M}). \end{align*} $$

   We further note that the conventions of [Kol20] are identical to those in [Bro13, Section 5.1].

2. (b) Considering [DN21, Definition 4.1], our axiom (3.14) is the same as their first braided module category axiom. Also, our axiom (3.13) is the equivalent to their second braided module category axiom, by using the first braided module axiom.

The next result shows that braided module categories can be obtained using braided monoidal functors; cf. [DN21, Proposition 4.12].

Proposition 3.16. We have the following statements.

1. (a) Suppose that ${\mathcal {C}}$ and ${\mathcal {C}}'$ are monoidal categories and $(F, F_{-,-},F_0): {\mathcal {C}} \to {\mathcal {C}}'$ is a (strong) monoidal functor. If $({\mathcal {M}}',\triangleright ',m',\lambda ')$ is a left ${\mathcal {C}}'$ -module category, then $({\mathcal {M}}', \triangleright , m, \lambda )$ is a left ${\mathcal {C}}$ -module category with

   $$ \begin{align*}X \triangleright M := F(X) \triangleright' M,\end{align*} $$
   $m_{X,Y,M} := m^{\prime }_{F(X), F(Y), M} (F^{-1}_{X,Y} \triangleright ' \mathsf {Id}_M)$ and $\lambda _M := \lambda ^{\prime }_M (F_0^{-1} \triangleright ' \mathsf {Id}_M)$ , for $X,Y \in {\mathcal {C}}$ , $M \in {\mathcal {M}}'$ .

2. (b) If $({\mathcal {C}},c)$ and $({\mathcal {C}}', c')$ are braided monoidal categories and $(F, F_{-,-},F_0): {\mathcal {C}} \to {\mathcal {C}}'$ is a braided monoidal functor, then the left ${\mathcal {C}}$ -module category ${\mathcal {C}}'$ from part (a) is braided with

   $$ \begin{align*}e_{X,M} := c^{\prime}_{M,F(X)} \circ c^{\prime}_{F(X),M},\end{align*} $$
   for all $X \in {\mathcal {C}}$ and $M \in {\mathcal {C}}'$ .

Proof. (a) See, for example, [Wal24, Example 3.18].

(b) It suffices to establish (3.13) and (3.14) when $e_{X,M} := c^{\prime }_{M,F(X)} \circ c^{\prime }_{F(X),M}$ , for $X \in {\mathcal {C}}$ and $M \in {\mathcal {C}}'$ . The following computation verifies (3.14):

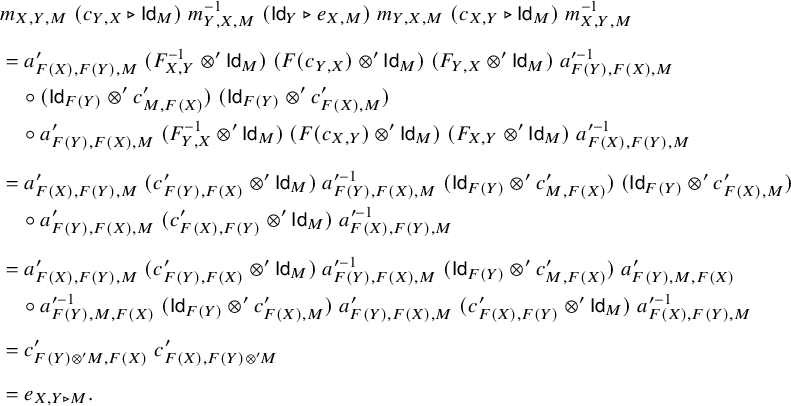$$ \begin{align*} &m_{X,Y,M} \; (c_{Y,X} \triangleright \mathsf{Id}_M) \; m_{Y,X,M}^{-1} \; (\mathsf{Id}_Y \triangleright e_{X,M}) \; m_{Y,X,M} \; (c_{X,Y} \triangleright \mathsf{Id}_M) \; m_{X,Y,M}^{-1} \\[6pt] &= a^{\prime}_{F(X), F(Y), M} \; (F^{-1}_{X,Y} \otimes' \mathsf{Id}_M) \; (F(c_{Y,X}) \otimes' \mathsf{Id}_M) \; (F_{Y,X} \otimes' \mathsf{Id}_M) \; a^{\prime -1}_{F(Y), F(X), M} \\ &\quad \circ (\mathsf{Id}_{F(Y)} \otimes' c^{\prime}_{M,F(X)}) \; (\mathsf{Id}_{F(Y)} \otimes' c^{\prime}_{F(X),M})\\ & \quad \circ a^{\prime}_{F(Y), F(X), M} \; (F^{-1}_{Y,X} \otimes' \mathsf{Id}_M) \; (F(c_{X,Y}) \otimes' \mathsf{Id}_M) \; (F_{X,Y} \otimes' \mathsf{Id}_M) \; a^{\prime -1}_{F(X), F(Y), M} \\[6pt] &= a^{\prime}_{F(X), F(Y), M} \; (c^{\prime}_{F(Y),F(X)} \otimes' \mathsf{Id}_M) \; a^{\prime -1}_{F(Y), F(X), M} \; (\mathsf{Id}_{F(Y)} \otimes' c^{\prime}_{M,F(X)}) \; (\mathsf{Id}_{F(Y)} \otimes' c^{\prime}_{F(X),M})\\ & \quad \circ a^{\prime}_{F(Y), F(X), M} \; (c^{\prime}_{F(X),F(Y)} \otimes' \mathsf{Id}_M) \; a^{\prime -1}_{F(X), F(Y), M} \\[6pt] &= a^{\prime}_{F(X), F(Y), M} \; (c^{\prime}_{F(Y),F(X)} \otimes' \mathsf{Id}_M) \; a^{\prime -1}_{F(Y), F(X), M} \; (\mathsf{Id}_{F(Y)} \otimes' c^{\prime}_{M,F(X)}) \; a^{\prime}_{F(Y),M,F(X)}\\ &\quad \circ a^{\prime -1}_{F(Y),M,F(X)} \; (\mathsf{Id}_{F(Y)} \otimes' c^{\prime}_{F(X),M}) \; a^{\prime}_{F(Y), F(X), M} \; (c^{\prime}_{F(X),F(Y)} \otimes' \mathsf{Id}_M) \; a^{\prime -1}_{F(X), F(Y), M} \\[4pt] & = c^{\prime}_{F(Y)\otimes' M, F(X)} \; c^{\prime}_{F(X), F(Y) \otimes' M} \\[4pt] & = e_{X, Y \triangleright M}. \end{align*} $$

The first and last equations holds by definition; the second equation holds by the braided monoidal functor axiom (2.3); the third equation holds trivially; and the fourth equation holds by the braided monoidal category axioms (2.1) and (2.2).

Likewise, (3.13) holds by applying a combination of the braided monoidal functor axiom (2.3) and the braided monoidal category axioms (2.1) and (2.2).

3.6 Braided module functors

Here, we compare braided module categories via the notions below. For ease, given a left ${\mathcal {C}}$ -module category ${\mathcal {M}}$ with objects $X \in {\mathcal {C}}$ , $M \in {\mathcal {M}}$ , and morphisms $\psi \in {\mathcal {C}}$ , $\phi \in {\mathcal {M}}$ , we write $X \triangleright \phi $ and $\psi \triangleright \mathsf {Id}_M$ for the morphisms $\mathsf {Id}_X \triangleright \phi $ and $\psi \triangleright M$ in ${\mathcal {M}}$ , respectively.

Definition 3.17. A braided ${\mathcal {C}}$ -module functor between braided left ${\mathcal {C}}$ -module categories $({\mathcal {M}},\triangleright , e)$ and $({\mathcal {M}}',\triangleright ', e')$ is a left ${\mathcal {C}}$ -module functor $(F, s)\colon ({\mathcal {M}}, \triangleright ) \to ({\mathcal {M}}', \triangleright ')$ such that

(3.18) $$ \begin{align} e^{\prime}_{X,F(M)} \circ s_{X,M} = s_{X,M} \circ F(e_{X,M}) \end{align} $$

for all $X \in {\mathcal {C}}$ and $M \in {\mathcal {M}}$ . An equivalence (resp., isomorphism) of braided left ${\mathcal {C}}$ -module categories is given by two braided module functors $F\colon {\mathcal {M}}\to {\mathcal {N}}$ and $G\colon {\mathcal {N}}\to {\mathcal {M}}$ between the two module categories that yields an equivalence (resp., isomorphism) of the underlying categories.

The next result is straightforward; the reader may refer to the arXiv version 1 of this article if they are interested in the proof.

Proposition 3.19. Let $(F,s): ({\mathcal {M}},\triangleright ,e) \to ({\mathcal {M}}',\triangleright ',e')$ be a functor of braided left ${\mathcal {C}}$ -module categories and let $G\colon {\mathcal {M}}'\to {\mathcal {M}}$ be a quasi-inverse of F. Then there exists a natural isomorphism $s'$ making $(G,s')$ a functor of braided left ${\mathcal {C}}$ -module categories.

The consequence below is now straightforward to establish.

Corollary 3.20. Braided (left) ${\mathcal {C}}$ -module equivalence is an equivalence relation for braided (left) ${\mathcal {C}}$ -module categories.

We now discuss how to transfer structure for (braided) module categories, particularly across an equivalence of categories. The proof is available in the arXiv version 1 of this article.

Proposition 3.21. Let $F\colon {\mathcal {M}}\to {\mathcal {M}}'$ be a category equivalence with a quasi-inverse $G\colon {\mathcal {M}}'\to {\mathcal {M}}$ .

1. (a) If $({\mathcal {M}}, \triangleright )$ is a left ${\mathcal {C}}$ -module category, then we can define a left ${\mathcal {C}}$ -module category structure $\triangleright '$ on ${\mathcal {M}}'$ via

   $$ \begin{align*}X\triangleright' N \; := \; F(X\triangleright G(N)),\end{align*} $$
   for each $X \in {\mathcal {C}}$ and $N \in {\mathcal {M}}'$ , such that both F and G are left ${\mathcal {C}}$ -module functors.

2. (b) A braiding e on the left ${\mathcal {C}}$ -module category ${\mathcal {M}}$ induces a braiding $e'$ on ${\mathcal {M}}'$ via

   $$ \begin{align*}e^{\prime}_{X,N} \; := \; F(e_{X,G(N)})\colon \; X\triangleright'N\ {\stackrel{\sim}{\to}} \ X\triangleright'N,\end{align*} $$
   for each $X \in {\mathcal {C}}$ and $N \in {\mathcal {M}}'$ , with the left ${\mathcal {C}}$ -module category structure from part (a) such that $F,G$ preserve the braiding.

3.7 Quasitriangular comodule algebras and quantum K-matrices

Assume that H is a quasitriangular Hopf algebra with a quantum R-matrix $R := \sum _i s_i \otimes t_i \in H \otimes H$ . Here, $\otimes := \otimes _{\mathbb {k}}$ . Let A be a left H-comodule algebra with coaction

$$\begin{align*}\delta : A \to H \otimes A, \quad a \mapsto a_{[-1]} \otimes a_{[0]}. \end{align*}$$

Definition 3.22. We say that A is a quasitriangular left H-comodule algebra if it is equipped with an invertible element,

$$\begin{align*}K:= \textstyle \sum_i g_i \otimes p_i \; \in H \otimes A \; \qquad \; (\textit{quantum}\ K\textit{-matrix}), \end{align*}$$

with inverse, $K^{-1}:= \textstyle \sum _i g^i \otimes p^i \; \in H \otimes A$ , such that

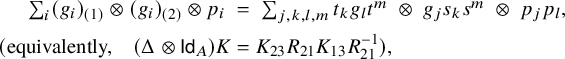(3.23) $$ \begin{align} \begin{aligned} \textstyle \sum_i (g_i)_{(1)} \otimes (g_i)_{(2)}\otimes p_i \;&= \; \textstyle \sum_{j,k,l,m} t_k g_l t^m \; \otimes \; g_j s_k s^m \; \otimes \;p_j p_l, \\[.1pc] (\text{equivalently,} \quad (\Delta \otimes \mathsf{Id}_A) K &= K_{23}R_{21} K_{13} R_{21}^{-1}), \end{aligned} \end{align} $$

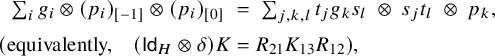(3.24) $$ \begin{align} \begin{aligned} \textstyle \sum_i g_i \otimes (p_i)_{[-1]}\otimes (p_i)_{[0]} \;&= \; \textstyle \sum_{j,k,l} t_j g_k s_l \; \otimes \; s_j t_l \; \otimes \;p_k, \\[.1pc] (\text{equivalently,} \quad (\mathsf{Id}_H \otimes \delta) K &= R_{21} K_{13} R_{12}), \end{aligned} \end{align} $$

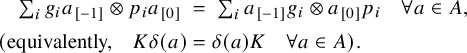(3.25) $$ \begin{align} \begin{aligned} \textstyle \sum_i g_i a_{[-1]} \otimes p_i a_{[0]} \;&= \; \textstyle \sum_i a_{[-1]} g_i \otimes a_{[0]} p_i \quad \forall a \in A, \\[.1pc] (\text{equivalently,} \quad K \delta(a) &= \delta(a) K \quad \forall a \in A). \end{aligned} \end{align} $$

Here, $K_{ab}:= \textstyle \sum _i g_i \; (\text {in the } a\text {-th slot})\; \otimes \; p_i \; (\text {in the } b\text {-th slot}) \otimes \; 1_H \; \text {(in other slots)}.$

Returning to braided module categories, consider the result below.

Lemma 3.26. Retain the notation above for the quasitriangular Hopf algebra $(H,R)$ and the left H-comodule algebra A. Then, the following statements hold.

1. (a) We have that $A\text {-}\mathsf {mod}$ is a left module category over ${{H}\text {-}\mathsf {mod}}$ via

   $$\begin{align*}\triangleright: {{H}\text{-}\mathsf{mod}} \times A\text{-}\mathsf{mod} \to A\text{-}\mathsf{mod}, \quad \left((X, \cdot), (M, \ast)\right) \mapsto (X \otimes M,\; \widetilde{\ast}), \end{align*}$$
   where $a \; \widetilde {\ast } \; (x \otimes m) := (a_{[-1]} \cdot x) \otimes (a_{[0]} \ast m)$ for $a \in A$ , $x \in X$ , $m \in M$ .

2. (b) Take $K:= \sum _i g_i \otimes p_i \in H \otimes A$ , and for $(X, \cdot ) \in {{H}\text {-}\mathsf {mod}}$ , $(M, \ast ) \in A\text {-}\mathsf {mod}$ , take the morphism

   $$\begin{align*}e_{X,M}: X \otimes M \to X \otimes M, \quad x \otimes m \mapsto \textstyle \sum_i (g_i \cdot x) \otimes (p_i \ast m). \end{align*}$$

   Then, the left $({{H}\text {-}\mathsf {mod}})$ -module category $(A\text {-}\mathsf {mod}, \triangleright )$ is braided with braiding given by $e_{X,M}$ if and only if K is a quantum K-matrix for A.

3. (c) Conversely, any braiding for the $({{H}\text {-}\mathsf {mod}})$ -module category ${{A}\text {-}\mathsf {mod}}$ from part (a) is of the form given in part (b) for some element $K:= \textstyle \sum _i g_i \otimes p_i \in H\otimes A$ .

Proof. Part (a) is straightforward to check, and we leave this to the reader. For part (b), we sketch the forward direction; the reverse direction is proved by reversing the arguments.

To proceed, note that if we write H (resp., A) in the subscript of either the braiding c or e, then this denotes the regular left H-module (resp., regular left A-module). Also, denote the inverse of $e_{X,M}$ by $e_{X,M}^{-1} : X \otimes M \to X \otimes M$ and set

$$\begin{align*}K' := e_{H,A}^{-1} (1_H \otimes 1_A) \in H \otimes A. \end{align*}$$

By the naturality of $e_{X,M}^{-1}$ , we obtain that $e_{X,M}^{-1}(x \otimes m) = K' \ \widetilde {\ast } \; (x \otimes m)$ , for $x \in X$ , $m \in M$ . This implies $K K' = K' K = 1_H \otimes 1_A$ . Therefore, $K \in H \otimes A$ is invertible.

To establish (3.23), we compute

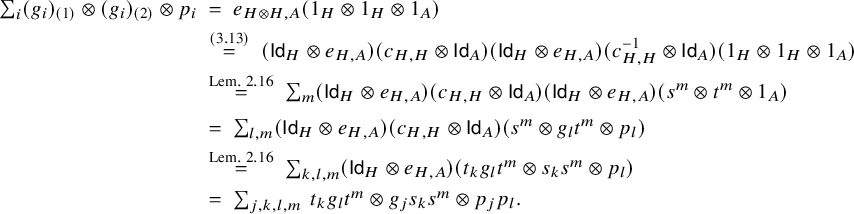$$ \begin{align*} \textstyle \sum_i (g_i)_{(1)} \otimes (g_i)_{(2)} \otimes p_i &\; =\; e_{H \otimes H, A}(1_H \otimes 1_H \otimes 1_A) \\ &\; \overset{\mathrm{(3.13)}}{=}\; (\mathsf{Id}_H \otimes e_{H, A}) (c_{H,H} \otimes \mathsf{Id}_{A}) (\mathsf{Id}_{H} \otimes e_{H, A})(c_{H,H}^{-1} \otimes \mathsf{Id}_{A})(1_H \otimes 1_H \otimes 1_A) \\ &\;\overset{\mathrm{Lem.\;2.16}}{=}\; \textstyle \sum_m (\mathsf{Id}_{H} \otimes e_{H, A}) (c_{H,H} \otimes \mathsf{Id}_{A}) (\mathsf{Id}_{H} \otimes e_{H, A})(s^m \otimes t^m \otimes 1_A) \\[.2pc] &\; =\; \textstyle \sum_{l,m} (\mathsf{Id}_{H} \otimes e_{H, A}) (c_{H,H} \otimes \mathsf{Id}_{A})(s^m \otimes g_l t^m \otimes p_l)\\ &\; \overset{\mathrm{Lem.\;2.16}}{=} \; \textstyle \sum_{k,l,m} (\mathsf{Id}_{H} \otimes e_{H, A}) (t_k g_l t^m \otimes s_k s^m \otimes p_l)\\ &\; =\; \textstyle \sum_{j,k,l,m}\; t_k g_l t^m \otimes g_j s_k s^m \otimes p_j p_l. \end{align*} $$

Likewise to establish (3.24), we compute

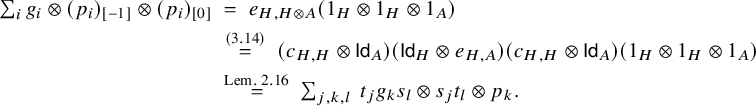$$ \begin{align*} \textstyle \sum_i g_i \otimes (p_i)_{[-1]} \otimes (p_i)_{[0]} &\; =\; e_{H, H \otimes A}(1_H \otimes 1_H \otimes 1_A) \\ &\; \overset{(3.14)}{=}\; (c_{H,H} \otimes \mathsf{Id}_{A})( \mathsf{Id}_{H} \otimes e_{H,A}) (c_{H,H} \otimes \mathsf{Id}_{A}) (1_H \otimes 1_H \otimes 1_A)\\ &\; \overset{\mathrm{Lem.\;2.16}}{=} \; \textstyle \sum_{j,k,l}\; t_j g_k s_l \otimes s_j t_l \otimes p_k. \end{align*} $$

Finally, to show that (3.25) holds, recall that $e_{X,M} : X \otimes M \to X \otimes M$ is an A-module homomorphism. Therefore,

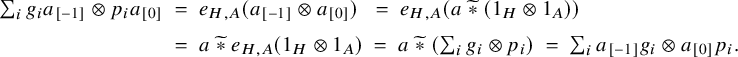$$ \begin{align*} \textstyle \sum_i g_i a_{[-1]} \otimes p_i a_{[0]} & \; = \;e_{H, A}(a_{[-1]} \otimes a_{[0]}) \;\; = \;e_{H, A}(a \; \widetilde{\ast} \; (1_H \otimes 1_A))\\[.2pc] & \;= \;a \; \widetilde{\ast} \; e_{H, A}(1_H \otimes 1_A) \;= \;a \; \widetilde{\ast} \; (\textstyle \sum_i g_i \otimes p_i) \;= \; \textstyle \sum_i a_{[-1]} g_i \otimes a_{[0]} p_i. \end{align*} $$

For part (c), it remains to show that any braiding e on ${{A}\text {-}\mathsf {mod}}$ is given by the action of some element $K\in H\otimes A$ . This follows from a reconstruction argument as in [Maj00, Section 9.4].

Remark 3.27. Let us compare the definition of the quantum K-matrix above with that in [Kol20]. Assume that H is a ribbon Hopf algebra; that is, it is quasitriangular with quantum R-matrix R and contains an invertible central element v such that $\Delta (v) = (v \otimes v) \big ( R_{21}R_{12} \big )^{-1}$ and $v = S(v)$ . Set

$$\begin{align*}\widetilde{K} := K (v^{-1} \otimes 1_A) \in H \otimes A. \end{align*}$$

1. (a) Analogous to Remark 3.15(a), one shows that conditions (3.23)–(3.25) are equivalent to

   (3.28) $$ \begin{align} (\Delta \otimes \mathsf{Id}_A) \widetilde{K} &= \widetilde{K}_{23}R_{21} \widetilde{K}_{13} R_{21},\qquad \end{align} $$
   (3.29) $$ \begin{align} (\mathsf{Id}_H \otimes \delta) \widetilde{K} &= R_{21} \widetilde{K}_{13} R_{21},\quad\,\kern1.7pt\qquad \end{align} $$
   (3.30) $$ \begin{align} \kern2.5pt\quad\widetilde{K} \delta(a) &= \delta(a) \widetilde{K}, \quad \forall a \in A. \end{align} $$

   In turn, (3.28)–(3.30) are equivalent to the same set of conditions with (3.28) replaced by

   (3.31) $$ \begin{align} (\Delta \otimes \mathsf{Id}_A) \widetilde{K} = R_{21} \widetilde{K}_{13} R_{21} \widetilde{K}_{23}. \end{align} $$

   Indeed, the forward direction follows from

   $$\begin{align*}\begin{array}{rll} (\Delta \otimes \mathsf{Id}_A) \widetilde{K} &\overset{\mathrm{(3.28)}}{=} \widetilde{K}_{23}R_{21} \widetilde{K}_{13} R_{21} &\overset{\mathrm{(3.29)}}{=} \widetilde{K}_{23} \big( (\mathsf{Id}_H \otimes \delta) \widetilde{K} \big)\\[.2pc] &\overset{\mathrm{(3.30)}}{=} \big( (\mathsf{Id}_H \otimes \delta) \widetilde{K} \big) \widetilde{K}_{23} & \overset{\mathrm{(3.29)}}{=} R_{21} \widetilde{K}_{13} R_{21} \widetilde{K}_{23}, \end{array} \end{align*}$$
   while the opposite direction is obtained by reversing the argument.

2. (b) Conditions (3.29), (3.30) and (3.31) are precisely the conditions for a quasitriangular comodule algebra used in [Kol20, Definition 2.7], with the only difference that [Kol20] works with right comodule algebras, while we work with left ones.

3. (c) Equating the right-hand sides of (3.28) and (3.31) gives that

   $$\begin{align*}\widetilde{K}_{23}R_{21} \widetilde{K}_{13} R_{21} = R_{21} \widetilde{K}_{13} R_{21} \widetilde{K}_{23}, \end{align*}$$

   from which it follows that $\widetilde {K}$ and R define representations of the braid groups of type B.

4 Reflective centers of module categories

In this part, we introduce and study the reflective center of a module category ${\mathcal {M}}$ over a braided monoidal category ${\mathcal {C}}$ . Preliminary results on this construction are presented in Section 4.1. Then, in Section 4.2, we realize the reflective center of ${\mathcal {M}}$ as a center of a certain ${\mathcal {C}}$ -bimodule category. This enables us to establish properties of reflective centers such as being abelian, finite and semisimple in the case when ${\mathcal {C}}$ is a braided tensor category.

4.1 Preliminaries on reflective centers

We introduce the terminology below.

Definition 4.1. Let be a braided monoidal category, and let $({\mathcal {M}}, \triangleright , m, \lambda )$ be a left ${\mathcal {C}}$ -module category. The reflective center of ${\mathcal {M}}$ with respect to ${\mathcal {C}}$ is a category ${\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}})$ defined as follows.

1. (a) Its objects are pairs $(M, e^M)$ , where M is an object of ${\mathcal {M}}$ , and

   $$\begin{align*}e^M:=\{e^M_Y\colon Y \triangleright M \overset{\sim}{\to} Y \triangleright M\}_{Y \in {\mathcal{C}}} \quad (\textit{reflection}) \end{align*}$$
   is a natural isomorphism such that $e^M_{X \otimes Y} \; (= e_{X \otimes Y, M})$ satisfies (3.13) for all $X,Y \in {\mathcal {C}}$ .

2. (b) The morphisms $(M, e^M) \to (N, e^N)$ are given by morphisms $f \in \operatorname {Hom}_{{\mathcal {M}}}(M,N)$ such that, for all $Y \in {\mathcal {C}}$ ,

   $$ \begin{align*}(\mathsf{Id}_Y \triangleright f) \circ e^M_Y = e^N_Y \circ (\mathsf{Id}_Y \triangleright f).\end{align*} $$

Lemma 4.2. Retain the notation above. We have that ${\mathcal {E}}_{\mathcal {C}}({\mathcal {M}})$ is a left ${\mathcal {C}}$ -module category, where by the abusing notation $\triangleright $ , the action bifunctor $\triangleright : {\mathcal {C}} \times {\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}}) \to {\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}})$ is defined by

$$ \begin{align*}Y \triangleright (M,e^M):=(Y \triangleright M,\; e^{Y \triangleright M}),\end{align*} $$

where $e^{Y \triangleright M}_X \; (= e_{X, Y \triangleright M})$ is defined by (3.14) for all $X,Y \in {\mathcal {C}}$ , and the associativity isomorphism is that of the left ${\mathcal {C}}$ -module category ${\mathcal {M}}$ .

Proof. First, we need to show that $\triangleright $ is well defined on objects and on morphisms.

Given objects $W,X,Y \in {\mathcal {C}}$ and $M \in {\mathcal {M}}$ , we need to show that $e^{Y \triangleright M}_{W \otimes X}$ defined by (3.14) satisfies (3.13) as in Definition 4.1(a). This is achieved by the following computation:

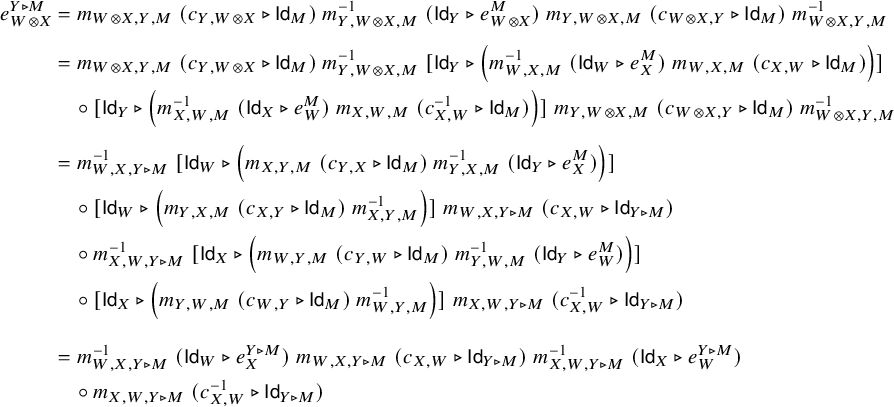$$ \begin{align*} e^{Y \triangleright M}_{W \otimes X} &= m_{W \otimes X,Y,M} \; (c_{Y,W \otimes X} \triangleright \mathsf{Id}_M) \; m_{Y,W \otimes X,M}^{-1} \; (\mathsf{Id}_Y \triangleright e_{W \otimes X}^M) \; m_{Y,W \otimes X,M} \; (c_{W \otimes X,Y} \triangleright \mathsf{Id}_M) \; m_{W \otimes X,Y,M}^{-1}\\[4pt] &= m_{W \otimes X,Y,M} \; (c_{Y,W \otimes X} \triangleright \mathsf{Id}_M) \; m_{Y,W \otimes X,M}^{-1} \; [\mathsf{Id}_Y \triangleright \left(m_{W,X,M}^{-1} \; (\mathsf{Id}_W \triangleright e_X^M) \; m_{W,X,M} \; (c_{X,W} \triangleright \mathsf{Id}_M)\right)] \\ &\quad \circ [\mathsf{Id}_Y \triangleright \left(m_{X,W,M}^{-1} \; (\mathsf{Id}_X \triangleright e_W^M) \; m_{X,W,M}\; (c_{X,W}^{-1} \triangleright \mathsf{Id}_M)\right)] \; m_{Y,W \otimes X,M} \; (c_{W \otimes X,Y} \triangleright \mathsf{Id}_M) \; m_{W \otimes X,Y,M}^{-1}\\[4pt] &= m_{W,X,{Y \triangleright M}}^{-1} \; [\mathsf{Id}_W \triangleright \left( m_{X,Y,M} \; (c_{Y,X} \triangleright \mathsf{Id}_M) \; m_{Y,X,M}^{-1} \; (\mathsf{Id}_Y \triangleright e_X^M)\right)] \\ & \quad \circ [\mathsf{Id}_W \triangleright \left(m_{Y,X,M} \; (c_{X,Y} \triangleright \mathsf{Id}_M) \; m_{X,Y,M}^{-1} \right)] \; m_{W,X,{Y \triangleright M}} \; (c_{X,W} \triangleright \mathsf{Id}_{Y \triangleright M}) \\ &\quad \circ m_{X,W,{Y \triangleright M}}^{-1} \; [\mathsf{Id}_X \triangleright \left( m_{W,Y,M} \; (c_{Y,W} \triangleright \mathsf{Id}_M) \; m_{Y,W,M}^{-1} \; (\mathsf{Id}_Y \triangleright e_W^M)\right)] \\ & \quad \circ [\mathsf{Id}_X \triangleright \left(m_{Y,W,M} \; (c_{W,Y} \triangleright \mathsf{Id}_M) \; m_{W,Y,M}^{-1} \right)] \; m_{X,W,{Y \triangleright M}}\; (c_{X,W}^{-1} \triangleright \mathsf{Id}_{Y \triangleright M}) \\[8pt] &= m_{W,X,{Y \triangleright M}}^{-1} \; (\mathsf{Id}_W \triangleright e_X^{Y \triangleright M}) \; m_{W,X,{Y \triangleright M}} \; (c_{X,W} \triangleright \mathsf{Id}_{Y \triangleright M}) \; m_{X,W,{Y \triangleright M}}^{-1} \; (\mathsf{Id}_X \triangleright e_W^{Y \triangleright M}) \\ &\quad \circ m_{X,W,{Y \triangleright M}}\; (c_{X,W}^{-1} \triangleright \mathsf{Id}_{Y \triangleright M}) \end{align*} $$

Here, the first and last equations hold by (3.14); the second equation holds by Definition 4.1(b) for $e^M$ ; and the third equation follows from (3.1), from the braid axiom (2.1), and the naturality of c. A similar computation shows that the original associativity isomorphism $m_{X,Y,M}$ indeed defines a morphism in ${\mathcal {E}}_{\mathcal {C}}({\mathcal {M}})$ .

Next, given an object $X \in {\mathcal {C}}$ , along with morphisms $f:Y \to Y'$ in ${\mathcal {C}}$ and $g:M \to M'$ in ${\mathcal {M}}$ , we need to show that $(\mathsf {Id}_X \triangleright (f \triangleright g))\circ e^{Y \triangleright M}_X = e^{Y' \triangleright M'}_X \circ (\mathsf {Id}_X \triangleright (f \triangleright g))$ as in Definition 4.1(b). This is done as follows:

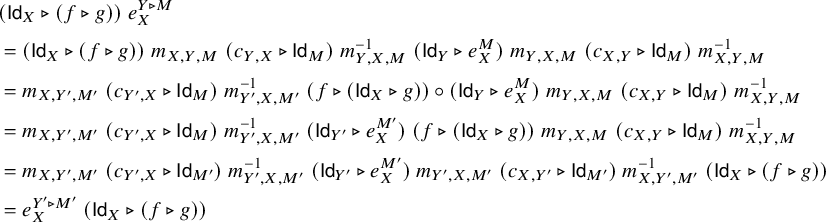$$ \begin{align*} &(\mathsf{Id}_X \triangleright (f \triangleright g))\; e^{Y \triangleright M}_X\\[2pt] &= (\mathsf{Id}_X \triangleright (f \triangleright g))\; m_{X,Y,M} \; (c_{Y,X} \triangleright \mathsf{Id}_M) \; m_{Y,X,M}^{-1} \; (\mathsf{Id}_Y \triangleright e_X^M)\; m_{Y,X,M} \; (c_{X,Y} \triangleright \mathsf{Id}_M) \; m_{X,Y,M}^{-1}\\[2pt] &= m_{X,Y',M'} \; (c_{Y',X} \triangleright \mathsf{Id}_M) \; m_{Y',X,M'}^{-1} \; (f \triangleright (\mathsf{Id}_X \triangleright g))\circ (\mathsf{Id}_Y \triangleright e_X^M)\; m_{Y,X,M} \; (c_{X,Y} \triangleright \mathsf{Id}_M) \; m_{X,Y,M}^{-1}\\[2pt] &= m_{X,Y',M'} \; (c_{Y',X} \triangleright \mathsf{Id}_M) \; m_{Y',X,M'}^{-1} \; (\mathsf{Id}_{Y'} \triangleright e_X^{M'})\; (f \triangleright (\mathsf{Id}_X \triangleright g)) \; m_{Y,X,M} \; (c_{X,Y} \triangleright \mathsf{Id}_M) \; m_{X,Y,M}^{-1}\\[2pt] &= m_{X,Y',M'} \; (c_{Y',X} \triangleright \mathsf{Id}_{M'}) \; m_{Y',X,M'}^{-1} \; (\mathsf{Id}_{Y'} \triangleright e_X^{M'})\; m_{Y',X,M'} \; (c_{X,Y'} \triangleright \mathsf{Id}_{M'}) \; m_{X,Y',M'}^{-1} \; (\mathsf{Id}_X \triangleright (f \triangleright g))\\[2pt] &=e^{Y' \triangleright M'}_X \; (\mathsf{Id}_X \triangleright (f \triangleright g)) \end{align*} $$

Here, the first and last equations hold by (3.14); the second and fourth equations hold by the naturality of m and of c; and the third equation holds by Definition 4.1(b) for $e^M$ .

Therefore, the ${\mathcal {C}}$ -action bifunctor $\triangleright $ for ${\mathcal {E}}_{\mathcal {C}}({\mathcal {M}})$ is well defined. It also satisfies (3.1) and (3.2) because they are satisfied for the ${\mathcal {C}}$ -action bifunctor for ${\mathcal {M}}$ .

An important feature of ${\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}})$ is that the reflections $e^M$ in Definition 4.1(a) equip this module category with a braiding (as in Section 3.5).

Proposition 4.3. Take a braided monoidal category $({\mathcal {C}},c)$ and a left ${\mathcal {C}}$ -module category ${\mathcal {M}}$ . Then, the reflective center ${\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}})$ is a braided left ${\mathcal {C}}$ -module category, where

for $Y \in {\mathcal {C}}$ and $(M,e^M) \in {\mathcal {E}}_{\mathcal {C}}({\mathcal {M}})$ . Here, $Y \triangleright (M,e^M):= (Y \triangleright M, \;e^{Y \triangleright M})$ by Lemma 4.2.

Proof. We have that ${\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}})$ is a left ${\mathcal {C}}$ -module category by Lemma 4.2. So, it suffices to show that $e_{Y,(M, e^M)}:=e^M_Y$ is a braiding for ${\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}})$ . First, we verify that $e^M_Y$ is a morphism in ${\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}})$ . We compute that, for all $X,Y\in {\mathcal {C}}$ and $M \in {\mathcal {M}}$ ,

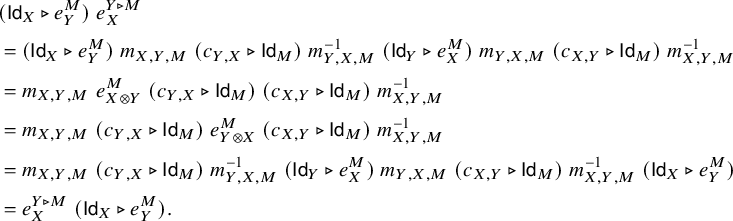$$ \begin{align*} &(\mathsf{Id}_X \triangleright e^M_Y) \; e^{Y \triangleright M}_X\\[2pt] &= (\mathsf{Id}_X \triangleright e_Y^M) \; m_{X,Y,M} \; (c_{Y,X} \triangleright \mathsf{Id}_M) \; m_{Y,X,M}^{-1} \; (\mathsf{Id}_Y \triangleright e_X^M) \; m_{Y,X,M} \; (c_{X,Y} \triangleright \mathsf{Id}_M) \; m_{X,Y,M}^{-1}\\[2pt] &= m_{X,Y,M} \; e_{X \otimes Y}^M \; (c_{Y,X} \triangleright \mathsf{Id}_M) \; (c_{X,Y} \triangleright \mathsf{Id}_M) \; m_{X,Y,M}^{-1}\\[2pt] &= m_{X,Y,M} \; (c_{Y,X} \triangleright \mathsf{Id}_M) \; e_{Y \otimes X}^M \; (c_{X,Y} \triangleright \mathsf{Id}_M) \; m_{X,Y,M}^{-1}\\[2pt] &= m_{X,Y,M} \; (c_{Y,X} \triangleright \mathsf{Id}_M) \; m^{-1}_{Y,X,M} \; (\mathsf{Id}_Y \triangleright e_X^M)\; m_{Y,X,M} \;(c_{X,Y} \triangleright \mathsf{Id}_M) \; m^{-1}_{X,Y,M} \; (\mathsf{Id}_X \triangleright e_Y^M)\\[2pt] &= e^{Y \triangleright M}_X \; (\mathsf{Id}_X \triangleright e^M_Y). \end{align*} $$

The first and last equations hold by Lemma 4.2. The second and fourth equations hold by Definition 4.1(a). The third equation holds by the naturality of c in the first slot.

Now we are done since the morphism $e^M_Y$ of ${\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}})$ is an isomorphism by Definition 4.1(a), and it also satisfies the first braided module category axiom (3.13) by Definition 4.1(a) and the second braided module category axiom (3.14) by Lemma 4.2.

4.2 Reflective centers as centers of bimodule categories

Given a braided monoidal category $({\mathcal {C}},c)$ , any left ${\mathcal {C}}$ -module category $({\mathcal {M}},\triangleright ,m,\lambda )$ is also a right ${\mathcal {C}}$ -module category $({\mathcal {M}},\triangleleft ,n,\rho )$ , where for all $X,Y\in {\mathcal {C}}$ , $M\in {\mathcal {M}}$ , we define

$$ \begin{align*} M\triangleleft X:= X\triangleright M, \end{align*} $$

and we define the structure morphisms $n_{M,X,Y}$ , $\rho _{M}$ , $b_{X,M,Y}$ as follows:

We denote the data $\left ({\mathcal {M}}, \; \triangleright , \; \triangleleft :=\triangleright , \;m, \;n:=m(c \triangleright \mathsf {Id}), \;\lambda , \;\rho :=\lambda , \; b:=m(c^{-1} \triangleright \mathsf {Id})m^{-1}\right )$ by ${\mathcal {M}}_{\mathrm {bim}}$ , and this is referred to as a one-sided bimodule category.

Lemma 4.4. Given the setting above, we have the following statements:

1. (a) ${\mathcal {M}}_{\mathrm {bim}}$ is a ${\mathcal {C}}$ -bimodule category and thus is a left $({\mathcal {C}} \boxtimes {\mathcal {C}}^{\otimes \mathrm {op}})$ -module category.

2. (b) If ${\mathcal {M}}$ is an exact left ${\mathcal {C}}$ -module category, then ${\mathcal {M}}_{\mathrm {bim}}$ is an exact left $({\mathcal {C}} \boxtimes {\mathcal {C}}^{\otimes \mathrm {op}})$ -module category.

Proof. Part (a) follows from [Gre10, Proposition 7.1]; see also Remark 3.9. Part (b) follows from remarks in [DN13, Equation 18].

Next, recall the notion of a center of a bimodule category from Definition 3.10, and consider the connection to reflective centers below.

Proposition 4.5. Retain the notation above. Then we have that ${\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}})$ and ${\mathcal {Z}}_{{\mathcal {C}}}({\mathcal {M}}_{\mathrm {bim}})$ are isomorphic as categories.

Proof. Given an object $(M,e^M) \in {\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}})$ , we also get that $(M,d^M:=e^M) \in {\mathcal {Z}}_{{\mathcal {C}}}({\mathcal {M}}_{\mathrm {bim}})$ by setting $\triangleleft :=\triangleright $ , $n:=m(c \triangleright \mathsf {Id})$ , $\rho :=\lambda $ , $b:=m(c^{-1} \triangleright \mathsf {Id})m^{-1}$ (via Lemma 4.4). Indeed, (3.11) holds by the naturality of $e^M$ and by (3.13) as follows:

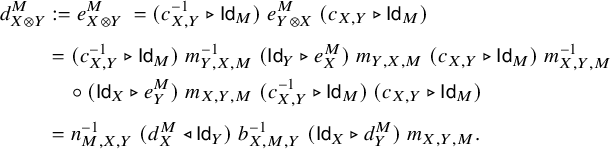$$ \begin{align*} d_{X \otimes Y}^M &:= e_{X \otimes Y}^M \; = (c^{-1}_{X,Y} \triangleright \mathsf{Id}_M) \; e_{Y \otimes X}^M \; (c_{X,Y} \triangleright \mathsf{Id}_M)\\[.3pc] &= (c^{-1}_{X,Y} \triangleright \mathsf{Id}_M) \; m_{Y,X,M}^{-1} \; (\mathsf{Id}_Y \triangleright e_X^M) \; m_{Y,X,M} \; (c_{X,Y} \triangleright \mathsf{Id}_M) \; m_{X,Y,M}^{-1}\\ & \quad \circ (\mathsf{Id}_X \triangleright e_Y^M) \; m_{X,Y,M}\; (c_{X,Y}^{-1} \triangleright \mathsf{Id}_M) \; (c_{X,Y} \triangleright \mathsf{Id}_M)\\[.3pc] & = n_{M,X,Y}^{-1} \; (d_{X}^{M}\triangleleft\mathsf{Id}_Y) \; b^{-1}_{X,M,Y} \; (\mathsf{Id}_X\triangleright d_{Y}^{M}) \; m_{X,Y,M}. \end{align*} $$

Conversely, given $(M,d^M) \in {\mathcal {Z}}_{{\mathcal {C}}}({\mathcal {M}}_{\mathrm {bim}})$ , we obtain that $(M,e^M:=d^M)$ is in ${\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}})$ by a similar argument. This identification of objects extends to an identification of morphisms in ${\mathcal {Z}}_{{\mathcal {C}}}({\mathcal {M}}_{\mathrm {bim}})$ (see Definition 3.10) with morphisms in ${\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}})$ (see Definition 4.1(b)). Thus, we have an isomorphism of categories: ${\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}}) \cong {\mathcal {Z}}_{{\mathcal {C}}}({\mathcal {M}}_{\mathrm {bim}})$ .

Corollary 4.6. We have the following statements about the reflective center ${\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}})$ , for ${\mathcal {C}}$ a braided tensor category and ${\mathcal {M}}$ a left ${\mathcal {C}}$ -module category:

1. (a) ${\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}})$ is a ${\mathcal {Z}}({\mathcal {C}})$ -module category.

2. (b) ${\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}}) \simeq \mathsf {Fun}_{{\mathcal {C}} \boxtimes {\mathcal {C}}^{\otimes \mathrm {op}}}({\mathcal {C}}, {\mathcal {M}}_{\mathrm {bim}})$ as ${\mathcal {Z}}({\mathcal {C}})$ -module categories.

3. (c) ${\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}})$ is abelian when ${\mathcal {M}}$ is exact and finite.

4. (d) ${\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}})$ is finite when ${\mathcal {C}}$ is finite and ${\mathcal {M}}$ is exact and finite.

5. (e) ${\mathcal {E}}_{{\mathcal {C}}}({\mathcal {M}})$ is semisimple when ${\mathcal {C}}$ and ${\mathcal {M}}$ are finite and semisimple.

Proof. It follows from Proposition 4.5 that it suffices to establish the statements for ${\mathcal {Z}}_{{\mathcal {C}}}({\mathcal {M}}_{\mathrm {bim}})$ . Part (a) then holds by [Gre10, Lemma 7.8]. We can then apply Proposition 4.5 to obtain the action of ${\mathcal {Z}}({\mathcal {C}})$ on ${\mathcal {E}}_{\mathcal {C}}({\mathcal {M}})$ below:

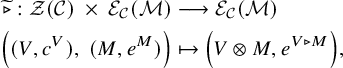$$ \begin{align*} \widetilde{\triangleright}: {\mathcal{Z}}({\mathcal{C}}) \;\times \;{\mathcal{E}}_{{\mathcal{C}}}({\mathcal{M}}) &\longrightarrow {\mathcal{E}}_{{\mathcal{C}}}({\mathcal{M}}) \\ \left( (V, c^V), \; (M, e^M) \right) & \mapsto \left( V \otimes M, e^{V \triangleright M}\right), \end{align*} $$

where, for any $X \in {\mathcal {C}}$ , we have

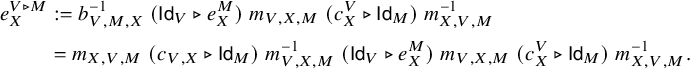$$ \begin{align*} e^{V \triangleright M}_X &:= b_{V,M,X}^{-1} \; (\mathsf{Id}_V \triangleright e_X^M) \; m_{V,X,M} \;(c_X^V \triangleright \mathsf{Id}_M) \; m_{X,V,M}^{-1}\\[.2pc] &= m_{X,V,M} \; (c_{V,X} \triangleright \mathsf{Id}_M)\; m^{-1}_{V,X,M} \;(\mathsf{Id}_V \triangleright e_X^M) \; m_{V,X,M} \; (c_X^V \triangleright \mathsf{Id}_M) \;m_{X,V,M}^{-1}. \end{align*} $$

For part (b), note that by [Gre10, Proposition 7.10], ${\mathcal {Z}}_{{\mathcal {C}}}({\mathcal {M}}_{\mathrm {bim}})$ is isomorphic to $\mathsf {Rex}_{{\mathcal {C}} \boxtimes {\mathcal {C}}^{\otimes ^{\mathrm {op}}}}({\mathcal {C}}, {\mathcal {M}}_{\mathrm {bim}})$ . We have that ${\mathcal {C}}$ is an exact module category over ${\mathcal {C}} \boxtimes {\mathcal {C}}^{\otimes ^{\mathrm {op}}}$ by Example 3.6. Now by Proposition 3.8, we have that $\mathsf {Rex}_{{\mathcal {C}} \boxtimes {\mathcal {C}}^{\otimes ^{\mathrm {op}}}}({\mathcal {C}}, {\mathcal {M}}_{\mathrm {bim}}) = \mathsf {Fun}_{{\mathcal {C}} \boxtimes {\mathcal {C}}^{\otimes ^{\mathrm {op}}}}({\mathcal {C}}, {\mathcal {M}}_{\mathrm {bim}})$ . So, the result holds.

By part (b), it suffices to establish parts (c,d,e) for $\mathsf {Fun}_{{\mathcal {C}} \boxtimes {\mathcal {C}}^{\otimes ^{\mathrm {op}}}}({\mathcal {C}}, {\mathcal {M}}_{\mathrm {bim}})$ . Parts (c,d) then follow from Example 3.6, Lemma 4.4(b), Propositions 3.7, 3.8. Part (e) follows from Proposition 3.5.

We note that the ${\mathcal {Z}}({\mathcal {C}})$ -module structure $\widetilde {\triangleright }$ on ${\mathcal {E}}_{\mathcal {C}}({\mathcal {M}})$ in Corollary 4.6(a) does not coincide with the one obtained by restricting the (braided) ${\mathcal {C}}$ -module structure $\triangleright $ of Lemma 4.2 and Proposition 4.3 along the tensor functor ${\mathcal {Z}}({\mathcal {C}})\to {\mathcal {C}}$ . However, the ${\mathcal {C}}$ -action $\triangleright $ can be recovered from $\widetilde {\triangleright }$ by restriction along the tensor functor ${\mathcal {C}}\to {\mathcal {Z}}({\mathcal {C}}), \, V\mapsto (V,c^V),$ where $c^V_{X} := c_{X,V}$ , for all $X\in {\mathcal {C}}$ .

5 Reflective algebras of comodule algebras

In this section, we consider the case when ${\mathcal {C}}$ is the braided monoidal category ${{H}\text {-}\mathsf {mod}}$ for H a quasitriangular Hopf algebra over $\mathbb {k}$ and ${\mathcal {M}}$ is the left ${\mathcal {C}}$ -module category ${{A}\text {-}\mathsf {mod}}$ , for a left H-comodule A over $\mathbb {k}$ . (Note that every indecomposable, exact ${\mathcal {C}}$ -module category is of this form in the finite tensor case [AM07, Proposition 1.19] – that is, when restricting to finite-dimensional modules over finite-dimensional A and H.) The module associativity isomorphism m given by the (trivial) associativity isomorphism of $\mathsf {Vec}$ . The goal of this section is to describe an H-comodule algebra $R_H(A)$ that represents the reflective center ${\mathcal {E}}_{\mathcal {C}}({\mathcal {M}})$ – that is, to get

$$\begin{align*}{\mathcal{E}}_{{{H}\text{-}\mathsf{mod}}}({{A}\text{-}\mathsf{mod}}) \; \cong \; {{R_H(A)}\text{-}\mathsf{mod}} \quad \text{as categories}. \end{align*}$$

The notation for the section and for the rest of the paper is summarized in Section 5.1. An intermediate category of Doi–Hopf modules is introduced in Section 5.2 toward achieving the isomorphism above. With this, we define $R_H(A)$ and establish the desired isomorphism in Section 5.3. Properties of $R_H(A)$ are examined in Section 5.4.

5.1 Standing notation and hypotheses for the Hopf setting

We collect for the reader notation and setting that we will use from now on. We use (sumless) Sweedler notation throughout.

• • $\otimes $ will denote the tensor product ( $\otimes _{\mathbb {k}}$ ), monoidal product ( $\otimes $ ) and ${\mathcal {C}}$ -action bifunctor ( $\triangleright $ ) above from now on as they are all equal $\otimes _{\mathbb {k}}$ .

• • $H:= (H,m,u,\Delta , \varepsilon ,S)$ is a quasitriangular Hopf algebra over $\mathbb {k}$ .

• • $\Delta (h) = h_{(1)} \otimes h_{(2)}$ is the coproduct of H. Its composition is denoted by

  $$\begin{align*}(\Delta \otimes \mathsf{Id}_H) \Delta(h) = (\mathsf{Id}_H \otimes \Delta) \Delta (h) =: h_{(1)} \otimes h_{(2)} \otimes h_{(3)}.\end{align*}$$

• • If H is finite-dimensional, then $\langle \hspace {0.02in}, \rangle $ is the Hopf pairing between $H^{*}$ and H. That is,

  (5.1) $$ \begin{align} \langle \xi \zeta, h \rangle = \langle \xi \otimes \zeta, \Delta(h) \rangle = \langle \xi, h_{(1)} \rangle \langle \zeta, h_{(2)} \rangle, \quad \langle \xi, h \ell \rangle = \langle \Delta(\xi), h \otimes \ell \rangle = \langle \xi_{(1)}, h \rangle \langle \xi_{(2)}, \ell \rangle, \end{align} $$
  for $\xi , \zeta \in H^{*}$ , $h, \ell \in H$ . Here, $\xi _{(1)} \otimes \xi _{(2)}$ denotes the coproduct of $\xi \in H^{*}$ .

• • If H is finite-dimensional, then we denote the dual basis of H by $\{h_d, \xi _d\}_d$ , for $h_d \in H$ and $\xi _d \in H^{*}$ . Namely, we get

  (5.2) $$ \begin{align} h = \textstyle \sum_d \langle \xi_d, h \rangle h_d, \quad \quad \quad \quad \xi = \sum_d \langle \xi, h_d \rangle \xi_d. \end{align} $$

• • If H is finite-dimensional, the standard left and right actions of H on $H^{*}$ are denoted by $\twoheadrightarrow $ and $\twoheadleftarrow $ , respectively. That is, for $h, h' \in H$ , $\xi \in H^{*}$ ,

  (5.3) $$ \begin{align} \begin{array}{c} h \twoheadrightarrow \xi= \langle \xi_{(2)}, h \rangle \xi_{(1)} \quad \text{with } \langle h \twoheadrightarrow \xi, h' \rangle := \langle \xi, h' h \rangle,\\[.3pc] \xi \twoheadleftarrow h := \langle \xi_{(1)}, h \rangle \xi_{(2)}\quad \text{with } \langle \xi \twoheadleftarrow h, h' \rangle := \langle \xi, h h' \rangle. \end{array} \end{align} $$

• • $R:=\sum _i s_i \otimes t_i \; \in H \otimes H$ is the R-matrix of H.

• • $R^{-1}:=\sum _i s^i \otimes t^i \; \in H \otimes H$ is the inverse of the R-matrix of H.

• • A is a left H-comodule algebra over $\mathbb {k}$ .

• • $\delta : A \to H \otimes A$ , $a \mapsto a_{[-1]} \otimes a_{[0]}$ , is the left H-coaction of A. Its composition is denoted by

  $$\begin{align*}(\Delta \otimes \mathsf{Id}_H) \delta(a) = (\mathsf{Id}_H \otimes \delta) \delta (a) =: a_{[-2]} \otimes a_{[-1]} \otimes a_{[0]}.\end{align*}$$

• • $K:=\sum _i g_i \otimes p_i \; \in H \otimes A$ is the K-matrix of A when A is quasitriangular.

• • $K^{-1}:=\sum _i g^i \otimes p^i \; \in H \otimes A$ is the inverse of the K-matrix of A when A is quasitriangular.

• • ${\mathcal {C}}$ is the braided monoidal category ${{H}\text {-}\mathsf {mod}}$ over $\mathbb {k}$ , with monoidal product $\otimes $ , unit object $\mathbb {k}$ and braiding c. The H-action for objects of ${\mathcal {C}}$ is denoted by a centered dot, $\cdot $ .

• • $c_{X,Y}:X \otimes Y \overset {\sim }{\to } Y \otimes X, \; x \otimes y \mapsto \sum _i (t_i \cdot y) \otimes (s_i \cdot x)$ , is the braiding of ${\mathcal {C}}$ via the R-matrix of H, for $X,Y \in {\mathcal {C}}$ .

• • $c^{-1}_{Y,X}: X \otimes Y \overset {\sim }{\to } Y \otimes X, \; x \otimes y \mapsto \sum _i (s^i \cdot y) \otimes (t^i \cdot x)$ , is the inverse braiding of ${\mathcal {C}}$ , via the inverse R-matrix of H, for $X,Y \in {\mathcal {C}}$ .

• • ${\mathcal {M}}$ is the left ${\mathcal {C}}$ -module category ${{A}\text {-}\mathsf {mod}}$ over $\mathbb {k}$ . The A-action for objects of ${\mathcal {M}}$ is denoted by an asterisk, $\ast $ , or by $\widetilde {\ast }$ if the action is induced.

• • $e^M$ is the braiding of ${\mathcal {M}} = {{A}\text {-}\mathsf {mod}}$ for $M \in {\mathcal {M}}$ .

• • $e^M_X(x \otimes m) := \sum _i (g_i \cdot x) \otimes (p_i \ast m)$ , for $X \in {\mathcal {C}}$ and $\sum _i g_i \otimes p_i \in H \otimes A$ .

• • When H (resp., A) is in the subscript of c or e, this indicates the regular left H-module (resp., A-module).

5.2 Reflective centers as Doi–Hopf modules

Here, we will consider a category of left Doi–Hopf modules, ${}^{\widehat {H}}_A \mathsf {DH}(H)$ , consisting of vector spaces which are modules over the left H-comodule algebra A and comodules over a left H-module coalgebra $\widehat {H}$ , which is a version of Majid’s covariantized (or transmuted) coalgebra [Maj91,Maj00]. Our main goal is to show that

(5.4) $$ \begin{align} {\mathcal{E}}_{\mathcal{C}}({\mathcal{M}}) \; \cong\; {}^{\widehat{H}}_A \mathsf{DH}(H)\quad \text{as categories.} \end{align} $$

We recall the category of Doi–Hopf modules in Section 5.2.1; we then get ${}^{\widehat {H}}_A \mathsf {DH}(H)$ after we define $\widehat {H}$ in Section 5.2.2. Next, we construct a functor $F: {\mathcal {E}}_{\mathcal {C}}({\mathcal {M}}) \to {}^{\widehat {H}}_A \mathsf {DH}(H)$ in Section 5.2.3 and a functor $G: {}^{\widehat {H}}_A \mathsf {DH}(H) \to {\mathcal {E}}_{\mathcal {C}}({\mathcal {M}}) $ in Section 5.2.4. Then, we establish (5.4) in Section 5.2.5.

5.2.1 The category of Doi–Hopf modules

First, let us recall the notion of a Doi–Hopf module from work of Doi [Doi92]. Note that we abuse some of the notation of Section 5.1 below.

Definition 5.5 [Doi92, Remark 1.3].

Consider the following input data:

• • L, a Hopf algebra;

• • B, a left L-comodule algebra with coaction given by $\delta : B \to L \otimes B, \; b \mapsto b_{[-1]} \otimes b_{[0]}$ ;

• • C, a left L-module coalgebra with action given by $\rightharpoonup : L \otimes C \to C$ .

A vector space M is a left $(L,B,C)$ -Doi–Hopf module is if the following conditions hold:

1. (i) M is a left B-module with action given by $\ast : B \otimes M \to M$ ;

2. (ii) M is a left C-comodule with coaction given by $\varphi : M \to C \otimes M, \; m \mapsto m_{-1} \otimes m_{0}$ ;

action and coaction are subject to the following compatibility condition,

(5.6) $$ \begin{align} (b \ast m)_{-1} \otimes (b \ast m)_{0} \; = \; (b_{[-1]} \rightharpoonup m_{-1}) \otimes (b_{[0]} \ast m_0), \end{align} $$

for all $m \in M$ and $b \in B$ .

The collection of left $(L,B,C)$ -Doi–Hopf modules forms a category. Here, a morphism between two left $(L,B,C)$ -Doi–Hopf modules is a map that is simultaneously a left B-module map and a left C-comodule map. We denote this category by

$$\begin{align*}{}^C_B \mathsf{DH}(L).\end{align*}$$

In the appendix of the arXiv version 1 of this article, it is shown that the category of left $(L,B,C)$ -Doi–Hopf modules admits a canonical structure of a left module category over the braided monoidal category ${{L}\text {-}\mathsf {mod}}$ when L is quasitriangular, with R-matrix $\sum _i s_i \otimes t_i$ .

5.2.2 The left H-module coalgebra $\widehat {H}$

Let us define the H-module coalgebra $\widehat {H}$ mentioned above in (5.4) which is a version of Majid’s transmuted (or covariantized) coalgebra; see Remark 5.8.

Definition 5.7. Take $\widehat {H}$ to be equal to H as vector spaces, and consider the following comultiplication, counit and left H-action formulae:

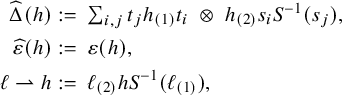$$ \begin{align*} \widehat{\Delta}(h) &:= \; \textstyle \sum_{i,j} t_j h_{(1)} t_i \;\otimes\; h_{(2)} s_i S^{-1}(s_j), \\ \widehat{\varepsilon}(h) &:= \; \varepsilon(h),\\ \ell \rightharpoonup h &:= \; \ell_{(2)} h S^{-1}(\ell_{(1)}), \end{align*} $$

for all $h \in \widehat {H}$ and $\ell \in H$ .

The operations from Definition 5.7 make $\widehat {H}$ a left H-module coalgebra. This follows as in [Maj00, Theorem 7.4.2].

Remark 5.8. The precise comparison to the conventions of [Maj00] is as follows. For a quasitriangular Hopf algebra $H:=(H, R:=\sum _i s_i \otimes t_i)$ , we have that its co-opposite Hopf algebra $H^{\mathrm {cop}}$ is a quasitriangular Hopf algebra with $R^{\mathrm {cop}}:=\sum _i t_i \otimes s_i$ . With this, and by inspecting the proof of [Maj91, Theorem 3.1], one can see that $(\widehat {H})^{\mathrm {cop}} = (H^{\mathrm {cop}})_{\mathrm {trm}}$ , where $H_{\mathrm {trm}}$ denotes the coalgebra obtained by transmutation in [Maj00, Theorem 7.4.2].

5.2.3 Functor from the reflective center to a category of Doi–Hopf modules

Consider the following preliminary result.

Lemma 5.9. Let $r_h$ be right multiplication by $h \in H$ . Then, the operator

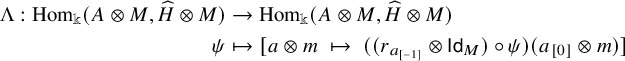$$ \begin{align*} \Lambda: \operatorname{Hom}_{\mathbb{k}}(A \otimes M, \widehat{H} \otimes M) &\to \operatorname{Hom}_{\mathbb{k}}(A \otimes M, \widehat{H} \otimes M)\\ \psi &\mapsto [a \otimes m \;\mapsto \; ((r_{a_{[-1]}} \otimes \mathsf{Id}_M) \circ\psi)(a_{[0]} \otimes m)] \end{align*} $$

is invertible, with inverse

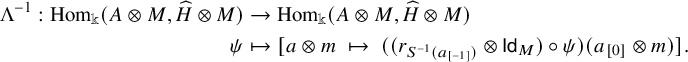$$ \begin{align*} \Lambda^{-1}: \operatorname{Hom}_{\mathbb{k}}(A \otimes M, \widehat{H} \otimes M) &\to \operatorname{Hom}_{\mathbb{k}}(A \otimes M, \widehat{H} \otimes M)\\ \psi &\mapsto [a \otimes m \;\mapsto \; ((r_{S^{-1}(a_{[-1]})} \otimes \mathsf{Id}_M) \circ\psi)(a_{[0]} \otimes m)]. \end{align*} $$

Next, we turn our attention to the desired functor for this section.

Proposition 5.10. We have a functor

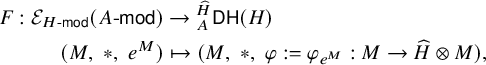$$ \begin{align*} F: {\mathcal{E}}_{{{H}\text{-}\mathsf{mod}}}({{A}\text{-}\mathsf{mod}}) &\to {}_A^{\widehat{H}} \mathsf{DH}(H)\\ (M, \; \ast, \; e^M) &\mapsto (M, \; \ast, \; \varphi:=\varphi_{e^M}: M \to \widehat{H} \otimes M), \end{align*} $$

where $\varphi (m) = e_{H}^M(1_H \otimes m)=: m_{-1} \otimes m_0$ .

Proof. It suffices to establish the following statements:

1. (i) $(M ,\varphi ) \in {{\widehat {H}}\text {-}\mathsf {comod}}$ (this will follow from (3.13)), and

2. (ii) $(M,\ast , \varphi )$ satisfies (5.6) (this will follow from $e_X^M \in {{A}\text {-}\mathsf {mod}}$ for any $X \in {{H}\text {-}\mathsf {mod}}$ ).

Toward (i), for $h, \ell \in H$ (as the regular left H-module), note that

(5.11) $$ \begin{align} c_{H,H}(h \otimes \ell) = \textstyle \sum_i t_i \ell \otimes s_i h \quad \quad \text{and} \quad \quad c^{-1}_{H,H}(h \otimes \ell) = \textstyle \sum_i s^i \ell \otimes t^i h. \end{align} $$

Moreover by taking $r_h: H \to H$ to be right multiplication by h, we get that $r_h \in {{H}\text {-}\mathsf {mod}}$ . Thus, by the naturality of $e^M$ , we obtain that

(5.12) $$ \begin{align} e_{H}^M(h \otimes m) \; = \; e_{H}^M(r_h \otimes \mathsf{Id}_M)(1_H \otimes m) \; = \; (r_h \otimes \mathsf{Id}_M)e_{H}^M(1_H \otimes m) \; = \; m_{-1}h \otimes m_0. \end{align} $$

Moreover, note that $\widehat {\Delta } = \omega \circ \Delta $ for

(5.13) $$ \begin{align} \omega(h \otimes h') := \textstyle \sum_{k,l} t_l h t_k \; \otimes \; h' s_k S^{-1}(s_l). \end{align} $$

In fact, as an aside, we have that $\omega $ is invertible with

(5.14) $$ \begin{align} \omega^{-1}(h \otimes h') := \textstyle \sum_{i,j} \; t^i h t^j \; \otimes \; h' S^{-1}(s^i) s^j. \end{align} $$

Now (i) holds by the following computation:

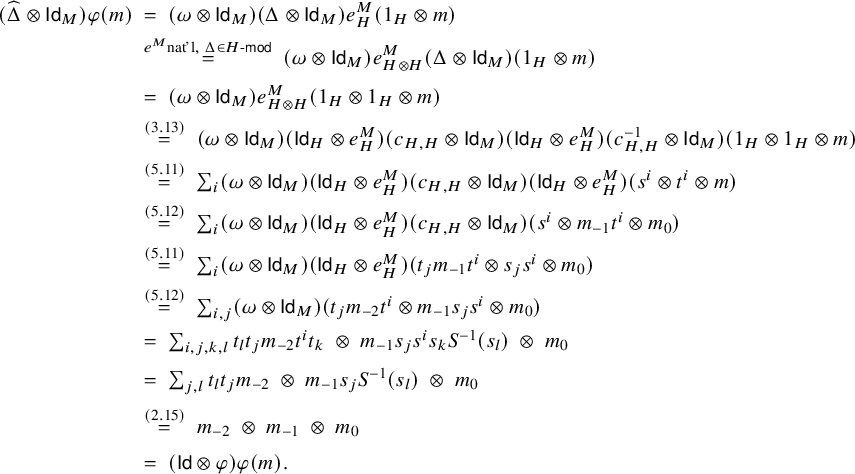$$ \begin{align*} (\widehat{\Delta} \otimes \mathsf{Id}_M)\varphi(m) & \; = \; (\omega \otimes \mathsf{Id}_M)(\Delta \otimes \mathsf{Id}_M)e_H^M(1_H \otimes m) \\ & \; \overset{e^M \text{nat'l},\ \Delta \in {{H}\text{-}\mathsf{mod}}}{=} \; (\omega \otimes \mathsf{Id}_M)e_{H\otimes H}^M(\Delta \otimes \mathsf{Id}_M)(1_H \otimes m)\\[.2pc] & \; = \; (\omega \otimes \mathsf{Id}_M)e_{H\otimes H}^M(1_H \otimes 1_H \otimes m)\\ & \; \overset{\mathrm{(3.13)}}{=} \; (\omega \otimes \mathsf{Id}_M)(\mathsf{Id}_H \otimes e_H^M)(c_{H,H} \otimes \mathsf{Id}_M)(\mathsf{Id}_H \otimes e_H^M)(c_{H,H}^{-1} \otimes \mathsf{Id}_M)(1_H \otimes 1_H \otimes m)\\ & \; \overset{\mathrm{(5.11)}}{=} \; \textstyle \sum_i(\omega \otimes \mathsf{Id}_M)(\mathsf{Id}_H \otimes e_H^M)(c_{H,H} \otimes \mathsf{Id}_M)(\mathsf{Id}_H \otimes e_H^M)(s^i \otimes t^i \otimes m)\\ & \; \overset{\mathrm{(5.12)}}{=} \; \textstyle \sum_i(\omega \otimes \mathsf{Id}_M)(\mathsf{Id}_H \otimes e_H^M)(c_{H,H} \otimes \mathsf{Id}_M)(s^i \otimes m_{-1}t^i \otimes m_0)\\ & \; \overset{\mathrm{(5.11)}}{=} \; \textstyle \sum_i(\omega \otimes \mathsf{Id}_M)(\mathsf{Id}_H \otimes e_H^M)(t_jm_{-1}t^i \otimes s_js^i \otimes m_0) \\ & \; \overset{\mathrm{(5.12)}}{=} \; \textstyle \sum_{i,j}(\omega \otimes \mathsf{Id}_M)(t_jm_{-2}t^i \otimes m_{-1}s_js^i \otimes m_0) \\& \; = \; \textstyle \sum_{i,j,k,l} t_l t_j m_{-2} t^i t_k \; \otimes \; m_{-1} s_j s^i s_k S^{-1}(s_l) \; \otimes \; m_0\\[.2pc] & \; = \; \textstyle \sum_{j,l} t_l t_j m_{-2} \; \otimes \; m_{-1} s_j S^{-1}(s_l) \; \otimes \; m_0\\[.2pc] & \;\overset{\mathrm{(2.15)}}{=} \; m_{-2} \; \otimes \; m_{-1} \; \otimes \; m_0 \\[.2pc] & \; = \; (\mathsf{Id} \otimes \varphi)\varphi(m). \end{align*} $$

To prove (ii), note that $e_{H}^M \in {{A}\text {-}\mathsf {mod}}$ (). So, for $a \in A$ and $m \in M$ , we get that

(5.15)

Now the following computation verifies (ii):

At , we applied the operator $\Lambda ^{-1}$ from Lemma 5.9 to (5.15). This concludes the proof.

5.2.4 Functor from a category of Doi–Hopf modules to the reflective center

Proposition 5.16. For $\varphi (m):=m_{-1} \otimes m_0$ , we have a functor

$$ \begin{align*} G: {}_A^{\widehat{H}} \mathsf{DH}(H) &\to {\mathcal{E}}_{{{H}\text{-}\mathsf{mod}}}({{A}\text{-}\mathsf{mod}})\\[4pt] \left(M, \; \ast, \; \varphi: M \to \widehat{H} \otimes M\right) &\mapsto \left(M, \; \ast, \; e_X^M:=(e_X^M)_{\varphi}: X \otimes M \to X \otimes M\right), \end{align*} $$

where $e_X^M(x \otimes m) = (m_{-1} \cdot x) \otimes m_0$ , for $(X, \cdot )$ a left H-module.

Proof. It suffices to establish the following statements:

1. (i) $e_X^M$ satisfies (3.13) (this will follow from $(M ,\varphi ) \in {{\widehat {H}}\text {-}\mathsf {comod}}$ ), and

2. (ii) $e_X^M \in {{A}\text {-}\mathsf {mod}}$ for any $X \in {{H}\text {-}\mathsf {mod}}$ (this will follow from (5.6)).

To verify (i), recall the invertible linear map $\omega $ from (5.13) and (5.14), and recall that $\widehat {\Delta } = \omega \circ \Delta $ for the coproduct $\widehat {\Delta }$ in Definition 5.7. We use the Sweedler notation $\widehat {\Delta }(h):= h_{\widehat {(1)}} \otimes h_{\widehat {(2)}}$ for $h \in \widehat {H}$ , along with $\Delta (h):= h_{(1)} \otimes h_{(2)}$ for $h \in H$ . Also, for $X,Y \in {{H}\text {-}\mathsf {mod}}$ , and $x \in X$ , $y \in Y$ , we have that

(5.17) $$ \begin{align} c_{Y,X}(y \otimes x) = \textstyle \sum_i (t_i \cdot x) \otimes (s_i \cdot y) \quad \quad \text{and} \quad \quad c^{-1}_{Y,X}(x \otimes y) = \textstyle \sum_i (s^i \cdot y) \otimes (t^i \cdot x). \end{align} $$

Now (i) holds via the computation below for $X,Y \in {{H}\text {-}\mathsf {mod}}$ , $M \in {{A}\text {-}\mathsf {mod}}$ , $x \in X$ , $y \in Y$ , $m \in M$ :

$$ \begin{align*} e_{X \otimes Y}^M(x \otimes y \otimes m) & \; = \; (m_{-1} \cdot (x \otimes y)) \; \otimes \; m_0\\[.2pc] & \; = \; ((m_{-1})_{(1)} \cdot x)\; \otimes \;((m_{-1})_{(2)} \cdot y)\; \otimes\; m_0\\ & \; \overset{\mathrm{(5.14)}}{=} \; \textstyle \sum_{i,j} \; [t^i\;(m_{-1})_{\widehat{(1)}} \; t^j \cdot x]\; \otimes \;[(m_{-1})_{\widehat{(2)}} \; S^{-1}(s^i) \; s^j \cdot y] \; \otimes\; m_0\\ & \; \overset{\varphi\ \in {{\widehat{H}}\text{-}\mathsf{comod}}}{=} \; \textstyle \sum_{i,j} \; [t^i\;m_{-2} \; t^j \cdot x]\; \otimes \;[m_{-1} \; S^{-1}(s^i) \; s^j \cdot y] \; \otimes\; m_0\\ & \; \overset{\mathrm{(2.15)}}{=} \; \textstyle \sum_{i,j} \; [t_i \;m_{-2} \; t^j \cdot x]\; \otimes \;[m_{-1} \; s_i \; s^j \cdot y] \; \otimes\; m_0\\ & \; \overset{\mathrm{(5.12)}}{=} \; \textstyle \sum_{i,j} (\mathsf{Id}_X \otimes e_Y^M)[ t_i \; m_{-1} \; t^j \cdot x) \otimes (s_i\; s^j \cdot y)\otimes m_0\\ & \; \overset{\mathrm{(5.17)}}{=} \; \textstyle \sum_j (\mathsf{Id}_X \otimes e_Y^M)(c_{Y,X} \otimes \mathsf{Id}_M)[(s^j \cdot y) \otimes (m_{-1} t^j \cdot x) \otimes m_0]\\ & \; \overset{\mathrm{(5.12)}}{=} \; \textstyle \sum_j (\mathsf{Id}_X \otimes e_Y^M)(c_{Y,X} \otimes \mathsf{Id}_M)(\mathsf{Id}_Y \otimes e_X^M)[(s^j \cdot y) \otimes (t^j \cdot x) \otimes m]\\ & \; \overset{\mathrm{(5.17)}}{=} \; (\mathsf{Id}_X \otimes e_Y^M)(c_{Y,X} \otimes \mathsf{Id}_M)(\mathsf{Id}_Y \otimes e_X^M)(c_{Y,X}^{-1} \otimes \mathsf{Id}_M)(x \otimes y \otimes m). \end{align*} $$

Toward (ii), note that, for $a \in A$ and $m \in M$ , we get that

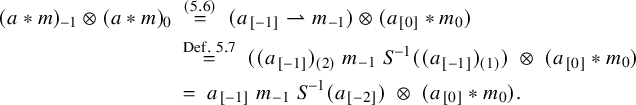$$ \begin{align*} (a \ast m)_{-1} \otimes (a \ast m)_{0} &\; \overset{\mathrm{(5.6)}}{=} \; (a_{[-1]} \rightharpoonup m_{-1}) \otimes (a_{[0]} \ast m_0) \nonumber\\ &\; \overset{\mathrm{Def.\;5.7}}{=} \; ((a_{[-1]})_{(2)} \; m_{-1} \; S^{-1}((a_{[-1]})_{(1)}) \; \otimes \; (a_{[0]} \ast m_0) \\ & \; =\; a_{[-1]} \; m_{-1} \; S^{-1}(a_{[-2]}) \; \otimes\; (a_{[0]} \ast m_0). \end{align*} $$

By the counit and antipode axioms, we get that

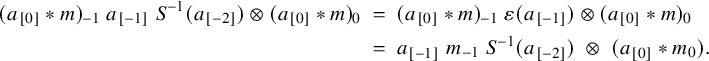$$ \begin{align*} (a_{[0]} \ast m)_{-1} \; a_{[-1]} \; S^{-1}(a_{[-2]}) \otimes (a_{[0]} \ast m)_{0} &\; = \;(a_{[0]} \ast m)_{-1} \; \varepsilon(a_{[-1]}) \otimes (a_{[0]} \ast m)_{0}\\ &\; = \; a_{[-1]} \; m_{-1} \; S^{-1}(a_{[-2]}) \; \otimes\; (a_{[0]} \ast m_0). \end{align*} $$

Applying the operator $\Lambda $ from Lemma 5.9 to the above equation yields

$$ \begin{align*} (a_{[0]} \ast m)_{-1} \; a_{[-1]} \; S^{-1}(a_{[-2]}) \; a_{[-3]}\otimes (a_{[0]} \ast m)_{0} \; = \; a_{[-1]} \; m_{-1} \; S^{-1}(a_{[-2]}) \; a_{[-3]} \; \otimes\; (a_{[0]} \ast m_0). \end{align*} $$

Using antipode and counit axioms again yields

$$ \begin{align*} (a_{[0]} \ast m)_{-1} \; a_{[-1]} \; \otimes \; (a_{[0]} \ast m)_0 \; = \; a_{[-1]} m_{-1} \; \otimes (a_{[0]} \ast m_0). \end{align*} $$

Now (ii) follows from the following computation:

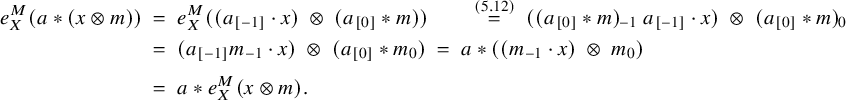$$ \begin{align*} e_X^M(a \ast (x \otimes m)) & \; = \; e_X^M((a_{[-1]} \cdot x) \; \otimes \; (a_{[0]} \ast m)) \hspace{.27in} \overset{\mathrm{(5.12)}}{=} \; ((a_{[0]} \ast m)_{-1} \; a_{[-1]} \cdot x) \; \otimes \; (a_{[0]} \ast m)_{0} \\ & \; = \; (a_{[-1]} m_{-1} \cdot x) \; \otimes \; (a_{[0]} \ast m_0) \; = \; a \ast ((m_{-1} \cdot x) \; \otimes \; m_0)\\[.2pc] & \; = \; a \ast e_X^M(x \otimes m). \end{align*} $$

This concludes the proof of the result.

5.2.5 Isomorphism of categories

Now we establish the category isomorphism (5.4).

Proposition 5.18. We have that the reflective center ${\mathcal {E}}_{{{H}\text {-}\mathsf {mod}}}({{A}\text {-}\mathsf {mod}})$ and the category of Doi–Hopf modules ${}^{\widehat {H}}_A \mathsf {DH}(H)$ are isomorphic as categories.

Proof. It suffices to show that the functors $F: {\mathcal {E}}_{{{H}\text {-}\mathsf {mod}}}({{A}\text {-}\mathsf {mod}}) \to {}^{\widehat {H}}_A \mathsf {DH}(H)$ from Proposition 5.10 and $G: {}^{\widehat {H}}_A \mathsf {DH}(H) \to {\mathcal {E}}_{{{H}\text {-}\mathsf {mod}}}({{A}\text {-}\mathsf {mod}})$ from Proposition 5.16, are mutually inverse. Starting with an object $(M,e^M)$ in ${\mathcal {E}}_{{{H}\text {-}\mathsf {mod}}}({{A}\text {-}\mathsf {mod}})$ , consider the half-braiding ${\overline {{e}}}$ on $GF(M,e^M)$ given by

$$ \begin{align*}{\overline{{e}}}^M_X(x\otimes m)=(m_{-1}\cdot x)\otimes m_0,\end{align*} $$

for $X \in {{H}\text {-}\mathsf {mod}}$ and $x \in X$ . Here, $m_{-1}\otimes m_0:=e_H^M(1_H\otimes m)$ . For $x\in X$ , take the morphism

$$ \begin{align*}l_x\colon H\to X, \quad h\mapsto h\cdot x \quad \in {{H}\text{-}\mathsf{mod}}.\end{align*} $$

Applying naturality of the braiding $e^M$ to $l_x$ gives

$$ \begin{align*}{\overline{{e}}}^M_X(x\otimes m) \; = \; (l_x\otimes \mathsf{Id}_M)e_H^M(1_H\otimes m) \;= \;e_X^M(l_x\otimes \mathsf{Id}_M)(1_H\otimes m) \;= \;e_X^M(1_H\cdot x\otimes m) \;= \; e_X^M(x\otimes m).\end{align*} $$

Hence, ${\overline {{e}}}=e$ , and the identity $GF(M)\to M$ is a morphism of objects in ${\mathcal {E}}_{{{H}\text {-}\mathsf {mod}}}({{A}\text {-}\mathsf {mod}})$ . This shows $GF=\mathsf {Id}_{{\mathcal {E}}_{{{H}\text {-}\mathsf {mod}}}({{A}\text {-}\mathsf {mod}})}$ .

However, for an object M in ${}^{\widehat {H}}_A \mathsf {DH}(H)$ with coaction $M\to \widehat {H}\otimes M, m\mapsto m_{-1}\otimes m_0$ , consider the induced $\widehat {H}$ -coaction ${\overline {{\varphi }}}$ on M obtained on $FG(M)$ . Then

$$ \begin{align*}{\overline{{\varphi}}}(m) \; = \;e_H^{G(M)}(1_H\otimes m) \;= \; (m_{-1}\cdot 1_H)\otimes m_0 \;= \; m_{-1}\otimes m_0.\end{align*} $$

This shows that $(FG(M),{\overline {{\varphi }}})=(M,\varphi )$ as Doi–Hopf modules, and hence, $FG = \mathsf {Id}_{{}^{\widehat {H}}_A \mathsf {DH}(H)}$ .

5.3 Reflective centers represented by reflective algebras

The goal of this section is to extend the isomorphism (5.4) to the isomorphism below:

(5.19) $$ \begin{align} {\mathcal{E}}_{\mathcal{C}}({\mathcal{M}}) \; \cong\; {}^{\widehat{H}}_A \mathsf{DH}(H) \; \cong\; {{R_H(A)}\text{-}\mathsf{mod}} \quad \text{as categories,} \end{align} $$

for some $\mathbb {k}$ -algebra $R_H(A)$ which we call a reflective algebra. In Section 5.3.1, we construct a general isomorphism between ${}^C_B \mathsf {DH}(L)$ (from Section 5.2.1) and the category of modules of a crossed product algebra $B \rtimes _L (C^{*})^{\text {op}}$ . Next, we study the dual of the H-module coalgebra $\widehat {H}$ (from Section 5.2.2) in Section 5.3.2 and then define $R_H(A)$ as a crossed product algebra in Section 5.3.3.

5.3.1 Doi–Hopf modules and crossed products

In the setting of Section 5.2.1, consider the case when the left L-module coalgebra C is finite-dimensional. Then $C^{*}$ is a right L-module algebra with the L-action given by

(5.20) $$ \begin{align} \langle \xi \leftharpoonup \ell, c \rangle := \langle \xi, \ell \rightharpoonup c \rangle, \end{align} $$

for $\xi \in C^{*}, c \in C, \ell \in L$ . The same action makes $(C^{*})^{\mathrm {op}}$ a right $L^{\mathrm {cop}}$ -module algebra. Define the crossed product algebra (see [Doi92, Section 1])

$$\begin{align*}B \rtimes_L (C^{*})^{\mathrm{op}} := B \circledast (C^{*})^{\mathrm{op}}/ \left( \xi b - b_{[0]} (\xi \leftharpoonup b_{[-1]}),\;\; b \in B, \; \xi \in (C^{*})^{\mathrm{op}} \right), \end{align*}$$

where $\circledast $ denotes the free product of algebras. That is, for all $a,b \in B$ and $\xi , \zeta \in (C^{*})^{\mathrm {op}}$ , we get

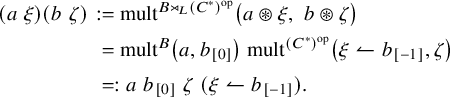(5.21) $$ \begin{align} \begin{array}{rl} (a \; \xi)(b \; \zeta) \; &:=\text{mult}^{B \rtimes_L (C^{*})^{\mathrm{op}}}\big(a \circledast \xi, \; b \circledast \zeta \big)\\[.4pc] & \; = \text{mult}^{B}\big(a, b_{[0]}\big) \; \text{mult}^{(C^{*})^{\mathrm{op}}}\big(\xi \leftharpoonup b_{[-1]}, \zeta\big)\\[.4pc] & \; =: a \; b_{[0]}\; \zeta \; (\xi \leftharpoonup b_{[-1]}). \end{array} \end{align} $$

Lemma 5.22. We have that $B \rtimes _L (C^{*})^{\mathrm {op}}$ is isomorphic to $B \otimes (C^{*})^{\mathrm {op}}$ as a $(B,(C^{*})^{\mathrm {op}})$ -bimodule.

Proof. Consider the tensor product $B \otimes (C^{*})^{\mathrm {op}}$ . It is straightforward to verify that the product (5.21) on it is associative, where $a, b \in B$ and $\xi , \zeta \in (C^{*})^{\mathrm {op}}$ . Therefore, $B \rtimes _L (C^{*})^{\mathrm {op}}$ is isomorphic to the space $B \otimes (C^{*})^{\mathrm {op}}$ with this product. This implies the statement of the lemma.

We now recall results relating Doi–Hopf modules to modules over the crossed product algebra.

Lemma 5.23. Let $\{c_d, \xi _d\}_d$ be a dual basis of C. Then, we have an isomorphism of categories:

$$\begin{align*}\Omega: C\text{-}\mathsf{comod} \overset{\sim}{\to} {{(C^{*})^{\mathrm{op}}}\text{-}\mathsf{mod}}, \end{align*}$$

given by the assignments, for $\xi \in C^{*}$ and $m \in M$ :

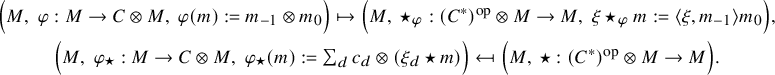
The following result is an analogue of [Doi92, Remark 1.3(b)] with our conventions.

Proposition 5.24. The functor below is an isomorphism of categories:

$$ \begin{align*} \Omega_{L;B,C}&\colon {}^C_B \mathsf{DH}(L) \to {{(B \rtimes_L (C^{*})^{\mathrm{op}})}\text{-}\mathsf{mod}}, \quad (M, \ast, \varphi) \mapsto (M, \star), \end{align*} $$

where $\star $ is defined by $\xi \star m:=\xi \star _\varphi m$ as given in Lemma 5.23, for $\xi \in C^{*}$ , and by $b\star m=b\ast m$ , for $b\in B$ and $m\in M$ .

Proof. Recall that $M \in {}^C_B \mathsf {DH}(L)$ is a left B-module via the action $\ast : B \otimes M \to M$ , and a left C-comodule via the action $\varphi : M \to C \otimes M$ , $m \mapsto m_{-1} \otimes m_0$ . By dualization, M is a left $(C^{*})^{\mathrm {op}}$ -module via Lemma 5.23. The two actions on M are compatible in the following way:

$$\begin{align*}\begin{array}{rll} \xi \star ( b \ast m) & \; = \; \langle \xi, (b \ast m)_{-1} \rangle (b \ast m)_{0} & \; \overset{\mathrm{(5.6)}}{=} \; \langle \xi, b_{[-1]} \rightharpoonup m_{-1} \rangle (b_{[0]} \ast m_0) \\[.4pc] &\; = \; b_{[0]} \ast \big( \langle \xi \leftharpoonup b_{[-1]}, m_{-1} \rangle m_0\big) & \; = \; b_{[0]} \ast \big( (\xi \leftharpoonup b_{[-1]}) \star m \big), \end{array} \end{align*}$$

for $\xi \in C^{*}, b \in B, m \in M$ . Therefore, the actions $\ast $ (resp., $\star $ ) of B and (resp., $(C^{*})^{\mathrm {op}}$ ) on M induce the stated action $\star $ of the crossed product $B \rtimes _L (C^{*})^{\mathrm {op}}$ on M; that is, $M \in {{(B \rtimes _L (C^{*})^{\mathrm {op}})}\text {-}\mathsf {mod}}$ . Clearly, the space of morphisms between $M, N \in {}^C_B \mathsf {DH}(L)$ coincides with the space of morphisms between M and N considered as $B \rtimes _L (C^{*})^{\mathrm {op}}$ -modules. This yields a functor

$$\begin{align*}\Omega_{L; B, C}: {}^C_B \mathsf{DH}(L) \to {{(B \rtimes_L (C^{*})^{\mathrm{op}})}\text{-}\mathsf{mod}}. \end{align*}$$

Moreover, this is an isomorphism of categories since ${{C}\text {-}\mathsf {comod}} \cong {{(C^{*})^{\mathrm {op}}}\text {-}\mathsf {mod}}$ by Lemma 5.23.

Remark 5.25. Note that, up to differences in conventions, the crossed product algebra $B \rtimes _L (C^{*})^{\mathrm {op}}$ is a smash product algebra as defined in [Tak80]; cf. [CMZ97, Section 3]. We also note that sometimes Doi-Hopf modules are referred to as Doi–Koppinen modules due to independent work of Koppinen in [Kop95].

5.3.2 The right H-module algebra $\widehat {H}^{*}$

Recall the left H-module coalgebra $\widehat {H}$ introduced in Section 5.2.2. Then, when H is finite-dimensional, the dual vector space $\widehat {H}^{*}$ has a canonical structure of a right H-module algebra, which is described in the next lemma.

Lemma 5.26. Assume that H is finite-dimensional. Then, given the left H-module coalgebra $\widehat {H}$ in Definition 5.7, we have the following statements.

1. (a) The induced algebra structure on $\widehat {H}^{*}$ is given as follows, for $\xi , \zeta \in \widehat {H}^{*}$ :

   $$ \begin{align*} \mathrm{mult}^{\widehat{H}^{*}}(\xi, \zeta) & \; = \; \textstyle \sum_{i,j} \big( t_i \twoheadrightarrow \xi \twoheadleftarrow S(t_j) \big) \big( s_i s_j \twoheadrightarrow \zeta \big). \end{align*} $$

2. (b) The induced right H-module algebra structure of $\widehat {H}^{*}$ is given as follows, for $\ell \in H$ , $\xi \in \widehat {H}^{*}$ :

   $$\begin{align*}\xi \leftharpoonup \ell = S^{-1}(\ell_{(1)}) \twoheadrightarrow \xi \twoheadleftarrow \ell_{(2)}. \end{align*}$$

Proof. Part (a) holds by the following computation:

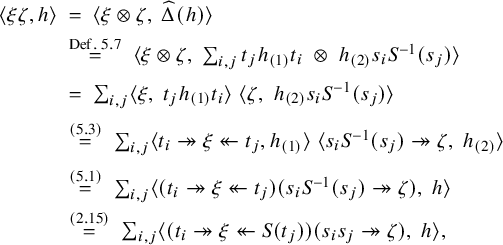$$ \begin{align*} \langle \xi \zeta, h \rangle \; &= \; \langle \xi \otimes \zeta, \; \widehat{\Delta}(h) \rangle \\ \; & \overset{\mathrm{Def.\;5.7}}{=} \; \langle \xi \otimes \zeta, \; \textstyle \sum_{i,j} t_j h_{(1)} t_i \; \otimes \; h_{(2)} s_i S^{-1}(s_j) \rangle \\[.2pc] \; &= \; \textstyle \sum_{i,j} \langle \xi, \; t_j h_{(1)} t_i \rangle \; \langle \zeta,\; h_{(2)} s_i S^{-1}(s_j) \rangle \\[.2pc] \; & \overset{\mathrm{(5.3)}}{=} \; \textstyle \sum_{i,j} \langle t_i \twoheadrightarrow \xi \twoheadleftarrow t_j, h_{(1)} \rangle \; \langle s_i S^{-1}(s_j) \twoheadrightarrow \zeta, \; h_{(2)} \rangle \\[.2pc] \; & \overset{\mathrm{(5.1)}}{=} \; \textstyle \sum_{i,j} \langle ( t_i \twoheadrightarrow \xi \twoheadleftarrow t_j ) ( s_i S^{-1}(s_j) \twoheadrightarrow \zeta), \; h \rangle \\ \; & \overset{\mathrm{(2.15)}}{=} \; \textstyle \sum_{i,j} \langle ( t_i \twoheadrightarrow \xi \twoheadleftarrow S(t_j) ) ( s_i s_j \twoheadrightarrow \zeta), \; h \rangle, \end{align*} $$

for all $\xi , \zeta \in \widehat {H}^{*}$ and $h \in \widehat {H}$ . Part (b) is proved by the next computation:

$$\begin{align*}\langle \xi \leftharpoonup \ell, h \rangle \; = \; \langle \xi, \ell \rightharpoonup h \rangle \; \overset{\mathrm{Def.\;5.7}}{=} \; \langle \xi, \;\ell_{(2)} h S^{-1}(\ell_{(1)}) \rangle \; \overset{\mathrm{(5.3)}}{=} \; \langle S^{-1}(\ell_{(1)}) \twoheadrightarrow \xi \twoheadleftarrow \ell_{(2)}, \; h \rangle, \end{align*}$$

for all $\xi \in \widehat {H}^{*}, h \in \widehat {H}, \ell \in H$ .

5.3.3 Definition of the reflective algebra

Now we present the main construction of this section.

Definition 5.27. For a finite-dimensional quasitriangular Hopf algebra H and a left H-comodule algebra A, define the reflective algebra of A with respect to H to be the crossed product algebra:

$$\begin{align*}R_H(A):= A \rtimes_H (\widehat{H}^{*})^{\mathrm{op}}. \end{align*}$$

The algebras A and $(\widehat {H}^{*})^{\mathrm {op}}$ are canonical subalgebras of the reflective algebra $R_H(A)$ . Moreover, by Lemma 5.22, $R_H(A)$ is isomorphic to $A \otimes (\widehat {H}^{*})^{\mathrm {op}}$ as an $(A, (\widehat {H}^{*})^{\mathrm {op}})$ -bimodule. Also, pertaining to Majid’s transmuted Hopf algebras discussed in Remark 5.8, we have that

$$\begin{align*}R_H(A) \; \cong \; A \rtimes_H (\widehat{H}^{\mathrm{cop}})^{*} \cong A \rtimes_H (H^{\mathrm{cop}})_{\mathrm{trm}}, \quad \text{as } \mathbb{k}\text{-algebras}. \end{align*}$$

Specializing the functor $\Omega _{L,B,C}$ from Proposition 5.24 to $L:=H, B:=A, C:=\widehat {H}^{*}$ gives the following corollary.

Corollary 5.28. For a finite-dimensional quasitriangular Hopf algebra H and a left H-comodule algebra A, the functor

$$\begin{align*}\Omega:= \Omega_{H; A, \widehat{H}^{*}} : {}_A^{\widehat{H}} \mathsf{DH}(H) \overset{\sim}{\longrightarrow} {{R_H(A)}\text{-}\mathsf{mod}}. \end{align*}$$

is an isomorphism of categories.

5.4 Properties of reflective algebras

In this part, we examine algebraic properties of reflective algebras and their categories of modules.

Proposition 5.29. For a finite-dimensional quasitriangular Hopf algebra H and a left H-comodule algebra A, we have the following facts about the reflective algebra $R_H(A)$ and its category of modules.

1. (a) If A is finite-dimensional, then $R_H(A)$ is finite-dimensional, and hence, $R_H(A)\text {-}\mathsf {fdmod}$ is a finite abelian category.

2. (b) If H is semisimple, and A is finite-dimensional and semisimple, then $R_H(A)$ is semisimple.

Proof. Part (a) follows from Lemma 5.22. Part (b) follows from Corollary 4.6(e).

Example 5.30. Consider the special cases of left H-comodule algebras A below. Take $A = \mathbb {k}$ to be the trivial left coideal subalgebra of H with $\delta (1_{\mathbb {k}}) = 1_H \otimes 1_{\mathbb {k}}$ . Then,

$$\begin{align*}R_H(\mathbb{k}) \cong (\widehat{H}^{*})^{\mathrm{op}}. \end{align*}$$

Here, ${{R_H(\mathbb {k})}\text {-}\mathsf {mod}}$ is abelian and finite. Moreover, $R_H(\mathbb {k})$ is semisimple when H is semisimple.

6 Modules over reflective algebras as braided module categories

We maintain the setting and notation of Section 5.1 here. The goal of this section is to upgrade the category isomorphisms of the previous section to isomorphisms of braided module categories. Namely in Sections 6.1 and 6.2, we establish how (5.4) and (5.19), respectively, can be extended to isomorphism of braided left ${\mathcal {C}}$ -module categories. We also obtain an H-comodule algebra structure and quantum K-matrix (i.e., quasitriangular structure) for the pertinent reflective algebra in Section 6.2. Next in Section 6.3, we display a universal property for the reflective algebra of the trivial H-comodule algebra $\mathbb {k}$ . Then in Section 6.4, we provide an explicit example of the results here for H being the Drinfeld double of a finite group.

Standing notation. Along with the notation of Section 5.1, we collect some additional notation introduced in the previous section.

• • ${}_{B}^{C} \mathsf {DH}(L)$ is the category of $(L,B,C)$ -Doi–Hopf modules from Section 5.2.1, with L a Hopf algebra, with objects $(M, \ast , \varphi )$ for $(M, \ast )$ a left B-module, and $(M, \varphi )$ a left C-module.

• • $\varphi (m):= m_{-1} \otimes m_0$ for $m \in M$ .

• • $\widehat {H}:=(\widehat {H}, \widehat {\Delta }, \widehat {\varepsilon }, \rightharpoonup )$ is the left H-module coalgebra from Definition 5.7; here, $\widehat {\Delta }(h):= h_{\widehat {(1)}} \otimes h_{\widehat {(2)}}$ .

• • When H is finite-dimensional, $\langle \hspace {0.02in}, \rangle $ is the algebra-coalgebra pairing between $\widehat {H}^{*}$ , $\widehat {H}$ . Here,

  (6.1) $$ \begin{align} \langle \xi \zeta, h \rangle = \langle \xi \otimes \zeta, \widehat{\Delta}(h) \rangle = \langle \xi, h_{\widehat{(1)}} \rangle \langle \zeta, h_{\widehat{(2)}} \rangle, \end{align} $$
  for $\xi , \zeta \in \widehat {H}^{*}$ , $h \in \widehat {H}$ .

• • $R_H(A)$ is the reflective algebra from Section 5.3.3; it is equal to $A \otimes H^{*}$ as a vector space.

6.1 Reflective centers are Doi–Hopf modules as braided module categories

By (5.4), we have the category isomorphism

$$\begin{align*}{\mathcal{E}}_{{{H}\text{-}\mathsf{mod}}}({{{A}\text{-}\mathsf{mod}}}) \; \cong \;{}_A^{\widehat{H}} \mathsf{DH}(H). \end{align*}$$

The goal of this subsection to describe explicitly the corresponding braided $({{H}\text {-}\mathsf {mod}})$ -module category structure of ${}_A^{\widehat {H}} \mathsf {DH}(H)$ . This will be akin to the isomorphism ${\mathcal {Z}}({{H}\text {-}\mathsf {mod}}) \; \overset {\otimes }{\cong } \; {{\vphantom {\mathsf {YD}}}^{H}_{H}{\mathsf {YD}}}$ of braided categories mentioned in (2.6).

Lemma 6.2. The following statements hold.

1. (a) We have that ${\mathcal {E}}_{{{H}\text {-}\mathsf {mod}}}({{{A}\text {-}\mathsf {mod}}})$ is a left module category over ${{H}\text {-}\mathsf {mod}}$ as follows:

   $$\begin{align*}\begin{array}{rl} \triangleright: {{H}\text{-}\mathsf{mod}} \;\times \;{\mathcal{E}}_{{{H}\text{-}\mathsf{mod}}}({{{A}\text{-}\mathsf{mod}}}) &\longrightarrow {\mathcal{E}}_{{{H}\text{-}\mathsf{mod}}}({{{A}\text{-}\mathsf{mod}}}) \\[.4pc] \left( (Y, \cdot), \; (M, \ast, e^M) \right) & \mapsto \left( Y \otimes M, \; \widetilde{\ast}, \; e^{Y \otimes M}\right), \end{array} \end{align*}$$

   for $a \; \widetilde {\ast } \; (y \otimes m) = (a_{[-1]} \cdot y) \otimes (a_{[0]} \ast m)$ with $a \in A$ , $y \in Y$ , $m \in M$ . Here, $e^{Y \otimes M}$ is given by

   (6.3) $$ \begin{align} e^{Y \otimes M}_X(x \otimes y \otimes m) = \textstyle \sum_{i,j,k} (t_k g_j s_i \cdot x) \otimes (s_k t_i \cdot y) \otimes (p_j \ast m), \end{align} $$
   for some element $\sum _j g_j\otimes p_j\in H\otimes A$ independent of choice of $Y,M$ .

2. (b) Further, the reflections $e^M$ equip ${\mathcal {E}}_{{{H}\text {-}\mathsf {mod}}}({{{A}\text {-}\mathsf {mod}}})$ with the structure of a braided module category over ${{H}\text {-}\mathsf {mod}}$ , where

   $$ \begin{align*}e^{{\mathcal{E}}}_{X,(M,e^M)} := e^M_X,\end{align*} $$
   for $X \in {{H}\text {-}\mathsf {mod}}$ and $(M,e^M) \in {\mathcal {E}}_{{{H}\text {-}\mathsf {mod}}}({{{A}\text {-}\mathsf {mod}}})$ . In particular, $e_X^M$ is a braiding if and only if $K:=\sum _j g_j \otimes p_j$ is a K-matrix for A.

Proof. Part (a) follows from Lemma 4.2. In particular, the formula for $\widetilde {\ast }$ is derived from Lemma 3.26(a). Note that there exists an element $\sum _j g_j\otimes p_j \in H \otimes A$ satisfying $e^M_X (x\otimes m)= \textstyle \sum _j (g_j\cdot x) \otimes (p_j\ast m)$ by Lemma 3.26(c). Then the formula for $e^{Y\otimes M}$ holds as follows:

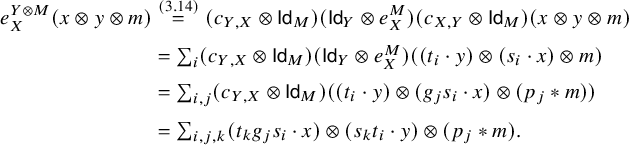$$ \begin{align*} e^{Y\otimes M}_X(x \otimes y \otimes m) & \overset{\mathrm{(3.14)}}{=} (c_{Y,X} \otimes \mathsf{Id}_M) (\mathsf{Id}_Y \otimes e_{X}^M) (c_{X,Y} \otimes \mathsf{Id}_M)(x \otimes y \otimes m)\\[.2pc] & = \textstyle \sum_i (c_{Y,X} \otimes \mathsf{Id}_M) (\mathsf{Id}_Y \otimes e_{X}^M) ((t_i \cdot y) \otimes (s_i \cdot x) \otimes m)\\[.2pc] & = \textstyle \sum_{i,j} (c_{Y,X} \otimes \mathsf{Id}_M) ((t_i \cdot y) \otimes (g_js_i \cdot x) \otimes (p_j \ast m))\\[.2pc] & = \textstyle \sum_{i,j,k} (t_kg_js_i \cdot x) \otimes (s_kt_i \cdot y) \otimes (p_j \ast m). \end{align*} $$

Part (b) holds by Proposition 4.3, and Lemma 3.26(b).

Next, we use the braided module category structure of ${\mathcal {E}}_{{{H}\text {-}\mathsf {mod}}}({{{A}\text {-}\mathsf {mod}}})$ in the lemma above to induce such a structure for ${}_A^{\widehat {H}} \mathsf {DH}(H)$ .

Proposition 6.4. We have that

$$\begin{align*}{\mathcal{E}}_{{{H}\text{-}\mathsf{mod}}}({{{A}\text{-}\mathsf{mod}}}) \; \overset{\mathrm{br.mod}}{\cong} \;{}_A^{\widehat{H}} \mathsf{DH}(H), \end{align*}$$

as braided left $({{{H}\text {-}\mathsf {mod}}})$ -module categories, where

1. (a) The left $({{{H}\text {-}\mathsf {mod}}})$ -module category structure on ${}_A^{\widehat {H}} \mathsf {DH}(H)$ is given by

   
   for $a\;\widetilde {\ast }\; (y \otimes m) = (a_{[-1]} \cdot y) \otimes (a_{[0]} \ast m)$ with $a \in A$ , $y \in Y$ , $m \in M$ , and for $\varphi (m):=m_{-1} \otimes m_0$ ,
   (6.5) $$ \begin{align} \widetilde{\varphi}(y \otimes m) = \textstyle \sum_{i,j} (t_j m_{-1} s_i) \otimes (s_j t_i \cdot y) \otimes m_{0}. \end{align} $$

2. (b) The braiding on ${}_A^{\widehat {H}} \mathsf {DH}(H)$ is given by

   $$ \begin{align*} e^{\mathsf{DH}}_{X,(M, \ast, \varphi)}(x \otimes m) := (m_{-1} \cdot x) \otimes m_0, \end{align*} $$
   for $X \in {{H}\text {-}\mathsf {mod}}$ and $(M, \ast , \varphi ) \in {}_A^{\widehat {H}} \mathsf {DH}(H)$ , with $x \in X, m \in M$ .

Proof. (a) By Proposition 3.21(a), the action is induced by the action $\triangleright $ from Lemma 6.2(a), the functor F from Proposition 5.10, and its inverse G from Proposition 5.16 as follows:

The formula for $\widetilde {\ast }$ then follows from Lemma 6.2. Moreover, the formula for $\widetilde {\varphi }$ follows from the computations below:

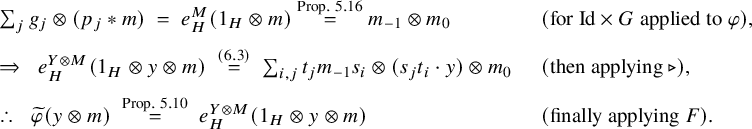$$\begin{align*}\begin{array}{ll} \textstyle \sum_j g_j \otimes (p_j \ast m) \; = \; e_H^M(1_H \otimes m) \overset{\mathrm{Prop.\;5.16}}{=} m_{-1} \otimes m_0 \; &\quad (\text{for } \mathrm{Id} \times G \text{ applied to } \varphi),\\[.6pc] \Rightarrow \; \; e_H^{Y \otimes M}(1_H \otimes y \otimes m) \; \overset{\mathrm{(6.3)}}{=} \; \textstyle \sum_{i,j} t_j m_{-1} s_i \otimes (s_j t_i \cdot y) \otimes m_0 \; &\quad (\text{then applying } \triangleright),\\[.6pc] \therefore \; \; \widetilde{\varphi}(y \otimes m) \; \overset{\mathrm{Prop.\;5.10}}{=} \; e_H^{Y \otimes M}(1_H \otimes y \otimes m) \; &\quad (\text{finally applying } F). \end{array} \end{align*}$$

(b) This follows from Proposition 3.21(b), Lemma 6.2(b) and computations as in part (a).

6.2 Reflective algebras as H-comodule algebras with quantum K-matrices

By (5.19), we have the category isomorphism

$$\begin{align*}{\mathcal{E}}_{{{H}\text{-}\mathsf{mod}}}({{{A}\text{-}\mathsf{mod}}}) \; \cong \; {{R_H(A)}\text{-}\mathsf{mod}}. \end{align*}$$

The goal of this subsection is to describe explicitly the corresponding braided ${{H}\text {-}\mathsf {mod}}$ module category structure of ${{R_H(A)}\text {-}\mathsf {mod}}$ . This will be akin to the isomorphism of braided categories, ${\mathcal {Z}}({{H}\text {-}\mathsf {mod}}) \; \overset {\otimes }{\cong } \; {{{\operatorname {Drin}}(H)}\text {-}\mathsf {mod}}$ mentioned in (2.6).

Theorem 6.6. For a finite-dimensional quasitriangular Hopf algebra H and a left H-comodule algebra A, we have that

(6.7) $$ \begin{align} {\mathcal{E}}_{{{H}\text{-}\mathsf{mod}}}({{{A}\text{-}\mathsf{mod}}}) \; \overset{\mathrm{br.mod}}{\cong} \; {{R_H(A)}\text{-}\mathsf{mod}}, \end{align} $$

as braided left $({{{H}\text {-}\mathsf {mod}}})$ -module categories, where

1. (a) The left $({{{H}\text {-}\mathsf {mod}}})$ -module category structure on ${{R_H(A)}\text {-}\mathsf {mod}}$ is given by

   
   for $a \; \widetilde {\ast } \; (y \otimes m) = (a_{[-1]} \cdot y) \otimes (a_{[0]} \ast m)$ with $a \in A$ , $y \in Y$ , $m \in M$ . Also for $\xi \in (\widehat {H}^{*})^{\mathrm {op}}$ :
   (6.8) $$ \begin{align} \xi \; \widetilde{\star}\; (y \otimes m) = \textstyle \sum_{i,j,d} \langle \xi,\; t_j h_d s_i \rangle (s_j t_i \cdot y) \otimes (\xi_d \star m). \end{align} $$

   Here, $\{h_d, \; \xi _d\}_d$ is a dual basis of H.

2. (a) The braiding on ${{R_H(A)}\text {-}\mathsf {mod}}$ is given by

   $$ \begin{align*}e^{R_H}_{X,(M, \star)}(x \otimes m) := \textstyle \sum_d (h_d \cdot x) \otimes (\xi_d \star m),\end{align*} $$
   for $X \in {{H}\text {-}\mathsf {mod}}$ and $(M, \star ) \in {{R_H(A)}\text {-}\mathsf {mod}}$ , with $x \in X, m \in M$ .

Proof. The braided isomorphism between ${\mathcal {E}}_{{{H}\text {-}\mathsf {mod}}}({{{A}\text {-}\mathsf {mod}}})$ and ${}_A^{\widehat {H}} \mathsf {DH}(H)$ follows from Proposition 6.4. To establish the braided isomorphism between ${}_A^{\widehat {H}} \mathsf {DH}(H)$ and ${{R_H(A)}\text {-}\mathsf {mod}}$ , see the work below.

(a) According to Proposition 3.21(a), the action is induced by the action from Proposition 6.4(a), the functors $\Omega $ and its inverse from Corollary 5.28 as such:

The formula for $\widetilde {\ast }$ follows from Lemma 6.2. The formula for $\widetilde {\star }:= \widetilde {\star }_{\widetilde {\varphi }_\star }$ is from the computations below:

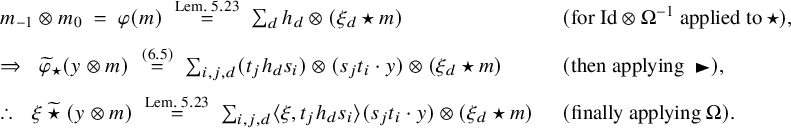
(b) This follows from Propositions 3.21(b) and 6.4(b), and computations as in part (a).

Now we obtain a quasitriangular structure for the reflective algebra $R_H(A)$ .

Corollary 6.9. For a finite-dimensional quasitriangular Hopf algebra H and a left H-comodule algebra A, we have the statements below about the reflective algebra $R_H(A)$ .

1. (a) $R_H(A)$ is a left H-comodule algebra with left H-coaction $\delta _{\mathrm {ref}}$ on $R_H(A)$ given by

   $$ \begin{align*} \delta_{\mathrm{ref}}(a) &:= a_{[-1]} \otimes a_{[0]},\\[.3pc] \delta_{\mathrm{ref}}(\xi) &:= \textstyle \sum_{i,j,d} \langle \xi,\; t_j h_d s_i \rangle s_j t_i \; \otimes \; \xi_d \quad (=: \xi_{[-1]} \otimes \xi_{[0]}),\\[.3pc] \delta_{\mathrm{ref}}(a \; \xi)&:= \delta_{\mathrm{ref}}(a)\; \delta_{\mathrm{ref}}(\xi) \quad (=: a_{[-1]} \xi_{[-1]} \otimes a_{[0]} \xi_{[0]}), \end{align*} $$
   for $a \in A$ and $\xi \in (\widehat {H}^{*})^{\mathrm {op}}$ . Here, recall that $\sum _i s_i \otimes t_i$ is the R-matrix of H and that $\{h_d, \xi _d\}_d$ is a dual basis of H.

2. (b) $R_H(A)$ is quasitriangular (as an H-comodule algebra) with K-matrix

   (6.10) $$ \begin{align} K_{\mathrm{ref}}(A) := \textstyle \sum_d h_d \otimes \xi_d \; \in H \otimes (\widehat{H}^{*})^{\mathrm{op}} \; \subset H \otimes R_H(A). \end{align} $$

Proof. (a) Since (6.7) is an isomorphism of left ${{H}\text {-}\mathsf {mod}}$ -module categories,

(6.11) $$ \begin{align} r \cdot (x \otimes m) = \delta_{\mathrm{ref}}(r) (x \otimes m), \end{align} $$

for all $r \in R_H(A)$ , $x \in X$ , $m \in M$ for some $\delta _{\mathrm {ref}} : R_H(A) \to H \otimes R_H(A)$ comodule algebra map. The formulas for $\delta _{\mathrm {ref}}(a)$ and $\delta _{\mathrm {ref}}(\xi )$ follow from the formulas for $\widetilde {\ast }$ and $\widetilde {\star }$ , respectively, in Theorem 6.6(a), applied to the left regular modules $X=H, M=A$ and the elements $x=1_H, m=1_A$ .

(b) This follows from Lemma 3.26(b) and Theorem 6.6(b). In the arXiv version 1 of this article, it is shown directly that $\delta _{\mathrm {ref}}$ defines an H-comodule algebra structure and that the axioms (3.23)-(3.25) hold for $K_{\mathrm {ref}}(A)$ .

Example 6.12. Corollary 6.9 implies that the isomorphism $R_H(\mathbb {k}) \cong (\widehat {H}^{*})^{\mathrm {op}}$ from Example 5.30 is an isomorphism of H-comodule algebras.

Example 6.13. When H is cocommutative, it is quasitriangular with $R = 1_H \otimes 1_H$ . Here, $R_H(A)$ is a left H-comodule algebra, where for $a \in A$ and $\xi \in (\widehat {H}^{*})^{\mathrm {op}}$ , we have $\delta _{\mathrm {ref}}(a) = a_{[-1]} \otimes a_{[0]}$ (identified with $a_{[-1]} \otimes (a_{[0]} \otimes \widehat {\varepsilon })$ in $H \otimes R_H(A)$ ) and

$$\begin{align*}\delta_{\mathrm{ref}}(\xi) = \textstyle \sum_{i,j,d} \langle \xi, h_d \rangle \otimes \; \xi_d \overset{\mathrm{(5.1)}}{=} \xi \qquad (\text{identified with } 1_H \otimes (1_A \otimes \xi) \text{ in } H \otimes R_H(A)). \end{align*}$$

6.3 Universality of the reflective algebra $R_H(\mathbb {k})$

In this part, we show that the reflective algebra $R_H(\mathbb {k})$ arises as an initial object of the category of quasitriangular left H-comodule algebras. Here, we assume that H is finite-dimensional.

Definition 6.14. Let ${}^H \mathsf {QT}$ be the category of quasitriangular left H-comodule algebras. Namely,

1. (a) Objects are pairs, $(Q, K)$ , where Q is a left H-comodule algebra, and $K:=K(Q) \in H \otimes Q$ is a quantum K-matrix for Q, and

2. (b) A morphism from $(Q_1,K_1)$ to $(Q_2,K_2)$ is a linear map $\phi : Q_1 \to Q_2$ that is both a left H-comodule morphism and an algebra morphism, such that $K_2 = (\mathsf {Id}_H \otimes \phi )(K_1)$ .

Indeed, if $(Q,K) \in {}^H \mathsf {QT}$ , then the identity morphism $\mathsf {Id}_{(Q,K)}$ is equal to $\mathsf {Id}_Q$ because $\mathsf {Id}_Q$ is a left H-comodule algebra morphism and $K = (\mathsf {Id}_H \otimes \mathsf {Id}_Q)(K)$ . Also if we have morphisms $\phi _1:(Q_1,K_1) \to (Q_2,K_2)$ and $\phi _2: (Q_2,K_2) \to (Q_3,K_3)$ in ${}^H \mathsf {QT}$ , then $\phi _2 \phi _1: (Q_1,K_1) \to (Q_3,K_3)$ is in ${}^H \mathsf {QT}$ since it is a left H-comodule algebra morphism and $(\mathsf {Id}_H \otimes \phi _2 \phi _1)(K_1) = (\mathsf {Id}_H \otimes \phi _2)(K_2) = K_3$ .

Examples of objects of ${}^H \mathsf {QT}$ include the pairs $(R_H(A), K_{\mathrm {ref}}(A))$ , for the reflective algebra $R_H(A)$ of A from Section 5.3.3, with K-matrix $K_{\mathrm {ref}}(A)$ given in (6.10).

Now the main result of this section is given below.

Theorem 6.15. When H is a finite-dimensional quasitriangular Hopf algebra over $\mathbb {k}$ , we have that $(R_H(\mathbb {k}), K_{\mathrm {ref}}(\mathbb {k}))$ is an initial object of ${}^H \mathsf {QT}$ .

Proof. For an arbitrary object $(Q, K) \in {}^H \mathsf {QT}$ , our task is to produce a unique morphism

$$ \begin{align*}\kappa:= \kappa_{(Q,K)}: (R_H(\mathbb{k}), K_{\mathrm{ref}}(\mathbb{k})) \to (Q, K)\end{align*} $$

in ${}^H \mathsf {QT}$ . Toward this, recall that $R_H(\mathbb {k}) \cong (\widehat {H}^{*})^{\mathrm {op}}$ as left H-comodule algebras [Example 6.12]. So, $R_H(\mathbb {k}) \cong H^{*}$ as vector spaces [Definition 5.7]. Now we use the element $K:= \sum _i g_i \otimes p_i \in H \otimes Q$ to yield a linear map:

(6.16) $$ \begin{align} \kappa:= \kappa_{(Q,K)}: R_H(\mathbb{k}) \cong H^{*} \to Q, \quad \xi \mapsto \textstyle \sum_i \langle \xi, g_i \rangle \; p_i. \end{align} $$

It now remains to verify the following conditions for the linear map in (6.16).

1. (i) It is a left H-comodule morphism.

2. (ii) It is an algebra morphism;

3. (iii) $K = (\mathsf {Id}_H \otimes \kappa )(K_{\mathrm {ref}}(\mathbb {k}))$ .

4. (iv) Uniqueness: If $\kappa ': H^{*} \to Q$ is a linear map satisfying (i)–(iii), then $\kappa ' = \kappa $ .

Toward (i), we have that the left H-comodule structure on $R_H(\mathbb {k}) \cong (\widehat {H}^{*})^{\mathrm {op}}$ is given by

$$\begin{align*}\delta_{\mathrm{ref}}(\xi) = \textstyle \sum_{i,j,d} \langle \xi,\; t_j h_d s_i \rangle s_j t_i \; \otimes \; \xi_d \end{align*}$$

for $\xi \in (\widehat {H}^{*})^{\mathrm {op}}$ by Corollary 6.9(a). Here, $\sum _i s_i \otimes t_i$ is the R-matrix of H, and $\{h_d, \xi _d\}_d$ is a dual basis of H. Now (6.16) is a left H-comodule morphism as shown below:

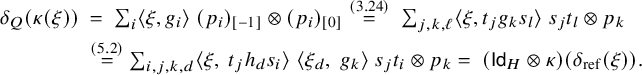$$ \begin{align*} \delta_Q(\kappa(\xi)) \; &= \; \textstyle \sum_i \langle \xi, g_i \rangle \; (p_i)_{[-1]} \otimes (p_i)_{[0]} \overset{\mathrm{(3.24)}}{=} \; \textstyle \sum_{j,k,\ell} \langle \xi, t_j g_k s_l \rangle \; s_j t_l \otimes p_k \\ \; & \overset{\mathrm{(5.2)}}{=} \textstyle \sum_{i,j,k,d} \langle \xi,\; t_j h_d s_i \rangle\; \langle \xi_d,\; g_k \rangle \; s_j t_i \otimes p_k = \; (\mathsf{Id}_H \otimes \kappa) ( \delta _{\mathrm{ref}}(\xi)). \end{align*} $$

To verify (ii), take $\xi , \zeta \in (\widehat {H}^{*})^{\mathrm {op}}$ , and consider the computation below:

$$ \begin{align*} \kappa(\xi \zeta) \; &=\textstyle \sum_{i} \langle \xi \zeta, g_i \rangle \;p_i \\[.2pc] \; & \overset{\mathrm{(6.1)}, \; \mathrm{Def.~5.7}}{=} \textstyle \sum_{i,j',k'} \langle \zeta, t_{k'} (g_i)_{(1)} t_{j'} \rangle \; \langle \xi, \; (g_i)_{(2)} s_{j'} S^{-1}(s_{k'}) \rangle \;p_i\\ \; &\overset{\mathrm{(3.23)}}{=} \textstyle \sum_{j,k,l,m,j',k'} \langle \zeta, \; t_{k'} t_k g_l t^m t_{j'} \rangle \; \langle \xi, \; g_j s_k s^m s_{j'} S^{-1}(s_{k'}) \rangle \;p_j p_l \\[.2pc] \; &= \textstyle \sum_{j,k,l,k'} \langle \zeta, \; t_{k'} t_k g_l \rangle \; \langle \xi, \; g_j S^{-1}(s_{k'} S(s_k)) \rangle \;p_j p_l\\ \; & \overset{\mathrm{(2.15)}}{=} \textstyle \sum_{j,l} \langle \zeta, g_l \rangle \; \langle \xi, g_j) \rangle \;p_j p_l\\[.2pc] \; &= \kappa(\xi) \kappa(\zeta). \end{align*} $$

Next, we establish (iii) as follows:

$$ \begin{align*} (\mathsf{Id}_H \otimes \kappa)(K_{\mathrm{ref}}(\mathbb{k})) \; \overset{\mathrm{(6.10)}}{=} \; \textstyle \sum_{i,d} \langle \xi_d, g_i \rangle \; h_d \otimes p_i \; \overset{\mathrm{(5.2)}}{=} \; \textstyle \sum_{i} g_i \otimes p_i = K. \end{align*} $$

Finally, we verify (iv). If $K = \textstyle (\mathsf {Id}_H \otimes \kappa ')(K_{\mathrm {ref}}(\mathbb {k}))$ , then $\textstyle \sum _i g_i \otimes p_i = \sum _d h_d \otimes \kappa '(\xi _d)$ . Applying $\langle \xi _d, - \rangle $ to the first factor yields $\kappa '(\xi _d) = \textstyle \sum _i \langle \xi _d, g_i \rangle \; p_i$ , for all d. Since $\{\xi _d\}_d$ is a basis for $H^{*}$ , we get that $\kappa '(\xi ) = \textstyle \sum _i \langle \xi , g_i \rangle \; p_i$ for all $\xi \in H^{*}$ , as desired.

One may compare the result above to [Rad94, Theorem 1] on ${\operatorname {Drin}}(H)$ realized as a universal quasitriangular envelope of H. Moreover, the verification of (ii) in the proof above compares to [BZBJ18, Theorem 4.9] with the distinction that we work with H-comodule algebras A. Next, consider the following example.

Example 6.17. For the object $(R_H(A), K_{\mathrm {ref}}(A)) \in {}^H \mathsf {QT}$ , we obtain via Lemma 5.22 a canonical algebra embedding

$$\begin{align*}\iota_A : R_H(\mathbb{k}) \cong (\widehat{H}^{*})^{\mathrm{op}} \hookrightarrow R_H(A). \end{align*}$$

By Corollary 6.9(a), this is an embedding of H-comodule algebras, and from (6.10), we have $\iota _A(K_{\mathrm {ref}}(\mathbb {k})) = K_{\mathrm {ref}}(A). $ Therefore, $\iota _A$ is the unique homomorphism $\kappa _{(R_H(A), K_{\mathrm {ref}}(A))}$ from the proof of Theorem 6.15.

6.4 Example for the Drinfeld double of a finite group

In this subsection, we illustrate how our results apply to the case when H is the Drinfeld double of a finite group.

Take G to be a finite group. Let $\mathbb {k} G$ be the group algebra on G, and consider its Hopf dual, $(\mathbb {k} G)^{*}$ , the algebra of functions on G. Denote by $\{x\}_{x \in G}$ and $\{ \delta _x \}_{x \in G}$ the standard $\mathbb {k}$ -bases of $\mathbb {k} G$ and $(\mathbb {k} G)^{*}$ , respectively. Also, take $\delta _{g,h}$ to be the Kronecker delta function, for $g,h \in G$ .

The Drinfeld double ${\operatorname {Drin}}(G) := {\operatorname {Drin}}(\mathbb {k} G)$ contains $\mathbb {k} G$ and $((\mathbb {k} G)^{*})^{\mathrm {op}}$ as Hopf subalgebras, and is $(\mathbb {k} G)^{*} \otimes \mathbb {k} G$ as a $\mathbb {k}$ -coalgebra. The $\mathbb {k}$ -basis of ${\operatorname {Drin}}(G)$ is given by $\{ \delta _x y \}_{x, y \in G}$ , with product

$$\begin{align*}\big(\delta_x y \big) \big( \delta_{x'} y' \big) = \delta_{x, y x' y^{-1}} \; \delta_x \; y y', \end{align*}$$

for $x, x', y, y' \in G$ . The quantum R-matrix of ${\operatorname {Drin}}(G)$ is

(6.18) $$ \begin{align} R = \textstyle \sum_{g \in G} \delta_g \otimes g. \end{align} $$

Also, as $\mathbb {k}$ -algebras, $({\operatorname {Drin}}(G))^{*}$ is isomorphic to $\mathbb {k} G \otimes (\mathbb {k} G)^{*}$ , with $\mathbb {k}$ -basis $\{x \delta _y \}_{x, y \in G}$ and product

$$\begin{align*}(x \delta_y) (x' \delta_{y'}) = \delta_{y,y'} \; x x' \; \delta_y. \end{align*}$$

Now we illustrate Corollary 6.9 (and Theorem 6.15) for the left ${\operatorname {Drin}}(G)$ -comodule algebra $\mathbb {k}$ .

Proposition 6.19. Retain the notation above, and take $H:={\operatorname {Drin}}(G)$ . Then we obtain that the reflection algebra $R_H(\mathbb {k}) \cong (\widehat {H}^{*})^{\mathrm {op}}$ is a quasitriangular left H-comodule algebra as follows:

1. (a) Its algebra structure is given as follows, for all $x, y, x', y' \in G$ :

   $$\begin{align*}\big( x \delta_y \big) \big( x' \delta_{y'} \big)= \delta_{y', y^{-1} x^{-1} y x y} \; y^{-1} x y x' y^{-1} x^{-1} y x \; \delta_y. \end{align*}$$

2. (b) Its left H-comodule structure is given as follows, for all $x, y \in G$ :

   $$\begin{align*}\textstyle \delta_{\mathrm{ref}} (x \delta_y) = \textstyle \sum_{g \in G} \delta_g\; y^{-1} x y \; \otimes\; g^{-1} x g \; \delta_{g^{-1} y} \quad \in H \otimes H^{*} \subset H \otimes R_H(A). \end{align*}$$

3. (c) Its quantum K-matrix is given by $K=\sum _{g,h \in G} \delta _g h \otimes g \delta _h \in H \otimes R_H(A)$ .

Proof. (a) To start, we compute

$$\begin{align*}\langle g \twoheadrightarrow x \delta_y \twoheadleftarrow h, \delta_u v \rangle = \langle x \delta_y, h \delta_u v g \rangle = \langle x \delta_y, \delta_{h u h^{-1}} h v g \rangle = \delta_{u, h^{-1} x h} \; \delta_{v, h^{-1} y g^{-1}} \end{align*}$$

for all $x,y,g,h,u,v \in G$ . Thus, for $x,y, g, h \in G$ ,

$$\begin{align*}g \twoheadrightarrow x \delta_y \twoheadleftarrow h = h^{-1} x h \; \delta_{h^{-1} y g^{-1}}. \end{align*}$$

Analogously, one obtains, for $x,y, g \in G$ ,

$$\begin{align*}\delta_g \twoheadrightarrow x \delta_y = \delta_{g, y^{-1} x y} \; x \delta_y. \end{align*}$$

Lemma 5.26(a) and (6.18) now imply that the product structure of $(\widehat {H}^{*})^{\mathrm {op}}$ is given by

$$ \begin{align*} (x \delta_y) (x' \delta_{y'}) &= \textstyle \sum_{g, h \in G} (g \twoheadrightarrow x' \delta_{y'} \twoheadleftarrow h^{-1} ) ( \delta_g \delta_{h} \twoheadrightarrow x \delta_y ) = \textstyle \sum_{g \in G} (g \twoheadrightarrow x' \delta_{y'} \twoheadleftarrow g^{-1} ) ( \delta_g \twoheadrightarrow x \delta_y ) \\[.2pc] &= \textstyle \sum_{g \in G} \delta_{g, y^{-1} x y}\; \delta_{g y' g^{-1},y} \; g x' g^{-1} x \;\delta_y, \end{align*} $$

which yields the statement in part (a) after simplifying the right-hand side.

(b) Note that $\{\delta _k k', k \delta _{k'} \}_{k,k' \in G}$ is a dual basis of H. Corollary 6.9(a) and (6.18) imply

$$ \begin{align*} \delta_{\mathrm{ref}} (x \delta_y) &= \textstyle \sum_{g,h,k,k' \in G} \; \langle x \delta_y,\; g \delta_k k' \delta_h \rangle \; \delta_g h \otimes k \delta_{k'} \\[.2pc] &= \textstyle \sum_{g,h,k,k' \in G}\; \langle x \delta_y, \; \delta_{g k g^{-1}} \; \delta_{g k' h (k')^{-1} g^{-1}}\; g k' \rangle \; \delta_g h \otimes k \delta_{k'} \\[.2pc] &= \textstyle \sum_{g,h,k,k' \in G} \; \delta_{x, g k g^{-1}}\; \delta_{x, g k' h (k')^{-1} g^{-1}}\; \delta_{y, gk'} \; \delta_g h \otimes k \delta_{k'} \\[.2pc] &= \textstyle \sum_{g \in G} \delta_g\; y^{-1} x y \; \otimes\; g^{-1} x g \; \delta_{g^{-1} y}, \end{align*} $$

where on the fourth line, the delta functions imply $k' = g^{-1} y, k = g^{-1} x g$ and $h = y^{-1} x y$ . The statement in part (b) is then obtained after simplifying the right-hand side.

Part (c) follows directly from Corollary 6.9(b).

6.5 Reflective algebras as comodule algebras over Drinfeld doubles

We return to the general standing notation from Section 5.1.

The action of ${\mathcal {Z}}({{H}\text {-}\mathsf {mod}})$ on ${\mathcal {E}}_{{{H}\text {-}\mathsf {mod}}}({{A}\text {-}\mathsf {mod}})$ from Corollary 4.6(a) can be explicitly computed. Based on this, one obtains explicit actions of the category of Yetter–Drinfeld modules ${{\vphantom {\mathsf {YD}}}^{H}_{H}{\mathsf {YD}}}$ on the category of Doi–Hopf modules ${}_A^{\widehat {H}} \mathsf {DH}(H)$ and, when H is a finite-dimensional Hopf algebra, of ${{{\operatorname {Drin}}(H)}\text {-}\mathsf {mod}}$ on ${{R_H(A)}\text {-}\mathsf {mod}}$ . The latter result equips $R_H(A)$ with a left ${\operatorname {Drin}}(H)$ -comodule algebra structure. These results and their detailed proofs appear in Section 7 of the arXiv version 1 of this article. Here, we only record the last result:

Proposition 6.20. If H is a finite-dimensional Hopf algebra and A a left H-comodule algebra, then the reflective algebra $R_H(A)$ is a left ${\operatorname {Drin}}(H)$ -comodule algebra as follows:

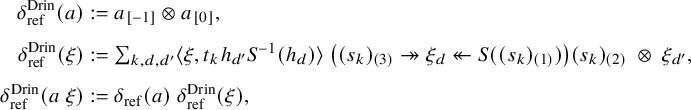$$ \begin{align*} \delta^{\mathrm{{\tiny Drin}}}_{\mathrm{ref}}(a) &:= a_{[-1]} \otimes a_{[0]},\\[.3pc] \delta^{\mathrm{{\tiny Drin}}}_{\mathrm{ref}}(\xi) &:= \textstyle \sum_{k,d,d'} \langle \xi, t_k h_{d'} S^{-1}(h_d) \rangle \; \left((s_k)_{(3)} \twoheadrightarrow \xi_d \twoheadleftarrow S((s_k)_{(1)})\right)(s_k)_{(2)} \; \otimes \;\xi_{d'},\\[.3pc] \delta^{\mathrm{{\tiny Drin}}}_{\mathrm{ref}}(a \; \xi)&:= \delta_{\mathrm{ref}}(a)\; \delta^{\mathrm{{\tiny Drin}}}_{\mathrm{ref}}(\xi), \end{align*} $$

for $a \in A$ and $\xi \in (\widehat {H}^{*})^{\mathrm {op}}$ . Here, recall that $\sum _k s_k \otimes t_k$ is the R-matrix of H, and that $\{h_d, \xi _d\}_d$ , $\{h_{d'}, \xi _{d'}\}_{d'}$ are dual bases of H.

Example 6.21. Let us continue Example 6.13 when H is cocommutative with $R = 1_H \otimes 1_H$ . Here, $R_H(A)$ is a left ${\operatorname {Drin}}(H)$ -comodule algebra, where for $a \in A$ and $\xi \in (\widehat {H}^{*})^{\mathrm {op}}$ , we have $\delta ^{\mathrm {{\tiny Drin}}}_{\mathrm {ref}}(a) = a_{[-1]} \otimes a_{[0]}$ (identified with $(\varepsilon \otimes a_{[-1]}) \otimes (a_{[0]} \otimes \widehat {\varepsilon })$ in ${\operatorname {Drin}}(H) \otimes R_H(A)$ ) and

$$\begin{align*}\delta^{\mathrm{{\tiny Drin}}}_{\mathrm{ref}}(\xi) = \textstyle \sum_{d,d'} \langle \xi, h_{d'} S^{-1}(h_d) \rangle \left(1_H \twoheadrightarrow \xi_d \twoheadleftarrow 1_H\right) \; \otimes \;\xi_{d'} = \textstyle \sum_{d,d'} \langle \xi, h_{d'} S^{-1}(h_d) \rangle \; \xi_d \; \otimes \;\xi_{d'}.\end{align*}$$

Here, $\xi _d \otimes \xi _{d'}$ is identified with $(\xi _d \otimes 1_H) \otimes (1_A \otimes \xi _{d'})$ in ${\operatorname {Drin}}(H) \otimes R_H(A)$ .