Hostname: page-component-7f64f4797f-d87pz Total loading time: 0 Render date: 2025-11-03T23:25:56.479Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal linear sofic approximations of countable groups

Part of: Stochastic processes Structure and classification of infinite or finite groups Probability theory on algebraic and topological structures

Published online by Cambridge University Press:  24 January 2025

Keivan Mallahi-Karai Open the ORCID record for Keivan Mallahi-Karai [Opens in a new window]  and
Maryam Mohammadi Yekta
Keivan Mallahi-Karai*
Affiliation:
Constructor University, Bremen, Germany
Maryam Mohammadi Yekta
Affiliation:
University of Waterloo, Ontario, Canada
*
Corresponding author: Keivan Mallahi-Karai; Email: kmallahikarai@constructor.university
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $G$ be a group. The notion of linear sofic approximations of $G$ over an arbitrary field 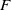$F$ was introduced and systematically studied by Arzhantseva and Păunescu [3]. Inspired by one of the results of [3], we introduce and study the invariant 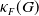$\kappa _F(G)$ that captures the quality of linear sofic approximations of $G$ over 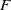$F$. In this work, we show that when 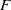$F$ has characteristic zero and $G$ is linear sofic over 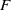$F$, then 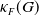$\kappa _F(G)$ takes values in the interval 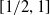$[1/2,1]$ and 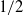$1/2$ cannot be replaced by any larger value. Further, we show that under the same conditions, 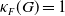$\kappa _F(G)=1$ when $G$ is torsion-free. These results answer a question posed by Arzhantseva and Păunescu [3] for fields of characteristic zero. One of the new ingredients of our proofs is an effective non-concentration estimates for random walks on finitely generated abelian groups, which may be of independent interest.

Keywords

linear sofic groupsmetric approximationssofic groups

MSC classification

Primary: 60B15: Probability measures on groups or semigroups, Fourier transforms, factorization 20E26: Residual properties and generalizations; residually finite groups
Secondary: 60G50: Sums of independent random variables; random walks

Information

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 67 , Issue 2 , May 2025 , pp. 245 - 268
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Arzhantseva, G. and Cherix, P. A., Quantifying metric approximations of discrete groups, Ann. Fac. Sci. Toulouse Math, Série 6, 33(3) (2024), 831–877.CrossRefGoogle Scholar
Arzhantseva, G. and Paunescu, L., Almost commuting permutations are near commuting permutations, J. Funct. Anal. 269(3) (2015), 745–757. MR 3350728.CrossRefGoogle Scholar
Arzhantseva, G. and Păunescu, L., Linear sofic groups and algebras, Trans. Amer. Math. Soc. 369(4) ( 2017), 2285–2310.Google Scholar
Becker, O. and Lubotzky, A., Group stability and property (T), J. Funct. Anal. 278(1) (2020), 108298. MR 4027744.CrossRefGoogle Scholar
Becker, O., Lubotzky, A. and Thom, A., Stability and invariant random subgroups, Duke Math. J. 168(12) (2019), 2207–2234. MR 3999445.Google Scholar
De Chiffre, M., Glebsky, L., Lubotzky, A. and Thom, A., Stability, cohomology vanishing, and nonapproximable groups, Forum Math. Sigma. 8(e18) (2020), 37. MR 4080477.Google Scholar
Elek, G. and Grabowski, Ł., Almost commuting matrices with respect to the rank metric, Groups Geom. Dyn. 15(3) (2021), 1059–1083. MR 4322021.CrossRefGoogle Scholar
Elek, G. and Szabó, E., Hyperlinearity, essentially free actions and L 2-invariants, the sofic property, Math. Ann. 332(2) (2005), 421–441. MR 2178069.Google Scholar
Esseen, C. G., On the Kolmogorov-Rogozin inequality for the concentration function, Z. Wahrscheinlichkeitstheorie Und Verw. Gebiete 5(3) (1966), 210–216. MR 205297.CrossRefGoogle Scholar
Glebsky, L. and Rivera, L. M., Almost solutions of equations in permutations, Taiwanese J. Math. 13(2A) (2009), 493–500. MR 2500002.CrossRefGoogle Scholar
Gromov, M., Endomorphisms of symbolic algebraic varieties, J. Eur. Math. Soc. (JEMS) 1(2) (1999), 109–197. MR 1694588.CrossRefGoogle Scholar
Iima, K. and Iwamatsu, R., On the Jordan decomposition of tensored matrices of Jordan canonical forms, Math. J. Okayama Univ. 51 (2009), 133–148. MR 2482411.Google Scholar
Kolmogorov, A., Sur les propriétés des fonctions de concentrations de M. P. Lévy. Ann. Inst. H. Poincaré 16 (1958), 27–34. MR 101545.Google Scholar
Luong, B, Fourier analysis on finite abelian groups, Applied and Numerical Harmonic Analysis (Birkhäuser Boston, Ltd, Boston, MA, 2009). MR 2537697.Google Scholar
Maples, K., Singularity of random matrices over finite fields, 2010. https://arxiv.org/abs/1012.2372 Google Scholar
Matousek, J., Understanding and using linear programming (Springer, Berlin, 2007).Google Scholar
Nakaoka, M., Finite groups which act freely on spheres, Osaka Math. J. 11 (1974), 323–330. MR 356108.Google Scholar
Nguyen, H. H. and Wood, M. M., Random integral matrices: universality of surjectivity and the cokernel, Invent. Math. 228 (1) (2022), 1–76.Google Scholar
Petrov, V. V., Ergebnisse der Mathematik und ihrer Grenzgebiete, Sums of independent random variables (Springer-Verlag, New York-Heidelberg, 1975). Band 82, Translated from the Russian by A. A. Brown. MR 0388499Google Scholar
Rogozin, B. A., An estimate of the concentration functions, Teor. Verojatnost. i Primenen 6 (1961), 103–105. MR 0131893.Google Scholar
Rădulescu, F., The von Neumann algebra of the non-residually finite Baumslag group embeds into, Hot topics in operator theory, Theta Ser. Adv. Math, vol. 9 (Theta, Bucharest, 2008), 173–185. MR 2436761.Google Scholar
Tao, T. and Van, V., Additive combinatorics (Cambridge University Press, Cambridge, 2006)CrossRefGoogle Scholar
Weiss, B., Sofic groups and dynamical systems, Ergodic theory and harmonic analysis, 62 (2000), 350–359. (Mumbai, 1999) MR 1803462Google Scholar
Wolf, J. A., Spaces of constant curvature (McGraw-Hill Book Co, New York-London-Sydney, 1967). MR 0217740Google Scholar